2. 西南电力设计院,成都 610021
2. Southwest Electric Power Design Institute, Chengdu 610021
导线覆冰是一种受温度、湿度、冷暖空气对流、环流等因素影响的综合物理现象,是液态过冷却水滴撞击导线表面,释放潜热固化的物理过程[1-2]。过重的覆冰对电力设备及其运行造成灾难性影响,带来了严重的经济损失[3]。许多学者对导线覆冰的特征、形成机理和影响因素进行研究[4-6],对建立导线覆冰模型和输电线路的架设及冰冻灾害预防具有重大意义。
国内外现有的导线覆冰模型大致可分为3类:物理概念模型、实验室模型、气象统计模型。物理概念模型主要是运用流体力学、热力学原理对导线覆冰的微观形成过程进行理论分析。Imai[7]提出的物理概念模型较早,认为覆冰强度与空气温度成正比,是湿增长过程,与降水强度无关。Lenhard[8]认为覆冰只与降水量有关,提出了一个非常简单的物理概念模型。Goodwin等[9]假设导线覆冰为干增长过程,在此基础上提出了一个冰厚的概念模型。Makkonen[10]在分析覆冰物理机制的基础上建立了冰柱模型,Maeno等[11]对其进行了改进,Makkonen[12]在总结前人模型的基础上提出了综合新模型。孙才新等[13]对导线覆冰过程中的热平衡进行系统分析后提出了导线覆冰热平衡方程。实验室模型偏重于通过人工改变实验室环境寻找导线覆冰与各种影响因素的关系,建立冰厚与影响要素之间的模型。Chaine[14]在实验室高风速、高液态水含量及小直径液滴情况下建立覆冰模型。刘和云等[15]在实验室模拟的基础上,建立了一种简单覆冰模型,物理意义比较清晰。气象统计模型则是利用气象统计方法对实际气象观测资料和覆冰资料进行统计分析得到覆冰模型。张怀孔[16]以现有的模型为基础,构建了滇东及滇东北地区的导线雨凇覆冰模型。廖玉芳等[17]利用湖南省地面气象观测资料和覆冰资料建立了覆冰厚度估算模型。周绍毅等[18]结合广西90个气象站气象资料,构建了广西输电线路雨凇覆冰模型。
目前国内外关于导线覆冰机理和模型的研究成果虽然很多,但在工程应用上仍有一定限制,例如多数模型中用到诸如液态水含量、液滴的撞击速度之类的因子,由于无法在常规气象观测资料中得到,不能直接应用到工程设计。此外,由于我国的观冰站实际电线积冰观测业务开展较晚,较长的导线覆冰资料序列稀缺,远不能满足输电线路工程设计、建设的需求。因此,利用现有的气象资料和覆冰资料,在分析导线覆冰形成的物理特征的基础上导出常规气象观测要素与电线覆冰厚度的转换关系,不仅对输电线路规划、工程设计具有现实意义,而且能为缺测时段覆冰资料序列的重建提供依据。
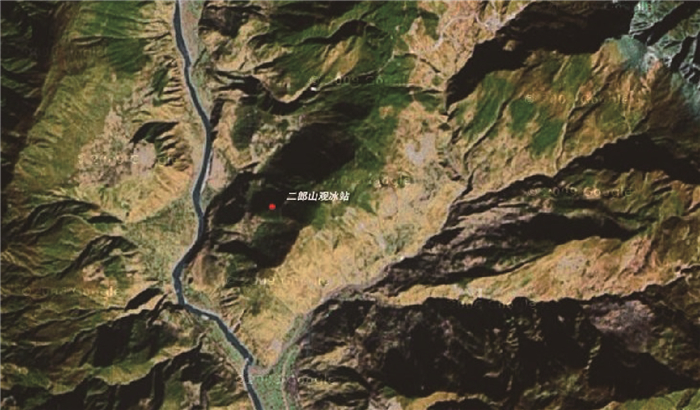
1 资料概况 1.1 观冰站概况本研究所用的覆冰资料是西南电力设计院提供的四川省甘孜州二郎山观冰站观测数据。二郎山观冰站 (29°51′N,102°16′E),海拔为2987 m,地处一个马鞍型垭口 (图 1)。周围山脉主体走向大致为南北走向的起伏山脉,地势较为复杂。
|
|
| 图 1. 二郎山观冰站周边地形 Fig 1. The terrain around ice station of Erlangshan Mountains | |
1.2 资料概况
覆冰资料的观测时段为2006年1月—2009年3月。观测数据取自距地面8 m高导线,线型为LGJ-400,导线直径为27.68 mm。原始覆冰观测要素包括长径、短径及单位长度导线覆冰重量。另外,根据每次观测的长、短径及冰重,计算出每次的覆冰密度和标准冰厚指标。每次覆冰过程均有覆冰开始、发展、保持、消融等时间节点的记录。共获得导线覆冰过程有效样本122个。
本文所用的气象要素资料是2006年1月—2009年3月的气象资料。气象观测站与观冰站相邻。每日观测4次 (02:00,08:00,14:00,20:00,北京时,下同),主要气象要素包括:气温、相对湿度、水汽压、降水量、能见度、风速、风向、云量等。
2 覆冰模型的理论框架根据导线发生覆冰时不同的气象条件,导线覆冰可以分成雾凇覆冰和雨凇覆冰。本文在谭冠日[19]、江祖凡[20]对覆冰增长所作概化的基础上,进一步探讨导线雾凇覆冰和雨凇覆冰的冰厚增长模型。
2.1 雾凇冰厚增长雾凇覆冰是指沿水平气流运动的过冷却液态雾滴在导线上的凝结冰体。在t1时刻,导线覆冰直径为Φ;在t2时刻,导线覆冰直径为Φ+2D,即冰厚增长了D。则该时段实际积冰增加重量 (这里指覆冰增加质量,参见《地面气象观测规范》[21]) 为
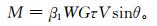
|
(1) |
式 (1) 中,V为水平风速;τ为含过冷却水滴的气流与单位长度导线的接触时段 (τ=t2-t1);G为与导线接触的气流在未受导线的扰动前的截面积;W为单位体积空气中液态水含量;θ为气流与导线的水平交角;WGτVsinθ为τ时段单位长度导线迎风面截获的水量;β1为冻结成冰的比例,即冻结系数 (反映液体水冻结量与水滴捕获量之比,多数文献中近似取值为1,即干增长过程)。所以
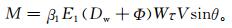
|
(2) |
式 (2) 中,Dw为雾淞覆冰冰厚,E1为捕获系数,是导线接触的气流在未受扰动前的截面积与覆冰导线截面积之比G/(Dw+Φ),反映被干扰的气流中水分的惯性积聚效率。
在时间段τ内,单位长度导线覆冰体积增长量为
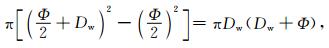
|
(3) |
所以单位长度导线覆冰重量增加量又可以表示为
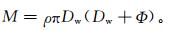
|
(4) |
其中,ρ为覆冰密度。由式 (2) 和式 (4) 可得到雾凇冰厚增长的物理概念模型
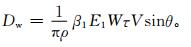
|
(5) |
雨凇覆冰指垂直下落的液态过冷却雨滴在导线上的冻结体,设降水强度为R (单位:mm·h-1),类似可推出,覆冰增长量为
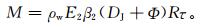
|
(6) |
式 (6) 中,ρw为液态水的密度,这里取ρw=1 g·cm-3;E2为雨凇的捕获系数;β2为雨凇的冻结系数;DJ表示雨凇覆冰冰厚。根据冰厚增加量,则可得到雨凇冰厚增长模型:
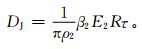
|
(7) |
式 (7) 中,ρ2代表雨凇覆冰的密度。
3 基于能见度指标的覆冰气象模型由覆冰物理概念模型可知,冰重的增长不仅与覆冰导线的直径及冰厚有关,还与诸多要素有关 (式 (2)),因此冰重的公式拟合较复杂。但已知冰厚和覆冰密度时,可由式 (4) 计算得到。所以本文重点讨论覆冰密度和厚度模型的拟合。
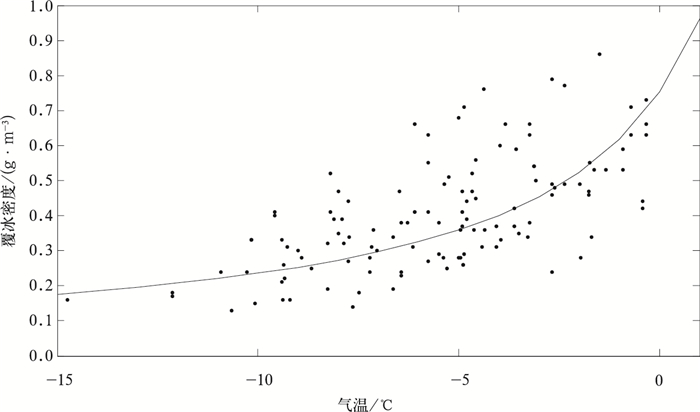
3.1 覆冰密度的拟合覆冰密度与气温、云雾滴谱特征、雨雾滴撞击末速度、导线直径、海拔高度之间存在联系[22]。Macklin[23]根据测定旋转圆柱体覆冰的风洞实验建立了覆冰密度的参数式,认为覆冰密度与温度、雾滴的半径和撞击速度有关。由于在常规气象观测中,上述物理参数无法直接获得。通过对二郎山观冰站实测覆冰密度与对应的气象要素进行相关分析,应用常规气象资料,仅得出覆冰密度与气温 (T) 之间存在显著相关 (图 2)。
|
|
| 图 2. 导线覆冰密度与气温的相关图 Fig 2. The correlation between density of conductor icing and temperature | |
通过对样本进行统计拟合分析,采用下列公式拟合导线覆冰密度 (样本量为122):
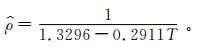
|
(8) |
式 (8) 中,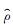
根据式 (5),冰厚增长主要的影响因子是单位体积液态水含量W及其输送量WVsinθ。在常规气象观测中并不包括液态水含量指标,但可以利用常规气象观测值与液态水含量的联系关系来间接估算液态水含量。
云、雾中的液态水粒子的存在可导致消光现象,雾中微物理结构的变化能够影响能见度距离的变化。液滴消光能力的指标称为消光系数,表示液态水粒子对光线削弱的能力,它与液态水含量相关较好,最具代表性的能见度与消光系数参数化方案如下[24]:
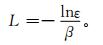
|
(9) |
式 (9) 中,L为能见度;ε为生理视觉阈值,通常都取0.02;β为消光系数,其计算公式为
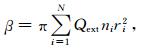
|
(10) |
其中,ni代表半径为ri的粒子数浓度 (单位体积粒子数),Qext是米氏消光系数,与粒子数浓度ni、粒子半径ri及可见光波长有关,而ni和ri基本决定了单位体积液态水的含量W,即β与W之间有密切的相关。
Kunkel[25]发现,消光系数β与液态水含量W的相关系数达到0.95,并得到两者之间的函数关系:

|
(11) |
式 (11) 中,参数a,b由观测资料统计得到,a,b的取值不仅与测量仪器和取样手段相关,而且与环境气溶胶的性质 (雾滴谱) 有关。不同的研究者根据不同的观测资料得到的参数有很大不同 (表 1)。
|
|
表 1 若干能见度与消光系数参数化方案 Table 1 Comparison of different visibility and specific extinction parameterization schemes |
由式 (9)、式 (11) 可得到能见度与液态水含量之间的关系:
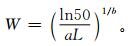
|
(12) |
为在各方案中选择最接近四川山区气候特征的方案,利用文献[29]中成都的部分液态水含量的观测资料,对不同方案反演的液态水含量的效果进行对比 (表 2),结合实际覆冰资料,初步认为Kunkel方案效果较好,选定Kunkel方案进行拟合试验。
|
|
表 2 文献[29]所列成都液态水含量观测值与各能见度反演方案估算值的对比 Table 2 Comparison of observed liquid water (from reference[29]) and estimated visibility by inversion programs |
3.2.2 覆冰冰厚指标的拟合
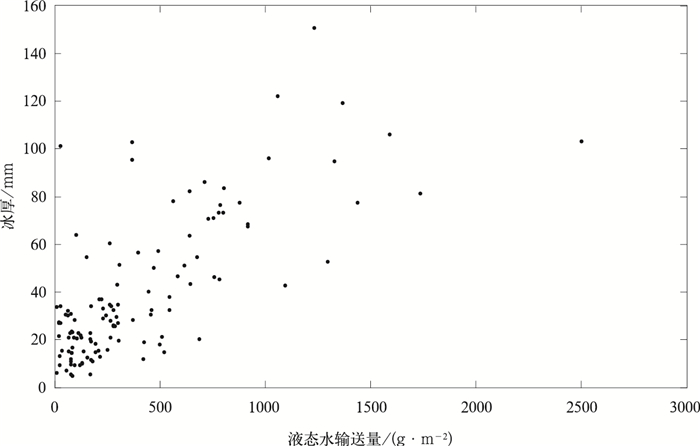
在环境温度满足的条件下,覆冰强度的物质基础是液态水输送量,液态水含量由式 (12) 反演推算估计。以覆冰过程的液态水输送量WVsinθ·τ为指标,从图 3可以看出,冰厚D增长与液态水输送量存在良好的相关。
|
|
| 图 3. 导线冰厚与液态水输送量的相关散点图 Fig 3. The correlation scatter diagram between icing thickness and liquid water transmission | |
指标WVsinθ·τ是水平方向的液态水输送量,在覆冰过程中常常伴有降水过程,为垂直向的液态水,在冰厚模型的拟合过程中需综合考虑降水的影响。
将冰厚D分解为水平雾滴运动形成的Dw与降水过程形成的DJ,即
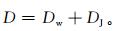
|
(13) |
对降水形成的雨凇覆冰,密度ρ2近似取0.9 g·cm-3;考虑雨滴较雾滴体积大,惯性大,再考虑雨滴截面对应覆冰翼型形状的长径等因素,取E2≈1,并假定降落到导线的雨滴全部冻结,即β2≈1,由式 (7),得
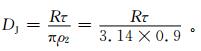
|
(14) |
定义覆冰过程效率指标 (反映单位液态水输送条件下覆冰增长的程度) 为

|
(15) |
由式 (15) 可以看出,覆冰过程效率指标Y反映了导线覆冰的冻结效率和捕获效率。从物理意义上分析,影响冻结和捕获效率的主要气象因子是气温和风速。但对实测资料的相关分析,Y与气温的相关不显著,说明多数情况下,覆冰呈干增长过程,冻结系数近于1。
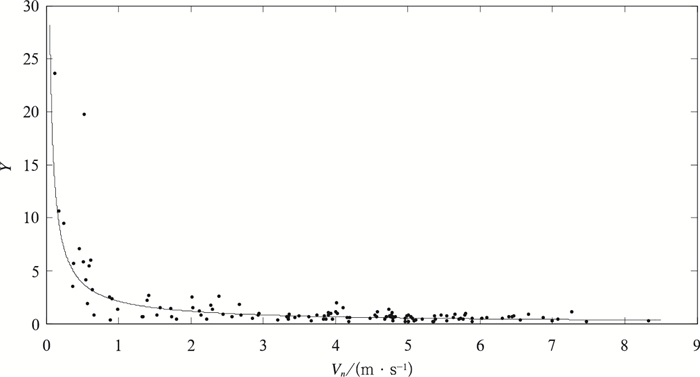
由Y与风速的相关散布 (图 4) 可以看出,样本点的分布近似为指数分布,通过对样本进行回归分析,得到导线覆冰过程效率指标的拟合公式 (样本量n为122),
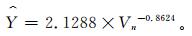
|
(16) |
|
|
| 图 4. 导线覆冰过程效率指标Y与Vn的相关散布图 Fig 4. The correlation scatter diagram between process efficiency of conductor icing and wind speed | |
式 (16) 中,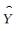
将式 (5)、式 (15) 组合可得
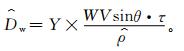
|
(17) |
导线覆冰气象综合模型公式:
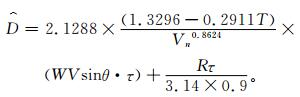
|
(18) |
为检验覆冰气象因子参数化数学模型的准确程度,将覆冰拟合冰厚值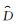
|
|
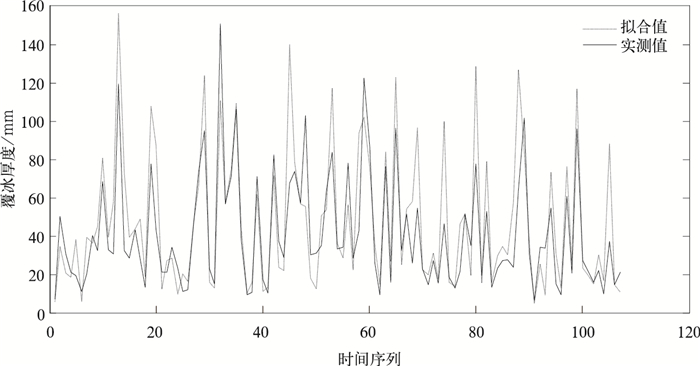
| 图 5. 覆冰过程冰厚实测值与拟合值的时序比较 Fig 5. The comparison of observed icing process thickness and fitted one | |
|
|
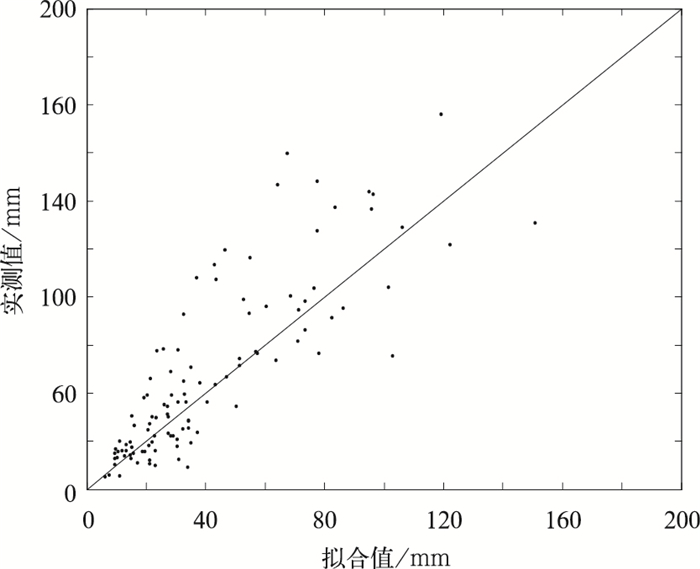
| 图 6. 冰厚实测值与拟合值对比 Fig 6. The comparison of observed icing thickness and fitted one | |
从拟合结果来看,覆冰气象模型总体上能反映实际的观测结果, 尤其对变化趋势体现得很好。另外,作为定量的误差指标,计算了覆冰拟合冰厚值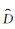
能见度与液态水反演方案的客观性是冰厚拟合准确性的关键之一,对表 2所列的各能见度反演方案全部进行了试验,拟合效果最好的是Kunkel方案。例如Pinnick方案,其效率指标Y的拟合相关比为0.6601,拟合值与实测值的相关系数为0.6760,均方根误差为31.81 mm。从对比结果看,基于Kunkel能见度反演方案建立的覆冰模型的拟合效果要优于其他3个能见度反演方案。
从图 5、图 6看到,对部分覆冰冰厚特别是较大值的冰厚模拟效果还不够理想。分析其原因,除随机性误差以外,更多的是由于现有覆冰的观测技术缺陷及模型设计不足带来的误差。由于对覆冰增长有重要影响的雾滴谱在本研究中没有实测资料;模型中均匀柱体覆冰假设与实际情况下导线的翼型不均匀覆冰的差异也会对结果带来误差,这些因素都会对模型的拟合精度带来影响。另外,由于液态水W与消光系数β的经验公式 (11) 及其参数a,b均引用国外的研究结果,不一定适合我国的气候特点。总结符合我国气候特征的经验公式及其参数,将有利于模型准确率的提高。
4 结论本研究通过分析四川省二郎山观冰站2006年1月—2009年3月的覆冰资料和同期气象资料,得到了如下结果:
1) 通过对实测覆冰资料与同期气象资料的分析,发现覆冰密度仅与气温存在显著相关,进而建立了以气温为参数的导线覆冰密度模型。拟合的覆冰密度公式可以较好地反映实际覆冰密度。
2) 引用能见度L与消光系数β的参数化方案以及消光系数与液态水含量W的相关关系,得到了能见度与液态水含量的函数关系式,采用间接估算的方式来表示空气中的液态含水量。
3) 根据拟合的覆冰过程密度模型及各气象资料建立了覆冰过程效率模型,进而得到了气象因子参数化的覆冰冰厚模型。建立的覆冰冰厚模型的拟合值与实测值之间的相关系数达到0.8340,均方根误差为28.61 mm,拟合值基本反映了实际的覆冰发生情况。
| [1] | 甘凤林, 马涛, 黄金花. 导线覆冰对架空输电线路结构的影响. 华北电力技术, 2008, 8: 5–7. DOI:10.3969/j.issn.1003-9171.2008.02.002 |
| [2] | 张岩, 叱志祥, 张国彦. 达坂山导线覆冰与气象条件的关系. 青海电力, 2005, 24, (1): 33–36. |
| [3] | 殷水清, 赵珊珊, 王遵亚, 等. 全国电线结冰厚度分布及等级预报模型. 应用气象学报, 2009, 20, (6): 722–728. DOI:10.11898/1001-7313.20090610 |
| [4] | 吴素良, 范建勋, 姜创业, 等. 兰州至关中电线积冰与导线线径及高度关系. 应用气象学报, 2010, 21, (1): 63–69. DOI:10.11898/1001-7313.20100108 |
| [5] | 吴素良, 蔡新玲, 何晓媛, 等. 陕西省电线积冰特征. 应用气象学报, 2009, 20, (2): 247–251. DOI:10.11898/1001-7313.20090215 |
| [6] | 张国庆, 张加昆, 祁栋林, 等. 青海东部电线积冰的初步观测分析. 应用气象学报, 2006, 17, (4): 508–510. DOI:10.11898/1001-7313.20060419 |
| [7] | Imai I. Studies on ice accretion. Researches on Snow and Ice, 1953, 3, (1): 35–44. |
| [8] | Lenhard R W. An indirect method for estimating the weight of glaze on wires. Bull Amer Meteor Soc, 1955, 36, (3): 1–5. |
| [9] | Goodwin E J, Mozer J D, Di Gioia A M. Predicting Ice and Snow Loads for Transmission Lines. Proceedings, First IWAIS, 1983:267-273. |
| [10] | Makkonen L. A model of icicle growth. J Glaciol, 1988, 34: 64–70. DOI:10.1017/S0022143000009072 |
| [11] | Maeno N, Makkonen L, Nishimura K, et al. Growth rates of icicles. Journal of Glaciology, 1994, 1, (40): 319–326. |
| [12] | Makkonen Lasse. Modeling power line icing in freezing precipitation. Atmospheric Research, 1998, 46: 131–142. DOI:10.1016/S0169-8095(97)00056-2 |
| [13] | 孙才新, 蒋兴良, 熊启新, 等. 导线覆冰及其干湿增长临界条件分析. 中国电机工程学报, 2003, 23, (3): 141–145. |
| [14] | Chaine P M, Casfonguay G. New Approach to Radial Ice Thickness Concept Applied to Bundle-like Conductors//Industrial Meteorology: Study 4. Toronto: AES, Environment Canada, 1974. |
| [15] | 刘和云, 周迪, 付俊萍, 等. 导线雨淞覆冰预测简单模型的研究. 中国电机工程学报, 2001, 21, (4): 44–47. |
| [16] | 张怀孔. 滇东及滇东北地区电线覆冰模型研究. 电力勘测设计, 2007, 4: 40–42. DOI:10.3969/j.issn.1671-9913.2007.03.011 |
| [17] | 廖玉芳, 段丽洁. 湖南电线覆冰厚度估算模型研究. 大气科学学报, 2010, 33, (4): 395–400. |
| [18] | 周绍毅, 苏志, 秦军, 等. 基于覆冰模型和GIS的广西输电线路覆冰区划分研究. 广西电力, 2010, 33, (2): 11–13. |
| [19] | 谭冠日. 电线积冰若干小气候特征的讨论. 气象学报, 1982, 40, (1): 13–23. DOI:10.11676/qxxb1982.002 |
| [20] | 江祖凡. 电线积冰增长速度的研究. 科学通报, 1983, 15: 928–931. |
| [21] | 中国气象局. 地面气象观测规范. 北京: 气象出版社, 2003. |
| [22] | 罗宁, 文继芬, 赵彩, 等. 导线积冰的云雾特征观测研究. 应用气象学报, 2008, 19, (1): 91–95. DOI:10.11898/1001-7313.20080114 |
| [23] | Macklin W C. The density of structure of ice formed by accretion. Quarterly Journal of the Royal Meteorological Society, 1962, 88: 30–35. DOI:10.1002/(ISSN)1477-870X |
| [24] | 林云, 孙向明, 张小丽, 等. 深圳市大气能见度与细粒子浓度统计模型. 应用气象学报, 2009, 20, (2): 252–256. DOI:10.11898/1001-7313.20090216 |
| [25] | Kunkel B A. Parameterization of droplet terminal velocity and extinction coefficient in fog models. J Climate Apply Meteor, 1984, 23: 34–41. DOI:10.1175/1520-0450(1984)023<0034:PODTVA>2.0.CO;2 |
| [26] | Eldridge R G. The relationship between visibility and liquid water content in fog. Atmos Sci, 1971, 28: 1183–1186. DOI:10.1175/1520-0469(1971)028<1183:TRBVAL>2.0.CO;2 |
| [27] | Pinnick R G, Hoihjelle D L, Fernandez G, et al. Vertical structure in atmospheric fog and haze and its effects on visible and infrared extinction. Atmos Sci, 1978, 35: 2020–2032. DOI:10.1175/1520-0469(1978)035<2020:VSIAFA>2.0.CO;2 |
| [28] | Tomasi C, Tampieri F. Features of the proportionality coefficient in the relationship between visibility and liquid water content in haze and fog. Atmosphere, 1976, 14: 61–76. |
| [29] | 乐时晓. 能见度与液态水含量的实验. 成都电讯工程学院学报, 1984, (增刊): 8–11. |
 2012, 23 (6): 755-762
2012, 23 (6): 755-762



