2. 武汉中心气象台,武汉 430074;
3. 湖北省防雷中心,武汉 430074
2. Wuhan Central Meteorological Observatory, Wuhan 430074;
3. Hubei Lightning Protection Center, Wuhan 430074
双线偏振雷达通过交替发射或者同时发射水平和垂直偏振波,并接收两个偏振方向回波信号的方法,可以探测到降水系统的回波强度ZH、差分反射率因子ZDR、差分传播相移ΦDP、差分传播相移率KDP以及零滞后互相关系数ρHV(0) 等参数,这些参数直接反映了降水系统的粒子相态、滴谱分布 (DSD) 等微物理结构的变化规律,从而明显提高雷达估测降水和进行降水粒子相态识别的能力[1-2]。
定义ΦDP=ΦH-ΦV,其中,ΦH, ΦV分别为传播路径上给定点的水平、垂直偏振波的相位,ΦDP表示水平、垂直偏振波在传播一定距离后散射回来的信号相位差,但它不包括散射过程本身引起的相位变化。在一个充满水平取向 (降水粒子的水平轴长于垂直轴) 水凝物粒子 (例如水和冰晶) 的分辨体积中,水平极化波在单位长度上有更大的相移,传输速度较垂直极化波慢;而垂直取向 (降水粒子的垂直轴长于水平轴) 的水凝物粒子相反。
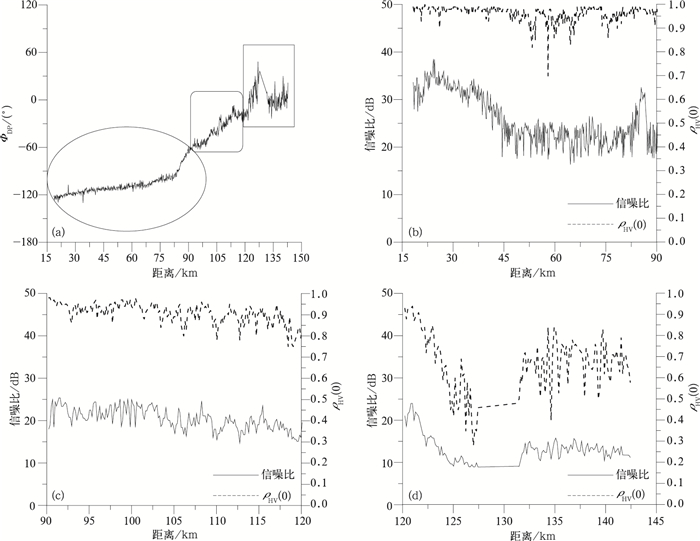
KDP是由降水粒子前向散射的相位差异造成的,它表示粒子对雷达波传播速度或相位的影响。对于给定的有限距离,常用下式进行估计:
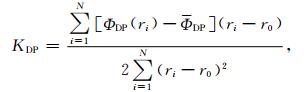
|
(1) |

|
(2) |
其中,ri为第i个库与雷达之间的径向距离;ΦDP为N个库的ΦDP平均值。由于KDP具有不受雷达标定误差、雨区衰减等因素的影响,与降水强度几乎呈线性关系且对雨滴谱变化不敏感等特点,因此被广泛应用于雷达定量估测降水及衰减订正[3]。
国内目前在ΦDP资料处理方面开展的工作还不多,对ΦDP资料的质量控制仅局限于一般的预处理,包括距离平滑、滑动平均和中值滤波等。曹俊武[4]对双线偏振雷达资料平滑方法进行了相关分析。何宇翔等[5]根据差分传播相移的特点引入了卡尔曼滤波方法。国外则大都采用迭代滤波的方法来处理。Hubbert等[6]利用有限冲激响应FIR (finite impulse response) 和无限冲激响应IIR (infinite impulse response) 低通滤波器对ΦDP数据进行了处理。Hubbert等[7]随后改进了该方法,提出了一种迭代滤波的方法。该方法比简单的低通滤波器方法具有更广泛的应用范围,使用效果不错,但一般数据处理时间较长。
目前,对ΦDP资料的处理和质量控制主要集中在滤波方法的研究方面,本文通过对大量ΦDP资料进行特征分析,构建出一套系统的ΦDP资料分类处理方法。该方法能根据实际情况将ΦDP资料分为非气象信号、较好、较差和差气象信号4类,并根据不同的应用需要对非气象信号进行不同处理,对较好气象信号不处理,而对较差和差的气象信号分别进行订正和剔除处理。该方法对ΦDP资料进行了较为全面的处理,在最大程度上保留气象信息的同时,也保证了ΦDP资料的整体质量,其估算的KDP数据的分布也更加合理。
1 双线偏振雷达ΦDP资料特征 1.1 地物杂波的ΦDP资料特征双线偏振雷达探测到的非气象因子主要包括地物、飞机、飞鸟、昆虫、海浪等。由于地物杂波最常见且造成的影响最大,因此对其进行重点分析。地物回波主要出现在低层,径向速度和速度谱宽都很小,没有明显的移动迹象,其偏振特性表现为地物杂波的ZDR往往会偏离气象回波正常的取值范围 (-2~6 dB),一般为明显偏低,偶尔也会明显偏大;地物杂波的KDP也会出现类似现象,较正常的降水回波有较大波动;ρHV(0) 较正常气象回波取值范围 (一般大于0.9) 偏小很多,大部分地物杂波的ρHV(0) 分布在0.4~0.7范围内[8]。对大量ΦDP资料进行观察分析后发现,ΦDP资料易受地物影响,主要表现为对应距离库的ΦDP出现大的异常波动。
图 1a、图 1c为CPDRW 0.5°仰角下ZH的PPI图,图 1b、图 1d则分别对应图 1a、图 1c中红线标示径向ΦDP和径向速度Vr的距离廓线图。从对应Vr的PPI图 (图略) 上可以发现,图 1a中大面积回波的Vr均为零,而图 1c只有雷达近距离处存在零星的零速度回波,且随着雷达仰角的抬升,零速度回波都逐渐减少,直至消失。从Vr距离廓线也可以分辨出明显的地物特征。对连续多个时次的雷达资料进行观察后发现,上述区域的回波位置也都没有明显移动,因此可判断图 1a存在大面积的地物,而图 1c存在小范围的零星地物。除此之外,由图 1还可以清楚地看到,无论雷达电磁波经过大面积的地物区还是小范围的零星地物,对应的ΦDP资料都会出现明显异于正常气象目标的波动。
|
|
| 图 1. CPDRW大面积地物ZH的PPI图 (a) 及其红线标示径向ΦDP距离廓线图 (b) 与零星地物ZH的PPI图 (c) 及其红线标示径向ΦDP距离廓线图 (d)(雷达仰角为0.5°; 距离圈间隔为50 km; 径向射线间隔为30°) Fig 1. The PPI of reflectivity CPDRW for large area ground (a) with its range profiles of ΦDP(b) denoted by red solid line in Fig. 1a and sporadic ground (c) with its range profiles of ΦDP (d) denoted by red solid lines in plot Fig. 1c, respectively (the elevation is 0.5°; the distance between adjacent circles is 50 km; the degree between adjacent radical lines is 30°) | |
1.2 气象回波的ΦDP资料特征
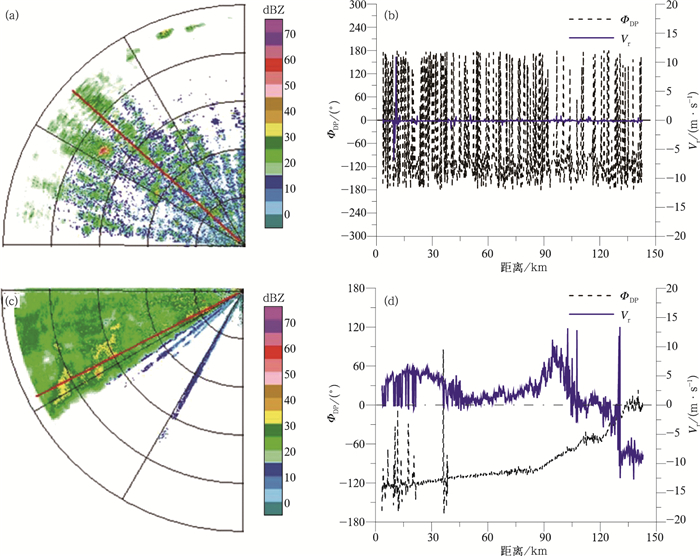
气象目标的ΦDP是一个积分效应量,即使是在大雨情况下其增量也小于8°~10°·km-1(根据雷达频率的不同而不同),而ΦDP的径向廓线是距离的平滑函数,其变化相对较慢,因此,从理论上讲,气象回波的ΦDP径向廓线整体上呈现出随距离增大而增加的变化趋势[7, 9]。其中,对于强度相对较弱且分布均匀的降水回波 (如大面积层状云降水),ΦDP一般随距离缓慢递增。当雷达电磁波穿过一块较强的降水回波 (如对流单体) 时,ΦDP会在该区域出现明显增大。但在实际探测中,由于地物等非气象目标的干扰、大气环境场的扰动、气象目标自身的涨落,以及雷达系统存在的各种噪声与误差,均使ΦDP资料质量受到影响,存在抖动起伏现象。尤其是弱回波区,其ΦDP资料一般较差[5, 10]。在对大量资料进行分析后发现,ΦDP资料对信噪比和ρHV(0) 的变化很敏感,尤其是后者。
图 2a为典型气象回波的ΦDP距离廓线图,而图 2b、图 2c、图 2d分别对应图 2a中椭圆、圆角矩形和矩形3个区域资料的信噪比和ρHV(0) 距离廓线图。
|
|
| 图 2. ΦDP、信噪比与ρHV(0) 距离廓线图 (图 2b、图 2c、图 2d分别对应图 2a中椭圆、圆角矩形、矩形3个区域) Fig 2. Range profiles of ΦDP, SNR and ρHV(0) (Fig. 2b, Fig. 2c, Fig. 2d corresponding to the elliptic, rounded rectangle, rectangular areas in Fig. 2a, respectively) | |
由图 2a可以看到,3个区域的ΦDP资料都存在波动起伏现象,但表现出的波动特点却有所不同。椭圆框中的ΦDP资料波动较小,其整体变化趋势明显且符合理论预期,毛刺现象也可以通过滤波处理加以消除,因此为较好资料且可直接用于KDP的估算;随着探测距离的增大,信噪比开始降低,圆角矩形框中的ΦDP资料抖动开始加剧,数据连续性也开始变差,但对这类资料加以订正仍能用其估算KDP,因此为较差资料;随着探测距离的进一步增大,信噪比变得更低,普遍低于20 dB,信号受噪声影响严重使得测量值存在较大偏差,矩形框中的ΦDP资料不仅抖动剧烈,变化趋势也较难辨识,甚至还出现了与理论相违背的负增长现象,这样的数据即使进行滤波处理,仍会导致估算的KDP产生较大偏差,甚至出现正负极值,因此为差资料。从图 2b、图 2c、图 2d还可以发现:较好ΦDP资料除个别距离库以外,大部分的ρHV(0) 都在0.9以上,信噪比也都大于20 dB,且大部分都大于25 dB;较差ΦDP资料的ρHV(0) 低于0.9的明显增多,信噪比在20~25 dB范围内;差ΦDP资料的ρHV(0) 则普遍低于0.8,有些甚至小于0.5,而信噪比也同样偏低,基本小于15 dB。
2 双线偏振雷达ΦDP资料分类处理方法 2.1 处理方法简介第1步,由于ρHV(0) 易受噪声的影响,尤其是在信号较弱或出现小雨、降雪的情况下[8, 11],因此在对ΦDP资料进行处理前应先对ρHV(0) 进行噪声订正 (订正公式见文献[11])。
第2步,确定ΦDP的有效起始距离库和初始相位。小的ΦDP方差和大的ρHV(0) 常被用来探测气象回波[9],因此将连续10个距离库ΦDP无异常波动且ρHV(0)>0.9的起始距离库作为当前径向的有效起始距离库,并将这10个库的ΦDP平均值作为该径向的初始相位。
第3步,设置ΦDP阈值并结合ZH和Vr对径向ΦDP异常波动进行滑动检测。当用于地物识别时将其保留,而进行降水估测、衰减订正等定量应用时则将其剔除。
第4步,利用信噪比和ρHV(0) 将气象回波信号分为较好、较差和差3类。对于较好资料,直接对其进行后续处理;对于较差资料,由于信噪比的降低导致其起伏变大,但这些均为无偏估计[5],其中仍包含较多有用的气象信息,为了尽可能将其保留,且保证资料的连续性,建议使用相邻距离库的ΦDP距离加权值或前面若干库的ΦDP平均值对其进行订正;而对于差资料,由于信号太弱,ρHV(0) 太小导致这部分资料不可信,为了不影响ΦDP及其估算的KDP资料的整体质量,将其剔除。
第5步,估算KDP。其中,距离库数N根据ZH进行如下取值[9]:
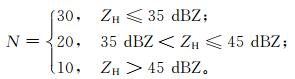
|
(3) |
上述取值方法可以减少因观测资料扰动而产生的误差,对于强的回波区,采用较短的拟合距离可以减少周围弱回波的影响,从而保持强回波区的特征[9-10]。
2.2 阈值参数设置Kostinski[12]将ΦDP的概率密度谱与其对应的波动强度进行对比分析后发现,随着水平与垂直偏振回波的相关性变差,即ρHV(0) 减小,其概率密度函数会展宽,这标志着ΦDP的波动开始加剧。低信噪比和小ρHV(0) 往往会导致大的相位波动[9]。由CPDRW雷达资料的信噪比与ΔΦDP和信噪比与ρHV(0) 散点分布图 (图略) 可知,当信噪比小于20 dB时,ΔΦDP(相邻两库的ΦDP差值) 明显发散,这表明ΦDP的波动加剧;而信噪比又是影响ρHV(0) 质量的重要因素[11],当信噪比小于20 dB时,ρHV(0) 基本低于0.9,且大部分集中在0.7以下,并随着信噪比降低而减小;而当信噪比大于25 dB时,ρHV(0) 逐渐增大,并迅速向1.0靠拢。因此认为信噪比小于20 dB或ρHV(0) 小于0.7的数据不可信,为差资料,而信噪比大于25 dB且ρHV(0) 大于0.9的为较好资料,其他则为较差资料。经过大量的资料分析,将ΦDP异常波动阈值设定为15°。
3 个例分析为了检验ΦDP分类处理方法的实际效果,利用CPDRW的外场观测数据进行验证。该雷达采用双发双收模式,波长为5.5 cm,峰值功率250 kW,脉冲重复频率300~1200 Hz,脉冲宽度为0.5, 1 μs,距离库长为75,150 m,探测距离为75,150 km。
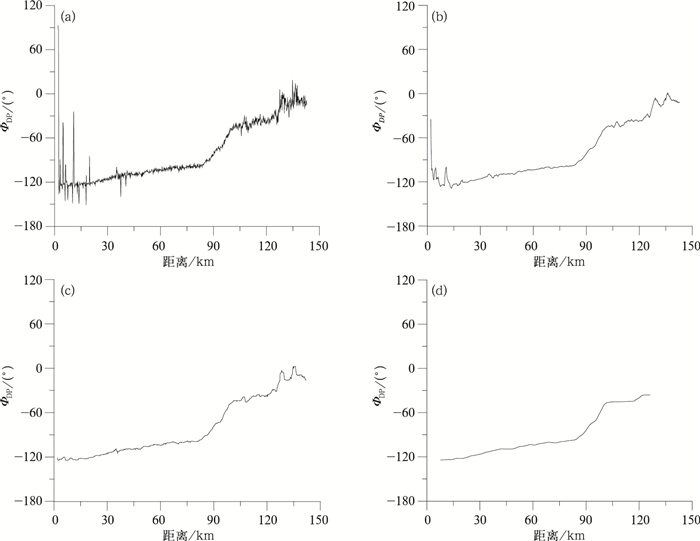
图 3为2008年6月6日09:44(北京时,下同) CPDRW 1.5°仰角,245.8°方位角的ΦDP原始资料及分别经过十三点 (约2 km,下同) 滑动平均、十三点中值滤波和分类处理后的ΦDP距离廓线图。
|
|
| 图 3. 2008年6月6日09:44 CPDRW 1.5°仰角,245.8°方位角ΦDP距离廓线 (a) 原始资料,(b) 十三点滑动平均,(c) 十三点中值滤波,(d) 分类处理 Fig 3. Comparison of range profiles of CPDRW ΦDP at 0944 BT 6 June 2008 with the elevation of 1.5°, azimuth of 245.8° (a) raw data, (b)13-point moving average, (c)13-point median filtering, (d) classification processing | |
由原始ΦDP资料 (图 3a) 不难发现,该径向数据连续性较好,整体的变化趋势与理论分析也完全一致。其中,前82 km的ΦDP呈现出缓慢递增的变化趋势,其ZH均匀分布在20~25 dBZ范围内 (图略);而在82~100 km之间电磁波刚好穿过一块较强回波 (ZH>30 dBZ),ΦDP也出现了明显的大幅递增。除此之外,整个径向还存在毛刺现象及一些大的波动 (甚至是数值尖峰)。近距离处受零星地物的干扰产生了大幅度的异常波动。远距离处则由于信号较弱,ΦDP资料的波动加剧。十三点滑动平均 (图 3b) 和十三点中值滤波 (图 3c) 对ΦDP数据的脉动都起到了一定的平滑作用,但滑动平均对地物引起ΦDP异常波动的处理还不够,而中值滤波在这方面的处理效果虽好于滑动平均,但两者对远距离处质量差的ΦDP资料都显得无能为力,依旧保留了其整体的波动趋势。分类处理 (图 3d) 不仅很好地抑制了ΦDP数据的脉动,其整体的变化趋势也得到了保留。与此同时,原始数据存在的非气象回波干扰以及那些无法被很好处理的质量差的数据也被剔除。由此可见,分类处理方法较之常规的滑动平均和中值滤波方法具有更为明显的处理效果。
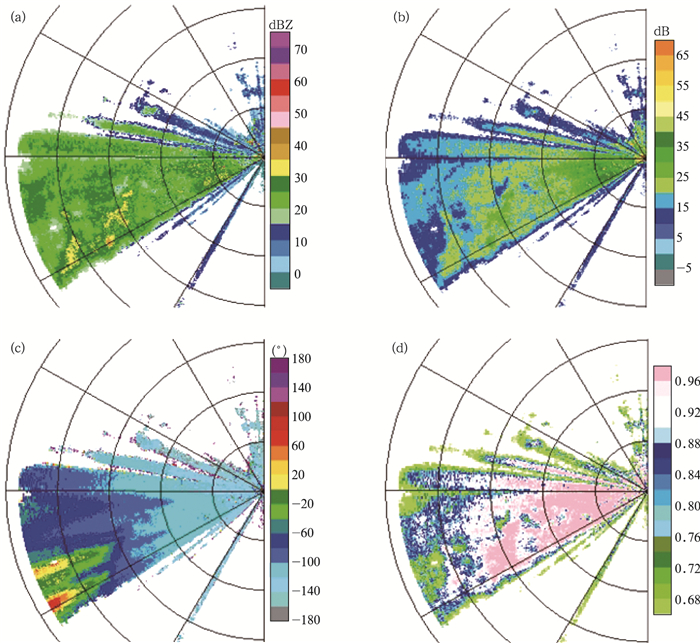
图 4为2008年6月6日09:44 CPDRW 0.5°仰角原始资料ZH信噪比、ΦDP及ρHV(0) 的PPI图 (方位角范围为180°~360°,雷达位于半圆的中心位置,下同)。由图 4可以看到,雷达回波边缘及雷达远端的信号较弱,信噪比大都在20 dB以下,ρHV(0) 也普遍低于0.9,有些甚至低于0.7。而这些区域的ΦDP也以散点分布为主,有些地方甚至出现了颜色断层现象 (即ΦDP出现负增长),这明显与ΦDP的理论特性相违背。
|
|
| 图 4. 2008年6月6日09:44 CPDRW 0.5°仰角PPI图 (a)ZH,(b) 信噪比,(c)ΦDP,(d)ρHV(0) Fig 4. The PPI CPDRW for ZH(a), SNR (b), ΦDP (c), ρHV(0)(d) at 0944 BT 6 June 2008 with the elevation of 0.5° | |
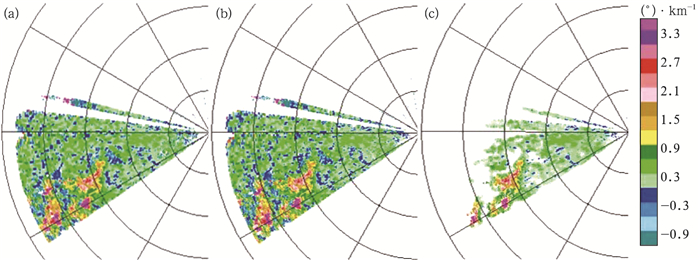
图 5对ΦDP经3种方法处理后估算的KDP进行了对比。其中,ΦDP经十三点滑动平均 (图 5a) 和十三点中值滤波 (图 5b) 处理后估算的KDP数据整体的层次性较好,与ZH(图 4a) 也都具有较好的对应关系。但雷达回波边缘及雷达远端的KDP数据主要呈散点分布,变化较散乱,无法识别出其具体的分布特征,而且数据中还充斥了许多KDP的负值点,使其显得更加凌乱,甚至出现了正负极值。这些KDP数据较差的地方也正是信噪比 (图 4b) 偏低、ρHV(0)(图 4d) 偏小的弱回波区。如果用这样的KDP数据进行降水估测或降水粒子相态识别势必会产生很大误差,而产生这些KDP负值和错误极值的原因正是由于两种常规处理方法将质量差的ΦDP数据一并处理导致的。常规处理方法只能滤除ΦDP资料中的脉动和毛刺,处理后的气象信号中依然包含了这些异常波动信息,因此,由这样的ΦDP资料估算的KDP资料势必会出现很多负值甚至异常极值。分类处理方法则对这部分异常波动数据进行了剔除,从而排除了其对估算的KDP的影响。经过分类处理后 (图 5c),由于剔除了一些波动异常点及难以处理的质量差的数据点,KDP回波面积明显减小,但强回波区域仍得到了保留。除了KDP异常点基本得到剔除以外,KDP负值点也明显减少。这也充分说明了该方法能在最大程度上保留气象信息的同时,保证ΦDP资料的整体质量。
|
|
| 图 5. 2008年6月6日09:44 CPDRW 0.5°仰角ΦDP经不同方法处理后估算的KDPPPI图 (a) 十三点滑动平均,(b) 十三点中值滤波,(c) 分类处理 Fig 5. The PPI CPDRW of KDP for different ΦDP processing methods at 0944 BT 6 June 2008 with the elevation of 0.5° (a)13-point moving average, (b)13-point median filtering, (c) classification processing | |
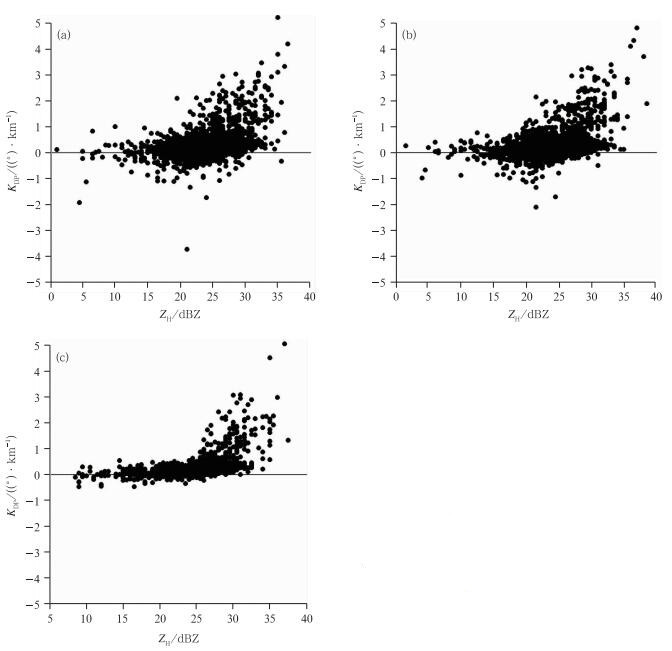
图 6即为ZH与ΦDP分别经过3种不同方法处理后估算的KDP的散点分布图。
|
|
| 图 6. 2008年6月6日09:44 CPDRW 0.5°仰角ZH与ΦDP经不同方法处理后估算的KDP的散点分布 (a) 十三点滑动平均,(b) 十三点中值滤波,(c) 分类处理 Fig 6. The scatter plot of ZH, KDP in PPI CPDRW with the elevation of 0.5° at 0944 BT 6 June 2008 for different ΦDP processing methods (a)13-point moving average, (b)13-point median filtering, (c) classification processin | |
一般而言,弱降水的降水粒子接近球形,其KDP比较凌乱,呈零值附近的无规则分布。而大的液态降水粒子,由于自身重力及表面张力作用一般呈扁平型 (长轴在水平轴),其KDP值为较大的正值。由图 6可以看到,KDP有随ZH增大而增大的变化趋势,但图 6a、图 6b中却存在大量的KDP负值点,甚至有KDP<-2°·km-1的极小值,这与降水粒子KDP一般大于零的理论相违背。而在图 6c中,ΦDP经过分类处理后估算的KDP值基本都位于零值线以上,ZH和KDP之间也有较明显的对应关系,这种偏振参数的变化特性同RyZHkov等[13]的研究成果相一致。这说明了分类处理方法对ΦDP的处理及其估算的KDP对降水粒子的特性反映合理有效[14-15],比较符合客观实际情况,可以进行后续分析。
2009年9月15日在广东珠海出现了一次混合性降水过程,由于分析方法与之前个例相同,在此只做简要分析。图 7为9月15日01:27 CPDRW 0.5°仰角原始资料ZH、信噪比、ΦDP及ρHV(0) 的PPI图。从图 7可以发现,该个例整体的ZH和信噪比均大于之前的个例,但雷达回波边缘及雷达远端的信号仍然相对较弱,信噪比会降到25 dB以下,有些还会低于20 dB;其对应的ρHV(0) 也普遍小于0.9,有些甚至小于0.7。与此同时,对应区域的ΦDP也以散点分布为主,颜色分布不均匀且连续性较差,会有颜色断层现象出现。

|
|
| 图 7. 2009年9月15日01:27 CPDRW 0.5°仰角PPI图 (a)ZH,(b) 信噪比,(c)ΦDP,(d)ρHV(0) Fig 7. The PPI CPDRW for ZH(a), SNR (b), ΦDP(c), ρHV(0)(d) at 0127 BT 15 September 2009 with the elevation of 0.5° | |
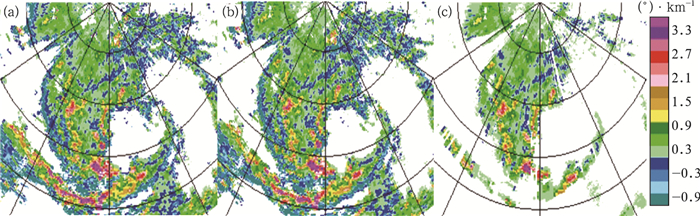
将ΦDP经3种不同方法处理后估算的KDP(图 8) 进行对比后看到,经两种常规方法处理后,由差ΦDP资料估算的KDP分布很散乱,且存在较多的负值点,甚至出现了许多正负极值。而分类处理方法在保留大量有用气象信息 (包括强回波信息) 的同时,有效地剔除了差的KDP数据,从而保证了数据的整体质量。上述结论与之前个例的分析结论也是一致的。
|
|
| 图 8. 2009年9月15日01:27 CPDRW 0.5°仰角ΦDP经不同方法处理后估算的KDPPPI图 (a) 十三点滑动平均,(b) 十三点中值滤波,(c) 分类处理 Fig 8. The PPI CPDRW of KDP for different ΦDP processing methods at 0127 BT 15 September 2009 with the elevation of 0.5° (a)13-point moving average, (b)13-point median filtering, (c) classification processing | |
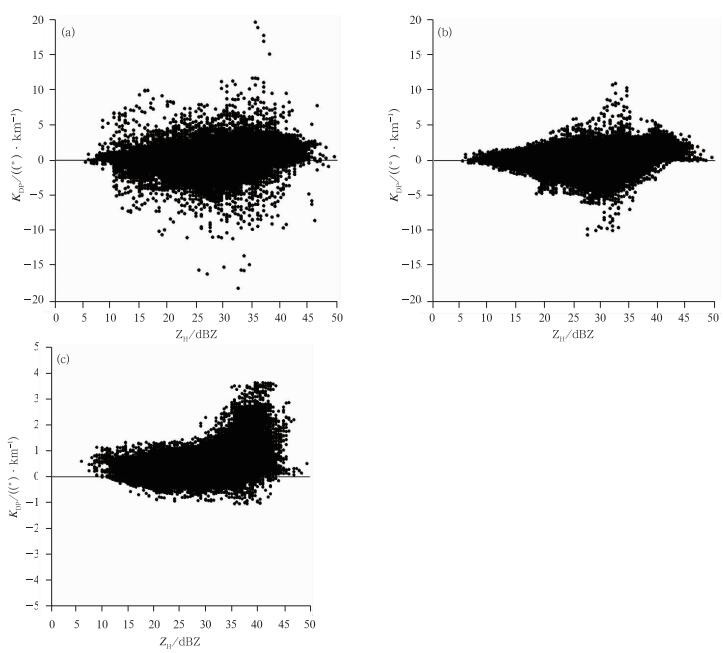
图 9为ZH与ΦDP经3种不同方法处理后估算的KDP的散点分布图。对比可知,ΦDP经两种常规处理方法处理后估算的KDP(图 9a、图 9b) 不仅存在较多负值点,更有|KDP|>10°·km-1的异常极值出现,这些都与气象目标的偏振特性不相符[16-18]。分类处理方法 (图 9c) 在剔除KDP异常极值的基础上明显减少了KDP的负值点,KDP随ZH的增大而递增的变化趋势也更加明显,这些都与RyZHkov等[13]的研究成果相一致。用同一方法对其他过程资料的分析也可以得到相同的结论。
|
|
| 图 9. 2009年9月15日01:27 CPDRW 0.5°仰角ZH与ΦDP经不同方法处理后估算的KDP的散点分布 (a) 十三点滑动平均,(b) 十三点中值滤波,(c) 分类处理 Fig 9. The scatter plot of ZH, KDP in PPI CPDRW with the elevation of 0.5°at 0127 BT 15 September 2009 for different ΦDP processing methods (a)13-point moving average, (b)13-point median filtering, (c) classification processing | |
4 小结
本文以CPDRW资料为例,分析了ΦDP的资料特征,提出了对ΦDP资料进行分类处理的方法,并利用该雷达外场试验时获取的探测数据对该方法进行了验证,得到如下结论:
1) ΦDP易受地物干扰而存在明显区别于气象信号的异常波动现象,在进行定量应用时需要将其剔除,可通过设置一定的波动阈值对其进行识别。经过大量资料的检验,CPDRW ΦDP资料中的异常波动能够被较好地识别。
2) ΦDP对信噪比及ρHV(0) 的变化比较敏感,尤其是后者。为了在保留气象信息的同时最大程度地提取出好的ΦDP资料以估算出高质量的KDP资料,根据信噪比和ρHV(0) 将ΦDP资料分为较好、较差和差3类,并对其进行不同处理。
天气雷达信号自身的涨落以及降水系统的演变和移动等原因会造成雷达测量到的参数产生较大脉动,这种脉动对偏振参数的影响更为明显。就目前而言,要完全消除这种脉动还很难,国内外也都没有很好的方法,这也是在利用偏振参数时要特别注意的地方。
另外,在进行ΦDP资料分类处理时需要注意,处理方法中的各个阈值都是在大量资料分析的基础上得到的,并不固定,使用时需根据雷达资料的实际情况进行设置;可以根据不同的资料质量要求调整相应参数的阈值。阈值设置越苛刻,处理后得到的数据相对越少,数据的整体质量也越高,反之亦然。
| [1] | Seliga T A, Bringi V N. Potential use of radar differential reflectivity measurement at orthogonal polarizations for measuring precipitation. J Appl Meteor, 1976, 15: 69–76. DOI:10.1175/1520-0450(1976)015<0069:PUORDR>2.0.CO;2 |
| [2] | Doviak R J, Bringi V N, Ryzhkov A V, et al. Consideration for polarimetric upgrades to operational WER-88D radars. J Atmos Ocean Technol, 2000, 17, (3): 257–277. DOI:10.1175/1520-0426(2000)017<0257:CFPUTO>2.0.CO;2 |
| [3] | Gorgucci E, Chandrasekar V, Bringi V N, et al. Estimation of raindrop size distribution parameters from polarimetric radar measurements. J Atmos Sci, 2002, 59, (15): 2373–2384. DOI:10.1175/1520-0469(2002)059<2373:EORSDP>2.0.CO;2 |
| [4] | 曹俊武. 双线偏振多普勒雷达的资料质量控制及降水粒子相态识别方法的研究. 北京: 中国气象科学研究院, 2006. |
| [5] | 何宇翔, 吕达仁, 肖辉, 等. X波段双线极化雷达反射率的衰减订正. 大气科学, 2009, 33, (5): 1027–1037. |
| [6] | Hubbert J, Chandrasekar V, Bringi V N, et al. Processing and interpretation of coherent dual-polarized radar measurements. J Atmos Ocean Technol, 1993, 10, (4): 155–164. |
| [7] | Hubbert J, Bringi V N. An iterative filtering technique for the analysis of copolar differential phase and dual-frequency radar measurements. J Atmos Ocean Technol, 1995, 12, (3): 643–648. DOI:10.1175/1520-0426(1995)012<0643:AIFTFT>2.0.CO;2 |
| [8] | Ryzhkov A V, Zrnic D S. Discrimination between rain and snow with a polarimetric radar. J Appl Meteor, 1998, 17: 140–164. |
| [9] | Wang Yanting, Chandrasekar V. Algorithm for estimation of the specific differential phase. J Atmos Ocean Technol, 2009, 26, (12): 2565–2578. DOI:10.1175/2009JTECHA1358.1 |
| [10] | 曹俊武, 陈晓辉, 方文贵, 等. 双偏振多普勒雷达测量参数KDP的估算分析. 雷达科学与技术, 2010, 8, (1): 69–73. |
| [11] | Liu Liping, Hu Zhiqun, Fang Wengui, et al. Calibration and data quality analysis with mobile C-band polarimetric radar. Acta Meteor Sinica, 2010, 24, (4): 501–509. |
| [12] | Kostinski A. Fluctuations of differential phase and radar measurements of precipitation. J Appl Meteor, 1994, 33, (10): 1176–1181. DOI:10.1175/1520-0450(1994)033<1176:FODPAR>2.0.CO;2 |
| [13] | Ryzhkov A V, Zrnic D S, Burgess D, et al. Observation and Classification of Echoes with the Polarimetric WSR-88D Radar. Report of National Severe Storms Laboratory, Norman, Oklahoma, 2003: 19-26. |
| [14] | 丁青兰, 刘黎平, 葛润生, 等. 双线偏振多普勒雷达测量精度的理论分析. 应用气象学报, 2003, 14, (1): 30–38. |
| [15] | 曹俊武, 刘黎平, 陈晓辉, 等. 3836C波段双线偏振多普勒雷达及其在一次降水过程中的应用研究. 应用气象学报, 2006, 17, (2): 192–200. DOI:10.11898/1001-7313.20060210 |
| [16] | 程周杰, 刘宪勋, 朱亚平. 双偏振雷达对一次水凝物相态演变过程的分析. 应用气象学报, 2009, 20, (5): 594–601. DOI:10.11898/1001-7313.20090511 |
| [17] | 胡志群, 刘黎平, 肖艳娇. 降水粒子空间取向对双线偏振雷达观测影响模拟研究. 应用气象学报, 2008, 19, (3): 362–366. DOI:10.11898/1001-7313.20080313 |
| [18] | 东高红, 刘黎平. 雷达与雨量计联合估测降水的相关性分析. 应用气象学报, 2012, 23, (1): 30–39. |
 2012, 23 (6): 710-720
2012, 23 (6): 710-720



