目前,中尺度数值模式提供的定时、定点预报在精度上还存在较大偏差,预报效果不尽如人意。但目前对气象要素预报精度要求越来越高,特别是在举办一些大型活动,如阅兵式、露天文艺演出或体育比赛时,要求定时、定点的天气状况、温度、风向、风速等预报的细致程度就更加迫切。突出表现在2008年北京奥运会和残奥会期间,虽然各体育场馆对天气预报的服务内容要求不一,但其共同特点是预报越具体、越细致越好。因此在数值模式的预报结果满足不了社会需求的情况下,将数值预报产品通过一些动力和统计相结合的技术进一步加工、修正,以使要素预报的精度得到提高。这个动力和统计相结合的技术就是数值预报产品的解释应用。
数值预报产品的解释应用技术是将动力与统计方法相互结合,将两者的优点集合于一体,以达到定点、定时、定量的客观输出。动力学方法的优点在于它是在支配系统演变的物理规律的基础上,从因果制约上揭示其规律,克服了统计学方法中不论因果的缺陷。而统计学方法的优点则是收集模式系统的输出数据,建立数学模型,进行量化的分析、总结,消除数值预报模式的部分系统误差,进而作出更准确的推断和预测。在对模式预报的解释应用技术方面,最早由Klein等[1]于1959年提出,称为完全预报法 (Perfect Prognostic Method),通常简称PP预报。而后,Glathn等[2]于1972年提出了模式输出统计法 (Model Output Statistics),简称MOS法。MOS法的基本思路和PP法一样,认为天气情况取决于当时环流因子,因而在建模过程中预报量与预报因子的统计关系是同时性的。但前一种方法是利用历史实况数据进行统计,后一种方法是利用数值预报产品,通过统计方法建立预报量与预报因子的数学关系。因此,数值预报产品的解释应用是对数值预报的结果进行分析、订正,通过建立预报模型,给出要素预报的客观结果,为预报员提供客观的预报产品支持。
我国的气象工作者自国家气象中心陆如华、夏建国等于1985年引进美国MOS方法,利用B模式产品制作最高、最低气温24~72 h预报以来,解释应用工作持续至今。刘还珠等[3]研究并开发了适用于台站的气象要素预报的MOS预报系统,赵声蓉[4]进行了温度预报的多模式集成预报的研究,曾晓青等[5]、陈豫英等[6]研究了利用K最近邻域方法对降水和风进行预报,曹晓钟等[7]按照人工智能分类与集成的思想方法,利用前馈神经网络 (BP网络) 将T213模式、日本、德国的数值预报产品集成在一起,构成一个集成型的降水预报系统,王迎春等[8]利用卡尔曼滤波方法制作了北京9个地面自动站的风和温度预报。近几年,冯汉中等[9-10]将支持向量机 (SVM) 方法应用到站点气温的业务预报以及单站的晴雨预报中之后,有许多气象工作者,将SVM方法应用到降水、降水落区预报和温度、能见度预报等各类要素预报中。这些方法具有各自的优势,但除了MOS方法以外,在日常预报中运用并形成业务化,迄今为止仍不多见。北京市气象局自2008年将SVM方法应用于奥运场馆气象要素业务预报以来,还将SVM方法应用于基于每日8次的短期滚动预报模式北京快速循环更新数值预报系统 (BJ-RUC) 的乡镇温度业务预报中。该方法的业务化运行不仅在2008年北京奥运会和残奥会期间提供了奥运场馆气象要素预报服务,而且在北京市乡镇预报中发挥了重要作用。下一步,将继续利用SVM方法开发基于BJ-RUC预报的气象要素集合预报。
本文首先介绍SVM非线性回归建模选取的预报因子,然后,论述基于北京市气象局业务运行的中尺度模式MM5V3预报产品,应用SVM方法对北京市各气象站和奥运场馆的2 m温度、10 m风u,v分量和2 m比湿等气象要素进行定点、定时、定量预报的研究概况,并重点对奥运会和残奥会期间 (2008年8月6日—9月20日) 的12:00(世界时,下同) 起始预报结果进行检验,与原数值预报模式直接输出的要素预报对比,评价经过解释应用后的预报效果。同时,为了进一步说明SVM方法的非线性回归的优势,与同时期利用多元线性回归的MOS方法提供的要素解释应用预报的结果进行比较,以便探讨SVM非线性回归方法有助于提高某些气象要素预报效果的潜在因素。
1 资料处理和SVM建模预报因子简介收集整理北京奥运场馆2006年和2007年的6—9月资料,形成样本集,运用SVM方法[11-12]对所得到的样本进行参数调优建模,利用所建模型对2008年6—9月北京奥运场馆站点要素提供业务预报。本文在介绍支持向量机非线性回归方法[13-15]实现奥运场馆站点气象要素建模和预报的基础上,针对2008年北京奥运会和残奥会 (2008年8月6日—9月20日) 期间奥运场馆站点气象要素的业务解释应用 (以下简称释用) 预报进行检验,并与原中尺度模式MM5V3直接输出的要素预报进行对比。结果显示:在原数值模式预报的基础上,释用预报能够提供更加精确的场馆气象要素预报。
应用基本的SVM非线性回归方法建模对北京15个奥运场馆 (图 1) 包括国家体育场、奥林匹克森林公园射箭场、奥体中心体育馆、北京大学体育馆、北京射击馆、北京理工大学体育馆、老山自行车馆、五棵松棒球场、丰台垒球场、工人体育场、沙滩排球场、北京工业大学体育馆、铁人三项赛场、顺义奥林匹克水上中心、城区自行车公路赛场的2 m温度、10 m风u,v分量和2 m比湿提供6~48 h站点气象要素逐3 h的业务释用预报。

|
|
| 图 1. 北京奥运场馆分布图 Fig 1. The map of Olympic venues in Beijing | |
利用MM5V3模式3 km区域预报,中心点为40°N,116°E,199×172经纬网格,网格距为3 km,最小和最大经纬度顶点分别为37.613°N,112.645°E和42.355°N,119.852°E,将模式部分预报结果和自动站部分实况作为预报因子,统计2006年和2007年的6—9月所能获取的全部样本,逐站点、逐时次、逐气象要素进行建模。为了避免各预报因子量级的差异,消除预报因子的单位和量纲的影响,统一对预报因子进行归一化,具体归一化公式为
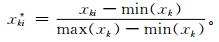
|
(1) |
式 (1) 中,xki*为归一化后的第k个预报因子值,其值范围为[0, 1],xki为第k个预报因子的原值,min (xk) 和max (xk) 分别为第k个预报因子的最小值、最大值,为了尽量避免出现相应预报因子值对于其最大值、最小值的溢出,对最大值加其绝对值的0.1倍,对最小值减去其绝对值的0.1倍,即将原来最大值、最小值区间扩展到原来的1.1倍。
|
|
表 1 利用SVM方法建模选取的预报因子 Table 1 Selected forecast factors for SVM method |
其中模式预报因子均选取站点周围4个格点同预报时次的模式预报量作为预报因子;实况因子选取预报初始时刻的该站点观测资料。
MOS方法基于2004—2007年国家气象中心T213全球模式预报结果,分季节对北京各奥运场馆站点建模,提供12:00起报的6~48 h的北京奥运场馆气象要素预报结果,其中T213模式39 h和45 h时效没有输出结果,因此这两个预报时次不参与预报检验。这里要注意的是,没有利用MM5V3模式的产品制作的MOS预报,而是利用较长时间的国家气象中心的T213模式预报结果。
由于数值模式预报存在一定的时间滞后,因此具有预报效果的北京奥运场馆要素预报从6 h预报开始。下面对2008年8月6日—9月20日共计46 d,12:00起报的6~48 h的2 m温度、10 m风u,v分量、2 m比湿或2 m相对湿度预报,对比检验SVM释用预报,MOS释用预报和MM5V3,T213模式直接输出的预报结果 (模式直接输出站点气象要素预报为利用最近4个格点根据双线性插值得到)。将SVM释用预报与MM5V3模式直接输出的要素预报进行比较,可以看到SVM释用预报对提高要素预报的作用和贡献。MOS释用预报是利用较长时段的T213模式预报的资料建立预报模型,应该是具备比较稳定的预报性能,以该模型得出的预报结果与T213直接输出的预报相比较可以客观地反映出MOS释用技术能力。只是该MOS方法并非以MM5V3模式产品 (历史资料较短) 为基础,两种模式产品的差异可能会对预报建模的效果有些影响,因此两种释用技术预报结果的比较不够严格,但也不会产生很大差异,可以作为参考。另外,为了弥补这两种方法所建立的数值预报产品不一致的缺陷,这里特别将它们各自的预报结果与其自身模式预报产品相比较,得出各自预报误差的减小百分率。通过误差的减小百分率,可以体现出两种方法对模式产品的释用能力,如果减小百分率大,说明减小预报误差的效果好,其释用能力强。
北京15个奥运场馆各预报时次平均的SVM,MOS释用预报和MM5V3,T213模式预报的均方根误差和预报偏差,以及释用预报的均方根误差相对模式直接输出预报均方根误差减小百分率,其表达式如下:
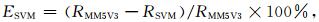
|
(2) |

|
(3) |
其中,E为误差减小百分率,R为预报的均方根误差。
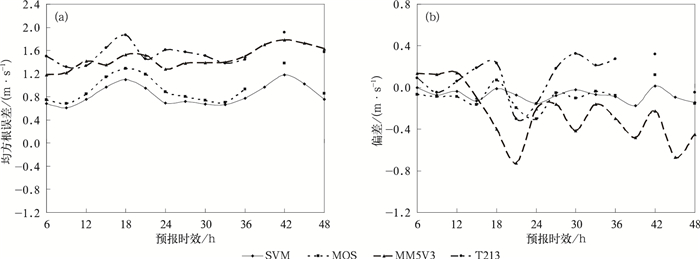
2 北京奥运场馆气象要素释用预报检验 2.1 2 m温度预报检验图 2给出SVM,MOS释用和MM5V3,T213模式预报对北京15个奥运场馆平均2 m温度预报的均方根误差和预报偏差对比。由图 2可以看出,在15个时次的预报中,SVM预报效果较好的有10个时次,MOS预报有5个时次,SVM释用预报略优于MOS释用预报,T213模式2 m温度插值到站点后的预报效果较差,均方根误差均在4℃以上。从预报偏差来看,MOS预报以偏暖为主,而SVM释用预报冷暖比例相当,T213模式预报的系统偏差非常明显,经过MOS释用后从T213系统性偏冷-4℃以上变为1℃以内正偏差。

|
|
| 图 2. SVM,MOS释用预报和MM5V3,T213模式预报北京15个奥运场馆平均2 m温度均方根误差 (a) 和预报偏差 (b) 对比 Fig 2. The 2 m temperature root mean square error (a) and bias (b) of 15 Olympic venues in Beijing provided by SVM-release, MOS-release, MM5V3 model and T213 model | |
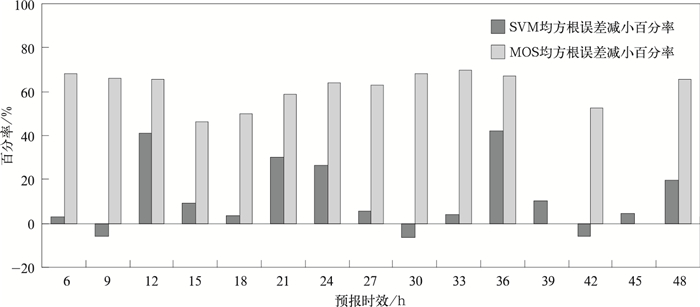
图 3为SVM和MOS释用预报相对原模式预报均方根误差减小百分率,不难看出,SVM释用预报有3个时次的预报效果略差于MM5V3模式预报,以12,21,24,36,48 h的释用效果最好,均方根误差减小均达到20%以上。MOS释用预报相对T213的预报效果均有显著改善,均方根误差减小百分率均在40%以上。从各时次均方根误差减小百分率的平均来看,SVM相对于MM5V3模式预报减小12.1%,MOS相对于T213模式预报减小61.9%,MOS释用幅度远大于SVM。由此可以看出,对于温度,一方面,其数据属于正态分布,另一方面,由于温度与预报因子之间的相关系数较稳定且相关性较好,表明它与预报因子之间有较好的线性相关。因此,使用多元回归的MOS方法释用效果非常显著,将原来T213模式4℃以上的均方根误差降低为2~3℃左右。与SVM方法预报的均方根误差相差不多,说明MOS方法对温度的释用预报效果较好。
|
|
| 图 3. 2 m温度SVM释用预报、MOS释用预报相对原模式预报均方根误差减小百分率 Fig 3. The decreased root mean squre error ratio of 2 m temperature forecast from SVM-release, MOS-release to the counterpart of direct output of model | |
如果定义2 m温度预报准确率为绝对偏差在2℃以内的预报数占总预报数的百分率,SVM释用2 m温度预报的准确率为66.5%,MOS释用2 m温度预报的准确率为62.2%,MM5V3模式2 m温度预报的准确率为58.8%,T213模式2 m温度预报的准确率为2.5%。相对而言,SVM方法预报效果略优于MOS方法,但相对原模式预报,MOS释用效果显著。
2.2 10 m风u,v分量预报检验图 4为SVM,MOS释用预报和MM5V3,T213模式预报北京15个奥运场馆平均10 m风u分量均方根误差和预报偏差的对比。由图 4可以看出,10 m风u分量的预报北京15个预报时次均以SVM释用预报的预报效果较好。相对于原模式,释用后的预报效果均有显著改善,10 m风u分量均方根误差绝大部分时次均在1 m·s-1以内。从预报偏差来看,原MM5V3模式预报以负偏差为主,T213模式预报以正偏差为主,说明MM5V3模式预报的西风偏小,而T213模式预报的西风偏大,经过释用整体呈现负的偏差且幅度明显变小,说明数值预报西风的系统性偏差得到改善,这也反应出经过释用后10 m风u分量的预报精度提高。
|
|
| 图 4. SVM,MOS释用预报和MM5V3,T213模式预报北京15个奥运场馆平均10 m风u分量均方根误差 (a) 和预报偏差 (b) 对比 Fig 4. The 10 m wind u component root mean square error (a) and bias (b) of 15 Olympic venues in Beijing provided by SVM-release, MOS-release, MM5V3 model and T213 model | |
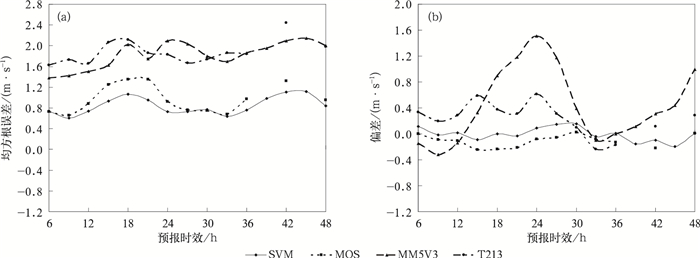
由10 m风v分量的预报结果 (图 5) 可见,13个预报时次SVM释用预报的预报效果较好,2个预报时次的MOS释用预报效果较好,相对于原模式,释用后的预报均有显著改善,均方根误差绝大部分预报时次均在1 m·s-1以内,结合10 m风u分量的释用预报,能提供比较精确的北京奥运场馆10 m风预报。从预报偏差来看,模式预报以正偏差为主,说明数值模式预报的北风偏大,经过SVM或MOS释用后,偏大的幅度明显减小,偏差均接近于0,说明释用后能有效改善模式预报北风偏大的系统性误差。模式的24 h预报正偏差偏大,反应模式预报对北京日夜更替时南北风转向的预报效果不尽如人意,经过释用后大的偏差得以消除,这些均反映出经过释用后10 m风v分量的预报精度提高。
|
|
| 图 5. SVM,MOS释用预报和MM5V3,T213模式预报北京15个奥运场馆平均10 m风v分量均方根误差 (a) 和预报偏差 (b) 对比 Fig 5. The 10 m wind v component root mean square error (a) and bias (b) of 15 Olympic venues in Beijing provided by SVM-release, MOS-release, MM5V3 model and T213 model | |
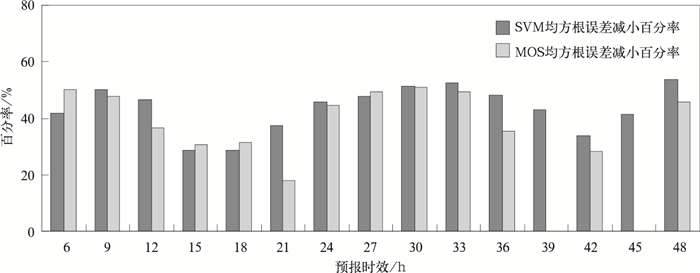
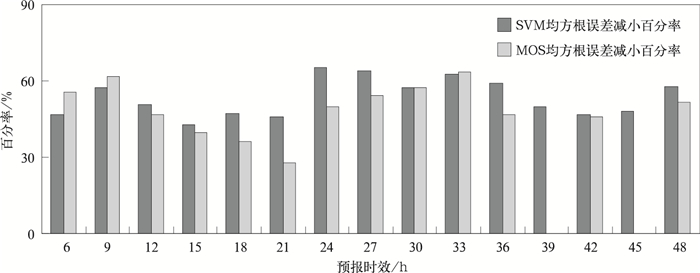
图 6和图 7分别为10 m风u,v分量6~48 h逐3 h的SVM,MOS释用预报相对原模式预报均方根误差减小百分率。可以看出,释用后的预报效果在原模式预报的基础上均有显著改善。SVM释用预报对比原MM5V3模式预报,10 m风u分量的均方根误差减小百分率绝大部分在30%以上,10 m风v分量的均方根误差减小百分率均在40%以上。从各预报时次均方根误差减小百分率的平均来看,相对于原MM5V3模式预报,SVM释用的10 m风u分量减小43.3%,10 m风v分量减小53.4%,同期MOS释用预报相对T213预报10 m风u分量减小39.4%,10 m风v分量减小49%。综合SVM,MOS均提供释用预报的u,v分量26个时次中,均方根误差减小百分率有19个时次SVM占优势,7个时次MOS占优势。
|
|
| 图 6. 10 m风u分量SVM释用预报、MOS释用预报相对原模式预报均方根误差减小百分率 Fig 6. The decreased root mean square error ratio of 10 m wind u component forecast from SVM-release, MOS-release to the counterpart of direct output of model | |
|
|
| 图 7. 10 m风v分量SVM释用预报、MOS释用预报相对原模式预报均方根误差减小百分率 Fig 7. The decreased root mean square error ratio of 10 m wind v component forecast from SVM-release, MOS-release to the counterpart of direct output of model | |
如果定义10 m风u,v分量预报准确率为绝对偏差在1 m·s-1以内的预报数占总预报数的百分率,SVM释用10 m风u, v分量预报的准确率分别为77.6%和76.7%,而MM5V3模式10 m风u, v分量预报的准确率分别为54.5%和41.1%,通过SVM释用的风场预报有较大的改善。MOS释用10 m风u, v分量预报的准确率分别为75.8%和73.7%,T213模式10 m风u, v分量预报的准确率分别为46.9%和34.9%。可以看出,MOS方法对风场的预报释用准确率也有较大提高。从预报量和预报因子之间的相关系数来看,10 m风除了和近地面975 hPa的u,v分量相关性较好以外,与其他建模预报因子相关性均较差,说明预报量和预报因子之间主要为非线性相关;同时大气边界层的运动形态一般是湍流的,而湍流是高度非线性的[16],这更加剧了10 m风场与预报因子的非线性的关系。由SVM方法对10 m风场预报释用后均方根误差减小百分率优于MOS方法来看,SVM方法在处理非线性问题上具有一定的优势。
2.3 2 m比湿或2 m相对湿度预报的检验结果由于MM5V3模式和SVM释用均直接给出的是2 m比湿预报,因此,利用SVM相对于MM5V3模式的均方根误差减小率来检验2 m比湿。而T213模式和MOS释用均直接给出2 m相对湿度预报,因此,利用MOS相对于T213的均方根误差减小率来检验2 m相对湿度预报。
从2 m比湿预报均方根误差来看 (图 8),所有预报时次均以SVM释用的预报效果较好,相对来看MOS预报释用效果并不明显,这也许与MOS预报的比湿是由其预报的2 m温度、本站气压以及相对湿度计算得到有一定关系,因为2 m温度、本站气压和相对湿度本身预报就存在一定误差,利用它们计算2 m比湿,很显然这些误差会传递而造成2 m比湿的较大误差。SVM释用后,2 m比湿的均方根误差均在2 g·kg-1以内,预报精度在原模式预报的基础上有明显改善。从2 m相对湿度MOS和T213模式预报均方根误差来看,前几个时次释用效果明显,往后释用效果变弱,后几个时次略差于模式预报。从预报偏差来看 (图略),模式预报均以偏湿为主,平均偏差均为正的偏差,释用后预报偏差正负均有且绝对值均变小,精度改善。

|
|
| 图 8. SVM, MOS释用预报和MM5V3模式预报2 m比湿 (a) 以及MOS和T213预报2 m相对湿度 (b) 北京15个奥运场馆平均均方根误差对比 Fig 8. The 2 m specific humidity root mean square error provided by SVM-release, MOS-release (a), MM5V3 model, and the 2 m relative humidity root mean square error provided by MOS-release, T213 model (b) of 15 Olympic venues in Beijing | |
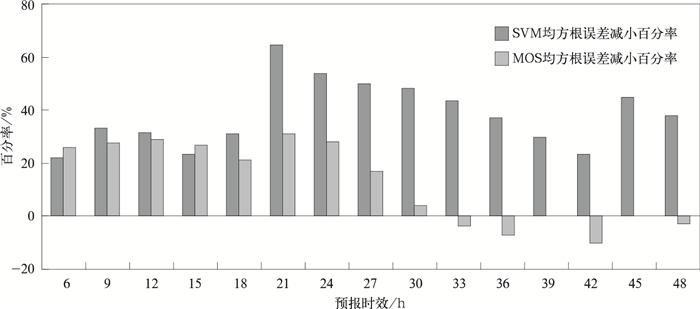
从图 9的2 m比湿或2 m相对湿度释用预报相对原模式预报均方根误差减小百分率可以看出,SVM释用预报相对原模式预报均方根误差减小百分率均在20%以上,释用效果显著。MOS释用预报前期效果明显,随着预报时间的增长,释用效果变差,最后几个预报时次略差于T213模式预报。从各时次均方根误差减小百分率的平均来看,相对原模式预报,SVM预报减小38.2%,MOS预报减小14.3%。由此看来,SVM方法释用效果高于MOS方法。从预报量和预报因子之间的相关系数来看,除了与相对湿度和温度露点差的相关性较好以外,与其他预报因子之间相关性均较差,说明湿度与预报因子之间主要为非线性关系。由此,亦显示出了SVM方法对处理非线性问题的能力优于MOS方法。
|
|
| 图 9. 2 m比湿SVM释用预报相对MM5V3及2 m相对湿度MOS释用预报相对T213模式均方根误差的减小百分率 Fig 9. The decreased root mean square error ratio of 2 m specific humidity forecast from SVM-release to MM5V3 model, and the decrease root mean square error ratio of 2 m relative humidity forecast from MOS-release to T213 model | |
如果定义2 m比湿预报准确率为绝对偏差在2 g·kg-1以内的预报数占总预报数的百分率,SVM释用2 m比湿预报的准确率为84.9%,MOS释用2 m比湿预报的准确率为67.8%,MM5V3模式2 m比湿预报的准确率为61.7%。整体来说,SVM方法在处理非线性问题上具有一定的优势。
3 结论和讨论利用基本的SVM非线性回归释用预报方法,制作北京奥运场馆站点6~48 h逐3 h的气象要素预报,并提供2008年北京奥运会和残奥会期间15个奥运场馆气象要素预报服务。得出以下结论:
1) 对比MM5V3预报要素的直接输出,SVM释用预报精度有显著提高,从各时次的预报要素均方根误差平均减小率来看,2 m温度减小12.1%,10 m风u分量减小43.3%,10 m风v分量减小53.4%,2 m比湿减小38.2%。
2) 与同期MOS释用方法预报的结果比较,2 m温度、10 m风u, v分量的预报效果SVM略优于MOS,2 m比湿的预报效果SVM明显优于MOS。对某些要素预报,如风、比湿等具有非线性特点的要素,SVM释用预报具有一定优势。当预报量和预报因子之间存在明显线性关系时,MOS建模预报相对原模式直接预报误差减小百分率较高,释用预报效果较好,这种情况下,SVM释用方法的优势就不够明显了。而且SVM建模的过程较MOS方法复杂得多,花费时间也更多,这也是SVM方法不易在业务上普及推广的缘故。
由于该释用预报具有很强的针对性,在2008年北京奥运会后就停止业务运行,预报连续性不够。2010年基于北京地区每日8次的短期滚动预报模式BJ-RUC预报产品,利用SVM方法,提供北京98个乡镇站点的2 m温度业务预报。下一步将该方法继续应用在基于BJ-RUC的地面气象要素集成预报中,使之发挥更大的效用。
| [1] | Klein W H, Lewis F B M, Enger I. Objective prediction of five-day mean temperatures during winter. J Meteorol, 1959, 16: 672–682. DOI:10.1175/1520-0469(1959)016<0672:OPOFDM>2.0.CO;2 |
| [2] | Glahn H R, Lowry D A. The use of Model Output Statistics (MOS) in objective weather forecasting. J Appl Meteor, 1972, 11: 1203–1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2 |
| [3] | 刘还珠, 赵声蓉, 陆志善, 等. 国家气象中心气象要素的客观预报——MOS系统. 应用气象学报, 2004, 15, (2): 181–191. |
| [4] | 赵声蓉. 多模式温度集成预报. 应用气象学报, 2006, 17, (1): 52–58. DOI:10.11898/1001-7313.20060109 |
| [5] | 曾晓青, 邵明轩, 王式功, 等. 基于交叉验证技术的K-NN方法在降水预报中的试验. 应用气象学报, 2008, 19, (4): 471–478. DOI:10.11898/1001-7313.20080411 |
| [6] | 陈豫英, 刘还珠, 陈楠, 等. 基于聚类天气分型的KNN方法在风预报中的应用. 应用气象学报, 2008, 19, (5): 564–572. DOI:10.11898/1001-7313.20080507 |
| [7] | 曹晓钟, 闵晶晶, 刘还珠, 等. 分类与集成方法在降雨预报中的应用. 气象, 2008, 34, (10): 3–11. DOI:10.7519/j.issn.1000-0526.2008.10.001 |
| [8] | 王迎春, 刘凤辉, 张小玲, 等. 北京地区中尺度非静力数值预报产品释用技术研究. 应用气象学报, 2002, 13, (3): 312–321. |
| [9] | 冯汉中, 陈永义. 支持向量机回归方法在实时业务预报中的应用. 气象, 2005, 31, (1): 41–44. DOI:10.11676/qxxb2005.005 |
| [10] | 冯汉中, 杨淑群, 刘波. 支持向量机 (SVM) 方法在气象预报中的个例试验. 四川气象, 2005, 25, (2): 9–12. |
| [11] | Vapnik V N. Statistical Learning Theory. New York: John Wiley & Sons Inc, 1998. |
| [12] | Vapnik V N. The Nature Of Statistical Learning Theory. New York: Springer Verlag, 2000. |
| [13] | 陈永义, 俞小鼎, 高学浩, 等. 处理非线性分类和回归问题的一种新方法 (Ⅰ)——支持向量机方法简介. 应用气象学报, 2004, 15, (3): 345–354. |
| [14] | 冯汉中, 陈永义. 处理非线性分类和回归问题的一种新方法 (Ⅱ)——支持向量机方法在天气预报中的应用. 应用气象学报, 2004, 15, (3): 355–365. |
| [15] | Scholkopf B, Burges C J C, Smola A J. Advance in Kernel Methods Support Vector Learning. Cambridge: MIT Press, 1999. |
| [16] | 盛裴轩, 毛节泰, 李建国, 等. 大气物理学. 北京: 北京大学出版社, 2003. |
 2012, 23 (5): 562-570
2012, 23 (5): 562-570



