遥感图像作为空间数据，具有空间地理位置的概念。无论何种应用问题，都要确定图像信息与地面位置的对应关系。遥感图像的地理定位是计算星载遥感仪器观测图像在地基坐标系中坐标的处理过程。地理定位需要考虑仪器扫描几何、仪器空间位置和指向、地球曲率、地形以及仪器运动中产生的微小扰动等因素。卫星遥感数据的几何形变可以分为系统性形变和非系统性形变。系统性形变多由遥感仪器本身造成，非系统性形变则主要因为遥感仪器的运动、地球的扁率和旋转以及地形而产生。

计算卫星遥感图像地理位置的方法分为参数法和非参数法。非参数法需要具有明显地物特征且已知地理位置的地面点，即通常意义的地面控制点 (GCP)，来建立遥感数据和地基坐标系之间空间位置关系的模型。非参数法可以用于所有类型的几何形变^[1-2]，但非参数方法并不适用于业务运行中的卫星遥感图像地理定位，因为高精度地面控制点的选取需占用大量时间和资源，且很难在有云的情况下识别可用的地面控制点。非参数法无法满足高时效性和高稳定性的气象卫星业务需求。参数法是根据遥感仪器观测几何及其空间位置和指向，建立观测像元与地面观测位置之间的模型。地面控制点则用于消除由于这些参数的不确定性导致的地理定位误差^[3-4]。地形信息用来消除由地表地形带来的地理定位误差，该误差与卫星高度、地形以及观测点与星下点的距离有关^[5]。

AVHRR和MODIS等大气遥感仪器的地理定位方法均使用参数法^[6-7]。而IKONOS，QuickBird等高分辨率遥感影像则使用非参数法进行地理定位，发展了诸如DLT^[8]，SDLT^[9]，RATM^[10]，基于卫星参数预测定位^[11]等模型。

中分辨率光谱成像仪 (MERSI) 是我国极轨气象卫星风云三号A星 (FY-3A) 的有效载荷之一。FY-3A卫星于北京时间2008年5月27日上午成功发射。MERSI于2008年6月4日开机成功接收第1幅遥感图像。MERSI是类似MODIS的遥感仪器，独具特色的250 m分辨率红外通道能全天候获取遥感信息，其遥感图像地理定位方法采用参数法。MERSI遥感图像地理定位产品包括地理经纬度、高程、仪器和太阳的天顶角方位角以及斜距。这些数据可供MERSI遥感数据的投影变换和产品使用。本文介绍了MERSI遥感图像地理定位处理方法，并分析了地理定位误差。

我国极轨气象卫星FY-3A是近极地太阳同步轨道卫星，轨道高度831 km，轨道倾角98.8°。卫星轨道回归周期为5 d，降交点地方时为10:05。MERSI是FY-3A卫星的有效载荷之一，有20个探测波段，可以同时获取丰富的地气辐射景象，实现对陆地、大气、海洋的全球动态监测。

MERSI安装在卫星的对地面，开口朝向地球。采用45°旋转扫描反射镜 (简称45°扫描镜) 旋转扫描，扫描镜的转轴与卫星的飞行方向一致。当扫描镜转动时，扫描镜以固定的瞬时视场做穿越飞行轨迹的扫描，接收与轨道垂直平面内的目标辐射，借助卫星的绕地球运行获取地球二维景像。

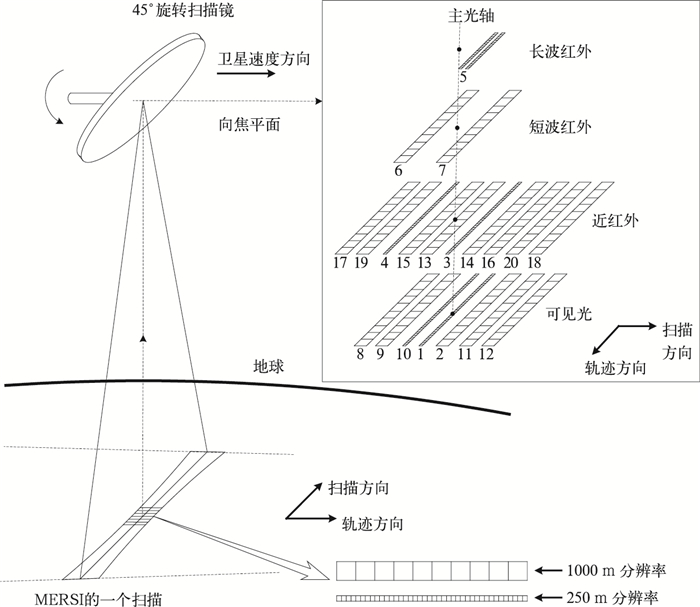
MERSI采用了10元、40元探测器并扫的方案，即扫描镜每旋转一圈，在卫星飞行方向同时扫过10条、40条扫描线，对应地面分辨率为1000 m和250 m，每条扫描线的采样点分别为2048和8196。图 1为MERSI观测地球景像的原理图。

图 1

图 1. MERSI扫描几何 Fig 1. Overview of MERSI sensing geometry

MERSI有10个可见光波段、7个近红外波段、2个短波红外波段和1个热红外波段，分别在4个焦平面上成像。对应这些波段有20个探测器列，探测器列平行排列在4个不同的焦平面上。每个波段的探测器列在焦平面上沿扫描方向排列。探测器的位置和焦距决定了各焦平面与仪器光轴的几何关系。

MERSI的对地扫描观测角为55.1°，它可以每天覆盖全球2次。45°扫描镜的转速为40转/min，扫描周期为1.5 s，其中约0.46 s为对地观测时间，对应1000 m分辨率的通道，即每行采样2048个像素点，每个采样点的驻留时间约为224 ms。

为消除45°扫描镜在观测目标偏离星下点时带来的像旋转，MERSI的主光学系统后插入了一个像消旋装置。该系统由另一台高精度步进电机驱动，以20转/min的速度绕其转轴 (与光轴一致) 旋转，达到消除像旋转的目的。像消旋装置由像消旋驱动电机、轴承、K镜、平面镜、壳体、基准信号发生器等部分组成。K镜是一个全波段反射系统，由3个平面反射镜组成，当它的转角始终保持为45°扫描镜转角的一半时，像不旋转，达到消除像偏转的目的。因其三面反射镜呈“K”字排列故起名K镜^[12]。

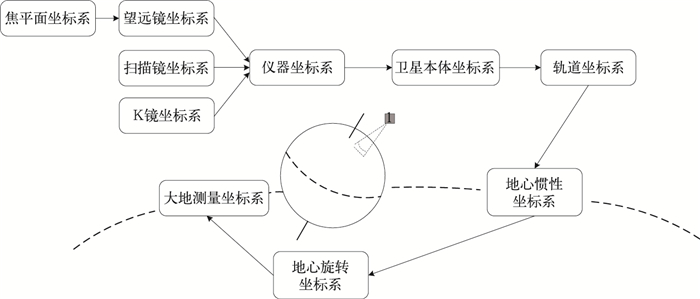
在MERSI遥感数据地理定位算法中，共用到了10个基本坐标系。分别是焦平面坐标系 (foc)、扫描镜坐标系 (mirr)、望远镜坐标系 (tel)、K镜坐标系 (Kmirr)、仪器坐标系 (inst)、卫星本体坐标系 (SC)、轨道坐标系 (Orb)、地心惯性坐标系 (ECI)、地心旋转坐标系 (ECR) 和大地测量坐标系 (表 1)。地心惯性坐标系为J2000.0地心惯性系 (也称J2000.0平天球坐标系)^[13]，地心旋转坐标系采用WGS-84直角坐标系，大地测量坐标系基于WGS84参考椭球体，坐标为经度、纬度、高程^[14]。大地测量坐标系与地心旋转坐标系的不同在于地心旋转坐标系与地球参考椭球体无关，而大地测量坐标系需依赖地球参考椭球体。这10个基本坐标系之间的转换关系见图 2。

表 1

表 1 各种坐标系定义 Table 1 Definition of coordinate systems 坐标系 原点 参考平面 x轴方向 z轴方向 焦平面坐标系 系统光轴与焦平 面的交点 焦平面 沿扫描方向 与焦平面垂直指向焦 点方向 扫描镜坐标系 45°扫描镜与系统 光轴的交点 沿45°扫描镜的旋转轴 方向 45°扫描镜中心点指向 星下点的方向 望远镜坐标系 系统光轴与焦平 面的交点 x轴垂直于扫描镜的旋 转轴，并且沿光线经扫 描镜在0°扫描角时反 射之后的扫描方向 平行于系统光轴指向 卫星飞行方向 K镜坐标系 K镜的几何中心 与系统光轴的交点 沿K镜的旋转轴方向 与扫描镜坐标系z轴方 向一致 仪器坐标系 仪器质心 仪器安装平面 与卫星滚动轴指向一致 与卫星偏航轴指向一致 卫星本体 坐标系 卫星质心 卫星滚动轴与俯 仰轴所在平面 与卫星滚动轴指向一致 与卫星偏航轴指向一致 轨道坐标系 卫星质心 卫星轨道平面 与卫星速度方向一致 从卫星质心指向地心 地心惯性 坐标系 地心 J2000.0平赤道面 指向J2000.0的平春分点 指向J2000.0的平北天极 地心旋转 坐标系 地心 国际时间局 BIH1984.0时元定 义的协议地球赤 道面 指向国际时间局 BIH1984.0时元定义的 零子午面和协议地球 赤道的交点 平行于国际时间局 BIH1984.0时元定义的 协议地球极轴方向 大地测量 坐标系 地心

表 1 各种坐标系定义 Table 1 Definition of coordinate systems

图 2

图 2. 各坐标系之间转换关系 Fig 2. Transformation of coordinate systems

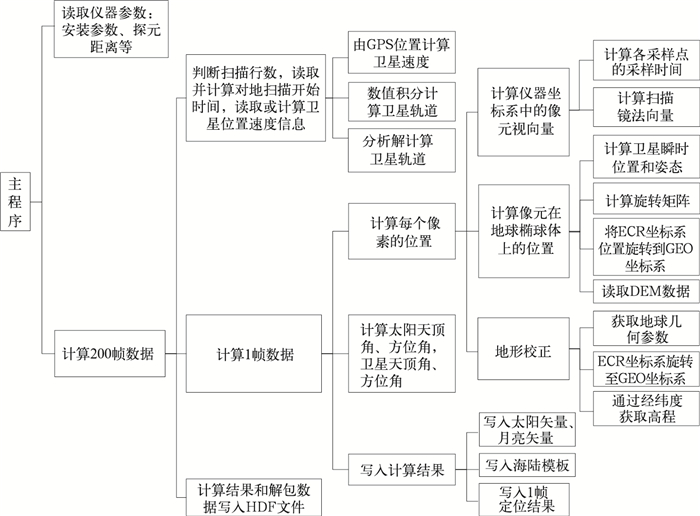
对MERSI观测像元做地理定位，首先根据仪器观测几何建模，计算观测像元在仪器坐标系中的视向量，之后通过各参数计算像元在地球表面位置，完成地理定位计算。流程如图 3所示。

图 3

图 3. MERSI地理定位流程图 Fig 3. Flow chart of MERSI geolocation

FY-3A卫星的轨道数据使用星载GPS实时测量数据或者根据轨道根数通过高精度数值积分计算的结果；卫星姿态数据由星载陀螺仪和星敏感器测量获得。MERSI仪器的安装参数以及FY-3A卫星平台参数在卫星发射前测量得到，保存在参数文件中，在地理定位过程中被定位程序反复读取。使用全球数字高程模型 (DEM) 来消除地形对遥感图像地理定位精度的影响^[15]。

虽然MERSI采用了类似MODIS的通道设置，但是它们之间的观测特性有差别，主要体现在扫描镜的扫描方式上。MODIS采用双面镜扫描成像，而MERSI采用45°旋转扫描反射镜成像。这两种扫描镜各有优缺点：双面镜两个镜面交替使用，必须使两个镜面的反射特性严格一致，这在加工工艺上要求较高；且遥感器在轨工作后，对两个镜面的衰减情况要有监测，这一点在太空中难以实现。双面镜的优势是对于多元并扫成像仪器，不会产生像旋现象。由于45°旋转扫描镜只有一个镜面工作，所以不存在两个镜面衰减监测的问题，但对多元并扫的情况，其会使所成的像在焦平面上产生旋转。

为了弥补45°扫描镜的不足，MERSI采用了K镜机构，在物理硬件上消除了像旋现象。体现在算法模型中，要求模型的坐标系系统加入K镜坐标系，通过K镜坐标系的转换，实现计算像元的定位结果^[16]。

此外，在MERSI定位算法流程中，使用GPS数据和高精度轨道积分模型 (IOE) 数据，获取卫星位置速度等参数。优先使用GPS的位置速度信息，在GPS数据不可用或者缺失的情况下，使用IOE数据。这样能够保证业务系统运转的实效性和稳定性。

造成遥感图像地理定位误差与计算中所使用的基础测量数据的不确定度密切相关。卫星位置偏差、卫星姿态偏差以及仪器安装误差是造成图像定位结果偏差的主要来源。无论在扫描方向还是轨迹方向，卫星位置的误差均与地理定位的误差成比例^[17]。卫星在轨道坐标系x轴方向的位置误差仅对轨迹方向定位误差有贡献，y和z轴位置误差仅对扫描方向定位误差有贡献。卫星姿态、遥感仪器指向偏差会导致地理定位的误差。滚动姿态误差导致沿扫描方向的地理定位偏差，这个偏差随着扫描角的增大而增大，在星下点处最小而最大扫描角处最大。俯仰和偏航在扫描方向带来非常小的定位误差，这个误差在星下点两侧对称分布且非线性增大，从星下点到最大扫描角处从零增至最大。在卫星轨迹方向，俯仰姿态误差导致的误差是常数，滚动误差不会带来定位误差，偏航在轨迹方向带来的误差与它在扫描方向带来的误差方式一致，只是误差值更大。FY-3A卫星高度为831 km，地球平均半径为6371 km，10″的偏差在滚动方向会在星下点处带来48 m的定位偏差，在扫描边缘 (55.1°扫描角) 处带来223 m的定位误差。在轨迹方向俯仰角10″的偏差会在星下点和扫描边缘分别带来48 m的定位误差。同样轨迹方向偏航角10″的误差会在星下点到扫描边缘带来从0~84 m的定位误差。

导致地理定位误差的误差源可分为动态误差源和静态误差源两类。动态误差源包括轴承、扫描镜控制系统、扫描角精度、仪器热变形和结构形变、卫星姿态测量精度、卫星位置测量精度以及卫星的热变形和结构形变等，这些误差源是随时间变化的，其变化行为很难模拟。静态误差源包括仪器的热变形和结构形变、扫描镜的热变形和结构形变、探测器和扫描镜以及仪器的安装偏差，还有星敏感器的系统误差 (恒星位置偏差) 等，这些误差不随时间变化，可以通过地面处理减小或消除^[18-20]。

此外，地形和大气折反射也会对遥感图像地理定位精度造成影响。地形对定位精度的影响是扫描角的函数，越到图像边缘影响越明显。虽然可以用DEM来消除地形带来的定位误差，但DEM数据本身也存在误差。地形校正处理时的插值计算也会来带定位误差。MERSI遥感图像地理定位采用30″分辨率的DEM数据，来自美国国家影像与制图局 (NIMA) 和世界数字化图 (DCW) 数据^[21]，DEM数据中73%的陆表数据存在59 m的高程误差，其他数据的精度更低一些。

根据前面的分析，引起卫星遥感数据地理定位误差的原因主要有5种：卫星位置误差、卫星姿态误差、遥感仪器-卫星平台安装误差、遥感仪器内部几何误差以及卫星和遥感仪器的热变形和结构形变。为减小和消除MERSI遥感图像地理定位的误差，本文使用一定数量的地面控制点来分析和消除由上述误差源带来的遥感图像地理定位误差。在卫星发射后，由卫星姿态和卫星位置偏差导致的遥感图像地理定位误差不可能完全区分开来。虽然卫星发射前仪器的安装矩阵已经测出，但在卫星发射过程中以及在轨运行期间由于外部环境的改变可能会造成仪器安装位置的微小变化。通过地面控制点的位置偏差分析，将所有静态误差等效为卫星的姿态偏差或仪器的安装偏差。而动态误差的修正则需要在消除了静态误差之后，再通过长时间序列的遥感图像地理定位结果分析来完成。

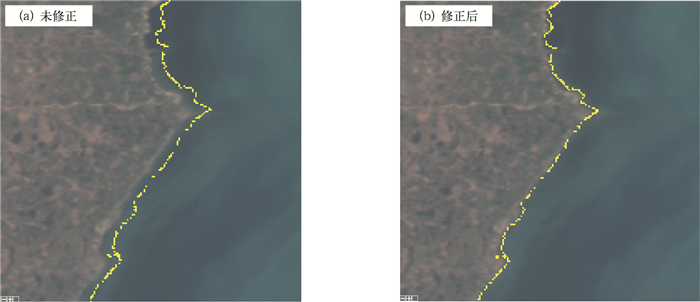
应用文中方法对MERSI遥感图像进行地理定位计算，计算结果如图 4a、图 5a、图 6a所示。图中的遥感图像分别是FY-3A MERSI 2009年2月11日03:10(世界时，下同)，04:55和06:30的250 m分辨率通道1(470 nm)、通道2(550 nm) 和通道3(650 nm) 的真彩色合成图。图中的黄色曲线是由地理定位计算结果在GSHHS数据库中检索到的相应水陆分界线，它与遥感图像的密合程度直接反映了地理定位的精度。

图 4

图 4. 中国海南省西部地区遥感图像地理定位结果 Fig 4. MERSI geolocation of Hainan west coastline in China

图 5

图 5. 也门南部亚丁湾地区遥感图像地理定位结果 Fig 5. MERSI geolocation of Gulf of Aden in South Yemen

图 6

图 6. 印度南部保克海峡地区遥感图像地理定位结果 Fig 6. MERSI geolocation of Palk Strait in South India

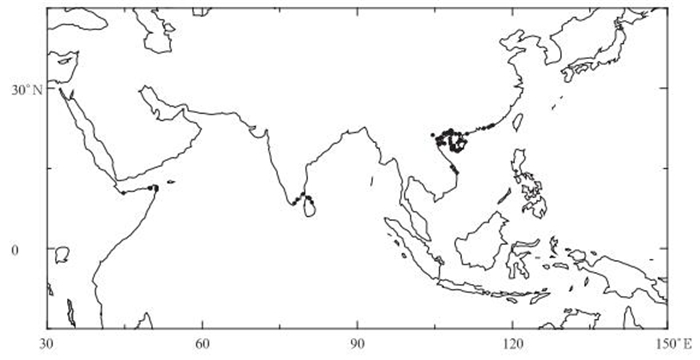
选取全球分布的60个地面控制点如图 7所示。分析得出最初的MERSI遥感图像地理定位结果在扫描方向存在约1.6 km的偏差，在卫星轨迹方向存在约0.3 km的偏差。

图 7

图 7. 地面控制点分布图 Fig 7. Global distribution of 60 ground control points (GCPs)

对于这种现象，可以认为仪器在指向上存在一定偏差。而仪器滚动角和俯仰角的偏差是会分别导致在轨迹和跨轨方向的地理定位误差。所以将滚动角修正0.1034°，同时将俯仰角修正-0.0209°，通过更新仪器安装矩阵，遥感图像重定位结果如图 4b、图 5b、图 6b所示。

由图 4b、图 5b、图 6b可见，经过仪器指向角度的修正后，MERSI遥感图像地理定位结果与真实遥感图像匹配的很好。通过地面控制点分析，经过参数更新后的遥感图像地理定位结果，在扫描方向平均误差为167 m，跨轨方向平均误差为58 m，如表 2所示。MODIS经过首次参数修正后遥感图像地理定位结果在扫描方向平均误差为19 m，跨轨方向平均误差为116 m。可见，利用本方法对MERSI遥感图像地理定位的精度优于一个250 m空间分辨率像元。

表 2

表 2 利用地面控制点的误差分析 Table 2 Ground control point residuals measured before and after updates to the sensor interior orientation parameters 测量 地面控制点个数 扫描方向定位误差/m 跨轨方向定位误差/m 平均值 标准偏差 平均值 标准偏差 首次 60 1670 454 304 316 更新后 60 167 343 58 327

表 2 利用地面控制点的误差分析 Table 2 Ground control point residuals measured before and after updates to the sensor interior orientation parameters

FY-3A MERSI遥感图像地理定位方法包括卫星轨道计算、仪器观测几何建模以及图像地理定位方法。根据MERSI仪器观测特性及其空间位置和指向，建立了观测像元与地面观测位置之间的模型，通过一套完整的坐标系和时间系统转换，完成MERSI遥感图像地理定位计算，并通过地形校正消除地形起伏带来的定位误差。在MERSI在轨运行期间，通过地面控制点分析，修正了MERSI的仪器指向角度，MERSI遥感图像 (250 m分辨率) 地理定位的精度达到像元级。

在今后的工作中，更多的GCP数据将被用来进一步分析和减小MERSI遥感图像地理定位的误差，由于每日以及季节变化所带来的卫星外部环境改变而造成的遥感图像地理定位误差也将被研究。本方法也同样适用于其他“45°扫描镜+多元并扫”的遥感仪器图像地理定位。