应用气象学报  2012, 23 (4): 505-512   PDF    
引用本文
王炳忠, 申彦波. 自然环境条件对太阳能资源计算影响的再思考[J]. 应用气象学报, 2012, 23(4): 505-512.
Wang Bingzhong, Shen Yanbo. Reconsideration About Effects of Natural Environmental Conditions on the Calculation of Solar Energy Resources in China[J]. Journal of Applied Meteorological Science, 2012, 23(4): 505-512  
自然环境条件对太阳能资源计算影响的再思考
王炳忠1, 申彦波2     
1. 中国气象科学研究院, 北京 100081;
2. 中国气象局风能太阳能资源评估中心，北京 100081
2011-09-20 收到, 2012-05-29 收到修改稿.
资助项目: 公益性行业 (气象) 科研专项“太阳能预报技术研究”(GYHY201006036)    
通讯作者: 王炳忠, E-mail: wangbz@cams.cma.gov.cn.
摘要: 文章简单回顾了以前国内常用的太阳辐射资源的计算方法，评论了各自存在的主要问题。其中最重要的是我国大地势以及其他自然条件影响下的基础辐射问题。在以前的研究中虽也注意到了这一问题，但解决得既不理想，也不彻底。关键是这些解决方法依靠的仅仅是辐射实测站点的天文辐射数据。由于测站有限，直接影响到对不同经度、纬度、地势、气候等自然条件下的基础数据的推算。该文利用SMARTS模式依据每个气象站的平均气压、绝对湿度、能见度等数据推算出符合当地环境条件的晴天辐射数据，作为基础辐射数据，进而达到考虑各地真实大气条件来计算晴天辐射的目的。
关键词: 辐射资源计算    SMARTS模式    晴天辐射    
Reconsideration About Effects of Natural Environmental Conditions on the Calculation of Solar Energy Resources in China
Wang Bingzhong1, Shen Yanbo2     
1. Chinese Academy of Meteorological Sciences, Beijing 100081;
2. Center for Wind and Solar Energy Resources Assessment, CMA, Beijing 100081
Abstract: In the calculation of solar energy resources, Ångström method, by means of the sunshine percentage is most commonly used. But it should be noted that this method is suitable for regions where the natural environment is relatively homogeneous. Such conditions are easy to get to meet for small countries or regions. However, for the large countries, e.g., China, it is inappropriate to make an assumption that the natural environment is homogeneous. On one hand, the impact of the terrain on radiation can't be ignored; on the other hand, other atmospheric factors that affect the radiation incident, such as the layer of atmospheric water content, content of aerosol particles and so on, also can't be ignored. Former Soviet Union is also a vast country, and its scholars exclude regions where the altitude is higher than 1500 m when they are dealing with the terrain effect. This approach doesn't resolve the radiation distribution in the mountain area, but from a scientific perspective, it is prudent and rigorous. In the previous researches, the selection of the basic radiation, such as extraterrestrial radiation, clear radiation has been paid more attentions to. This is very important for the Ångström method; however, it doesn't consider the former facts influencing solar radiation enough. The clear radiation close to the actual conditions is calculated based on SMARTS model from Gueymard. In SMARTS model, each factor influencing solar radiation is considered, such as the whole layer water content deduced by surface water content, the aerosol effect considered by horizontal visibility, and the ozone effect derived by ozone content distribution. The clear radiation calculated in this way can be used as basic radiation, which helps overcome the lack of previous work ignoring the atmospheric impact factor. Owing to lack of observation data, the clear radiation in the whole country is not calculated. Only the clear radiation at Chengdu Station and Emei Mount Station are calculated. With the previous method, the results are much the same for two stations, but with the new method, the differences are quite obvious.
Key words: solar resource calculation     SMARTS model     clear radiation    
引言

目前，一些省或地区在研究、讨论当地的太阳辐射资源时，普遍采用的方法就是所谓的Ångström模式，即

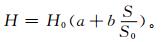
(1)

式 (1) 中, S为某地某时段的实照时数，S0为该时段的可照时数，两者的比值称该时段的日照百分率，H0为大气上界该时段的太阳辐照量 (俗称天文辐照量)，H为欲求出的该时段的地面太阳辐照量, a, b为回归系数。该方法在20世纪初已被提出，前苏联学者对类似的模式作过多方面的研究，详细内容参见文献[1]；我国的一些学者在20世纪60—80年代也先后予以采用, 并对其进行研究和改进。翁笃鸣[2]、高国栋等[3]分别对相关项目进行了大量研究，翁笃鸣曾指出：现有的各种辐射气候计算公式一般具有经验或纯经验的性质。为保证公式的普适性和生命力，应尽可能使之具有充分的物理意义。所以在研制辐射气候计算公式时，应尽可能使之具有充分的物理意义，切忌单纯追求经验式统计拟合的高精度，而忽视公式结构的合理性[2]。

不过，近年来的工作却一直未有改进[4-5]。那么该方法是否就已达到完美境地而无需再改进了呢？它还存在哪些问题？有无进一步的解决方法？对这些问题进行一些思考并作出解答，就是本文的目的。

1 Ångström方法在具体应用中的问题

前苏联运用该方法计算太阳辐射资源的过程是有条件的，就是将1500 m以上的山区，采用斜线将其标识出来，也就是说，计算的结果中，不包括山区部分。应当说，这种态度是严谨和科学的，因为海拔高度的影响在Ångström公式中无法体现。但是如果我国也采用类似的方法来处理，则有些省份根本无法绘制辐射资源图，对于全国也会变得相当破碎。但不应否认，海拔高度的影响客观存在。海拔高度对太阳辐射的影响从我国青藏高原地区可清晰地看到[6]。

2 已有的改进 2.1 传统方法上的改进

在前苏联曾有学者提出使用实际晴天总日射辐照量代替天文辐照量，认为这样更能接近实际[7]。不过，这样的方法要求对已有的辐射测量数据进行处理，并绘出其所有极值的外廓线。这样做不仅工作量大，而且有较多误差。特别是对于我国海拔高的地区地域辽阔，日射站点相对稀疏，若采用上述方法往往海拔高度和纬度不可兼顾，实际上该方法无法应用。

在前苏联还有学者主张采用云量代替日照，而两者之间并非呈线性关系。另外，云量的日观测次数通常为4次，夜间的1次对于日射没有作用，需将其删除，这就要求将各站有关云量的数据重新统计整理，其工作量可想而知。另外3个时刻的观测，没有连续记录的日照计得到的数据连贯、准确，所以也未获广泛认可。

20世纪70年代末，王炳忠等[8]曾提出利用理想大气总日射辐照量代替天文辐照量作为计算的基础辐射量。例如，峨眉山气象站海拔3050 m，而峨嵋市气象站海拔不到500 m，也就是说，两个站以上的气柱厚度相差了近1/3，在计算中不能忽视。这种无形的影响在地形复杂区域无处不在，只是相差的数值不同而已，但这是使用天文辐射所不能反映出来的。理想大气恰好兼有两个优点：既可以直接计算，也可得到任意海拔高度和纬度组合点的辐照量。但更重要的一点是想分担一下系数b所承担的“责任”，因为所有影响太阳辐射的大气因子，均经由系数b来表达。另外，通过对不同海拔高度各站的系数b的研究发现，它与当地的平均绝对湿度 (Wn) 的倒数，存在良好的线性关系，其经验公式为

(2)

从而开启了将整层大气含水量引入辐射计算阶段，尽管思路上具有一定的新意，但在具体实践中，限于当时的计算条件，对于每个计算的站点，在应用经验公式具体计算每个站的辐照量时，本应按其经纬度和海拔高度计算相应时段理想大气的辐照量值代入，实际并未做到，所以失去了原有的设想。另外，由于是理想大气，不同海拔高度上的差异仅限于大气分子的散射和吸收，即使有差异，也并不显著，这也为祝昌汉的工作所证实[9]。

2.2 地形对辐射影响

地形影响方面，研究方法可分为几何法和地理信息系统 (DIS) 法两种。

几何法早在20世纪50年代就有前苏联康德拉捷夫进行过较系统的研究[1]，我国则由傅抱璞发端[10-11]，其后则有李占清等[12-13]。这类研究主要是将不同的坡面及其朝向当作几何面，运用几何等数学方法来处理丘陵坡地，实际并不涉及高差达千米以上的、地貌极其复杂的高山、峡谷等地势。

在利用网格点数字高程数据方面又有两种截然不同的处理方法：

① 认为在地表平坦、大气为水平均一的假定条件下，可以将地面站点的测量向二维空间外推。但当地表不均一或崎岖不平时，就很难进行外推[14]。于是利用卫星资料和地形结合大气辐射传输模式或野外观测，并考虑地形参数，如坡度、坡向、高度、天空视角计算其影响的方法计算地表辐射。其研究目的是要回答应用中分辨卫星资料计算地表净辐射是否需要考虑地形影响，不考虑会产生多大误差。研究采用的是美国地质调查中心发布的GTOPO30全球数字高程数据，经纬度分辨率为30″，海拔高度误差为±30 m。结果表明，地形作用产生的相对辐射误差可达20%。

② 利用起伏地形下天文辐射分布式计算模型，以1 km×1 km分辨率的数字高程模型 (DEM) 数据作为地形综合反映，借助地理信息系统ARCGIS 8.1获得各网格点的坡度、坡向、纬度和高程信息，计算出各网格点受地形影响后的可照时数及相应的日照百分率，继而根据天文日辐照量H0计算各点受地形影响下的日天文辐照量H0αβ[15]，并利用下式作为推导出各种起伏地形下的各种辐射成分的辐照量：

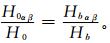
(3)

式 (3) 中, Hb为水平面辐照量，而Hbαβ为起伏地形下的辐照量[16]。

式 (3) 看似合理，实际上概念已被置换。表面上它适用于任意地形和海拔高度，因为任何有大气影响的成分放在式 (3) 的分子和分母上均可自动抵消掉，但其前提是Hb和Hbαβ是在同一大气条件下。因为根据Bouguer-Lambert定律，在不考虑光谱量的前提下，大气对入射辐射的衰减可写作

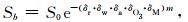
(4)

式 (4) 中, S0为太阳常数，Sb为到达地面的辐照度，δ称光学厚度，其下标含义：r为气体分子，O3为臭氧，a为气溶胶，w为水汽，M为NO, CO2等，m为大气质量。后者的计算式为

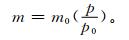
(5)

式 (5) 中, p为站点气压，p0为标准气压，m0为标准气压下的大气质量。由此可知，式 (3) 中等号右侧分子和分母中的气压若不相等，则该等式不能成立；或者要求Hbαβ和Hb是在相同的大气条件下测得。另外，无大气则无散射，不能将在无大气得到的关系用于有大气的情况。这些均证明式 (3) 不能解决本研究所设定的问题。

不过，这种做法却有日渐普及之势[17-18]，有的甚至将其应用到100 m×100 m[19]，90 m×90 m[20]网格，似乎没有前提条件，只要有足够细致的地理信息就可以使用。这里需要强调几点：① 式 (3) 成立是有条件的，仅适用于较小的地域范围内和高差不大的情况下；② 宏观尺度的辐射分布问题，尚未得到较为满意的解决，不宜在此基础上作进一步细化工作；③ 网格不可随意增加密度，其间的物理机制必须清楚，否则会将大气候与小气候混淆，如果用国内百多个辐射站这种过于宏观尺度的数据，就能解决100 m×100 m尺度的气候问题，国内则无需设立两千多个气象站和更多的自动气象站了。

3 大范围地势的影响 3.1 过去工作的简单回顾

左大康是我国研究太阳辐射的先驱之一[21]，他所采用的H0是晴天辐射，为了解决晴天辐射数据不足，他使用的是晴天辐射纬度平均值。这样不能反映H0对海拔高度依赖关系。

钟强在解决青藏高原总辐射计算中[22]，同样强调H0的作用十分重要，为了解决海拔高度的影响，利用青藏高原及其周围共6个站点的辐射数据，用最小二乘法得出与太阳高度的经验关系式：

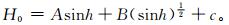
(6)

显然，仅靠太阳高度角h来解决整个青藏高原晴天辐射是远远不够的，尽管其相关系数高达0.98~0.99。因为仅靠太阳高度角解决不了不同地点由于气压、水汽和气溶胶不同所引起的辐射差异。c为回归系数。

翁笃鸣十分重视总日射计算中的起始数据问题[2]，也就是式 (1) 中的H0，并认为取天文辐射 (HT，0) 为第1近似，理想大气辐射 (HL, 0) 为第2近似，晴天辐射 (HQ, 0) 为第3近似。在晴天总日射的计算中，他所依据的是前苏联М Е Берлянд的理论方法。具体地讲，该理论由下式表示：

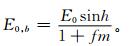
(7)

式 (7) 中, h为太阳高度角，m为大气质量，f为Берлянд根据散射理论得出的系数。

仅从式 (7) 的外观来看，该理论与Bouguer-Lambert定律相比就显得过于简单。除了m可以反映气柱的影响外，其他大气中成分的变化仅靠f来体现，是难以成立的。由于该理论系20世纪50年代的研究成果，与大气科学理论发展现状难以匹配，因此，该方法是不够准确和难以胜任的[23-24]。

3.2 新思路

目前研究工作的基点仍然是Ångström公式，认为它所能解决的仅仅是云量对辐射的影响，并且认同起始数据H0是辐射计算中的首要参数的提法。这里所谓的新思路就是提出全面考虑影响太阳辐射到达地面各种因素的H0计算方法。

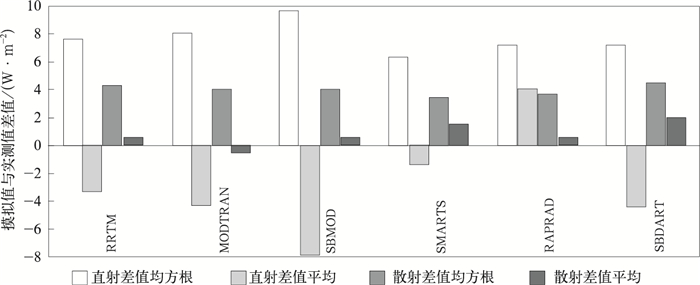
本研究所依据的是Gueymard研制的SMARTS模式[25]。该模式曾在一次数种辐射模式 (包括MODTRON5) 对同一时段实测参数的对比试验中，具有不俗的表现[26]，其效果甚至不比著名的MODTRAN模式差 (图 1)。该模式可以在网站上注册后自由下载，为了便于国内用户使用，在参考各种相关文献以及使用心得的基础上，编写出版了文献[27]，可供参阅。

图 1. 各种模式模拟与测量结果差值的统计[26] Fig 1. Differences between simulation results from six models and measurement results[26]

模式具体使用方法不再赘述，仅对如何获取一些重要的大气参数作讨论，这样才可以具体应用SMARTS模式。下面仅就Bouguer-Lambert定律式 (4) 中的各变量的选取进行介绍。由于需要计算的对象是每个感兴趣的气象站 (不仅是辐射站)，这里对各站具体参数的确定方法进行介绍。

① 臭氧 根据美国NASA公布的全球范围内逐日臭氧数据 (2005—2009年)[28]，经统计和处理我国经纬度范围内的数据，绘成各月臭氧经纬网格分布图。当然，由于臭氧只影响太阳辐射的紫外部分，对于总日射的实际影响，微乎其微，可不考虑；但对于紫外辐射，则是必不可少的输入参数之一，图 2仅以1月为例。

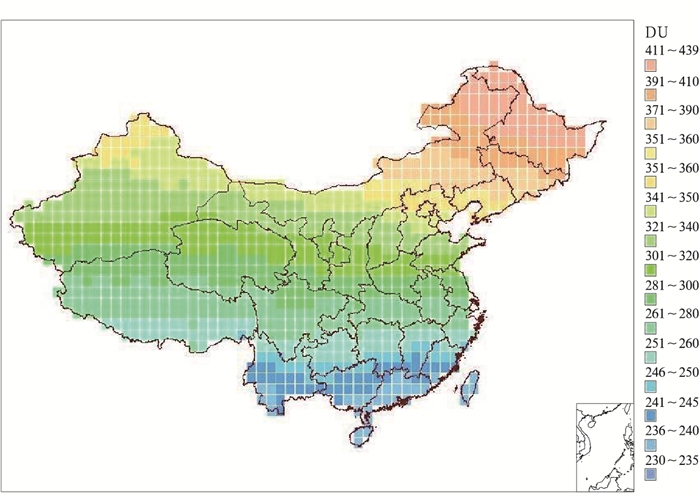
图 2. 2005—2009年1月我国的臭氧分布 Fig 2. Distribution of O3 over China in January during 2005—2009

② 气柱厚度 (反映当地海拔高度) 及气体成分 可用当地月平均气压值输入。

③ 气溶胶 由于模式本身已建立各种气溶胶参数之间的相互内在联系，可以在Ångström混浊系数β(1000 nm处以自然对数表示的气溶胶光学厚度AOD)、Schüepp混浊系数B(500 nm处以常用对数表示的AOD)、TAU550(550 nm处的AOD)、VR(以Koschmieder方程为基础的气象视距) 和VISI (能见度) 之间任意选择一种。根据我国具体情况，建议选择月能见度平均值输入。上述各参数之间的关系详见文献[27]。

④ 水汽含量 从历史经验看，从事太阳辐射研究最终必然要研究整层大气水汽含量的计算，因为它对辐射的吸收不能忽略。20世纪80年代孙治安[29]就曾研究过这一问题，后来很多人也曾从事这方面的研究[30-32]，国外的相应文献可参阅[33-34]。对于上述各种方法之优劣，这里不作评述。需要指出的是，上述国内文献大多着眼于全国，国外文献也有其地域局限性，各地可以参考具体思路，根据本地区内探空站的数据，另行拟定当地的公式为宜，切忌照搬经验公式。

将各种参数确切的数值代入模式，就可以计算出当地的晴天辐射 (其中包括法向直射，水平面的直射、散射和总日射等)。计算需要逐日进行，据模式编制者建议，为了得到较好的准确度，使用积分时间步长应不大于6 min；为了快速得到结果，则建议使用积分时间步长应不小于15 min。

4 计算实例

欲通过利用本文所介绍的方法直接计算出全国的辐射分布来是不现实的，因为臭氧、水汽含量、气溶胶等各项具体参数，本研究所提供的仅仅是一种可能性。全面研究各种参数的全国分布，本身就是一项内容浩大的工程。为了避免空泛的说教，特将峨眉山气象站与成都气象站采用所介绍方法的计算情况作一对比。

表 1是为了计算所准备的两站各项原始数据。其中整层水汽是依据成都站1971—2000年的多年平均数据计算得到。其余参数除能见度为1981—2000年的平均值外，各参数的年限与探空数据相同。至于峨眉山站的整层水汽，由于该站没有探空观测，鉴于当地气压接近700 hPa，且距成都站的直线距离约120 km，考虑直接采用成都站750 hPa以上的水汽来代表。因为在700 hPa以上的高空，水汽的水平方向变化不会过于剧烈。表 2中列举了两站晴天辐射的计算结果，同时还列出了利用SMARTS程序计算的天文辐射。

表 1 SMARTS程序所必需输入的计算参数 Table 1 The necessary input parameters for SMARTS model

表 2 成都站、峨眉山站晴天辐射和天文辐射计算结果 (单位：MJ/m2) Table 2 The calculated clear solar radiation and extraterrestrial solar radiation at Chengdu Station and Emei Mount Station (unit: MJ/m2)

将表 1中的参数输入到SMARTS程序中，并取3 min为间隔计算1次，由日出至日落。从输出结果中选取如下3种数据：当次的太阳天顶角 (Z)、地外太阳常数 (CT)(已经日地距离订正) 和总日射辐照度 (Eg)。计算cosZ×CT得到水平面上的天文辐射；并对每次计算的cosZ×CT和Eg进行累计；最后，对其乘180 s/1000000，将单位换算成MJ/m2。

通过比较表 2中天文辐射和地面辐射的数据，不难看出两地的天文辐射相差并不多 (10 MJ/m2以内)，因为天文辐射只是地理纬度的函数，纬度差异不大，结果自然也不会大。但是，推荐方法计算的地面晴天辐射相差则较大 (150~300 MJ/m2)。这必然会直接影响最后的计算结果。式 (1) 中的[a+b×(S/S0)]的含义，特别是系数a和b，对于天文辐射 (HT, 0) 和晴天辐射 (HQ, 0) 来说是绝然不同的。对于前者，大气中所有影响辐射透射的因子必然均涵盖其中 (可以说是不堪重负)；对于后者，由于各种影响辐射透射的参数均已在计算HQ, 0过程中予以考虑，其所承担的“任务”就会简单得多。对于任何一个已知站点，[a+b(S/S0)]就是一个定值。关键在于H0值，H0值大，计算的H值必然大；反之亦然。所以利用天文辐射来解决山地的辐射计算问题，是难于获得圆满结果的。文献[35]中指出，分区公式计算的最大误差为19.30%，全国公式计算的最大误差为18.75%，均为峨眉山站，即各公式对山地太阳辐射计算效果较差。不过，应当承认推荐的方法从物理角度讲更合理，但其计算量过大，所需基础性工作 (如整层水汽含量的推算) 较重，是其不足之处。

5 小结

本文的目的不在于全面论述有关辐射资源的计算方法，仅着眼于与Ångström公式有关的一些问题，因其应用范围最广，且已成为气象行业标准[36]。Ångström公式确实是一个计算太阳辐射的好方法，但其具体应用仅限于解决天空遮蔽条件。Ångström公式兴起于欧洲国家，由于这些国家地域范围不大 (或者像前苏联将海拔高度大于1500 m的山区排除在外)，用于辐射计算未遇见大的困难。但对于我国则不然，地势问题无法回避，这也是多年以来一直努力研究的方向。从3.2节的介绍可知，尽管云量对日射的影响是第1位的，但是，对于具有世界第3极之称的青藏高原以及纵跨约40°纬距的我国来说，水汽、气溶胶的影响也不容忽视。天文辐射计算起来，十分简单、方便，但仅靠a和b两个系数无从表达如此众多变量，可以说a和b系数负担过重。

H0的重要性也逐渐被人们所认识，但解决起来却不容易。天文辐射 (HT, 0) 最简便，但距离实际相差太远；晴天辐射 (HQ, 0) 的优越性显而易见，但辐射站的数量有限。理想大气辐射 (HL, 0) 可以计算任意经纬度点的数据，但仅限于考虑大气分子部分，真正变化大的水汽、气溶胶并未考虑到，所以也不成功。这也正是本文解决的重点。虽然本研究仍计算晴天辐射，但它有别于以往的、仅依实测数据推导出的晴天辐射，并可以依据任何地点一般气象数据推算出来，因此可以称之为当地的气候晴天辐射。

应当承认，要具体实践这种方法的工作量巨大，不过对于计算技术已高度发展的今天，这不应成为问题。本文提出的方法虽好，但仅依靠作者力量完成全国范围内的细致分布图，仍力不从心。假如仅计算部分站点，侧绘出的晴天辐射全国分布图在外观上与过去的不会有重大差别：依然是青藏高原地区最高，新疆次之，四川最低，这是由这些地区的实测数据决定的。重要的是本方法在内在结构和物理机制上更为细致、合理。可以设想，如果在省及地区范围内使用本方法，且站点足够多，分布细节上一定会有所改观。

不过，作为方法研究是不尚空谈的，作者曾应用该模式计算研究了我国各纬度太阳能利用的最佳倾角问题[37]。更多的使用实例，还可参阅文献[27]的第4章。其差别仅是输入的参数不同而已。

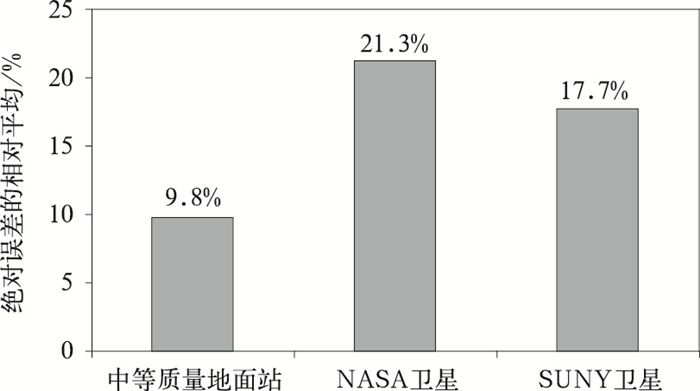
目前国际上绘制辐射资源图普遍采用的方法是利用卫星提供的信息。但据最近美国的研究报道，卫星方法结果的误差普遍较大，约为±20%，而利用站点数据，既使是比较简易的光电仪器，其误差也不超过±10%(图 3)[38]。看来增加简易站点，仍是一条有效的途径。

图 3. 各种日总辐射值的平均误差[38] Fig 3. Mean Errors of several daily global radiation values[38]

致谢 在臭氧数据统计和绘图方面分别得到中国气象局气象探测中心丁蕾硕士和边泽强博士的协助，谨表谢忱。
参考文献
[1] Кандратьев К Я Лучистая энергия солца. 太阳辐射能. 李怀瑾, 译. 北京: 科学出版社, 1962.
[2] 翁笃鸣. 中国辐射气候. 北京: 气象出版社, 1997.
[3] 高国栋, 陆渝蓉. 中国地表面辐射平衡与热量平衡. 北京: 科学出版社, 1982.
[4] 张运林, 秦伯强, 陈伟民, 等. 太湖无锡地区太阳总辐射的气候学计算及特征分析. 应用气象学报, 2003, 14, (3): 339–347.
[5] 杨羡敏, 曾燕, 邱新法, 等. 1960—2000年黄河流域太阳总辐射气候变化规律研究. 应用气象学报, 2005, 16, (2): 243–248. DOI:10.11898/1001-7313.20050230
[6]
[7] Барашкова Е П и др. Радиационный рецим территории СССР. Гидрометиздат, 1961.
[8] 王炳忠, 张富国, 李立贤. 我国的太阳能资源及其计算. 太阳能学报, 1980, 1, (1): 1–9.
[9] 祝昌汉. 再论总辐射计算方法 (二). 南京气象学院学报, 1982, 2, (2): 196–206.
[10] 傅抱璞. 论坡地上的太阳辐射总量. 南京大学学报:自然科学, 1958, (2): 47–82.
[11] 傅抱璞. 实际地形中辐射平衡各分量的计算. 气象学报, 1964, 34, (1): 62–73. DOI:10.11676/qxxb1964.007
[12] 李占清, 翁笃鸣. 一个计算山地地形参数的计算机模式. 地理学报, 1987, 42, (3): 269–278.
[13] 李占清, 翁笃鸣. 坡面散射辐射的分布特征及其计算模式. 气象学报, 1988, 46, (3): 349–356. DOI:10.11676/qxxb1988.043
[14] 王开存, 周秀骥, 刘晶淼. 复杂地形对计算地表太阳短波辐射的影响. 大气科学, 2004, 28, (4): 625–633.
[15] 曾燕, 邱新法, 刘昌明, 等. 基于DEM的黄河流域天文辐射空间分布. 地理学报, 2003, 58, (6): 810–816. DOI:10.11821/xb200306002
[16] 曾燕, 邱新法, 刘昌明, 等. 起伏地形下黄河流域太阳直接辐射分布式模拟. 地理学报, 2005, 60, (4): 680–688. DOI:10.11821/xb200504017
[17] 李梦洁, 郑建飞, 曾燕, 等. 浙江省高分辨率太阳直接辐射图的计算和绘制. 地球科学进展, 2008, 23, (3): 299–305.
[18] 姜创业, 王娟敏, 孙娴, 等. 陕西省山地太阳总辐射分布式模拟研究. 地理与地理信息科学, 2010, 26, (3): 91–94.
[19] 袁淑杰, 缪启龙, 谷晓平, 等. 贵州高原起伏地形下太阳直接辐射的精细分布. 自然资源学报, 2009, 24, (8): 1432–1439. DOI:10.11849/zrzyxb.2009.08.012
[20] 武永利, 张洪涛, 田国珍, 等. 复杂地形下山西高原太阳潜在总辐射时空分布特征. 气象, 2009, 35, (5): 74–82. DOI:10.7519/j.issn.1000-0526.2009.05.011
[21] 左大康, 王勃贤, 陈建绥. 中国地区太阳总辐射的时空分布特征. 气象学报, 1963, 33, (1): 78–96. DOI:10.11676/qxxb1963.007
[22] 钟强. 青藏高原太阳总辐射的计算方法讨论. 高原气象, 1986, 5, (3): 197–210.
[23] 孙治安, 高庆先, 史兵, 等. 中国可能太阳总辐射的气候计算及其分布特征. 太阳能学报, 1988, 9, (1): 12–23.
[24] 翁笃鸣, 高歌. 晴天太阳总辐射的一种参数化形式. 南京气象学院院报, 1995, 18, (3): 317–323.
[25] Gueymard C. SMARTS, A Simple Model of the Atmospheric Precipitable Water and Transfer of Sunshine: Algorithms and Performance Assessment. Professional Paper FSEC-PF-270-95. Florida Solar Energy Center.
[26] Michalsky J J. Shortwave radiation closure studies for clear skies during the atmospheric radiation measurement 2003 aerosol intensive observation period. J Geophys Res, 2006, 111: D14S90.
[27] 王炳忠, 申彦波. 使用太阳能光谱应用模式——SMARTS模式. 北京: 气象出版社, 2011.
[28] [2011-08-02]. http://ozoneaq.gfsc.nasa.gov/OMIOzone.md.
[29] 孙治安. 我国平均水汽含量含量的气候计算及其时空分布特征. 南京气象学院院报, 1987, 10, (1): 74–80.
[30] 王炳忠, 刘庚山. 我国大陆大气水汽含量的计算. 地理学报, 1993, 48, (3): 244–253.
[31] 杨景梅, 邱金桓. 我国可降水量同地面水汽压关系的经验表达式. 大气科学, 1996, 20, (5): 620–626.
[32] 杨景梅, 邱金桓. 用地面湿度参数计算我国整层大气可降水量及有效水汽含量方法的研究. 大气科学, 2002, 26, (1): 9–22.
[33] Muhammad Iqbal. An Introduction to Solar Radiation. New York: Academic Press, 1983.
[34] Gueymard C. Analysis of monthly average atmospheric precipitable water and turbidity in Canada and Northern United States. Solar Energy, 1994, 53, (1): 57–71. DOI:10.1016/S0038-092X(94)90606-8
[35] 和清华, 谢云. 我国太阳总辐射气候学计算方法研究. 自然资源学报, 2010, 25, (2): 308–319. DOI:10.11849/zrzyxb.2010.02.015
[36] 中华人民共和国气象行业标准QX/T89-2008. 太阳能资源评估方法. 北京: 气象出版社, 2008.
[37] 王炳忠, 申彦波. 从资源角度对太阳能装置最佳倾角的讨论. 太阳能, 2010, (7): 17–20.
[38] Hall James, Hall Jeffrey. Quality Analysis of Global Horizontal Irradiance Data from 3500 US Ground-based Weather Stations. [2011-08-02]. http://www.solardatawarehouse.com/data.aspx#Technical_Papers/.