山基GPS掩星大气探测技术是在山顶上架设GPS接收机,用来探测特定区域气象数据的一种新技术,该技术主要用于获取从地面至接收机所在高度的大气参数的垂直分布信息,最多延伸到接收机以上高度1~2 km。山基GPS掩星大气探测最先由Meehan等[1]提出,并尝试了山基掩星观测实验。Zuffada等[2]随后又进行了山基掩星的数值模拟试验。Mousa[3]和Aoyama等[4]对2001年和2002年在日本富士山顶进行的两次山基GPS掩星观测试验数据进行分析,目的是验证山基掩星反演方法的可行性,获得了一些有益的经验和结果。国内张训械等[5]也曾开展过山基掩星观测的模拟研究,胡雄等将观测数据的反演结果与模拟结果进行过比较分析,获得了较好的结果[6-8],还有研究对山基掩星数据反演误差也进行了分析[9-11]。
山基掩星探测的高度范围全部处于低对流层区域,水汽含量特别丰富,且变化迅速,使得接收机无法跟踪掩星信号。尤其是由于水汽含量在垂直方向上的剧烈变化产生的大气多路径效应,影响更为严重。本文提出采用全谱反演方法来处理山基掩星数据,以抑制在低对流层区域由多路径效应引起的误差。采用全谱反演技术处理掩星数据来抑制多路径误差最先是由Jensen等[12]提出,并讨论了将该方法应用于理想掩星数据和实际掩星数据处理的不同,并用于模拟掩星信号的数据反演,验证反演方法的可行性;国内胡雄等[13]采用全谱反演方法处理15 km以下掩星数据反演,成功获得了大气折射率剖面。
本文首次将全谱反演技术应用于低对流层 (地面至接收机所在高度或其上1~2 km范围) 的掩星数据处理,并将处理结果与几何光学反演结果以及时空匹配的实测探空数据进行比对,并对结果进行了误差分析。
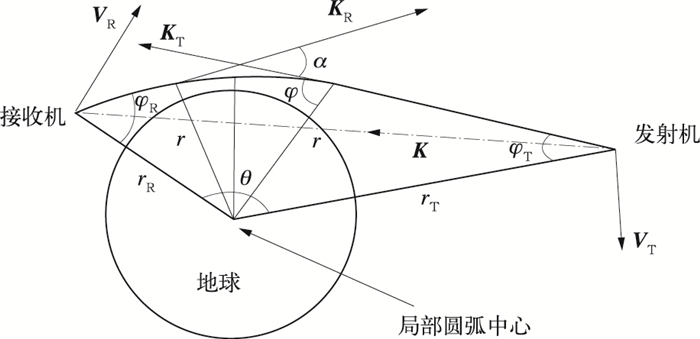
1 反演方法 1.1 山基掩星数据几何光学反演方法山基GPS掩星观测几何示意图如图 1所示,接收机位于山顶,发射机位于GPS卫星上。由于大气的折射作用,穿越大气的电波信号发生弯曲。假设地球大气为球对称球面分层结构,在球对称介质中传播的信号的弯曲角可表示为[14-15]
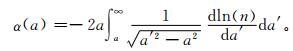
|
(1) |
|
|
| 图 1. 山基GPS掩星观测几何示意图[13] Fig 1. Geometric diagram of the mountain-based GPS radio observation of occultation[13] | |
式 (1) 中,α为信号传播的弯曲角;a为射线的碰撞参数;r是从对称原点到射线路径上某一点的距离;n是r距离处的折射指数;且a′=nr, 表示积分路径上的碰撞参数。
由于受到大气延迟作用,GPS载波信号的多普勒频移可表示为
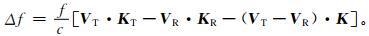
|
(2) |
式 (2) 中,f为GPS信号发射频率;c为光速;VT和VR分别为发射机和接收机的运动速度;KT和KR分别为发射机与接收机的信号传播方向的单位矢量;K为连线方向的单位矢量,由发射机指向接收机。对山基掩星观测,接收机位置固定,VR的大小为0。根据图 1中的几何关系,弯曲角可表示为
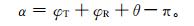
|
(3) |
式 (3) 中, φT表示对称原点与发射机连线同发射机信号传递方向的夹角,φR表示对称原点与接收机连线同接收机信号传播方向的夹角,θ表示对称原点分别与接收机和发射机连线之间的夹角。
从卫星星历获得发射机位置和速度,结合多普勒频移公式和掩星的几何关系,就可获得弯曲角随碰撞参数的变化α(a),将其作为反演的输入量,对式 (1) 进行Abel积分变换,能获得大气折射指数表达式[9, 13]:
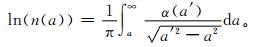
|
(4) |
注意到式 (4) 的积分上限为∞,当接收机位于大气层内距对称原点为rR处时 (如在一个山顶上),只能获得a<rRn(rR) 时的α(a) 测量值。这里引入一个新的变量,即局部弯曲角α′(a),它等于对应碰撞参数为a时负仰角测量时的弯曲角αN与同一碰撞参数对应的正仰角测量时的弯曲角αP之差[3]。它只存在于接收机高度以下路径部分,且当接近接收机位置时其值趋近于0,即
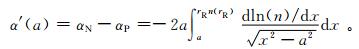
|
(5) |
式 (5) 中,x=nr,rR指接收机所在位置至对称原点的距离,n(rR) 表示rR高度处的折射指数,积分上限为接收机所在高度处。式 (5) 经Abel积分变换可以得出大气的折射指数廓线表达式:
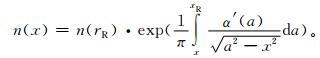
|
(6) |
式 (6) 中,n(rR) 为接收机所在位置高度的大气折射指数,由式 (6) 即可获得相应高度的大气折射率。
1.2 山基掩星数据全谱反演技术由于受多路径效应的影响,会存在不同时刻的掩星信号同时到达接收机的情况,从而使得在时域上无法准确获得弯曲角随碰撞参数的变化α(a),为解决这个问题,本文引入全谱反演技术[12]。
全谱反演必须要满足3个条件:① 信号的任何瞬时频率在掩星过程中只发生1次;② 每个子波信号的振幅与其相位相比是缓变的;③ 信号相位的二阶导数远大于其高阶导数。在GPS掩星观测中,全谱反演所需的上述条件基本满足。GPS接收机观测的复信号可以表示为
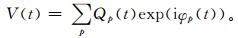
|
(7) |
式 (7) 中,φp宽与Qp分别是第p个子波的相位和振幅,i为虚单位,将式 (7) 进行傅立叶变换,将信号从时域转换到频域,利用稳定相位点法 (MSP)[15]可估计为
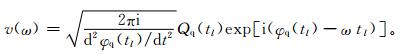
|
(8) |
式 (8) 中,φq表示角频率为ω的子波的相位,tl表示相应于这个子波的瞬时频率为ω的时刻。式 (8) 表明,可以将傅立叶频谱中的不同频率成分看作是信号的瞬时频率,而它们发生的时间可以简单地由傅立叶频谱和相应分量的相位导数给出。
对于GPS掩星观测信号,假设GPS卫星在掩星发生的平面内的圆形轨道运行,大气为球对称,其瞬时多普勒频率为[12]
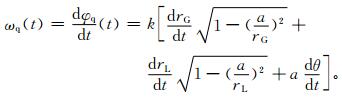
|
(9) |
式 (9) 中,φq是信号相位,k是波数,rL和rG分别是地心到LEO卫星和GPS卫星的距离,a是碰撞参数,θ表示rL和rG之间的夹角。
将θ作为独立变量用来取代时间t,即将式 (9) 对θ求导数,再引入一个相位因子φm(θ),来消除径向变化的影响之后可得[12-13]
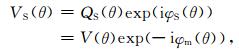
|
(10) |
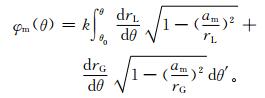
|
(11) |
其中,θ0是初始角度,V(θ) 表示测量复信号对θ的重采样值,VS(θ) 代表信号消除了径向变化引起的频移之后的测量值,am表示碰撞参数先验值,可从平滑的相位数据中获得。φS与QS分别是相应的相位和振幅。
VS的伪频率变化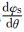
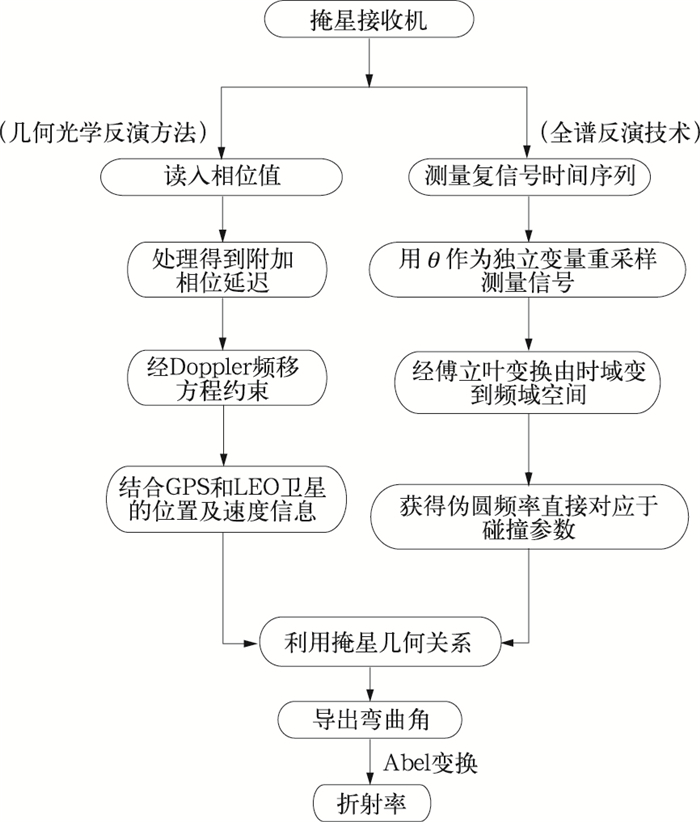
图 2为几何光学反演方法与全谱反演方法的流程图。
|
|
| 图 2. 几何光学反演法与全谱反演技术流程图 Fig 2. Flow chart of Geometric OPtics (GOP) and Full Spectrum Inversion (FSI) methods | |
2 数据处理结果比对
本文利用全谱反演技术,对2005年8月在河北兴隆雾灵山进行的山基掩星观测试验获取的探测数据进行了处理,并将全谱反演结果与几何光学反演结果和同时进行的小球探空结果进行了比对分析。
2.1 数据来源2005年8月,中国气象局在河北兴隆雾灵山组织了山基掩星观测试验。掩星接收机架设在雾灵山顶 (40.51°N,117.41°E,海拔2118 m),接收机天线方向朝向正南。同时在雾灵山东南偏南方向 (相对雾灵山方位角为160°) 直线距离30 km处的兴隆县气象局内 (40.25°N,117.29°E,海拔584 m),还采用59型探空仪和北京大学低空探测系统进行了同步的联合探空观测,获得丰富的探空数据。
试验获取的可用于全谱反演的掩星数据为8月20—26日期间获取的包含了信噪比与振幅信息的掩星数据,同时8月20—26日在兴隆利用低空探测系统进行了19次小球探空,利用59型探空仪进行了8次大球探空,其中同步施放8次,共获得19份独立数据。为了尽可能多地发挥探空数据的价值,在时间匹配方面,以探空时间为标准,选取常规探空过程前后1.5 h之内发生的掩星事件的反演结果来与探空资料进行比对分析;空间匹配原则根据探空站地点相对掩星观测点的方位角 (160°),选取方位角偏差在40°以内的掩星数据来进行比对。
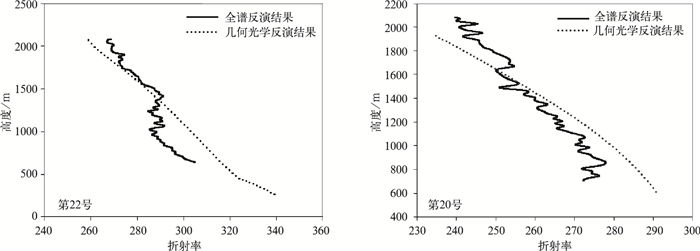
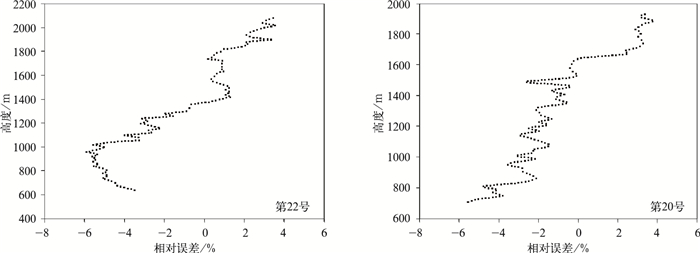
2.2 全谱反演结果与几何光学反演结果的比对利用全谱反演技术对包含信噪比与振幅信息的掩星数据进行处理,获得86条接收机所在高度以下的折射率廓线,将反演结果同利用山基掩星数据几何光学反演方法获得的折射率廓线进行对比分析。图 3所示为2005年8月22日第22号和第20号GPS卫星发生的掩星事件处理结果的比对情况,图 4为其相对误差随高度变化的分布图。从第22号比对图像可以看到,二者在高层的符合精度较好,但对于低层,尤其1300 m以下,全谱反演结果明显偏小,最大负偏差达到6%。就整体而言,二者的变化趋势一致,平均相对偏差为-1.21%,标准偏差为2.99%。第20号比对图像同样也存在越到低层全谱反演结果的负偏差越大的情况,最大负偏差达到了6%。二者的平均偏差为-0.88%,标准偏差为2.49%。
|
|
| 图 3. 全谱反演结果与几何光学反演结果比对情况 Fig 3. Comparison of the refractivity obtained from FSI and GOP | |
|
|
| 图 4. 比对结果相对误差 (相对几何光学反演结果) Fig 4. Relative deviation (comparison to the results obtained from GOP) | |
将8月20—26日获得的86份包含信噪比和相位信息有效数据的物理反演结果同山基掩星数据几何光学反演结果进行比对,发现都有越接近底层负偏差越大的情况,尤其是1000 m以下,偏差更大。经过比较分析发现,二者最大的负偏差达到了6%,但其平均相对偏差保持在2%以内,几何光学反演结果偏大,其相对偏差的标准差低于3%。
2.3 全谱反演结果与常规探空数据的比对 2.3.1 常规探空数据的处理由于受到时间与空间匹配原则的限制,只有6组探空数据有匹配较好的掩星观测数据用于比对分析。用探空数据中的温度信息,利用式 (12) 马格鲁斯经验公式[16]由探空温度计算饱和水汽压:
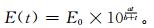
|
(12) |
式 (12) 中,E(t) 为对应温度为t时的饱和水汽压;E0为常数,其值为6.1078 hPa;a,b为常数,对平水面而言,a=7.5,b=237.3℃。对平冰面而言,a=9.5,b=265.5℃。
结合探空资料的相对湿度信息和计算出的饱和水汽压值,可以获得实际水汽压值:
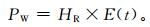
|
(13) |
式 (13) 中,PW为实际水汽压值,HR为相对湿度。
利用折射率与大气参数之间的近似关系就能获得折射率廓线:
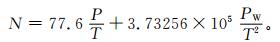
|
(14) |
式 (14) 中,N表示大气折射率;P和PW分别表示大气总压和水汽分压,单位:hPa;T为大气绝对温度,单位:K。
2.3.2 数据处理结果的比对分析利用高度匹配的原则,从全谱反演获取的折射率廓线中随机抽取某一高度对应的折射率数据,与同一高度上由探空获得的折射率信息进行比对分析,计算全谱反演结果与探空结果的相对误差。对随机抽样数据进行统计分析,并计算平均相对误差和标准偏差。每一组匹配数据随机抽取10个不同高度值,6组数据共抽取60个比对样本,通过对6组匹配数据的分析得出:反演结果同探空结果的变化趋势趋于一致,这表明全谱反演技术的应用是成功的,算法和程序均得到了检验。但比对结果还存在偏差,掩星数据全谱反演结果与探空结果相比偏小,最大负偏差达到10%,平均相对偏差为-8.15%,相对偏差的标准偏差为1.4%。误差来源主要有几个方面:① 时空匹配不完全一致带来的误差;② 反演过程中引入的假设条件,如大气局部球对称假设,也将带入一定误差。
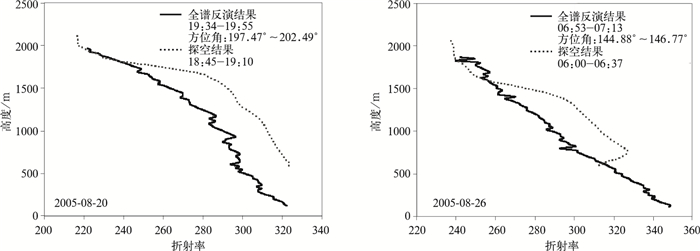
图 5分别是2005年8月20日19:00(北京时,下同) 和8月26日06:00的探空结果与时空匹配的掩星数据全谱反演结果比对图像。从图 5可以看到,二者在顶部符合程度较底部好,1500 m以下偏差比较大,最大偏差达到10%,探空结果偏大,但总体的变化趋势仍趋于一致。这种近地面区域误差要比中间高度偏大情况可能是由Abel积分的边界问题引起,如何减小或消除该项误差还需在以后的工作中探讨与解决。
|
|
| 图 5. 全谱反演结果同探空结果的比对图像 Fig 5. Comparison between the retrieval results from FSI and radiosonde data | |
2.4 与国内外相关研究的对比
国外的相关研究主要是Jensen等将全谱反演技术用于了模拟掩星信号的数据反演[11],并将反演获得弯曲角剖面与从折射率模型利用Abel变换重构的弯曲角剖面进行比对,两者符合较好。
国内胡雄等采用组合反演方法处理掩星数据,15 km以上采用几何光学反演方法处理,15 km以下采用全谱反演方法处理[13],应用于GPS/MET掩星数据和CHAMP掩星数据反演,并与传统几何光学反演结果进行了对比分析,结果表明:全谱反演方法与几何光学反演结果在8~15 km基本一致,在8 km以下反演结果存在一定误差,其最低反演高度为4 km。
本文首次将全谱反演技术应用于低对流层 (地面至接收机所在高度或其上1~2 km范围) 掩星观测数据处理。在这一高度层内,由于水汽含量丰富,掩星信号相对于高层 (8 km以上) 受多路径效应影响非常严重,全谱反演结果与几何光学反演结果存在偏差,是由于在利用几何光学原理反演时,未考虑多路径的影响,而全谱反演能有效去除多路径效应的影响,从而使其反演结果更接近于真实值。
3 结论1) 针对低对流层的多路径问题,首次将全谱反演方法引入到山基GPS掩星观测数据处理中来,并成功获取了大气折射率剖面,与几何光学反演结果基本一致,表明全谱反演方法在山基掩星数据反演中是可行的、有效的反演方法。
2) 将山基掩星观测数据全谱反演结果与几何光学反演结果和联合探空结果进行比对分析,结果表明:全谱反演结果与几何光学反演结果平均相对偏差小于2%,全谱反演结果偏小,标准偏差低于3%;全谱反演结果与联合常规探空结果的平均相对偏差为8.15%,全谱反演结果偏小,标准偏差为1.4%。误差来源包括比对数据时空匹配时带来的误差,反演方法引入的误差,理论上全谱反演能有效去除低对流层多路径效应的影响,从而使其反演结果更接近于真实值。
| [1] | Meehan T K, Kursinski E R, Hajj G A, et al. Analysis of GPS signals occulted by the atmosphere as tracked from mauna Kea using the TurboRogue GPS receiver. Trans Am Geophys Union (EOS), 1991, 72: 372. |
| [2] | Cinzia Z, Hajj G, Robert E K. A novel approach to atmospheric profiling with a mountainbased or airborn GPS receiver. J Geophys Res, 1999, 104, (D20): 24435–24447. DOI:10.1029/1999JD900766 |
| [3] | Mousa A T. Inversion Algorithm for GPS down Looking Occultation Data: Simulation Analysis.Japan Earth and Planetary Science Joint Meeting, Tokyo, 2002:27-31. |
| [4] | Aoyama Y, Shoji Y, Mousa A, et al. Down Looking GPS Occultation Measurement on the Top of Mt Fuji. Proceeding of International Workshop on GPS Meteorology. Tsukuba, Japan, 2003. |
| [5] | 张训械, 曾桢, 胡雄, 等. 山基无线电掩星模拟. 电波科学学报, 2004, 19, (5): 530–536. |
| [6] | 胡雄, 张训械, 吴小成, 等. 山基GPS掩星观测实验及其反演原理. 地球物理学报, 2006, 49, (1): 22–27. |
| [7] | 宫晓艳, 胡雄, 吴小成, 等. 雾灵山GPS掩星观测试验分析. 应用气象学报, 2008, 19, (2): 180–187. DOI:10.11898/1001-7313.20080233 |
| [8] | 吴小成, 胡雄, 宫晓艳, 等. 山基GPS掩星折射率与探空折射率比较. 地球物理学进展, 2008, 23, (4): 1149–1155. |
| [9] | 范磊, 符养, 杜晓勇, 等. 雾灵山山基掩星观测反演误差分析. 武汉大学学报:信息科学版, 2008, 33, (1): 89–92. |
| [10] | 孙学金, 赵世军, 余鹏. GPS掩星切点水平漂移规律的数值研究. 应用气象学报, 2004, 15, (2): 174–180. |
| [11] | 杜明斌, 杨引明, 丁金才. COSMIC反演精度和有关特性的检验. 应用气象学报, 2009, 20, (5): 586–593. DOI:10.11898/1001-7313.20090510 |
| [12] | Jensen A S, Lohmann M S, Benzon H H, et al. Full spectrum inversion of radio occultation signals. Radio Sci, 2003, 38, (3). DOI:10.1029/2002RS002763 |
| [13] | 胡雄, 曾桢, 张训械, 等. 大气GPS掩星观测反演方法. 地球物理学报, 2005, 48, (4): 768–774. |
| [14] | 肖卫华, 符养, 高太长, 等. 利用折射指数推算大气纬圈平均风场方法. 应用气象学报, 2011, 22, (3): 346–355. DOI:10.11898/1001-7313.20110311 |
| [15] | Born M, Wolf E. Principle of Optics. New York: Cambridge Univ Press, 1999. |
| [16] | 王名才. 大气科学常用公式. 北京: 气象出版社, 1994. |
 2012, 23 (4): 493-499
2012, 23 (4): 493-499



