2. 中国气象局数值预报中心,北京 100081;
3. 国家气象中心,北京 100081
2. CMA Numerical Predication Center, Beijing 100081;
3. National Meteorological Center, Beijing 100081
集合预报技术在过去的二十多年里取得了巨大进步,现已成为数值天气预报的重要组成部分,并在水文预报等领域也得到了广泛应用。但是集合预报仍受模式误差及初值扰动技术的限制,使得预报结果离散度不足,预报分布存在偏差。为了提高集合预报系统的预报技巧,近几年,在传统的数值模式后处理技术如MOS (Model Output Statistics) 方法[1-2]的基础上,一系列基于各种统计方法的校准技术被广泛用于国外集合预报概率产品的校准。这些方法包括贝叶斯模式平均 (BMA)[3], 非齐次高斯回归 (NGR)[4], Logistic回归[5-6], Analog技术[7-8],类似Kalman滤波的自适应误差订正技术[9]等。国内也开展了针对集合预报后处理技术的研究及应用,林春泽等[10]基于TIGGE资料,利用超级集合平均、多模式集合平均和消除偏差集合平均3种方法对多模式集合预报的地面气温预报进行集成;马清等[11]采用自适应误差订正技术进行了B08RDP多中心区域集合预报系统2 m温度预报结果的偏差订正。这些技术各具特点,但校准效果仍受到相关条件的限制,使其具有一定的适用性,如BMA在校正多模式集合预报时才能体现其优势,训练数据的大小对Analog技术和Logistic回归技术的校准效果有明显的影响等。
本文研究对象是国家气象中心区域集合预报系统的2 m温度预报,已有相关研究[12]对2008年北京奥运会期间包括国家气象中心在内的B08RDP各参与成员的2 m温度预报进行了较全面的评估,发现大部分系统对2 m温度的预报都存在着偏差和离散度不够的问题。Alexander等[13]研究结果表明,NGR技术在训练期较短的情况下,仍能有效校准具有高斯分布特征的连续变量 (如2 m温度) 的集合平均偏差和集合离散度,且校准过程简单。因此,本文将采用NGR技术进行区域集合预报系统2 m温度预报的校准研究,并通过综合的集合预报检验评分来检验校准前后的预报效果,最后初步开展NGR技术与自适应误差订正技术的比较研究。
1 区域集合预报系统及资料简介国家气象中心区域集合预报系统是依托于B08-RDP项目而发展的[14],该系统共有15个集合成员,模式系统为中尺度模式WRF,模式水平分辨率为15 km×15 km,垂直层次为35层;初值扰动技术采用增长模繁殖法,侧边界来自于T213模式的全球集合预报系统;模式扰动技术采用的是多物理过程参数化方案方法。B08RDP期间,区域集合预报系统的预报范围是华北地区,此后对该系统进行了加入陆面过程NOAH方案及拓展预报区域到全国范围的升级试验,并于2010年7月实现了升级后的区域集合预报系统的准业务运行。
本文将以国家气象中心区域集合预报系统2008年7月20日—8月20日每日12:00(世界时,下同) 起报的2 m温度预报为研究资料,开展校准技术应用和分析试验。检验的观测资料采用预报区域 (30~45°N, 105~125°E) 内400个地面站每3 h的2 m温度观测资料。为了便于直接使用,先采用双线性插值法将格点预报结果插值到站点。
2 非齐次高斯回归校正技术原理及应用非齐次高斯回归 (NGR) 是Gneiting等[4]基于标准线性回归而发展的针对集合预报的后处理技术,与其他集合预报校准技术相比,其显著优点是在训练期较短的情况下,仍能有效校准具有高斯分布特征的连续变量。
2 m温度预报是区域集合预报系统的重要预报变量之一,其预报准确率被预报员所关注。研究表明:2 m温度的观测统计近似服从正态分布,因此从理论上讲,校准后的集合平均和方差可以用来表示2 m温度正态分布的位置和形状。在NGR方法中,集合平均和方差由线性回归技术获得,而回归过程中方差随着预报因子的值而发生变化,因此,这种回归又是非均匀的。
NGR技术所模拟的具有正态分布形式的2 m温度预报概率密度函数为
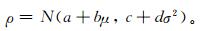
|
(1) |
式 (1) 中,μ是集合平均,σ是标准差 (集合离散度)。a, b, c, d是待定的回归系数,其中系数a和b表示偏差的特征,系数c和d表示集合预报离散度-技巧关系。本文采用最小连续分级概率评分 (简称CRPS) 来确定变量概率密度函数的参数。
CRPS是一种定量比较预报累计分布概率与观测累计分布概率距离差异的集合预报概率评分方法。对于一个连续型预报量x,其概率密度函数为ρ(x),观测值为xa,则连续分级概率评分计算公式可表示为
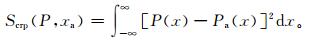
|
(2) |
P, Pa分别表示集合概率预报和观测值的累计分布函数:
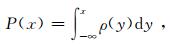
|
(3) |
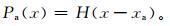
|
(4) |
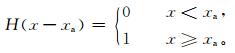
|
(5) |
当预报变量满足高斯分布时,一定训练期内的CRPS可以由式 (1) 中的系数a, b, c和d解析地表示出:
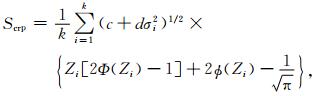
|
(6) |
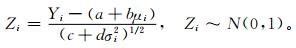
|
(7) |
这里,Φ是累积分布函数,ϕ是概率密度函数,k是训练期的长度 (单位:d),Yi是第i天的观测值。
采用Nelder等[15]提出的单纯形法来迭代估算回归系数,然后由回归系数可计算出式 (1) 中校准后的集合平均和离散度。为了便于比较校准前后每个成员的预报结果,必须利用正态分布函数计算出校准后的每个成员值。当集合成员为n时,一种可选方法是,由标准正态分布的第i/(n+1) 个分位函数计算第i个集合成员值[16],但是这种方法校准后的集合离散度偏大。为了克服这一缺陷,Alexander等[13]发展了依赖于预报概率的正态分布的分位函数技术,通过限定校准后的离散度范围,从而重新调整各集合成员的分位函数值,使得校准后的离散度更合理,然后根据校准后的集合平均和离散度来确定不同集合成员的预报。本文采用上述方法来计算校准后的集合成员的预报值:
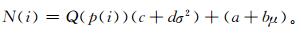
|
(8) |
这里,Q(p(i)) 是标准正态分布的分位函数,第i个成员的概率p(i) 为
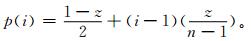
|
(9) |
z是调整后的集合预报的百分位面积。其值根据限制条件σ≤fE循环计算而得到。其中,σ为标准差,f为离散度因子,E为均方根误差。f由最小的CRPS结果确定,本文将在后面章节讨论f的敏感性。经过试验分析,当前采用f=1。
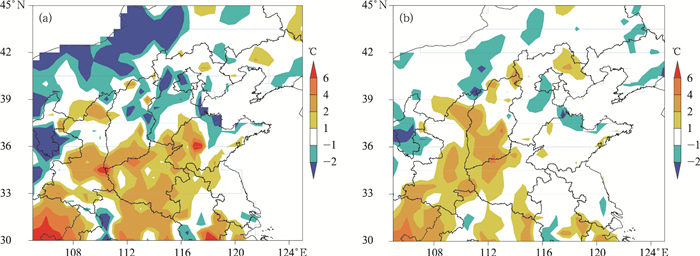
图 1是校准前后集合平均与观测场之差的地理分布图。整体上看,校准前预报区域西北部集合平均偏小,南部偏大,并且在四川东部,陕西、山西和河南三省交界处,山东中部,合肥南部有些区域预报存在异常偏大 (红色) 现象,校准后整个预报区域与观测值更接近,预报区域西北部、南部的预报得到明显改善,且原异常区域的预报值也均得到合理改善。
|
|
| 图 1. 2008年7月20日12:00起报的2 m温度集合平均 (预报时效为30 h) 与观测场之差的空间分布 (a) 校准前,(b) 校准后 Fig 1. Distribution of the difference of 30-hour 2 m temperation forecast at 1200 UTC 20 July 2008 (a) the difference between ensemble averge of model direct output and observation, (b) the difference between calibrated ensemble average and observation | |
3 校准结果 3.1 集合平均均方根误差和集合离散度的关系
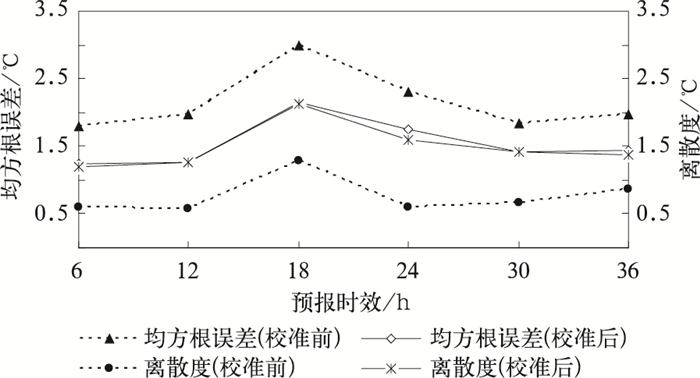
集合平均均方根误差和集合预报离散度的关系是衡量集合预报系统可靠性的一个重要标准,一个好的集合预报系统的集合平均均方根误差和集合离散度应该基本一致。图 2给出了校准前后2 m温度预报的集合平均均方根误差和集合离散度的预报时效演变图。从图 2可看出,校准前模式直接输出的预报存在明显的偏差并且离散度过小,而校准后的均方根误差明显减小,减小幅度为0.6℃左右, 同时校准后的集合离散度也明显增大,与集合平均均方根误差非常接近。
|
|
| 图 2. 2 m温度预报的均方根误差和离散度 Fig 2. RMSE and ensemble spread of 2 m temperature | |
3.2 Talagrand直方图分析
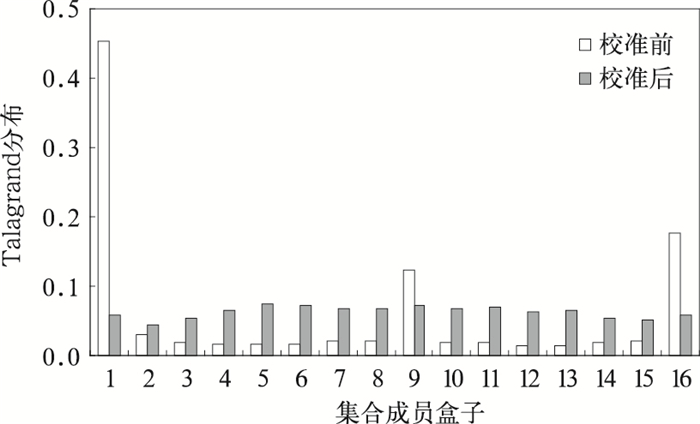
Talagrand直方图是衡量集合预报成员分布与观测值分布是否一致的评分,能够反映出集合预报系统可靠性及系统偏差的特征。对于具有完美离散度的集合预报系统,Talagrand表现出比较平坦的分布特征。图 3给出了校准前后6 h预报的2 m温度Talagrand直方图。由图 3可以看出,校准前的Talagrand分布表现出明显的“L”型分布,这说明集合系统的离散度偏小,并有暖偏差的特征,另外校准前Talagrand直方图中的第9个集合成员盒子表现出了比较显著的高频率,这可能和集合预报系统的系统偏差有关。校准后Talagrand的分布比较平缓,观测值基本以相同的概率落在各盒子中,预报系统的集合离散度得到显著改进,同时,原来出现在第9个盒子的明显偏差也得到了改进,说明集合成员分布更合理。
|
|
| 图 3. 2 m温度预报Talagrand分布 Fig 3. Talagrand diagrams of raw and calibrated 2 m temperature (forecast lead time is 6 hours) | |
3.3 Brier评分
Brier评分 (简称BS) 是计算预报概率误差的一种概率评分,计算公式可表示为
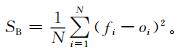
|
(9) |
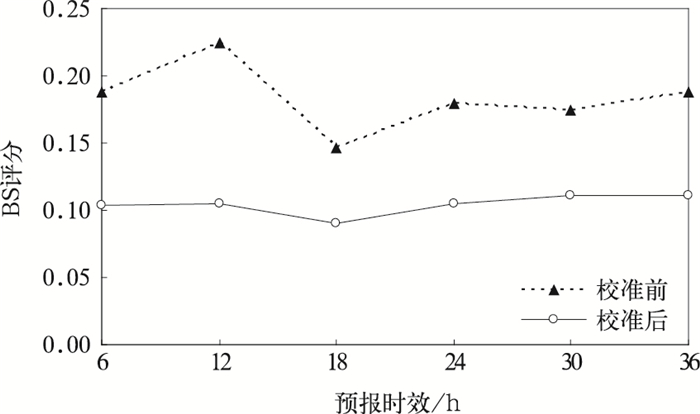
其中,N是被检验的二分类事件的样本数;fi是事件发生的预报概率;oi是事件观测概率,当事件发生时oi=1,不发生时oi=0。由此可知,SB取值范围是0~1,评分越小预报效果越好,SB= 0表示预报完全正确,SB= 1表示预报无效。本文以2 m温度距平大于1个标准差为二分类事件,计算出校准前后各预报时效的BS评分 (图 4)。相比于原模式直接输出,校准后温度的预报技巧有显著提高,其中12 h预报的BS评分提高最显著。整体上,校准后各时效预报的BS评分比较接近,表明校准后系统的预报能力更为稳定。
|
|
| 图 4. 2 m温度预报BS评分 Fig 4. BS of raw and calibrated 2 m temperature | |
3.4 CRPS评分
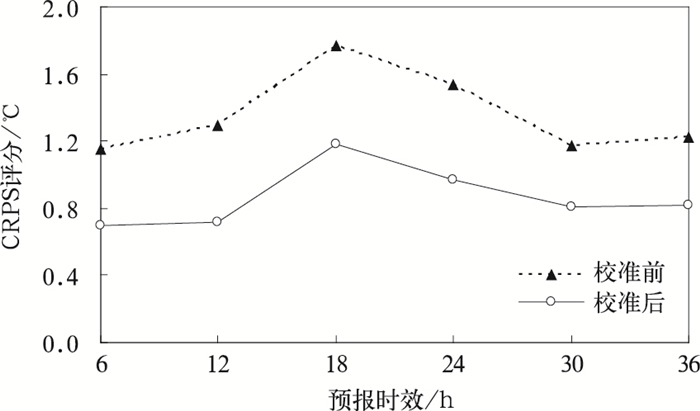
CRPS是评价集合预报系统整体性能的定量评分,其值越小表示预报的概率密度和观测的差值越小,预报系统预报能力越高。图 5给出了校准前后2 m温度预报的CRPS评分,可以发现经过NGR方法校准后的CRPS显著减小,减小幅度为0.4℃左右。
|
|
| 图 5. 2 m温度预报CRPS评分 Fig 5. CRPS of raw and calibrated 2 m temperature | |
3.5 ROC分析
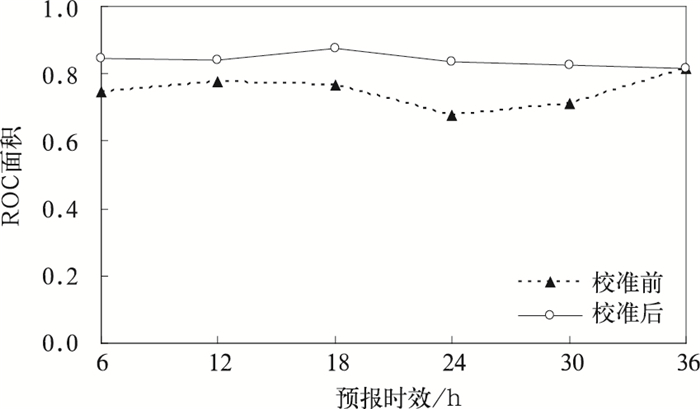
相对作用特征 (ROC) 是信号探测理论在数值天气预报中的一种应用[17]。用观测值检验预报发生或不发生两种状态,计算出的预报假警报率和命中率在平面直角坐标系中构成的曲线为ROC曲线。一个完美的预报假警报率为0,命中率为1,将命中率沿假警报率增加的方向积分就可得到ROC面积。ROC面积越大,预报技巧越高,若面积小于0.5,则预报无技巧。图 6中给出了二分类事件距平大于1个标准差在不同预报时次的ROC面积。由图 6可以看出,校准后各时效预报的ROC面积相对校正前均有了明显提高,说明NGR技术也能有效提高集合系统对事件的辨别能力,另外,校准后的ROC面积曲线更平缓,说明系统预报能力稳定。
|
|
| 图 6. 2 m温度预报ROC面积 Fig 6. Area under ROC curves for 2 m temperature | |
4 敏感性试验 4.1 不同训练期的校准结果对比
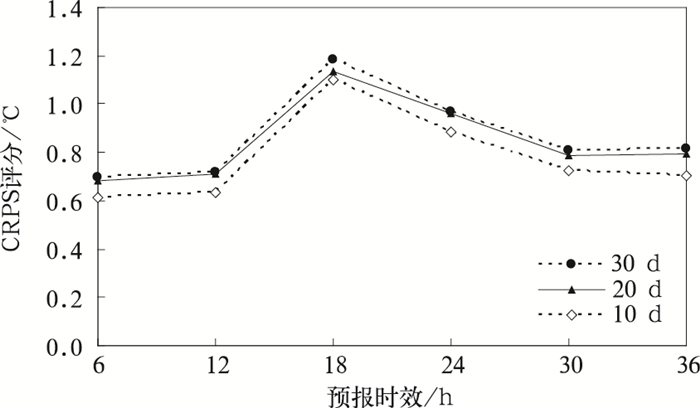
训练期的选取直接影响校准技术对集合预报系统的校准效果[5-7]。图 7给出了不同训练期的2m温度CRPS评分结果,从图 7中可看出20 d,30 d训练期的CRPS差别很小,10 d训练期的校正效果最好。因此,对于NGR技术而言,当训练期的时间序列较短时,NGR技术仍能有效校准2 m温度预报,甚至可能取得更好的校准效果,上述结果与前人的研究结果[13, 16]类似。
|
|
| 图 7. 不同训练期的2 m温度预报CRPS评分 Fig 7. CRPS of 2 m temperature from different training length | |
4.2 不同离散度因子f对校准结果的影响
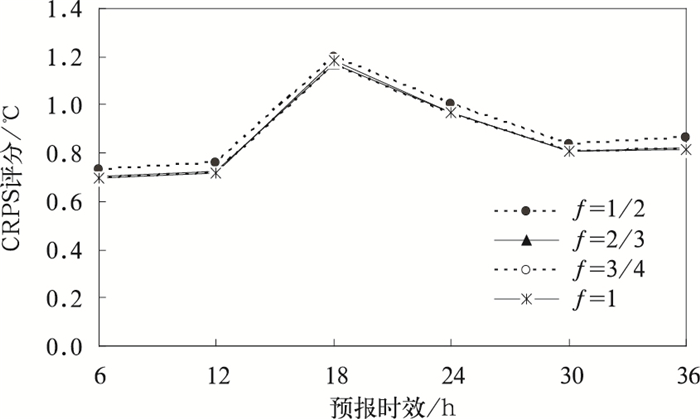
由第2章可知,离散度因子f决定了校准后的预报概率密度函数的形状,因此,本文开展了利用不同离散度因子校准预报的敏感试验。图 8是分别采用f等于1/2,2/3,3/4和1调整集合离散度后的预报结果的CRPS评分。对比发现,当f=1/2时, CRPS评分相对偏大,而其他取值CRPS评分相差很小,因此本文选取离散度因子f=1。
|
|
| 图 8. 不同离散度因子的2 m温度预报CRPS评分 Fig 8. CRPS of 2 m temperature from different spread rescaling | |
5 NGR技术与自适应误差订正技术的对比试验
上述结果证明了NGR技术能够显著校准区域集合预报系统2 m温度预报的系统偏差和提高集合离散度。在此,将通过NGR技术与自适应误差订正技术的对比试验,进一步说明该方法的可适用性。
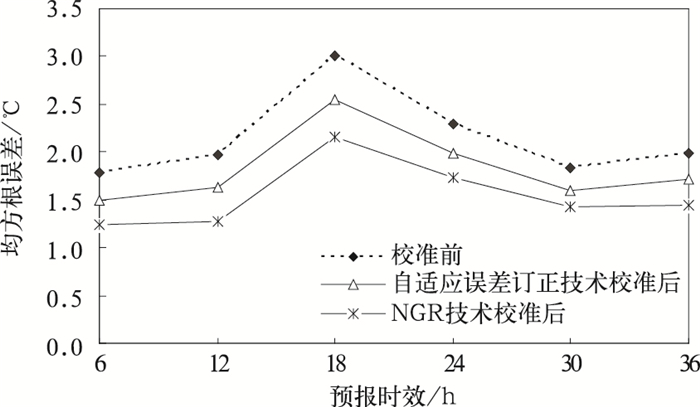
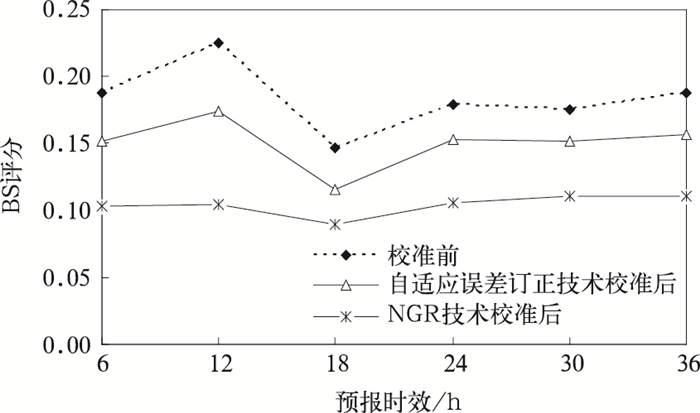
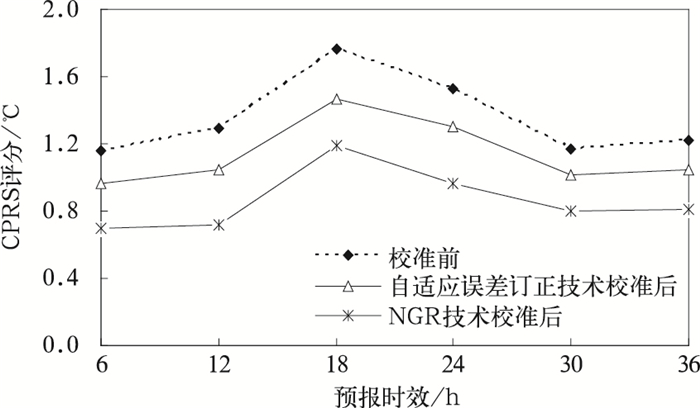
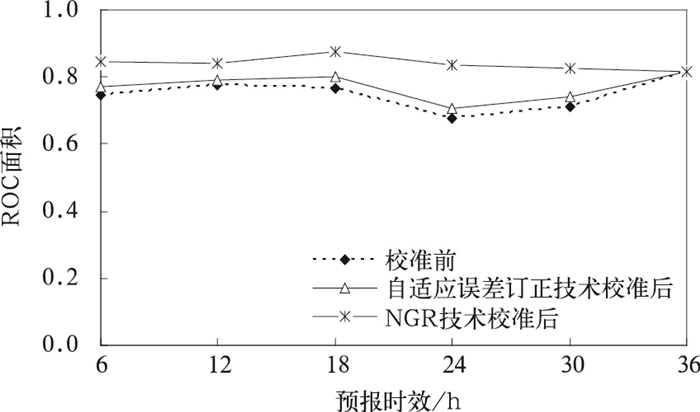
为了便于直接比较校准结果,自适应误差订正技术也将以相同的区域集合预报结果和观测资料为研究资料。校准过程中,对修正系数实行冷启动[8],相应地使用w=3.3%为权重系数。结果表明,自适应误差订正技术校准一阶矩系统误差效果明显,但对二阶离散度校准作用甚微 (图略),这与Cui等[9]的研究结果一致。因此下面主要对两种技术校准系统误差的效果进行比较。图 9给出了原模式直接输出及两种校准技术校准后的集合平均误差变化状况。由图 9可以看出,NGR技术和自适应误差订正技术分别在不同程度校准了2 m温度预报的系统误差,但NGR校正效果更好。从BS评分 (图 10)、CRPS评分 (图 11) 及ROC面积 (图 12) 各项检验指标可以看出,相对于自适应误差订正技术而言,NGR技术能更加显著地提高2 m温度预报技巧。
|
|
| 图 9. 2 m温度预报的均方根误差 Fig 9. RMSE of 2 m temperature | |
|
|
| 图 10. 2 m温度预报的BS评分 Fig 10. BS of 2 m temperature | |
|
|
| 图 11. 2 m温度预报的CRPS评分 Fig 11. CRPS of 2 m temperature | |
|
|
| 图 12. 2 m温度预报ROC面积 Fig 12. Area under ROC curves for 2 m temperature | |
6 小结
本文基于NGR技术开展了区域集合预报系统2 m温度预报的后处理校准技术研究,实现了对其一阶偏差和二阶离散度的校准,并初步开展了NGR技术与自适应误差订正技术的比较试验。通过对校准前后2 m温度预报较全面的检验分析,得到以下主要结论:
1) NGR技术对2 m温度预报的集合离散度和均方根误差校准效果显著,校准后的均方根误差减小,集合离散度增大,两者之间的离散度-预报技巧关系显著提高。Talagrand直方图的检验结果表明,NGR技术能有效改进2 m温度预报离散度不足的缺陷,并且显著减小了原Talagrand直方图中的暖偏差现象和第9个排序区间的明显偏差,使得校准后的集合成员分布更均匀。
2) 在相同的温度阈值下,BS评分、ROC面积和CRPS评分的检验结果均表明,经NGR技术校准后的2 m温度的预报能力显著提高,其中包括了对特定阈值的鉴别能力。
3) 不同训练期的校准结果对比试验表明,时间序列较短时,NGR技术对原模式预报校准效果仍然显著。而目前的校准技术大多都是训练期越长校准效果越明显,因此NGR技术校准效果受训练数据影响小的特点使其更具有普遍适用性。
4) NGR技术与自适应误差订正技术的对比试验表明,NGR技术对集合平均误差的校准效果更显著。同时,BS评分和CRPS评分等也表明,NGR技术要优于自适应误差订正技术。
| [1] | Carter G M, Dallavalle J P, Glahn H R. Statistical forecasts based on the National Meteorological Center's numerical weather prediction system. Wea Forecasting, 1989, 4: 401–412. DOI:10.1175/1520-0434(1989)004<0401:SFBOTN>2.0.CO;2 |
| [2] | Vislocky R L, Fritsch J M. Performance of an advanced MOS system in the 1996-97 national collegiate weather forecasting contest. Bull Amer Meteor Soc, 1997, 78: 2851–2857. DOI:10.1175/1520-0477(1997)078<2851:POAAMS>2.0.CO;2 |
| [3] | Raftery A E, Gneiting T, Balabdaoui F, et al. Using Bayesian model averaging to calibrate forecast ensembles. Mon Wea Rev, 2005, 133: 1155–1174. DOI:10.1175/MWR2906.1 |
| [4] | Gneiting T, Raftery A E, Westveld A H, et al. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon Wea Rev, 2005, 133: 1098–1118. DOI:10.1175/MWR2904.1 |
| [5] | Hamill T M, Whitaker J S, Wei X. Ensemble reforecasting: Improving medium range forecast skill using retro-spective forecasts. Mon Wea Rev, 2004, 132: 1434–1447. DOI:10.1175/1520-0493(2004)132<1434:ERIMFS>2.0.CO;2 |
| [6] | Hamill T M, Whitaker J S. Probabilistic quantitative precipitation forecasts based on reforecast analogs: Theory and application. Mon Wea Rev, 2006, 134: 3209–3229. DOI:10.1175/MWR3237.1 |
| [7] | Hamill T M, Whitaker J S. Ensemble calibration of 500-hPa geopotential height and 850-hPa and 2-m temperatures using reforecasts. Mon Wea Rev, 2007, 135: 3273–3280. DOI:10.1175/MWR3468.1 |
| [8] | Hamill T M, Whitaker J S, Mullen S L. Reforecasts: An important dataset for improving weather predictions. Bull Amer Meteor Soc, 2006, 87: 33–46. DOI:10.1175/BAMS-87-1-33 |
| [9] | Cui B, Toth Z, Zhu Y, et al. The Trade-off in Bias Correction Between Using the Latest Analysis/Modeling System with a Short, Versus an Older System with a Long Archive. Proc First THORPEX Int Science Symp, Montreal, Canada, World Meteorological Organization, 2006:281-284. |
| [10] | 林春泽, 智协飞, 韩艳, 等. 基于TIGGE资料的地面气温多模式超级集合预报研究. 应用气象学报, 2009, 20, (6): 706–712. DOI:10.11898/1001-7313.20090608 |
| [11] | 马清, 龚建东, 李莉, 等. 超级集合预报的误差订正与集成研究. 气象, 2008, 34, (3): 42–48. DOI:10.7519/j.issn.1000-0526.2008.03.007 |
| [12] | Kunii M, Saito K, Seko H, et al. Verifications and intercomparisons of mesoscale ensemble prediction systems in B08RDP. Tellus, 2011, 63A: 531–549. |
| [13] | Alexander Kann, Wittmann Christpoh, Wang Yong. Calibrating 2 m temperature of limmited-area ensember forecasts using high-resolution analysis. Mon Wea Rew, 2009, 137: 3373–3387. DOI:10.1175/2009MWR2793.1 |
| [14] | 邓国, 龚建东, 邓莲堂, 等. 国家级区域集合预报系统研发和性能检验. 应用气象学报, 2010, 21, (5): 513–523. DOI:10.11898/1001-7313.20100501 |
| [15] | Nelder J A, Mead R. A simplex method for function minimization. Comput J, 1965, 7: 308–313. DOI:10.1093/comjnl/7.4.308 |
| [16] | Hagedorn R, Hamill T M, Whitaker J S. Probabilistic forecast calibration using ECMWF and GFS ensemble reforecasts. Part Ⅰ: Temperature. Mon Wea Rev, 2008, 136: 2608–2619. DOI:10.1175/2007MWR2410.1 |
| [17] | 皇甫雪官. 国家气象中心集合数值预报检验评价. 应用气象学报, 2002, 13, (1): 29–36. |
 2012, 23 (4): 395-401
2012, 23 (4): 395-401



