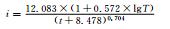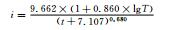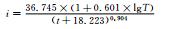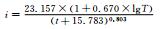设计暴雨是为防洪等工程设计拟定的、符合指定设计标准的、当地可能出现的暴雨，或定义为符合设计标准的暴雨量及其时程分配和面分布，同属于应用气象学和应用水文学两个学科。设计暴雨是区域防洪排涝和城市市政排水的重要基础，也是关系到区域安全和城市运行的重要问题。在全球变暖的大背景下，虽然不同地区有所差异，但极端强降水的频率和强度整体呈增大趋势^[1-4]，给区域防洪排涝和城市市政排水带来了更大的潜在压力。积极应对气候变化，特别是提高对极端天气气候变化的适应性，增强防灾减灾的能力，形势日益严峻和紧迫。因此，修订设计暴雨以适应新的气候状况势在必行。另外，以往可用的暴雨观测数据在时间和空间上都比较有限，导致设计暴雨不够精细：一是观测年限较短导致暴雨强度的推算不够精确，二是观测点不足导致地区差异在一定程度上被忽视。随着我国地面气象观测站网的建设和逐步完善，暴雨观测资料在时间和空间上不断丰富，以及设计暴雨强度推算方法研究的深入，都为细化和完善设计暴雨提供了良好的基础^[5-11]。

因设计需求不同，区域排涝和市政排水在设计暴雨方面的数据采样有明显差异。区域防洪排涝设计主要考虑历时24 h (72 h)、重现期在10年以上的暴雨强度，采用年最大值法采样；市政排水设计则主要考虑历时5~120 min、重现期在0.25~10年以内的暴雨强度，采用非年最大值法采样^[12]。1980年至今，我国地面气象观测站的基本整编资料包括每年15个历时的最大降水量，可作为防洪排涝设计的基础，但对市政排水设计则数据量不足 (无法估算重现期在1年以内的暴雨强度)。短历时极端强降水有很大的空间变率，因此尽可能最大限度地利用观测资料对于在空间上细化设计暴雨具有重要意义^[13-14]。

为此，本文选取天津市区和塘沽两个具有累年降水自记信息化数据的气象站，同时通过年最大值和年多样两种采样方法对暴雨强度进行推断，一方面对比分析两站暴雨强度的差异，另一方面分析基于年最大值采样的暴雨强度公式在市政排水设计方面的适用性和适用范围。

分别以天津市区气象站 (区站号54517，简称天津站) 和塘沽气象站 (区站号54623，简称塘沽站) 代表天津市区和滨海新区塘沽地区。所采用的数据包括：① 1980—2009年历年5，10，15，20，30，45，60，90，120，180，240，360，540，720 min和1440 min的最大降水量。数据抄录自地面气象观测记录年报表，每站30年共450个数值，其中天津站的数据完整率为87.5%，塘沽站为100%。② 1980—2009年历年上述15个历时的前10位最大降水量。数据统计自降水自记信息化数据和自动站分钟雨量数据，其中天津站2001—2004年空缺，塘沽站2001—2003年空缺，两站的数据完整率分别为86.7%和90%。数据不完整的原因是整编的降水自记信息化数据均截止于2000年，而自动站分钟雨量数据分别始于2005和2004年。

暴雨采样：年最大值和年多值两种方法。年最大值法即每年取最大值，国家气象站地面气象观测记录年报表中，历年15个历时最大降水量是年最大值采样数据。年多值法是将所有数据依降序排列，取前n个样本，使年平均样本量为3或4个。参照《室外排水设计规范GB50014-2006》^[15]有关原则，将各历时所有最大雨量 (每年前10位，总样本量是年限的10倍) 依降序排列，天津站 (样本年限26年) 取前104位，塘沽站 (样本年限27年) 取前108位，使得年平均样本量为4，从而可以推算最小重现期为0.25年的暴雨强度。

概率分布及其参数估计：极值Ⅰ型分布 (即耿贝尔分布) 和皮尔逊Ⅲ型分布 (即伽马分布)。耿贝尔分布用于拟合年最大值法采样的数据分布，伽马分布用于拟合年多值法采样的数据分布。概率密度函数的参数估计采用最大似然法。

概率分布拟合的统计显著性检验：卡方拟合适度检验 (简称卡方检验) 和科莫尔洛夫-斯米尔诺夫检验 (简称K-S检验)。检验的原假设H₀为样本的原始分布与拟合分布没有显著差异，备择假设H₁为样本的原始分布与拟合分布存在显著差异，显著性水平取0.05。

暴雨强度公式及其拟合：依《室外排水设计规范GB50014-2006》^[15]，暴雨强度总公式的形式为

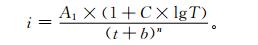
(1)

式 (1) 中，i为暴雨强度 (单位：mm·min^-1)；t为历时 (单位：min)；T为重现期 (单位：a)；A₁，b，C和n为待定参数，采用列文伯格-马夸尔特算法求解。

误差统计：均方根误差和相对均方根误差，或称绝对均方差和相对均方差^[16]。

对伽马分布拟合天津站和塘沽站5~120 min最大降水量 (年多值法采样) 的统计显著性检验表明，样本的原始分布与拟合分布没有显著差异。在误差统计方面，天津站5~120 min的平均绝对均方差为0.03 mm·min^-1，平均相对均方差为4.4%；塘沽站5~120 min的平均绝对均方差为0.04 mm·min^-1，平均相对均方差为4.7%。两站的误差均符合《室外排水设计规范GB50014-2006》^[15]的要求。

以耿贝尔分布对天津站和塘沽站各历时年最大降水量进行拟合，统计显著性检验认为样本的原始分布与拟合分布没有显著差异。天津站5~120 min历时的平均绝对均方差和相对均方差分别为0.09 mm·min^-1和7.0%，塘沽站分别为0.08 mm·min^-1和6.7%，与伽马分布的拟合相比，误差明显偏大。主要原因是对于年最大值采样而言，30个样本可能仍显偏少，特别是天津站还存在12.5%的数据空缺。

利用拟合的伽马分布推算天津站和塘沽站各历时降水量重现期为0.25，0.33，0.5，1，2，3，5，10，20，50年和100年的重现水平。图 1显示了天津站和塘沽站短历时降水量重现水平的对比。同时，利用拟合的耿贝尔分布推算天津站和塘沽站各历时暴雨强度为2，3，5，10，20，50年和100年的重现水平。表 1给出了塘沽站5~120 min历时、0.25~10年重现期暴雨强度相对于天津站的对比，以绝对均方差和相对均方差进行定量分析。由表 1可知，偏差非常明显，平均绝对均方差达0.1952 mm·min^-1，相对均方差达17.2%，而且各重现期的绝对均方差都超过了0.5 mm·min^-1，相对均方差都超过了5%。这表明，如果塘沽地区采用与天津市区同样的设计暴雨强度，不符合排水设计规范对误差的要求。虽然相距仅50 km左右，但塘沽位于滨海地区，短历时的暴雨强度要明显大于靠近内陆的天津市区。

图 1

图 1. 天津站和塘沽站短历时降水量重现水平的对比 Fig 1. Comparison of the short-time precipitation return level between Tianjin Station and Tanggu Station

表 1

表 1 塘沽站5~120 min暴雨强度相对于天津站偏差 Table 1 Deviation statistics of 5 to 120 minutes rainstorm intensity at Tanggu Station from that at Tianjing Station 重现期/a 绝对均方差/(mm·min-1) 相对均方差/% 0.25 0.2415 11.5 0.333 0.2564 15.3 0.5 0.2935 20.9 1 0.2555 20.9 2 0.2052 20.6 3 0.1277 16.3 5 0.1003 15.3 10 0.0815 16.6

表 1 塘沽站5~120 min暴雨强度相对于天津站偏差 Table 1 Deviation statistics of 5 to 120 minutes rainstorm intensity at Tanggu Station from that at Tianjing Station

统计耿贝尔分布推算值相对于伽马分布推算值的误差：市区站历时5~120 min，2~10年重现期暴雨强度的平均绝对均方差和相对均方差分别为0.1281 mm·min^-1和9.1%，塘沽站分别为0.1028 mm·min^-1和6.6%；天津站历时5~1440 min，2~100年重现期暴雨强度的平均绝对均方差和相对均方差分别为0.1897 mm·min^-1和16.6%，塘沽站分别为0.1144 mm·min^-1和9.2%。这两种分布推算值之间的误差，一方面与最初的暴雨数据采样方式有关，另一方面与伽马分布所拟合的数据中缺少2001—2004年的样本有关。天津站的误差较塘沽站明显偏大，主要与其年最大值的数据完整率不高有关。

以伽马分布推算的暴雨强度-历时-频率关系表涵盖5~1440 min共15个历时和0.25~100年共11个重现期 (按照市政排水设计需求，重点关注5~120 min，0.25~10年重现期的暴雨强度)。以耿贝尔分布推算的关系表则只包括2年及以上的重现期。分别以上述两种关系表拟合暴雨强度公式 (表 2)，误差统计表明所得公式基本符合《室外排水设计规范GB50014-2006》^[15]要求。两站对比表明，塘沽站的误差较大。需要指出的是，所得暴雨强度公式的计算范围 (历时、重现期) 不能超过其参数估计时所采用的样本的范围。

表 2

表 2 两类暴雨强度公式 Table 2 Two types of rainstorm intensity formula 站点 概率分布 历时t/min 重现期T/a 暴雨强度公式i/ (mm·min-1) 总绝对均方差/ (mm·min-1) 总相对均 方差/% 平均绝对 均方差/ (mm·min-1) 平均相对 均方差/% 天津站 伽马 5~120 0.25~10 0.0426 2.3 0.0386 4.3 耿贝尔 5~1440 2~100 0.0493 2.9 0.0458 3.8 塘沽站 伽马 5~120 0.25~10 0.0707 3.7 0.0623 6.2 耿贝尔 5~1440 2~100 0.0614 4.8 0.0587 4.8

表 2 两类暴雨强度公式 Table 2 Two types of rainstorm intensity formula

本文关注的问题是，一般气象站基于年最大值法采样的暴雨强度公式在市政排水设计方面的适用性。计算基于年最大值采样法的暴雨强度公式相对于伽马分布推算的暴雨强度的误差 (表 3) 可知，在2~10年重现期内，塘沽站的绝对均方差均小于0.05 mm·min^-1，相对均方差均小于5%。而天津站的误差稍大，这很可能与数据完整率不高有关。

表 3

表 3 基于年最大值采样法的暴雨强度公式相对于伽马分布推算的暴雨强度的误差统计 Table 3 Error statistics of the rainstorm intensity formula based on the annual-maximum data sampling against the estimated rainstorm intensity by Gamma distribution 重现期/a 天津站 塘沽站 绝对均方差/(mm·min-1) 相对均方差/% 绝对均方差/(mm·min-1) 相对均方差/% 2 0.0523 6.6 0.0438 4.8 3 0.0386 4.5 0.0303 3.0 5 0.0597 6.3 0.0251 2.3 10 0.0533 5.0 0.0457 3.6

表 3 基于年最大值采样法的暴雨强度公式相对于伽马分布推算的暴雨强度的误差统计 Table 3 Error statistics of the rainstorm intensity formula based on the annual-maximum data sampling against the estimated rainstorm intensity by Gamma distribution

对比基于两种数据采样法的暴雨强度公式的计算结果，同样以绝对均方差和相对均方差进行定量分析 (表 4)。结果表明：天津站和塘沽站的情形类似：当重现期为2~10年时，塘沽站两种公式的计算值很接近，绝对均方差基本都小于0.05 mm·min^-1，相对均方差也基本都小于5%；天津站两种公式计算重现期5~10年暴雨强度的误差较大，可能与其数据完整率不高有关。总的来说，当标准为2~10年一遇时，基于年最大值采样的暴雨强度公式在市政排水设计方面是适用的。

表 4

表 4 基于两种数据采样法的暴雨强度公式的计算值的对比 Table 4 Calculation comparison of two rainstorm intensity formulas with different methods of data sampling 重现期/a 天津站 塘沽站 绝对均方差/(mm·min-1) 相对均方差/% 绝对均方差/(mm·min-1) 相对均方差/% 2 0.0391 3.3 0.0470 3.4 3 0.0134 1.0 0.0428 2.9 5 0.0566 4.0 0.0404 2.4 10 0.1254 7.9 0.0433 2.3

表 4 基于两种数据采样法的暴雨强度公式的计算值的对比 Table 4 Calculation comparison of two rainstorm intensity formulas with different methods of data sampling

选取天津站和塘沽站两个具有长年分钟雨量资料的气象站，分别代表天津市区和滨海新区塘沽地区，基于年最大值和年多值两种数据采样方式对暴雨强度进行了推断，并分别编制了暴雨强度公式。对比分析两站暴雨强度的差异和两类暴雨强度公式的差异，结论如下：

1) 塘沽地区的暴雨强度较天津市区明显偏大，在市政排水设计上不宜采用与市区相同的标准。

2) 当标准为2~10年一遇时，基于年最大值采样法的暴雨强度公式的误差符合《室外排水设计规范GB50014-2006》^[15]的要求，因而在排水设计上具有适用性。