2. 中国气象科学研究院雷电物理和防护工程实验室,北京 100081
2. Laboratory of Lightning Physics and Protection, Chinese Academy of Meteorological Sciences, Beijing 100081
灾害损失评估和区划是灾害学的重要组成部分, 自然灾害本质上是极端的地球物理事件,灾害的发生由致灾环境的危险性和承灾体的脆弱性所决定。通常,致灾环境对一个区域来说,很大程度上是自然的、难以改变和无法完全控制的,而承灾体却不同,人为因素可以起到极为重要的作用。易损度作为人类社会对自然灾害敏感的程度, 它是人类社会组成和结构的函数, 该函数可以调整和改造[1], 影响和评价承灾体的易损性是防灾减灾的一种重要手段。国内外近几年的发展表明, 在科学研究基础上进行风险区划, 将自然灾害管理提高到风险管理水平,是所有可能避免和减轻自然灾害的措施中最简便有效的方法之一[2]。
雷电是大气中的放电现象,在过去的10年里通过卫星观测, 人们已经获取了大量闪电活动资料[3],这些闪电的发生正是雷电孕灾环境的直接反映。研究表明:绝大部分雷电灾害事故由雷暴中的地闪导致,雷击过程能够导致人员伤亡,引起油库和森林火灾, 造成供电及通讯信息系统故障或损坏, 对航天、航空、矿山及一些重要而敏感的高技术装备具有重大威胁[4]。雷电灾害造成人员伤亡更不容忽视,据统计[5],1964—1994年美国因雷击平均每年造成87人死亡,雷击死亡人数仅次于因山洪、洪水引发的死亡人数,雷电已经成为气象灾害中造成人员伤亡的重要因素,成为当今防灾减灾的重要对象。
近年来, 研究人员从雷灾易损性的角度出发, 以实证的方法对区域灾害进行了分析评估和区划。蒋勇军等[6]以灾害密度、灾害频数、经济损失模数、生命易损模数为评价指标,采用对称不等分间隔的五级分割法划分易损等级, 并赋予各等级定值,利用区域综合易损度对重庆自然灾害进行了评估和区划。严春银等[7]、郭虎等[8]、李彩莲等[9]用同样方法分别对江西、北京和陕西的雷电灾害进行易损度评估分析和区划,并给出了这些地区的雷电风险区划图;王惠等[10]在进行雷灾易损度的评估分级时,改用距平百分率计算各个评价指标,依据综合易损度指数给出了云南省雷电区划结果;戴建华等[11]利用TRMM/LIS资料分析了长三角地区的闪电活动规律。以上工作为雷电灾害的区域性防御提供了有益的帮助,本文从分析我国雷击致人伤亡的基本特征入手,采用R型聚类分析的方法筛选影响易损度的关键指标,应用这些关键指标采用Q型层次聚类分析法计算各种分类情况,对比聚合系数的陡度来确定分类数。为了验证聚类解的稳定和可信,采用两种方法进行对比,给出我国雷击致人伤亡的风险区划结果。
1 资料和方法 1.1 资料本文所使用的雷电灾害数据来源于全国雷电灾害数据库。该数据库包括我国自1997年以来各省、市、自治区上报的雷电灾害数据和事例 (其中未包含我国台湾省的相关资料)。由于资料收集的局限性,在部分年份、部分地区可能存在雷灾记录缺失或信息记载不规范的情况,因此本研究只是全国雷灾特征的不完全统计[12]。虽然我国开展雷电灾害收集和整理工作相对美国等国家时间较短,但该数据库是我国雷电灾害较为系统、完整和规范的可用资料。本文所用资料为1997—2010年全国分省雷击致人伤亡的数据。
地闪密度是雷电灾害中重要的致灾环境因子之一。虽然地闪密度可以依据各地的雷暴日数利用经验公式计算得到,但随着各地雷暴日数的不同,计算结果大不相同,特别是雷暴日数小于60 d时,不同经验公式计算结果会出现20%以上的偏差[13]。为了准确地反映孕灾环境的实际情况,本文采用卫星观测的闪电数据来计算各省区平均地闪密度。
20世纪90年代中期,美国国家航空航天局成功研制出新一代光学闪电成像仪OTD (optical transit detector) 和LIS (lightning imaging sensor), 并由低轨道卫星携带, 实现了相对有效、可靠的卫星闪电探测[14]。卫星闪电观测包含了云闪和地闪,大量观测结果表明,云闪与地闪的比例约为3:1,有些地区这个比例还要高[15], 虽然雷电灾害更多由地闪引发,但对于本文的研究没有实质性的影响。马明等[16]利用OTD观测的1995年4月—2000年3月全球80°S~80°N的闪电资料, 以及LIS观测的1997年12月—2005年12月全球37°S~37°N的闪电资料, 计算了我国各省区的平均地闪密度,该结果能够较准确地反映各区域雷电活动情况,文中所用数据来源于此计算结果。另外,我国各省、市、自治区的人口数、农村人口数和区域面积来源于2000年全国第5次人口普查资料。
1.2 方法表 1是1997—2010年我国各省 (市、自治区,其中未包含台湾省) 人口、面积、平均地闪密度、雷灾频数和雷击造成人员伤亡频数的统计情况。由表 1可以看出,变量数值相差较大且量纲不一致,当计算相似性测度时,数量级大的变量变差也往往较大,对相似性测度的贡献占主导地位,这样就可能掩盖了其他变差小的变量的影响。另外,当变量的测量单位变化时相似性测度的值也随之改变,有可能改变最终的分类结果,所以必须对表 1的数据进行标准化处理,将变量变换为方差为1、数学期望为0的标准化变量。
|
|
表 1 1997—2010年各省 (市、自治区) 雷灾情况统计 Table 1 The lightning disaster statistic for provinces in China from 1997 to 2010 |
为了克服以往雷电灾害区划方法的局限性,本研究将多元统计学中的聚类分析引入雷电灾害的区划中。在聚类分析中,对变量的分类筛选称为R型聚类,对样本的分类常称为Q型聚类,聚类分析中首先要计算所有样本的相似性测度,表征相似性测度最常用的是欧氏距离和Pearson相关系数。欧氏距离其实就是多维空间中的点距,两个点距离越小,表示两者关系越紧密,就越有可能分在同一类,相反,距离越大,表示两者间差异越大,分在同一类的可能性较小。对变量或样本可以计算得到欧氏距离矩阵,为聚类做准备。
有了距离矩阵就可以采用分层的办法进行聚类,其原理是对于n个观测样本先分别作为独自的一类,将离得最近的两个观测样本合并为一类,这样剩下n-1类,再计算这n-1类两两之间的距离,找到离得最近的两个类将其合并,便剩下n-2类,……,直到剩下2类,将它们合并为1类为止,通过聚类进度表和二叉树聚类图可表征聚类过程的每一步聚合情况,每一步计算出来的聚合系数作为确定分类数的主要依据。这个过程可用多种方法来完成,由于观测样本的差异,采用不同方法可能得到不同结果,本文采用SPSS软件中的组内类平均联结法 (Within-groups linkage,简称Within法) 进行分类,并用离差平方和法 (Ward’s method,简称Ward’s法) 进行了检验[17],验证Within法的聚类解稳定可信。
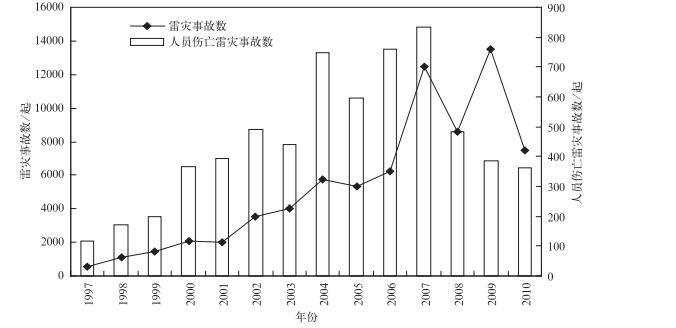
2 雷击致人伤亡的基本特征图 1给出了我国1997—2010年所发生的雷灾事故数与只造成人员伤亡的雷灾事故数的比较。14年间我国共发生雷电灾害74167起,平均每年发生5298起雷灾事故。雷击造成人员伤亡事故共计6355起,占雷灾事故总数的8.6%,平均每年发生454起。从图 1可以看出,我国雷电灾害事故呈现出逐年增加的总趋势,在2007年和2009年出现了双峰状态。人员伤亡事故数在2007年以前呈上升趋势,2007年以后则呈下降趋势。
|
|
| 图 1. 1997—2010年我国雷灾事故数与造成人员伤亡雷灾事故数比较 Fig 1. Comparison between accident number of lightning disasters and casualties in China from 1997 to 2010 | |
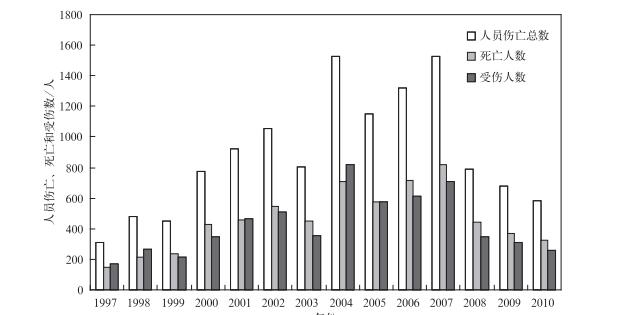
我国1997—2010年雷击死亡、受伤及伤亡人数的统计如图 2所示,14年雷击共造成12392人伤亡,平均每年885人。雷击致人伤亡呈现出双峰趋势,2004年和2007年出现最大值,伤亡人数分别为1527人和1528人,2004年以前逐年增加,而2007年以后逐年减少,死亡人数与受伤人数也较好地符合这个趋势。14年死亡人数为6446人,平均每年因雷击死亡460人,占伤亡数的52%,平均死伤比为1:0.92,高于美国死伤比1:2.54[5]。
|
|
| 图 2. 1997—2010年我国雷击人员伤亡、死亡和受伤人数变化 Fig 2. Annual number of lightning casualties, deaths and injuries in China from 1997 to 2010 | |
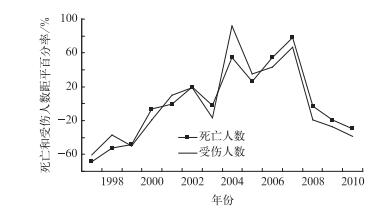
雷击死亡和受伤人数的距平百分率如图 3所示,每年平均死亡人数为460人,受伤人数为425人,死伤人数在2002,2004,2005,2006,2007年都出现了正距平,可见这些年份与常年相比死伤人数都偏高。死亡人数在2007年最高,比常年偏高78%;受伤人数在2004年最高,比常年偏高92%,距平百分率出现较大偏高可能与统计方法、雷暴日数和气温的变化有关[18]。
|
|
| 图 3. 1997—2010年我国雷击死伤人数距平百分率 Fig 3. Lightning deaths and injuries anomaly percent in China from 1997 to 2010 | |
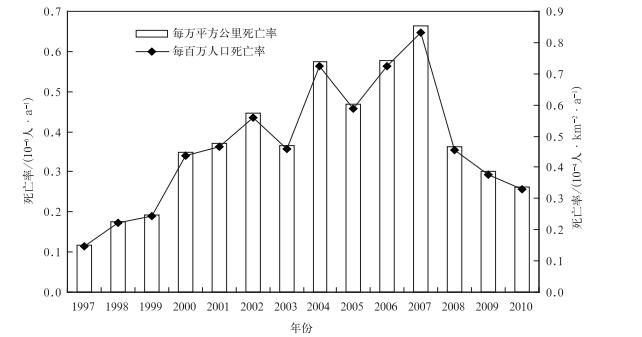
当考虑人口权重和人口密度因素时,可采用每年每百万人口死亡人数和每年每万平方公里死亡人数来统计。图 4给出了两个变量的变化特征,可见两个指标相关显著,在2007年以前呈现上升趋势,2007年到达最高值后呈下降趋势,这可能与近年来雷电预警预报提高、公众防雷意识的加强和医疗急救水平的提高有关[19]。
|
|
| 图 4. 1997—2010我国雷灾致人死亡率 Fig 4. The rate of lightning deaths in China from 1997 to 2010 | |
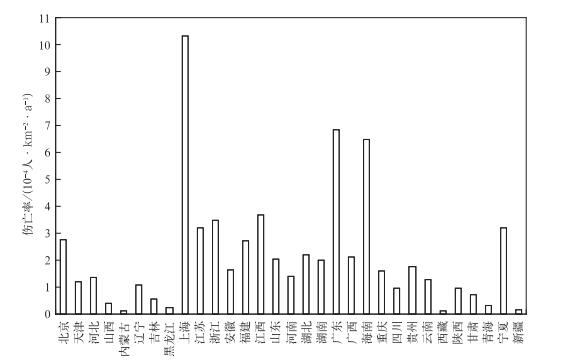
当不考虑每年人口基数的变化时,均选取2000年第5次人口普查数据计算,我国每年每百万人口平均雷击死亡率为0.36人,与美国的0.42人为同一数量级,约为新加坡1.7人的五分之一,与澳大利亚的0.001人相比大两个数量级[5],低于南非的6人和斯威士兰的15.5人[20]。图 5还给出了我国各省、市、自治区每年每万平方公里雷击致人伤亡人数,最高的上海市为10.32人,最低值出现在内蒙古和西藏,只有0.12人。14年全国平均值为0.48人,2007年达到峰值,为0.85人。
|
|
| 图 5. 1997—2010年我国雷灾致人伤亡率 Fig 5. The rate of lightning casualties in China from 1997 to 2010 | |
3 区域易损度评估与区划
雷电灾害致人伤亡随时间的变化特征,一定程度上反映了致灾因子产生的后果及不同时期的损害情况,然而要全面反映不同地区的损害程度,针对不同区域提出适实的防御措施,区域性易损度的评估与区划尤其重要。
3.1 区域易损度评估指标评估指标应反映孕灾环境和承灾体的特征,可以根据灾后损失评估体系采用反推法确定,也可基于社会易损性的理解、由灾害案例采用信息量法确定[6]。根据以上原则,选取雷击致人伤亡的8个影响因子,定义如下指标变量:① 平均地闪密度Ng,每平方公里每年发生的地闪次数,单位:次·km-2·a-1;② 雷灾频数F1,发生雷电灾害的年平均次数,单位:次·a-1;③ 人员伤亡频数F2,雷击造成人员伤亡的年平均人数,单位:人·a-1;④ 人口数N1,单位:万人;⑤ 农村人口数N2,单位:万人;⑥ 人口密度D1,单位:人·km-2;⑦ 农村人口密度D2,单位:人·km-2;⑧ 区域面积A,单位:104·km2。
由于各变量的量纲不一致,对以上8个变量的31个样本数据进行标准化处理,将变量变换为标准化变量。8个变量的提出来源于经验认知,将影响雷击致人伤亡易损度的因子都选出,但并不是每个因子都会在聚类分析中起作用,多元统计学指出[17],选择变量时要注意克服加入尽可能多的变量这种错误倾向,并不是加入的变量越多,得到的结果越客观,如果某些变量之间存在着较强的相关关系,不仅给问题的分析和描述带来一定困难,而且在使用某些统计方法时会出现多重共线性现象,很多变量无法在处理和分析中发挥作用,反而成了分析和解决问题的障碍。因此,利用R型聚类分析法对变量因子进行筛选,筛选过程如下:① 采用组内类平均联结法对8个变量进行R型模糊聚类。变量分为5类:Ng,(F1,F2),(N1,N2,D2),D1,A,每类挑选1个变量,取5个变量:Ng,F2,N1,D1,A。② 用离差平方和法进行验证。该方法也将变量分为5类:Ng,(F1,F2),(N1,N2),(D1,D2),A,每类挑选1个变量,也可取5个变量:Ng,F2,N1,D1,A,两种方法对变量的挑选结果一致,说明聚类解可信,聚类冰柱图 6较好地反映了上述验证结果。③ 去除中间变量。由于变量D1由N1与A计算而得 (D1=N1/A),因此去除变量D1,剩下4个变量:Ng,F2,N1,A。④ 皮尔逊相关系数检验,8个变量的皮尔逊相关系数计算结果见表 2,结果显示Ng,F2,N1,A这4个变量的相关系数均小于0.6。因此最后选取Ng,F2,N1,A这4个变量对样本进行Q型模糊聚类。
|
|
表 2 8个变量之间的皮尔逊相关系数检验表 Table 2 The Pearson correlations of variables |

|
|
| 图 6. Within法和Ward’s法冰柱图 Fig 6. Vertical icicle plots of Within and Ward's cluster | |
3.2 易损度区划与评估 3.2.1 易损度分类区划
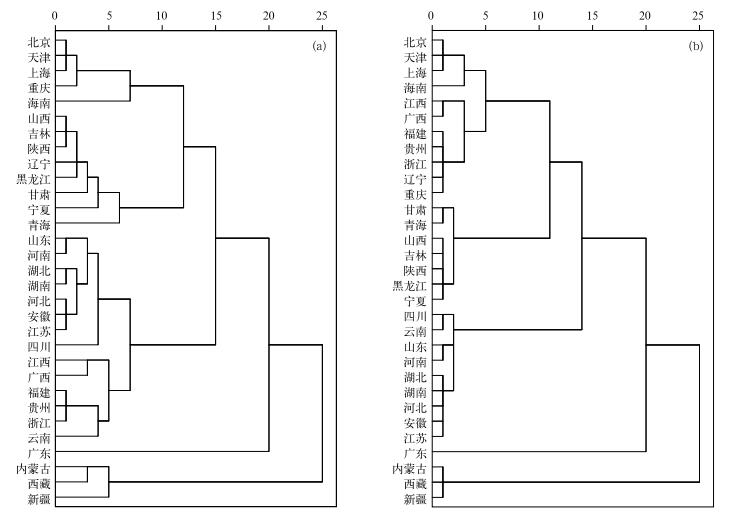
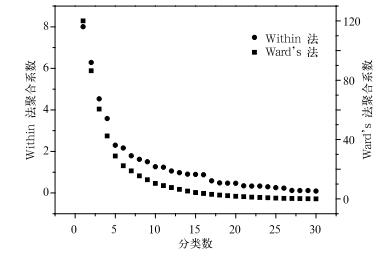
取平均地闪密度 (Ng)、人员伤亡频数 (F2)、人口数 (N1) 和区域面积 (A)4个指标变量的标准化值,对31个样本采用Within法进行Q型聚类分析,得到了图 7a的二叉树聚类图。从图 7a可以看出,将31个样本分成1~31类的所有情况,为了便于比较,图顶部x轴 (0~25) 是聚类过程中各类间的距离测度映射而得,树形图显示了分层聚类过程中,从每一个样本单独的一类,逐次合并,直到全部合并成一大类,整个过程都在图中充分体现,聚类过程进行了30步,每一步都计算出1个聚合系数。由图 8可以看出, 分类数在6类以内时各类之间的斜率较大,即数值差较大,说明各类的距离测度较远,分类理想,所以采用6级分类,前面计算聚类图时已经计算了从分成1~31类的所有分类值,从中取6类值得到下面结果:{北京,天津,上海,重庆,海南},{山西,吉林,陕西,辽宁,黑龙江,甘肃,宁夏,青海},{山东,河南,湖北,湖南,河北,安徽,江苏,四川},{江西,广西,福建,贵州,浙江,云南},{广东},{内蒙古,西藏,新疆}。
|
|
| 图 7. 二叉树聚类图 (图中x轴是SPSS计算的类间距离测度映射值) (a) Within法, (b) Ward’s法 Fig 7. Dendrogram of cluster (x axis is the mapping value of cluster distance with SPSS numeration) (a) Within method, (b) Ward's method | |
|
|
| 图 8. 不同分类数下聚合系数变化 Fig 8. The coefficients variety under the number of cluster | |
为了验证以上聚类解的稳定性,采用Ward’s法取相同的4个指标变量的标准化值,对31个样本进行Q型聚类分析,得到图 7b的二叉树聚类图,聚类过程也进行了30步,每一步都计算出1个聚合系数。由图 8可以看出,6类以内的聚合系数之间的陡度很大,表示分成6类后各类之间的距离测度相对较远,分类较果较好,证实了分类数为6类是可信解。由图 7b中取6类值得到如下结果:{北京,天津,上海,海南},{山西,吉林,陕西,黑龙江,甘肃,宁夏,青海},{山东,河南,湖北,湖南,河北,安徽,江苏,四川,云南},{江西,广西,福建,贵州,浙江,辽宁,重庆},{广东},{内蒙古,西藏,新疆}。对比Within法,辽宁、重庆和云南分类改变,其余均没有变化,聚类解稳定。
聚类分析方法中,由于原始数据的误差 (资料收集的局限性,雷灾记录缺失或信息记载不规范) 总会不同程度地存在着离散的奇异值,以Within法的结果分别计算6类的每年每万平方公里的人员伤亡数,可以看出在0.14~6.85之间,类最高值仅为6.85,然而从图 5的计算发现上海和海南,分别高达10.32和6.47,分别高出本类{北京, 天津, 上海, 重庆, 海南}平均值3.15的2倍和1倍左右,上海和海南在本类中明现出现不合理的奇异值,通常认为孕灾环境应具有连续性的特征,在相同地理环境和相同气候背景下孕灾环境基本是一致的,那么承灾体的易损性就是相似的,根据这一原则就可去除奇异值,将海南并入{广东}类,将上海并入{山东, 河南, 湖北, 湖南, 河北, 安徽, 江苏, 四川}类,将重庆和河北互换,最后得到如下6类分类结果{北京, 天津, 河北}, {山西, 吉林, 陕西, 辽宁, 黑龙江, 甘肃, 宁夏, 青海}, {山东, 河南, 湖北, 湖南, 重庆, 安徽, 江苏, 上海, 四川}, {江西, 广西, 福建, 贵州, 浙江, 云南}, {广东, 海南}, {内蒙古, 西藏, 新疆}。
3.2.2 易损度区划结果解释和证实对聚类结果进行解释是希望对各个类的特征进行准确的描述,给每类定义一个合适的易损度,这一步可以借助各类的特征量来进行分析,在前面的指标筛选中,最终确定了平均地闪密度、人员伤亡频数、人口数和区域面积4个指标为分类变量,根据这4个变量取平均地闪密度、每年每万平方公里的人员伤亡率和每年每百万人口的人员伤亡率来计算各类的特征值 (表 3)。
|
|
表 3 各区域所在类别的特征值 Table 3 The eigenvalue of cluster |
由表 3可以看出,区域平均地闪密度为2.22~16.32次·km-2·a-1,人员伤亡率分别为0.14×10-4~6.79×10-4人·km-2·a-1和0.35×10-6~1.52×10-6人·a-1,平均地闪密度最大的区域,人员伤亡率往往也最大,然而平均地闪密度较小的区域人员伤亡率也会出现较大的情况,为了准确描述各类易损度,先将这3个特征值进行标准化处理,再计算3个量纲为1的变量的综合易损值,按照综合易损值来分类,综合易损值越大的易损度越高,雷击致人伤亡的风险越大 (表 4)。
|
|
表 4 各类别的综合易损值 Table 4 The comprehensive vulnerability evaluation of cluster |
{广东,海南}综合易损值高达5.017为第1类地区,该区域雷击致人伤亡的易损度最高,属高风险区划区;第2类地区{江西,广西,福建,贵州,浙江,云南},属次高风险区; 第3类地区{山东,河南,湖北,湖南,重庆,安徽,江苏,上海,四川}和第4类地区{北京,天津,河北},均属中等风险区;第5类地区{内蒙古,西藏,新疆}和第6类地区{山西,吉林,陕西,辽宁,黑龙江,甘肃,宁夏,青海},均属弱风险区。
进一步分析各类的特征量发现,区域地闪密度按类别从高到低依次排列,第1类地区高达16.32次·km2·a-1,第6类地区只有2.22次·km2·a-1,第1类地区雷电灾害的孕灾环境最严重。将区域内每年每万平方公里人员伤亡率也按类别从高到低排列,发现第1类至第4类地区都是按从高到低依次排列,但第6类地区的0.57×10-4人·km-2·a-1比第5类地区的0.14×10-4人·km-2·a-1高,然而如果考虑每年每百万人口的人员伤亡率,第5类地区的1.22×10-6人·a-1又比第3类、第4类地区偏高,所以雷击致人伤亡风险的易损度大小不仅与区域孕灾环境有关,而有与区域人口密度相关。
4 结论和讨论本文利用1997—2010年全国雷电灾害数据库资料和卫星观测的闪电资料,分析了我国雷击致人伤亡的基本特征,并应用多元统计学中的聚类分析方法,对我国雷击致人伤亡进行了区域易损度的风险区划,得到以下结果:
1) 统计结果表明:我国雷击造成平均每年460人死亡,425人受伤,死伤比为1:0.92,每年每百万人口平均死亡人数为0.36人,每年每万平方公里平均死亡人数为0.48人。
2) 雷击造成人员伤亡的事故起数、每百万人口和每万平方公里死亡人数3个指标相关显著,在2007年以前呈上升趋势,2007年达到最高值后呈下降趋势,下降趋势可能与近年来雷电预警预报提高、公众防雷意识的加强和医疗急救水平的提高有关。死伤人数在2002,2004,2005,2006,2007年都出现了正距平,这些年份与常年相比死伤人数均偏高,死亡人数2007年最高,比常年偏高78%,距平百分率出现较大偏高可能与统计、雷暴日数和气温的变化有关。
3) 我国雷击致人伤亡的6类风险区划结果表明,广东和海南划为易损度极高的第1类地区,该类地区雷击致人伤亡的综合易损值高达5.017,无论是平均地闪密度还是人员伤亡率均为6类中最高,而划为第5类、第6类的我国西北和东北地区雷击致人伤亡的易损度较弱,属弱风险区域。对聚类结果的解释和验证发现,聚类解稳定可信,较好地反映了雷击致人伤亡这个随机事件的区域易损度特征。
易损度的评估和区划是自然灾害风险管理的重要手段,但是如何验证区划结果的可信度却是一个重要的问题,通常可以用同一种方法采用不同资料时段的计算结果来进行验证,也可以用同一资料采用不同方法计算结果来验证,前者最直接有效,美国从1900年开始每年收集发布了包含10个州雷灾引起人员伤亡的报告,1935年统计数据已经覆盖全国[18],长序列样本资料为区划结果的验证提供了帮助,而我国从1997年才开始组织上报雷电灾害资料,迄今仅有14年的资料,相比之下如果采用不同时段的资料进行验证,效果不会显著,因此本文选择了后者。当然随着我国雷灾资料上报年限的增加和上报制度的进一步规范,会应用更多的资料做出更为合理、更为客观的易损度区划结果,为切实有效地降低雷电带来的人员伤亡、保护人民生命安全服务。
| [1] | 郭跃. 灾害易损性研究的回顾与展望. 灾害学, 2005, 20, (4): 92–95. |
| [2] | 黄崇福, 张俊香, 陈志芬, 等. 自然灾害风险区划图的一个潜在发展方向. 自然灾害学报, 2004, 13, (2): 9–14. |
| [3] | Zhang Yijun, Ma Ming, Lu Weitao, et al. Review on climate characteristics of lightning activity. Acta Meteorologica Sinica, 2010, 24, (2): 137–138. |
| [4] | 张义军, 周秀骥. 雷电研究的回顾和进展. 应用气象学报, 2006, 17, (6): 829–833. |
| [5] | Curran E B, Holle R L, López R E. Lightning casualties and damages in the United States from 1959 to 1994. J Climate, 2000, 13: 3448–3463. DOI:10.1175/1520-0442(2000)013<3448:LCADIT>2.0.CO;2 |
| [6] | 蒋勇军, 况明生, 匡鸿海, 等. 区域易损性分析、评估及易损度区划. 灾害学, 2001, 16, (3): 59–64. |
| [7] | 严春银, 吴高学, 朱建章. 区域雷灾易损性及其区划的实证分析. 气象与环境学报, 2007, 23, (1): 17–21. |
| [8] | 郭虎, 熊亚军. 北京市雷电灾害易损性分析、评估及易损度区划. 应用气象学报, 2008, 19, (1): 35–39. |
| [9] | 李彩莲, 赵西社, 赵东, 等. 陕西省雷电灾害易损性分析、评估及易损度区划. 灾害学, 2008, 23, (4): 49–52. |
| [10] | 王惠, 邓勇, 尹丽云, 等. 云南省雷电灾害易损性分析及区划. 气象, 2007, 33, (12): 83–87. DOI:10.7519/j.issn.1000-0526.2007.12.012 |
| [11] | 戴建华, 秦虹, 郑杰. 用TRMM/LIS资料分析长江三角洲地区的闪电活动. 应用气象学报, 2005, 16, (6): 728–735. |
| [12] | 马明, 吕伟涛, 张义军, 等. 1997—2006年我国雷电灾情特征. 应用气象学报, 2008, 19, (4): 393–399. |
| [13] | 高燚, 劳小青, 李健生, 等. 雷击风险评估中雷击大地年平均密度的计算. 气象研究与应用, 2009, 30, (3): 68–69. |
| [14] | 张义军, 孟青, 马明, 等. 闪电探测技术发展和资料应用. 应用气象学报, 2006, 17, (5): 611–619. |
| [15] | Rakov V A, Uman M A. Lightning:Physics and Effects. Cambridge: Cambridge University Press, 2003: 44. |
| [16] | 马明, 吕伟涛, 张义军, 等. 我国雷电灾害及相关因素分析. 地球科学进展, 2008, 23, (8): 856–864. |
| [17] | 郭志刚. 社会统计分析方法. 北京: 中国人民大学出版社, 2005: 118–140. |
| [18] | López R E, Holle R L. Changes in the number of lightning deaths in the united states during the twentieth century. J Climate, 1998, 11: 2070–2076. DOI:10.1175/1520-0442-11.8.2070 |
| [19] | López R E, Holle R L. Fluctuations of lightning casualties in the United States:1959—1990. J Climate, 1996, 9: 608–614. DOI:10.1175/1520-0442(1996)009<0608:FOLCIT>2.0.CO;2 |
| [20] | Wisdom M D. Lightning fatalities in Swaziland: 2000—2007. Nat Hazards, 2009, 50: 179–191. DOI:10.1007/s11069-008-9331-6 |
 2012, 23 (3): 294-303
2012, 23 (3): 294-303



