2. 中国气象局公共气象服务中心,北京 100081
2. Public Meteorological Service Center, CMA, Beijing 100081
随着社会经济的快速发展,由自然态洪水造成的损失越来越大,防洪减灾任务迫切而艰巨。洪水预报是防洪非工程措施的关键技术之一。在洪水预报中,当洪水预见期大于流域集水时间和河道洪水传播时间,即降水转化至出口断面径流的时间小于洪水预见期时,基于观测降水的传统水文预报方法无法满足洪水预报与防洪减灾的要求。利用预见期内预报的定量降水进行洪水预报,是提高洪水预报精度与延长洪水预报预见期最有效的途径之一。
随着数值预报理论与方法的进一步发展以及计算机、大气遥感等科学技术的飞速进步,数值预报产品精度不断提高[1-3],定量降水预报 (Quantitative Precipitation Forecasts,QPF) 已经能够满足水文预报应用的要求[4-9],利用区域数值模式的定量降水预报产品驱动水文模型,不仅能够为水文模型提供所需要的相关空间描述,而且能够提供未来时刻降水演变信息。利用数值天气预报模式预报的定量降水预报产品作为洪水预见期内降水输入来延长洪水预报预见期、实现洪水预报已经成为可能。近年来,气象-水文耦合的洪水预报模式成为国内外研究的热点:谢正辉等[10-11]改进了VIC (Variable Infiltration Capacity) 模型中土壤蓄水曲线和土壤深度参数,构建了适用于区域气候模式的50 km分辨率的大尺度水文模型框架;雍斌等[12]、徐精文[13]基于蓄水容量曲线和TOPMODEL (TOPography based hydrological MODEL) 构建的XXT模型 (Xin'anjiang X TOPMODEL),并与NOAH-LSM (Land Surface Model) 模式耦合,获得良好的应用效果。陆桂华等[14]利用加拿大区域性中尺度模式MC2(Mesocale Compressible Community Model) 模拟的降水驱动集总式新安江模型,进行产汇流计算。Evans[15]在美国中部的FIFE试验期间,比较了4个区域气候模式分别耦合同一个水文模型得到的径流模拟结果。Anderson等[16]将Eta和HEC-HMS (the army corps of engineers' Hydrologic Engineering Center Hydrologic Modeling System) 单向耦合,用于预报水库入库流量,并提供48 h预见期的入库流量预报,为水库管理提供了决策支持。Collischonna等[17]在巴西Uruguay河Machadinho坝以上流域进行陆气耦合模式模拟,为水库的入流预报提供至少48 h预见期的入流预报,经过长时间模拟研究表明:耦合后的模式预报结果好于不考虑预见期内降雨的预报。Koussis等[18]和Amengual等[19]均用试验证明将气象模式与水文模型相耦合,能够延长洪水预报的预见期。
本文尝试将我国自主研发的全球-区域一体化数值预报系统[20-22](Global-Regional Assimilation and PrEdiction System,GRAPES) 和流域水文模型相耦合,建立GRAPES气象-水文模式,以研究GRAPES模式的定量降水预报产品对洪水预报的预见期延长效果。选择15 km×15 km和5 km×5 km两套模式水平分辨率,15 km×15 km分辨率的GRAPES模式由NCEP全球预报场提供初始场和侧边界条件;5 km×5 km分辨率的GRAPES模式由15 km×15 km分辨率GRAPES模式提供初始场和侧边界条件,将GRAPES_Meso模式的定量降水预报场分辨率统一降尺度到5 km×5 km分辨率,以满足分布式水文模型的输入要求。流域水文模型选取已在我国湿润、半湿润流域经过长期检验并有良好预报效果的新安江模型以及分布式新安江模型,与GRAPES模式单向耦合,构建GRAPES气象-水文模式,以淮河王家坝以上流域2009年汛期洪水为个例,进行模拟预报试验。
1 GRAPES_Meso模式简介GRAPES模式是由中国气象局于2000年开始组织研究开发的数值预报系统[22-24],GRAPES_Meso模式是其区域中尺度数值预报系统版,GRAPES采用全可压准静力平衡动力框架,半隐式半拉格朗日差分格式,水平Arakawa-C类跳点网格以及垂直Charney-Phillips跳层分布,并包含辐射、对流、微物理、垂直湍流扩散、陆面边界层等完整物理过程参数化方案,采用3D_VAR (3-Dimensional VARiational) 三维变分资料同化技术, 更进一步的详细介绍参阅文献[1-3]。GRAPES_Meso模式已先后在国家气象中心、广州区域气象中心、中国气象局上海台风研究所实现业务运行,表现出了较好的预报技巧[3, 25]。
2 流域水文模型简介 2.1 新安江模型简介新安江模型是一个分散参数的概念性水文模型,已经在我国洪水预报中得到了广泛应用。对于较大流域,根据流域下垫面的水文、地理信息将其分为若干个单元面积,将每个单元面积预报流量过程演算到流域出口,然后叠加起来即为整个流域的预报流量过程。三水源新安江模型由4个模块组成,分别为蒸散发计算、产流计算、分水源计算和汇流计算[26]。
2.2 分布式新安江模型简介分布式水文模型是水文模型的发展方向,基于栅格的分布式水文模型能够更加精确地描绘流域内下垫面的特性。本文选取分布式新安江模型。模型考虑栅格之间的水量交换以及河道排水网络的影响,将逐个栅格作为一个计算单元,进行3层蒸散发计算、蓄满产流计算及分水源计算,然后根据栅格演算次序矩阵,按照Muskingum-Cunge演算法逐栅格演算至流域的出口,地下径流则采用新安江模型中线性水库的方法演算至流域出口。
分布式新安江模型中,参数分为产流及分水源参数和汇流参数,通过研究发现,有些参数可以直接通过每个栅格单元的土壤类型和植被覆盖类型估计,如叶面指数[27]、最大叶面指数[27]、土壤田间持水量[28]、土壤凋萎含水量[28];有些参数可以通过其物理意义,与土壤类型及植被覆盖之间建立关系,如土壤的张力水蓄水容量[29-30]、表层土自由水容量[31]、深层蒸散发系数[32]、壤中流的出流系数[33]、地下水的出流系数[33]。逐栅格演算的Muskingum-Cunge演算法,其参数参照文献[34]的方法进行求解。剩余的参数,包括蒸散发折算系数,本文假定它们的取值在空间分布均匀,采用流域内统一赋值的方法。
本文采用美国马里兰大学 (UMD) 提供的全球30″×30″(近似于1 km×1 km) 分辨率的植被覆盖数据[35]描述研究流域内植被的空间分布,利用联合国粮农组织 (FAO) 提供的全球5′×5′(10 km×10 km) 分辨率的土壤类型数据[36]描述研究流域内土壤的空间分布。鉴于植被与土壤类型数据的精度,同时也为了提高模型的运行效率,在模型应用时所用的数字模型过程采用美国地质勘探局 (United States Geological Survey, USGS) 提供的分辨率为30″×30″的高程数据。
3 流域概况 3.1 淮河王家坝以上流域简化王家坝站以上流域为淮河上游,集水面积为30672 km2。本文将王家坝以上流域分为10部分, 采用基于子流域的新安江模型进行洪水预报。其中五沟营、板桥、薄山、宿鸭湖、南湾以及泼河6个子流域为淮河上游的大中型水库控制面积。子流域内雨量站见表 1,根据流域内水文站的布设和自然流域的边界,将水库出流作为下游子流域洪水预报的入流,对于每个子流域,根据其下垫面和水文特性以及雨量站分布,将其根据泰森多边形法划分为若干块,进行产汇流计算,逐子流域演算至流域出口断面。
|
|
表 1 王家坝站以上子流域单元雨量站 Table 1 Rain stations in the upper Wangjiaba Basin |
3.2 息县流域数字化
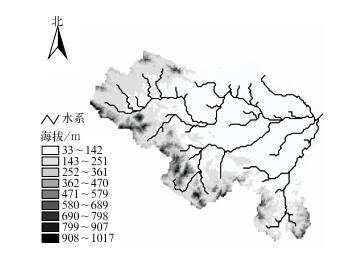
息县流域居淮河上游,流域面积8826 km2(不含大型水库面积)。本文采用分布式新安江模型对息县流域进行洪水预报,因而首先对息县流域进行数字化处理。根据TOPZ与ARCGIS技术,基于30″× 30″(近似于1 km×1 km) 分辨率的DEM数据进行数字水系提取,得到息县流域数字水系 (图 1)。由于流域单位元栅格DEM高程值是栅格内高程的平均值,因而对于流域河道栅格,其栅格DEM高程值必然远小于临近的流域坡面栅格DEM高程值。在基于DEM提取水系时,结合给定流域特征阈值,作为流域河道处理。在进行流域汇流计算时,使用坡面栅格汇流与河道栅格汇流两种方式进行计算。坡面栅格概化为宽浅虚拟河道进行汇流计算;河道栅格 (特别是河道宽度小于1 km的栅格) 由于高分辨率地形资料,概化为抛物线型河道断面进行汇流计算。
|
|
| 图 1. 息县流域数字水系图 Fig 1. Digital drainage map of Xixian Basin | |
4 数值试验
本文采用逐级降尺度模式的办法,以减缓较低分辨率气象模式与较高分辨率水文模型之间的耦合尺度不匹配的问题,即分辨率为1°×1°的美国NCEP全球预报场作为初始场和侧边界条件,驱动15 km×15 km的GRAPES_Meso模式 (GRAPES-15 km,覆盖区域为9.5°~54.5°N, 84°~144°E),以后者的预报场作为初始场和侧边界条件,驱动5 km×5 km的GRAPES_Meso模式 (GRAPES-5 km,覆盖区域为24.5°~39.5°N, 104°~124°E) 采用GRAPES_Meso模式与新安江模型、分布式新安江模型进行单向耦合,构建GRAPES气象-水文模式,以搭建试验模拟平台。
选择洪水灾害频发的淮河流域为试验流域,以GRAPES_Meso模式的定量降水预报场驱动新安江模型和分布式新安江模型,水文模型的输出时间间隔与GRAPES_Meso模式时间分辨率相同,为6 h,预报时长为60 h,从2009年8月28日08:00(北京时,下同)—9月9日14:00进行连续12 d的滚动预报。GRAPES气象-水文模式选取NCEP、观测降水和实测流量资料,每天08:00开始积分,时长为60 h,输出间隔为6 h,气象模式水平分辨率15 km×15 km或5 km×5 km,垂直分辨率为31层。以水文预报规范中的洪水预报的预见期、确定性系数、洪峰误差、洪量误差、峰现时间误差等水文要素来检验,评估GRAPES气象-水文模式的洪水预报精度,以及模式对洪水预报的预见期的延长效果。由于分布式新安江模型水平分辨率为30″× 30″,与GRAPES模式进行单行耦合时,水文模型的降水输入栅格被包含于GRAPES模式的定量降水预报栅格中,因而水文模型的降水输入直接读取对应的GRAPES模式的栅格预报降水。即假设气象模式栅格 (以下简称气象栅格) 内 (5 km×5 km) 的面雨量与该栅格内所包含的水文栅格 (1 km×1 km) 面雨量总和相等,且该气象栅格内的水文栅格获取的雨量处处相等,于是有
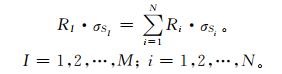
|
(1) |
式 (1) 中,σSI=5 km×5 km, 为气象栅格面积,RI为气象栅格的降水量;σSi=1 km×1 km, 为水文栅格面积;Ri为水文栅格的降水量;M为气象栅格数;N为水文栅格数,一般情况下M≤N。由于假设气象栅格内的水文栅格获取的雨量处处相等,即R1=R2=…=Ri=…=RN,于是式 (1) 变为
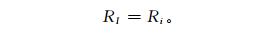
|
(2) |
模式程序中根据以上假设进行计算。
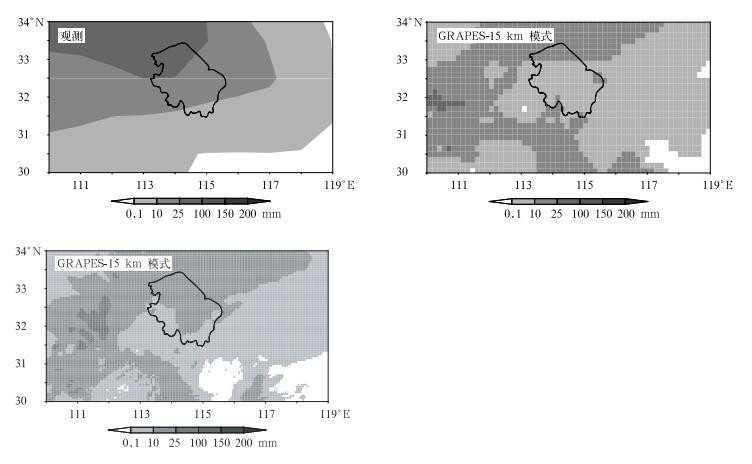
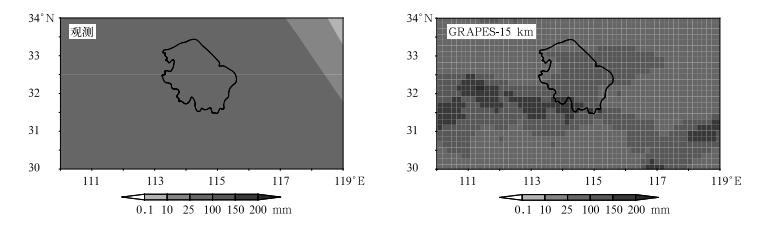
5 预报结果 5.1 GRAPES模式预报降水产品图 2给出了2009年8月29日08:00—14:00的6 h累积降水量分布,其中观测降水量、GRAPES-15 km及GRAPES-5 km模式预报降水起始时间为2009年8月28日14:00。GRAPES-15 km模式和GRAPES-5 km模式的18~24 h预报降水分布非常接近,与实况较为一致;模式预报的强降水中心位置比实际情况略偏北或者偏东;由图 3可以看出:GRAPES模式进行连续12 d的滚动预报,预报累积降水分布与实况降水相比整体一致。
|
|
| 图 2. 2009年8月29日08:00—14:00累积降水量 (曲线所包围区域为试验区域,下同) Fig 2. Accumulated precipitation from 0800 BT to 1400 BT on 29 Aug 2009 (the circled area is Wangjiaba Basin for test) | |
|
|
| 图 3. 2009年8月28日08:00—8月30日20:00累积降水量 Fig 3. Accumulated precipitation from 0800 BT 28 Aug 2009 to 2000 BT 30 Aug 2009 | |
5.2 GRAPES模式与新安江模型耦合的预报应用结果
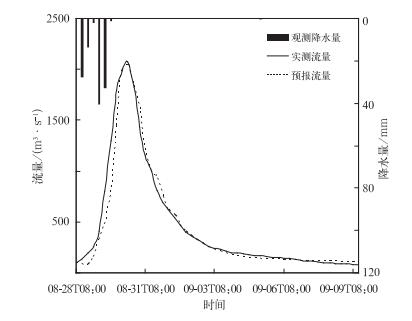
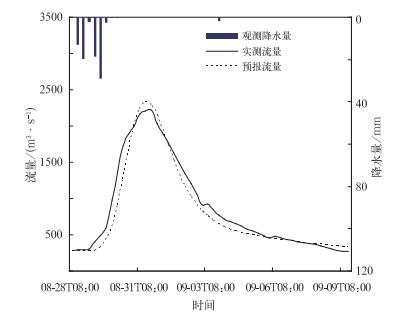
本次选取王家坝站以上流域的2009年汛期的一次长时间洪水过程,进行模拟试验,洪水时间为2009年8月28日08:00—9月9日14:00,流域内主要降雨从8月28日14:00开始至8月30日08:00结束,在8月31日20:00达到洪峰,峰值为2220 m3·s-1。本次试验选择的试验流域位于淮河上游,属于湿润流域,反映为典型的蓄满产流机制,因而选择在我国防汛和水利部门广泛应用的新安江模型。模拟结果如图 4所示,从整体来看模拟流量过程与实测流量过程相比,其洪峰相对误差为-4.9%,洪量相对误差为7.51%,确定性系数为0.95,模拟的洪水过程线与实测过程线非常吻合。
|
|
| 图 4. 2009年8月28日—9月9日王家坝站以上流域流量与水文模型模拟流量时间演变 Fig 4. The observed hydrographs against predictions in Wangjiaba Basin from 28 Aug to 9 Sep in 2009 | |
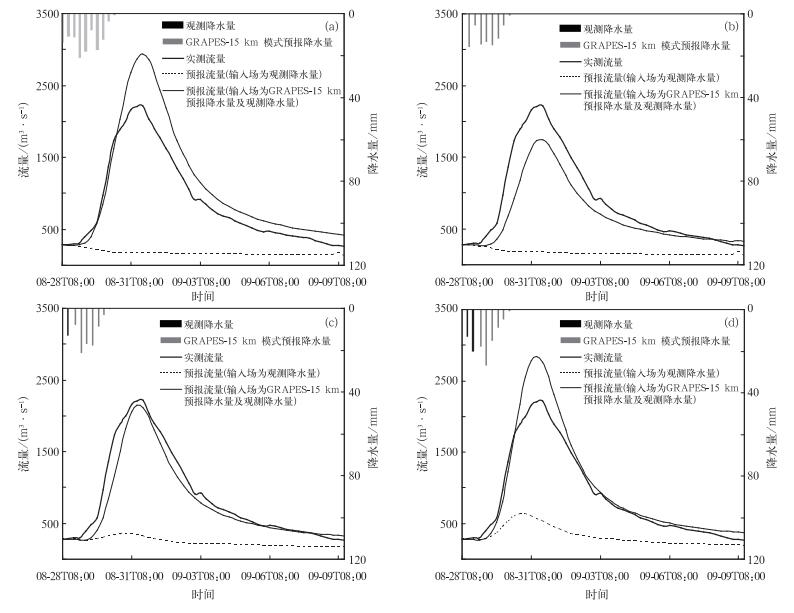
利用GRAPES-15 km模式和GRAPES-5 km模式预报降水驱动新安江模型进行连续12 d的滚动预报的流量过程线 (图 5,表 2)。在预见期84 h至66 h,GRAPES气象-水文模式模拟的流量过程与观测流量过程线拟合较好,其中GRAPES-15 km模式的确定性系数可达到0.93,GRAPES-5 km确定性系数可达到0.95,而基于观测降水模拟的流量过程线确定性系数仅达到-0.39(表 2);洪水的洪峰出现在8月31日20:00,基于观测降水模拟的流量在8月29日14:00才模拟出洪峰,预见期为30 h,而GRAPES气象-水文模式8月28日08:00就捕捉到了洪峰,预见期为84 h。这表明利用GRAPES模式的预报降水驱动水文模型可以延长洪水预报预见期;图 5a中以GRAPES-15 km模式预报降水驱动水文模型得到模拟流量偏大,原因在于模式对预见期内预报的累积降水量比观测的累积降水量偏大 (图 3),图 5d中GRAPES-15 km模式预报降水量比观测降水量稍大,且该试验流域在前12 h内已经达到蓄满,所以模拟出流量偏大,同时证明了GRAPES模拟预报降水量存在不确定性。在预见期84 h到54 h内,GRAPES气象-水文模式模拟洪水过程明显好于利用观测降水量模拟的洪水过程 (表 2),其中GRAPES-15 km模式预报降水模拟的洪峰相对误差、洪量相对误差和确定性系数来看要略好于GRAPES-5 km模式模拟结果,在峰现时间误差两种不同分辨率的模式模拟结果大致相当。
|
|
表 2 王家坝站以上流域新安江模型模拟结果统计 Table 2 Statistics of the application for Xin'anjiang Model in the upper Wangjiaba Basin |
|
|
| 图 5. 2009年8月28日—9月9日王家坝站以上流域流量与水文模型模拟流量时间演变 (a) 起始时间为2009年8月28日08:00, 预见期为84 h, (b) 起始时间为2009年8月28日14:00, 预见期为78 h, (c) 起始时间为2009年8月28日20:00, 预见期为72 h, (d) 起始时间为2009年8月29日02:00, 预见期为66 h Fig 5. Observed hydrographs and simulated hydrographs by hydrology model in Wangjiaba Basin from 28 Aug to 9 Sep in 2009 (a) initial time: 0800 BT 28 Aug 2009, lead-time: 84 h, (b) initial time: 1400 BT 28 Aug 2009, lead-time: 78 h, (c) initial time: 2000 BT 28 Aug 2009, lead-time: 72 h, (d) initial time: 0200 BT 29 Aug 2009, lead-time: 66 h | |
5.3 GRAPES模式与分布式水文模型相耦合应用结果
王家坝站以上流域为山区性流域,该流域下游为平原流域,由于资料的限制,本次选取息县流域为试验流域,选取蓄满产流机制的分布式新安江模型,模拟2009年汛期洪水。试验流域内的主要降水量从8月28日14:00持续到8月30日02:00,在8月30日14:00达到最大洪峰为2070 m3·s-1。以观测降水量作为分布式新安江模型的输入,在息县流域得到较好的模拟结果 (图 6),从整体来看模拟流量过程与实测流量过程相比,洪峰相对误差为-5.19%,洪量相对误差为-0.98%,确定性系数为0.96,模拟的洪水过程线与实测过程线非常吻合。
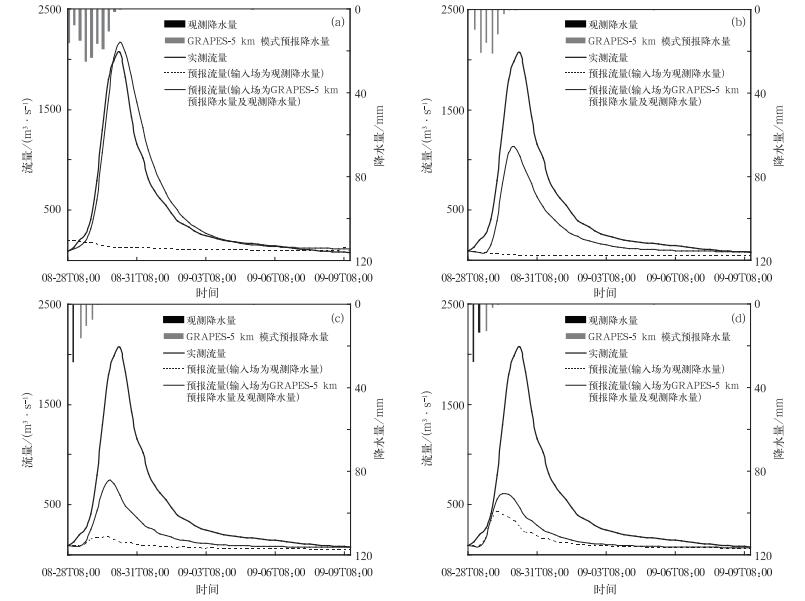
图 7给出了预见期为54 h至36 h的GRAPES-5 km预报降水驱动分布式新安江模型的模拟流量过程与实况的比较 (图 7,表 3)。GRAPES气象-水文模式在预见期54 h已经能较好地捕捉到洪峰;由于从预见期48 h到36 h,GRAPES模式预报降水量比观测降水量偏小,所以模拟的洪水过程也偏小 (图 7b~图 7d),流域内8月28日20:00才观测到明显的降水 (图 7c),但分布式新安江模型是蓄满产流机制的水文模型,因此模型将20:00出现的降水作为输入场进行流量模拟,未能模拟出洪峰。从表 3可以看出,随着洪水预报预见期的缩短,分布式新安江模型利用观测降水量模拟的流量过程洪水预报的洪量相对误差、洪峰相对误差、确定性系数和峰现时间误差上都在逐步减小。利用GRAPES-5 km模式预报降水驱动分布式新安江模型模拟的洪水过程线,在预见期为18 h和12 h两个阶段的模拟效果不理想,这主要是由于GRAPES模式在这两个时段对息县流域内降雨落区预报不准确。但总体来看,GRAPES-5 km模式的预报降水模拟结果优于GRAPES-15 km的预报降水模拟结果,这也与水文模型自身对输入场分辨率的要求有关,利用GRAPES-5 km模式的预报降水作为分布式新安江模型的输入数据,耦合匹配得更好。
|
|
表 3 息县站以上流域分布式新安江模型模拟结果 Table 3 Statistics of the application for distributed Xin'anjiang Model in Xixian Basin |
|
|
| 图 7. 同图 5,但为GRAPES-5 km模式预报6 h累加降水量 (a) 起始时间为2009年8月28日08:00, 预见期为54 h, (b) 起始时间为2009年8月28日14:00, 预见期为48 h, (c) 起始时间为2009年8月28日20:00,预见期为42 h, (d) 起始时间为2009年8月29日02:00,预见期为36 h Fig 7. Same as in Fig. 5, but for 6 h accumulated precipitation by GRAPES-5 km (a) initial time: 0800 BT 28 Aug 2009, lead-time: 54 h, (b) initial time: 1400 BT 28 Aug 2009, lead-time: 48 h, (c) initial time: 2000 BT 28 Aug 2009, lead-time: 42 h, (d) initial time: 0200 BT 29 Aug 2009, lead-time: 36 h | |
6 小结
本文研究结果表明:
1) 不同水平分辨率GRAPES-5 km模式预报降水与GRAPES-15 km模式的预报降水趋势一致,且5 km×5 km分辨率的预报降水量比15 km×15 km分辨率的预报降水量稍大。
2) 以GRAPES模式预报降水驱动水文模型较好地模拟了2009年汛期的一次洪水过程,且有效延长了洪水预报预见期。本文选用两个模型本身对输入分辨率的要求不同,所以选择与水文模型分辨率相匹配的降水预报场能够更好地对流域内水文过程进行模拟。
3) 由于GRAPES模式对某些时段降雨落区的预报还不十分准确,致使水文模型进行水文模拟时出现模拟流量偏大或是偏小,在分布式新安江模型结果中反映尤为明显,这也证明GRAPES模式预报精度还有待提高。
已有研究表明,数值模式考虑陆面模式反馈后,对降水预报有所改进。因此,GRAPES模式需考虑能模拟完整水循环的气象-水文双向反馈,使其与水文模型共享土壤含水量等下垫面影响因子的变化,这样既能够延长洪水预报的预见期并提高预报精度,还能够对降水预报的精度有所改善。
| [1] | 陈德辉, 薛纪善. 数值天气预报模式现状与展望. 气象学报, 2004, 62, (5): 623–633. DOI:10.11676/qxxb2004.061 |
| [2] | 矫梅燕. 现代数值预报业务. 北京: 气象出版社, 2010: 1–7. |
| [3] | 薛纪善, 陈德辉. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 2008: 334–335. |
| [4] | Hollingsworth A. Improvements in the Skill of Numerical Weather Prediction with Global Models. WMO Bulletin, 2003, 52: 33–39. |
| [5] | Collier C G, Krzysztofowicz R. Quantitative precipitation forecasting. J Hydrol, 2000, 239: 1–2. DOI:10.1016/S0022-1694(00)00389-9 |
| [6] | Damrath U, Doms G, Fruhwald D, et al. Operational quantitative precipitation forecasting at the German Weather Service. J Hydrol, 2000, 239: 260–285. DOI:10.1016/S0022-1694(00)00353-X |
| [7] | Golding B W. Quantitative precipitation forecasting in the UK. J Hydrol, 2000, 239: 286–305. DOI:10.1016/S0022-1694(00)00354-1 |
| [8] | McBride J L, Ebert E E. Verification of quantitative precipitation forecasts from operational numerical weather prediction models over Australia. Wea Forecasting, 2000, 15: 103–121. DOI:10.1175/1520-0434(2000)015<0103:VOQPFF>2.0.CO;2 |
| [9] | Mullen S L, Buizza R. Quantitative precipitation forecasts over the United States by the ECMWF Ensemble Prediction System. Mon Wea Rev, 2001, 129: 638–663. DOI:10.1175/1520-0493(2001)129<0638:QPFOTU>2.0.CO;2 |
| [10] | 谢正辉, 刘谦, 袁飞. 基于全国50 km×50 km网格的大尺度陆面水文模型框架. 水利学报, 2004, 5: 76–82. DOI:10.3321/j.issn:0559-9350.2004.03.013 |
| [11] | 谢正辉, 梁旭, 曾庆存. 陆面过程模式中地下水位的参数化及初步应用. 大气科学, 2004, 28, (3): 374–384. |
| [12] | 雍斌, 张万昌, 刘传胜. 水文模型与陆面模式耦合研究进展. 冰川冻土, 2006, 28, (6): 961–970. |
| [13] | 徐精文. 基于蓄水容量曲线和TOPMODEL概念的流域水文模型构建及其与NOAH LSM的耦合研究. 北京: 中国科学院, 2009. |
| [14] | 陆桂华. 陆气耦合技术应用研究进展. 2004年全国水文学术讨论会论文集, 2004: 14–20. |
| [15] | Evans J. Improving the characteristics of streamflow modeled by regional climate models. J Hydrol, 2003, 284: 211–227. DOI:10.1016/j.jhydrol.2003.08.003 |
| [16] | Anderson M L, Chen Z Q, Kavvas M L, et al. Coupling HEC-HMS with atmospheric models for prediction of watershed runoff. J Hydrol Eng, 2002, 7, (4): 312–318. DOI:10.1061/(ASCE)1084-0699(2002)7:4(312) |
| [17] | Collischonna W, Haasb R, Andreolli I, et al. Forecasting River Uruguay flow using rainfall forecasts from a regional weather-prediction model. J Hydrol, 2005, 305: 87–98. DOI:10.1016/j.jhydrol.2004.08.028 |
| [18] | Koussis A D, Lagouvardos K, Mazi K, et al. Flood forecasts for Urban Basin with integrated Hydro-Meteorlogical Model. J Hydrol Eng, 2003, 8, (1): 1–11. DOI:10.1061/(ASCE)1084-0699(2003)8:1(1) |
| [19] | Amengual A, Romero R, Gomez M, et al. A hydrometeorological modeling study of a f1ash-flood event over Catalonia, Spain. Journal of Hydrometeorology, 2007, 8: 282–303. DOI:10.1175/JHM577.1 |
| [20] | 陈德辉, 杨学胜, 江林, 等. 多尺度通用动力模式框架的设计策略. 应用气象学报, 2003, 14, (4): 452–461. |
| [21] | 陈德辉, 薛纪善, 杨学胜, 等. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究. 科学通报, 2008, 53, (20): 2396–2407. DOI:10.3321/j.issn:0023-074X.2008.20.002 |
| [22] | 陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17, (6): 773–777. |
| [23] | 伍湘君, 金之雁, 黄丽萍, 等. GRAPES模式软件框架与实现. 应用气象学报, 2005, 16, (4): 539–546. |
| [24] | 黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现. 应用气象学报, 2005, 16, (3): 374–383. |
| [25] | 王雨, 李莉. GRAPES_Meso V3.0模式预报效果检验. 应用气象学报, 2010, 21, (5): 524–533. |
| [26] | 赵人俊. 新安江模型的根据及参数与自然条件的关系. 北京: 水利电力出版社, 1994: 106–118. |
| [27] | Land Data Assimilation Schemes (LDAS), Mapped Vegetation Parameters. [2010-03-04]. http://ldas.gsfc.nasa.gov/LDAS8th/MAPPED.VEG/LDASmapveg.shtml. |
| [28] | Anderson R M, Koren V, Reed S. Using SSURGO data to improve Sacramento Model a priori parameter estimates. J Hydrol, 2006, 320: 103–106. DOI:10.1016/j.jhydrol.2005.07.020 |
| [29] | Koren V, Reed S, Smith M, et al. Hydrology laboratory research modeling system (HL-RMS) of the national weather service. J Hydrol, 2004, 291: 297–318. DOI:10.1016/j.jhydrol.2003.12.039 |
| [30] | 袁飞.考虑植被影响的水文过程模拟研究.南京:河海大学, 2006 |
| [31] | 姚成.基于栅格的新安江 (Grid-Xinanjiang) 模型研究.南京:河海大学, 2009. |
| [32] | 赵人俊, 王佩兰. 新安江模型参数的分析. 水文, 1988, 6: 2–9. |
| [33] | 赵人俊, 王佩兰, 胡凤彬, 等. 新安江模型的根据及模型参数与自然条件的关系. 河海大学学报, 1992, 20, (1): 52–59. |
| [34] | 包红军. 基于EPS的水文与水力学相结合的洪水预报模型研究. 南京: 河海大学, 2009. |
| [35] | University of Maryland, Department of Geography. UMD Land Cover Classification. [2010-03-04]. http://glcf.umiacs.umd.edu/data/landcover/. |
| [36] | Food and Agriculture Organization, Texture. [2010-03-04].http://www.ngdc.noaa.gov/ecosys/cdroms/reynolds/reynolds/reynolds.htm#tr. |
 2012, 23 (3): 274-284
2012, 23 (3): 274-284