应用气象学报  2012, 23 (2): 205-213   PDF    
引用本文
任玉玉, 任国玉, 周江兴. 我国大陆大尺度气候观测网的理想密度和分布[J]. 应用气象学报, 2012, 23(2): 205-213.
Ren Yuyu, Ren Guoyu, Zhou Jiangxing. The Ideal Density and Distribution of China Climate Network for Monitoring Surface Climate Change[J]. Journal of Applied Meteorological Science, 2012, 23(2): 205-213  
我国大陆大尺度气候观测网的理想密度和分布
任玉玉, 任国玉, 周江兴     
国家气候中心，北京 100081
2011-06-24 收到, 2011-12-15 收到修改稿.
资助项目: 公益性行业 (气象) 科研专项 (GYHY200906041)    
通讯作者: 任玉玉, E-mail: renyuyu@126.com.
摘要: 以我国大陆2416个气象观测站点组成的站网为参考，以观测序列的相关性表示对气候变化信号的监测能力，分析不同地区单位经纬度网格内站点数对信号监测能力的影响，得到特定监测能力要求下所需的站点数，为大尺度气候观测站网的站点设置提供科学依据。对2.5°×2.5°网格来说，当要求子集站网气温序列与标准站网气温序列相关系数超过0.99和0.95时，所需的站点数分别为750和377；当要求子集站网降水量序列与标准站网降水量序列的相关系数超过0.95和0.90时，需要的站点数分别为670和417。对2.5°×3.5°和5.0°×5.0°经纬度网格的分析发现，对站点数量要求较高的区域大部分是地形过渡区，一般来说，降水量观测对站点密度的要求高于气温。
关键词: 气候观测网    监测能力    气候变化    站网密度    
The Ideal Density and Distribution of China Climate Network for Monitoring Surface Climate Change
Ren Yuyu, Ren Guoyu, Zhou Jiangxing     
National Climate Center, Beijing 100081
Abstract: The China national climate observation network composed of 2416 stations are taken as the reference station network, and correlations of surface air temperature series precipitation series between the reference station network and analyzed station network are used to investigate the monitoring ability for surface climate change. The relationships between the monitoring requirements and the station number are analyzed for 2.5°by 2.5°, 2.5°by 3.5°, 5.0°by 5.0° latitude/longitude grid cells. Results show that the needed amount of stations decreases rapidly with the lowing of ability (standard) required for monitoring. Taking 2.5° by 2.5° grid cell for example, the needed amount of stations decreases from 750 to 377 when the monitoring requirements for temperature change from 0.99 to 0.95, and the needed amount of stations decreases from 670 to 417 when the monitoring requirements for precipitation change from 0.95 and 0.90. With the increase of grid cells, fewer stations are needed for the same monitoring requirement. In areas of rugged terrain, undulating terrain and transition zone from mountains to the plains and plateaus, higher station densities are generally needed. The areas where need high-density stations are mainly located in the mountainous regions, including the Sichuan Basin, the Wuyi Mountains, the Loess Plateau, the Qinling Mountains, the Southeast Hills, and the eastern mountainous areas of Northeast China. The more complex the terrain is, the lower the spatial consistency of climate change is, and the more stations are required. In general, monitoring for precipitation change requires higher density of stations. For 5° by 5° grid, however, the difference of station densities needed between temperature and precipitation is relatively small. The cause needs further study. The distributions of stations at the central and the west parts of Tibetan Plateau and Taklimakan Desert are not enough due to the harsh natural environment. Further research is needed in these regions, favorably in combination with other methods. In addition, the current stations are often located in the valleys and foothills rather than those on the slopes or on the peaks in mountainous regions, which has lowered the representativeness and enlarged the uncertainties.
Key words: climate observation network     monitoring ability     climate change     station density    
引言

为了监测、分析和预估气候变化，需要有理想的、可以稳定记录所在区域气候的观测站网[1-3]。已有的气象观测网为大气科学和气象业务发展奠定了基础，但由于当时条件所限，站址选择和网络规划时在一定程度上忽略了现代气候变化研究工作的要求，而我国目前对气象观测资料的研究侧重在数据的质量控制和均一性订正[4-10]，对台站的代表性问题重视不够。

Hubbard[11]的研究发现，在地势相对平缓、下垫面性质单一的地区，每60 km设置1个站点即可代表 90%的日气温的空间变化情况，而日降水则需要较高的观测密度 (5 km)。DeGaetano[12]对美国历史气候资料集814个站点季降水观测记录的分析发现，最少321个站点的资料就可以代表整个美国季降水量空间分布情况。Janis等[13-14]在设计最新的美国气候基准站网 (Climate Reference Network，CRN) 时，发现设置250个站点即可满足气候变化监测需要，相当于每隔180 km需要设置1个站点。赵瑞霞等[15]研究发现，同一地区，不同观测要素对站网密度的要求也会有较大差异。

受地貌等下垫面因素的影响，不同地区的站点所能代表的空间范围不同。在海拔高度变化较大的地区，站点所能代表的范围一般远小于地势平坦地区。因此，不同地区所需要的观测站点密度应有所不同。我国幅员辽阔，地形复杂，气候类型多样，各地对气候和气候变化观测站点密度的要求必然不同。本文假定在对同一地区的观测中，站网密度越大越能反映区域气候变化特征。在此基础上，借鉴von Storch等[16]和Janis等[13-14]确定站网密度的方法，分析确定我国在一定误差范围内可以代表区域主要气候要素 (气温，降水量) 的最优站点密度及其分布情况，探讨气候变化检测误差与站点数之间的关系，以期对国家大尺度气候观测网规划设计提供参考依据。

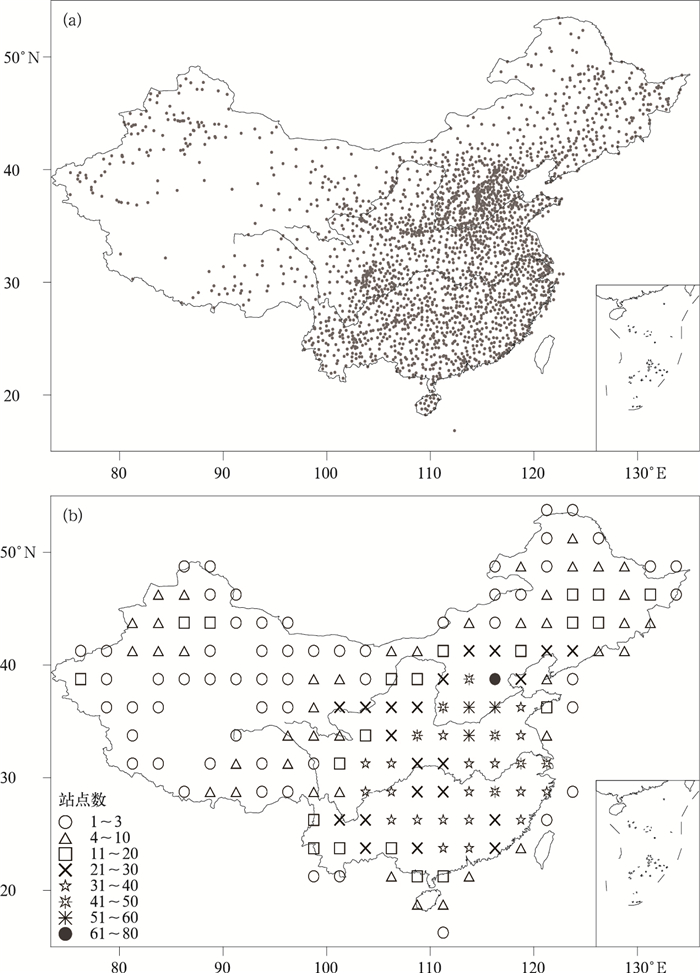
1 资料和方法

本文使用国家气象信息中心提供的经过质量检验和插补后的我国大陆区域2416个气象观测站点1966—1995年30年的气温和降水量资料集，站点分布见图 1a。我国大陆区域站点分布不均匀，以2.5°×2.5°经纬度网格为例，2416个站点分布在172个网格中 (图 1b中标注点为网格的中心点，下同)。华北平原、江淮和长江中下游地区站点密集，以38.75°N，116.25°E为中心的格点包含75个站点，而西部地区大多数网格中站点不超过4个，特别是青藏高原中西部和塔克拉玛干沙漠腹地站点分布稀疏。虽然在站点均匀性上有些问题，但该站网是目前我国密度最高的气象观测网络。在美国每隔180 km设置1个站点即可满足对气候变化监测的需要[13-14]，相当于2.5°×2.5°经纬网格中最多4个站点即可满足研究气候变化的需要。在大部分地区，2416个站点组成的站网格点包含的站点数超过4个。因此，本文认为由2416个气象观测站点组成的站网在大部分地区能够基本准确监测区域气候特征和气候变化信号。塔克拉玛干沙漠腹地地表类型单一，对站网密度的要求相对较低，而青藏高原中西部地区人迹罕至，部分地区无长时间的观测，这些地区尚无更好的器测资料。所以，设定2416个观测站点组成的站网为标准站网，但在我国西北地区西部和青藏高原，结果需进一步讨论。

图 1. 我国大陆气象观测站点分布 (a) 及2.5°×2.5°经纬度网格内包含站点数量 (b) Fig 1. Distribution of 2416-station (a) and the number of stations in each grid cell with the resolution of 2.5°×2.5°(b)

在某一地区，对比使用不同数量的站点所得的区域平均气候序列与标准站网所得序列之间的关系，可以得到该地区台站数量对站网监测气候变化信号能力的影响，并得到在保证某一监测能力前提下所需的最少站点数量，进而获得该地区的最优站网密度。考虑到气候变化研究既关心气候要素的变化趋势，又注重其年际和年代际波动，因此，使用两序列的相关系数表征气候变化信号的监测能力。保证站网对信号的监测能力主要是指最优站网所得网格区域气候要素序列与标准站网所得对应要素序列的相关系数高于某个数值 (例如，两个序列相关系数高于0.99)。参考Janis等[13]的方法，分析站点密度对站网监测能力的影响，具体步骤如下：

① 计算标准站网每个网格单元的区域平均气温距平和年降水量距平百分率。如无特殊说明，下文中气温、降水量均指年气温距平与年降水量距平百分率。

② 在每个网格单元内随机采样得到一个包含Ns个站点的子集站网 (1≤Ns≤N-1，其中N是在网格单元内的站点总数)。

③ 考虑到格点跨度较小，这里使用算术平均计算Ns站网的区域平均气温距平和降水距平百分率序列。例如，在某格点采样得到包含20个站点的子集站网，其在第i年的格点平均值为

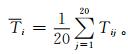
(1)

Ti为由Ns(这里Ns=20，1≤Ns≤N-1) 个随机选出的站点组成的子集站网在第i年的区域平均值，Tij为第j个站点的要素值。

④ 计算该Ns子集站网序列 (气温距平和降水距平百分率) 与标准站网序列的相关系数。不改变Ns的取值，重新进行随机采样，得到由不同站点组成的相同密度的站网，重复步骤③，计算Ns站网序列与标准站网序列的平均相关系数。以100次为例，利用式 (2) 计算任一Ns站网 (气温距平和降水距平百分率) 序列与标准站网序列的平均相关系数 (cM)，

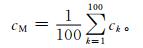
(2)

其中，100为蒙特卡罗Ns站点重采样的次数；ck为第k次采样序列与标准站网序列的相关系数。

⑤ 对所有可能的子集站点个数 (Ns=1, 2, …, N-1) 重复步骤③ 和④，得到各个网格站点数量与对应的cM。

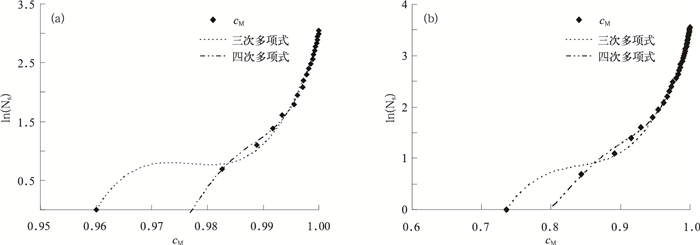
⑥ 分析cM与Ns的相互关系，寻找最适合的回归方程。分析多种回归方法的显著性和残差平方和后，发现Ns的对数与cM之间的一元三次多项式拟合效果最好。以网格37.5°~40°N，117.5°~120°E为例进行说明 (图 2)。

图 2. 子集站网气温序列 (a)、降水量序列 (b) 和标准站网序列的相关系数与站点数拟合图 Fig 2. The relationship of cM of temperature (a) and precipitation (b) to station number

计算选样站点数 (Ns) 的cM多项回归式：

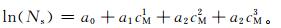
(3)

将cM值带入式 (3)，即可得到对应的网格内所需站点数量。就网格37.5°~40°N，117.5°~120°E的降水量来说，如果预设的目标是相关系数大于0.90，则布置3个或以上站点即可；但如果目标为相关系数大于0.95，则需要布置6个或以上站点。

2 不同网格情况

考虑到气候变化研究的空间尺度，选择2.5°×2.5°，2.5°×3.5°和5.0°×5.0°经纬度网格进行研究。

2.1 2.5°×2.5°网格情况

对我国大陆2.5°×2.5°经纬度网格内全部站点分别进行蒙特卡罗采样，计算获得子集对气候变化信号的监测能力与站点数量的关系。随站点密度逼近标准站网密度，对信号的监测能力逐渐升高，即对所有网格，随着子集站网序列与标准站网序列相关性提高，所需台站数量均将相应增加。由于降水量观测更易受局地地形等小尺度因素影响，同一个2.5°×2.5°的网格内相同要求降水量观测所需的站点数量远多于气温。

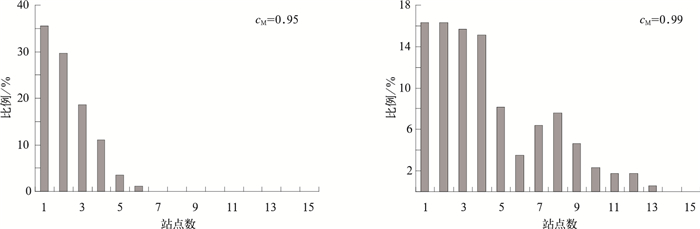
2.1.1 气温

分别按照不同的气温观测要求 (cM=0.95, cM=0.99) 计算各个网格所需站点数，得到全国各个格点所需的站点数的分布情况 (图 3)。

图 3. 满足不同气温观测要求时网格内所需站点数量所占比例分布 Fig 3. Frequency distributions for network meeting the goal of temperature monitoring

图 3显示，当cM=0.95时，35%的网格仅需要1个站就可以满足要求，30%左右的网格需要2个站，也就是说在每个格点中任意选择2个站，超过65%的子集站网所得格点值与标准站网所得格点值的相关系数不小于0.95；而当cM提高到0.99时，网格对站点数量的要求有明显提高，表现为要求达到4个以上站点的网格比例明显增大。考虑到当序列长度为30时，相关系数不低于0.570就可以通过0.001水平的显著性检验，因此，可以认为对于大多数格点来说1~3个站点就可以满足一般气温变化研究的需要。此外，需要注意的是，尚有部分格点对站点数量要求较高，图 4和图 5给出了各网格对站点密度要求的空间分布情况。

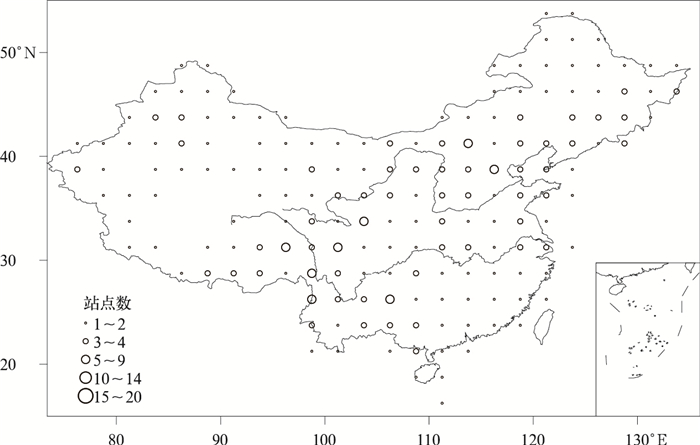
图 4. 1966—1995年气温观测满足cM=0.95时377个站点分布 Fig 4. Grid cell densities of 377-station network for satisfying temperature monitoring goal of cM=0.95 during 1966—1995g

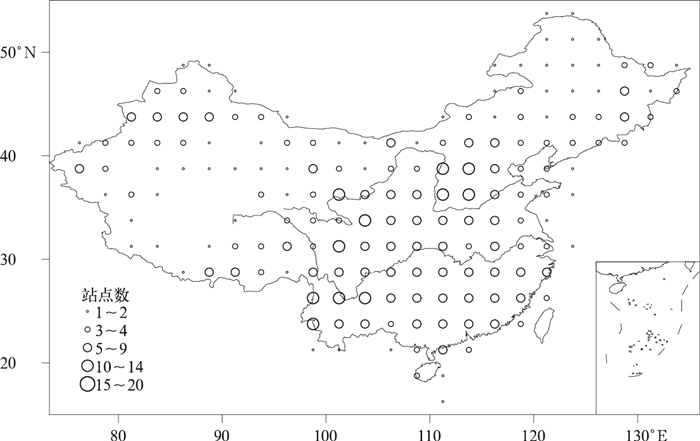
图 5. 1966—1995年气温观测满足cM=0.99时750个站点分布 Fig 5. Grid cell densities of 750-station network for satisfying temperature monitoring goal of cM=0.99 during 1966—1995

由图 4和图 5可以看出，大部分对站点数量要求较高的网格处于地势起伏剧烈的地区, 如四川盆地周边地区、横断山脉地区等。此外，当观测标准要求提高时，武夷山、黄土高原、秦岭、东南丘陵等地区对应的站点密度也有明显的提高，说明高精度的气候监测要求在地形条件复杂地区设置更密集的站网。

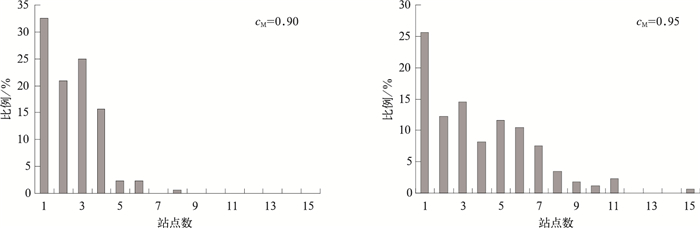
2.1.2 降水量

考虑到降水的局地性强，属于对台站间距要求最高的观测项目[7]，这里选择cM=0.95, cM=0.90分别进行分析。按照不同的精度要求计算各个网格所需站点数目，得到全国不同降水监测标准所对应的站点数量分布情况 (图 6)。

图 6. 满足不同降水量观测要求网格内所需站点数量所占比例分布 Fig 6. Frequency distributions for network meeting the goal of precipitation monitoring

图 6为降水量观测满足cM=0.90和cM=0.95时各个网格内站点数量占总站数 (标准站网台站数量) 百分比的分布情况。与气温的情况类似，当cM要求较低时，网格内站点密度要求较低，绝大部分可在4个以下；而当cM标准提高后，有更多网格对站点数量的要求明显提高，分布向高密度方向延伸，要求具备5~7个站的网格数量比较多。

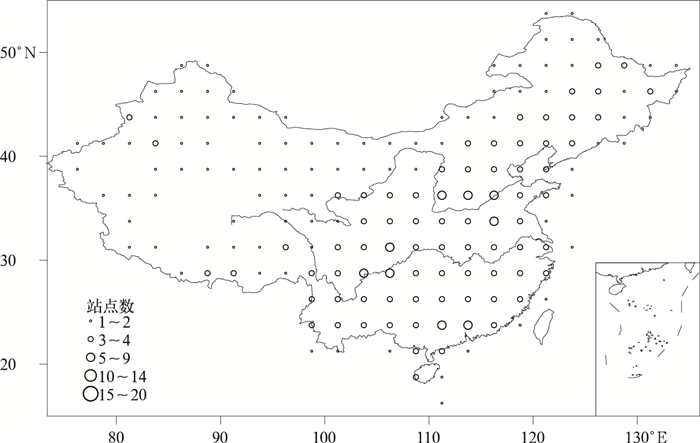
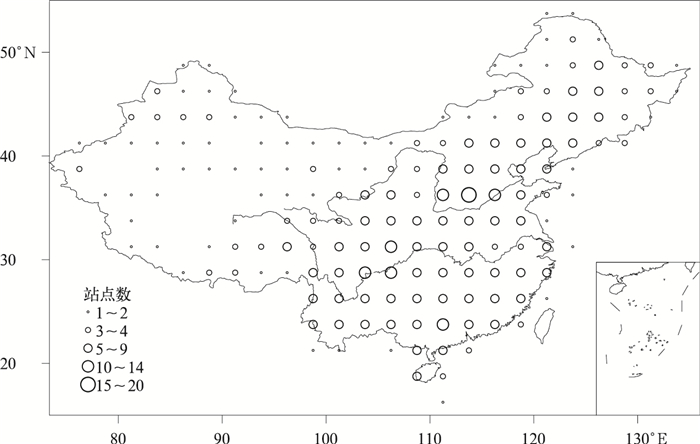
分析降水量观测各个网格单元在cM=0.95和cM=0.90的精度要求下所需站点密度的空间分布 (图 7和图 8)。在各种情况下，四川盆地东南部降水量观测对站点密度要求均较高。此外，太行山附近所需站点也较多。与气温观测对站点密度的要求分布相比，江南和华南地区降水对站点密度的要求要高一些。

图 7. 1966—1995年降水量观测满足cM=0.90时417个站点分布 Fig 7. Grid cell densities of 417-station network satisfying precipitation monitoring goal of cM=0.90 during 1966—1995

图 8. 1966—1995年降水量观测满足cM=0.95时670个站点分布 Fig 8. Grid cell densities of 670-station network satisfying precipitation monitoring goal of cM=0.95 during 1966—1995

2.2 大网格情况

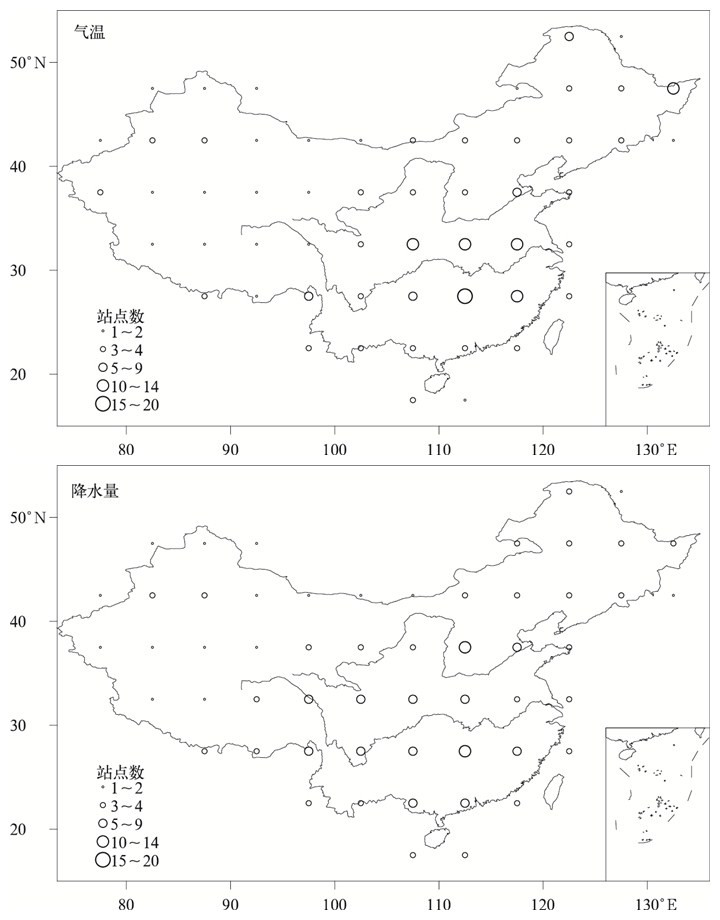
考虑到不同研究尺度对站点密度也会有不同的要求，对2.5°×3.5°和5.0°×5.0°经纬度网格情况下cM＞0.90时所需站点密度进行了分析，结果如图 9和图 10所示。

图 9. 1966—1995年观测满足cM=0.90时站点分布 (2.5°×3.5°) Fig 9. Grid cell densities of station network satisfying monitoring goal of cM=0.90 during 1966—1995(2.5°×3.5°)

图 10. 1966—1995年观测满足cM=0.90时站点分布 (5.0°×5.0°) Fig 10. Grid cell densities of station network satisfying monitoring goal of cM=0.90 during 1966—1995(5.0°×5.0°)

对气温资料进行2.5°×3.5°网格化时，若cM=0.90，则全国所需站点总数为307，站点密度要求较高的地区主要集中在四川盆地周边山区、黄土高原、东北东部山地、东南丘陵和山地等地区，其中长白山区、吕梁山区、秦岭山脉、青藏高原东缘等地要求的站网密度最高。降水量观测对站点密度的要求与气温较为相似，但多数地区所需的站点数量普遍比气温高，全国所需站点总数为353个，其中吕梁山区、太行山区、四川盆地、南岭山区及其岭南地区所需站点数量最多。

在5.0°×5.0°网格情况下，与东部其他地区相比，长江中下游地区，特别是江南西部，气温观测对站点密度要求较高，东北北部和青藏高原东南等区域要求的站点密度也较大，全国所需站点总数为262个。降水量观测所需的站点数量以长江流域和珠江流域为最高，华北和青藏高原东缘所需站点数量也较多，全国所需站点总数为245个。总的来说，在大网格情况下，气温与降水量观测对站点密度的要求比小网格时更为相似。

3 结论和讨论

本文对我国大陆地区不同气候变化监测能力要求下，不同尺度经纬度网格所需站点数量进行了分析，获得以下结果：

1) 随着对监测要求的下降，所需站点数迅速下降。以2.5°×2.5°网格为例，当要求子集站网气温序列与标准站网气温序列相关系数由0.99下降为0.95时，全国所需的站点数由750下降为377；当要求子集站网降水量序列与标准站网降水量序列的相关系数由0.95降为0.90时，全国所需的站点数由670降为417。

2) 随格点面积扩大，相同监测要求所需站点数下降。对2.5°×2.5°，2.5°×3.5°和5.0°×5.0°经纬度网格来说，全国所需的站点数均明显下降。

3) 对站点数量要求较高的区域多位于地势起伏剧烈或由山地向平原、高原过渡地带。对站点密度要求较高的地区主要集中在四川盆地周边山区、武夷山、黄土高原、秦岭、东南丘陵、东北东部山地等地区。这些地区地势复杂，区域相关性低，要求站点密度高，实际上是气候变率、变化空间异质性或空间差异性大的反映。

此外，需要注意的是，5°×5°网格中气温与降水量观测对站点密度的要求比小网格时更为接近，可能是研究尺度扩大抵消了一部分局地分量，相对来说更多反映大尺度的区域情况，但具体原因仍需进一步研究。

青藏高原中西部地区和塔克拉玛干沙漠中心地区各种类型的站点均较稀少，标准站网中的站点数量也不充分。对这些地区站点密度的需要还应结合其他方法做进一步分析；山区标准站网中站点也多数分布在谷底和山麓地区，较少设置在山坡或山顶，代表性不充分，如果能够采用更具代表性的标准站网，山区实际所要求的站点数量可能更多。

参考文献
[1] 任国玉, 初子莹, 周雅清, 等. 中国气温变化研究最新进展. 气候与环境研究, 2005, 10, (4): 701–716.
[2] 张人禾. 气候观测系统及其相关的关键问题. 应用气象学报, 2006, 17, (6): 705–710.
[3] Peterson T C, Daan H, Jones P D. Initial selection of a GCOS surface network. Bull Amer Meteor Soc, 1997, 78: 2145–2152. DOI:10.1175/1520-0477(1997)078<2145:ISOAGS>2.0.CO;2
[4] 周尚河. 全国高空资料质量控制和建库方法的研究. 应用气象学报, 2000, 11, (3): 364–370.
[5] 黄嘉佑, 刘小宁, 李庆祥. 中国南方沿海地区城市热岛效应与人口的关系研究. 热带气象学报, 2004, 20, (6): 713–722.
[6] 张强, 郭发辉, 许松. 全球地面天气报资料质量控制和数据集特征分析. 应用气象学报, 2004, 15, (增刊): 121–127.
[7] 王伯民. 基本气象资料质量控制综合判别法的研究. 应用气象学报, 2004, 15, (增刊): 50–59.
[8] 林学椿, 于淑秋, 唐国利. 北京城市化进展与热岛强度关系的研究. 自然科学进展, 2005, 15, (7): 882–886.
[9] 吴增祥. 气象台站历史沿革信息及其对观测资料序列均一性影响的初步分析. 应用气象学报, 2005, 16, (4): 461–467.
[10] Ren G Y, Chu Z Y, Chen Z H, et al. Implications of temporal change in urban heat island intensity observed at Beijing and Wuhan stations. Geophys Res Lett, 2007, 34: L05711. DOI:10.1029/2006GL027927
[11] Hubbard K G. Spatial variability of daily weather variables in the high plains of the USA. Agric Forest Met, 1994, 68: 29–41. DOI:10.1016/0168-1923(94)90067-1
[12] DeGaetano A T. Spatial grouping of United States climate stations using a hybrid clustering approach. Int J Climatol, 2001, 21: 791–807. DOI:10.1002/(ISSN)1097-0088
[13] Janis M J, Hubbard K G, Redmond K T. Station density strategy for monitoring long-term climatic change in the contiguous United States. J Climate, 2004, 17: 151–162. DOI:10.1175/1520-0442(2004)017<0151:SDSFML>2.0.CO;2
[14] Janis M J, Hubbard K G, Redmond K T. Determining the Optimal Number of Stations for the United States Climate Reference Network. Final Report to NOAA/NCDC, 2002.
[15] 赵瑞霞, 李伟, 王玉彬, 等. 空间结构函数在北京地区气象观测站网设计中的应用. 应用气象学报, 2007, 18, (1): 94–101.
[16] von Storch H, Zwiers F W. Statistical Analysis in Climate Research. Cambridge: Cambridge University Press, 1999.