2. 国家气象中心,北京 100081
2. National Meteorological Center, Beijing 100081
大气资料同化的一个重要特征是它所得到的分析场的各要素之间必须满足真实大气中最基本的动力平衡约束,例如,分析得到的风场和质量场在中高纬度地区大尺度自由大气中应满足准地转平衡关系[11]。在同化框架中引入变量之间的动力平衡约束不仅可以减小高频重力波对后续积分的影响,而且可以更加有效地利用观测信息,如可以利用风场的观测改进质量场的分析[2-3]。此外,对于变分同化而言,动力平衡约束的引入还可以改善目标函数极小化求解的预条件[4]。我国自主研发的数值天气预报系统GRAPES (Global/Regional Assimilation and PrEdiction System) 采用变分同化方案[5-6]。在目前已有的GRAPES模式面三维变分 (3D_Var) 同化系统中,对于动力平衡约束处理还比较粗糙,为提高同化分析效果,探索更加合理的平衡约束方案十分必要。
3D_Var系统的控制变量一般都采用旋转风、散度风、质量场和水汽4个要素,其中旋转风和质量场之间的配合是大气中最重要的平衡关系。关于这两个要素之间动力平衡约束的引入,世界各主要3D_Var系统有着不同的方法,但大体可以分为3类。第1类是利用动力气象学中推导出的简化平衡方程来约束两要素的协同变化,早期的美国国家气象中心 (NMC) 的变分方案中,便直接采用线性平衡方程来表达旋转风和质量场之间的平衡[7]。然而,当真实大气不能近似满足地转平衡关系时,如在近赤道地区和高空急流区,仍直接采用此类简化平衡方程就会产生较大的偏差[2-8]。此外,现代同化系统多是在与预报模式一致的地形追随坐标面上分析控制变量,平衡方程在这样的坐标面上展开会涉及地形,难于求解。第2类方案是采用线性回归方法直接统计出旋转风和质量场之间的平衡约束关系。该方案操作简单,并且在地转关系不适用地区可以有效限制风场和质量场的耦合程度,使这些地区风场和质量场之间的同化分析更加独立,这在欧洲中期数值预报中心 (ECMWF) 的3D_Var方案[9]以及WRF 3D_Var系统[10]中都有着成功应用。第3类方案是将前两者结合起来,仍采用简化平衡方程做动力约束,但加入线性回归以缓解特定地区平衡方程不适用的问题,MM5 3D_Var系统[11]和英国气象局的3D_Var系统[12]就采用了这样的方案,也取得了较好的分析效果。
早期的同化系统一般只考虑旋转风和质量场之间的配合[7-8], 然而20世纪90年代中期以来的研究表明,在边界层等特定区域,旋转风和散度风之间的动力平衡约束也不容忽视[9-10]。由于边界层湍流运动活跃,摩擦力不可忽视,使得该层中的天气尺度涡旋总伴随着较强的辐合、辐散运动。以北半球边界层为例,逆时针旋转气流一般伴随着内流的辐合运动,顺时针旋转的气流一般伴随着外流的辐散运动,这样的辐合、辐散运动是大气垂直运动的重要原因,也是产生天气变化的重要因素[13]。因此,在同化中有必要引入旋转风和散度风之间的动力平衡约束,这种约束一般采用线性回归的方法加以引入[9-10]。
我国的GRAPES模式面3D_Var系统是在等压面3D_Var系统的基础上发展而来的。在等压面3D_Var系统中动力平衡约束的引入采用的是前面所述的第1种方法,即采用线性平衡方程来约束旋转风和质量场之间的平衡关系[14]。然而,模式面3D_Var系统的分析在与模式一致的高度地形追随坐标面上进行,平衡方程难于求解。因而,采取了一种折中方案引入动力平衡约束:先将模式面上的信息插值到一组参考等压面上,在等压面上求解平衡方程,然后再将平衡信息插回到模式面上[15]。这样的方案涉及多次垂直插值,并且在大地形、极地等地区会出现外插的情况,误差较大。此外,如前文所述,在近赤道和高空急流区,线性平衡方程描述的平衡关系与真实大气相差较大,且现有方案中也未引入旋转风和散度风之间的平衡约束。为解决这些问题,本文采用统计方法求解控制变量间的动力平衡约束,直接在模式面上统计出旋转风和质量场之间以及旋转风和散度风之间的平衡关系,完善变量之间的分析平衡,同时也避免垂直方向的插值,减少误差的引入。
1 变量预处理和动力平衡约束为便于同化系统和预报模式的耦合,GRAPES模式面3D_Var系统的分析变量x采用的是模式预报变量:水平风 (u, v),Exner函数 (以下称为无量纲气压,π) 以及水汽 (比湿或相对湿度,用q表示)。这些变量的分布与预报模式一致,垂直坐标采用高度地形追随坐标,水平离散采用Arakawa-C方案,垂直离散采用Charney-Phillips交错方案[16-18]。
由于x的各变量之间彼此相关,为简化变分问题,引入流函数ψ(表征旋转风) 和势函数χ(表征散度风) 代替 (u, v) 表示水平风场,并结合π和q构成3D_Var系统的控制变量。在此基础上,进一步将χ和π拆分成平衡部分和非平衡部分,具体可定义为[9-11]

|
(1) |
式 (1) 中, χu,πu分别表示χ,π的非平衡部分,M,N,L是平衡算子。GRAPES 3D_Var系统采用ψ,χu,πu以及q作为其非平衡控制变量 (记为xc)。从非平衡控制变量xc向分析变量x的转换称作物理变换[11]:
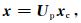
|
(2) |
式 (2) 中,Up称为物理变换算子。根据式 (1),并结合 (ψ, χ) 和 (u, v) 之间的转换关系,Up可以具体表达为
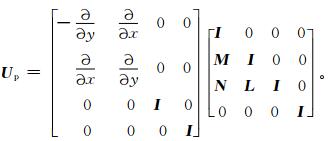
|
(3) |
式 (3) 中,I为单位矩阵。通过物理变换算子Up,相互之间相关的分析变量x转换成了相互之间独立的非平衡控制变量xc。但每一个非平衡控制变量自身在不同空间格点上仍存在相关,继续做空间变换:
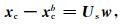
|
(4) |
式 (4) 中,xcb是xc的背景场值,Us是空间变换算子。如果构造Us使它满足
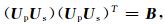
|
(5) |
其中,B是分析变量x的背景误差协方差矩阵。那么,式 (4) 中得到的新的变量w的每一个元素将各自独立,并满足标准正态分布[19]。有关空间算子Us的构造细节可参见相关文献[20]。
上述的变量变换综合起来就是GRAPES模式面3D_Var系统的变量预处理过程,它极大简化了变分问题。在此基础上,GRAPES模式面3D_Var系统的目标函数可表示为
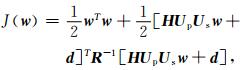
|
(6) |
式 (6) 中,R是观测误差协方差矩阵,H是切线性观测算子,d是观测空间中背景场和观测场的差值,其余符号定义如前。
本文所要研究的GRAPES 3D_Var系统中的动力平衡约束就是式 (1) 中的平衡算子M, N, L,它们表达了不同控制变量之间的动力学平衡关系。更进一层,根据式 (5) 的定义,这些平衡算子实际上是抽取了背景误差协方差矩阵B中的平衡关系,反映的是不同控制变量背景误差的交叉协相关。
从物理意义上来说,M, N, L算子分别反映了旋转风和散度风之间、旋转风和质量场之间以及非平衡散度风和质量场之间的动力学约束关系。由于大尺度自由大气在赤道外地区具有准地转和准水平无辐散的特征[13],因此实际大气中算子N表达的动力平衡约束最为重要。而如引言中所提到的,M算子的影响主要在边界层,对模式底层风场分析重要。此外,有研究表明L算子的影响主要体现在近赤道地区,对赤道外地区影响很小[9]。
现有的GRAPES模式面3D_Var系统采用线性平衡方程来表达算子N,算子M,L未予以考虑[20]。本文则采用统计方法求解M和N算子。对于L算子,由于其影响主要局限于热带地区,而且目前GRAPES模式给出的该地区的预报误差样本不理想,初步统计发现,若考虑该算子,容易引入虚假的非平衡散度风和质量场的相关。因此,本研究工作中暂时仍不考虑L算子,今后条件成熟时再进一步研究。
2 动力平衡约束的统计求解由于动力平衡约束反映了不同控制变量背景误差之间的交叉协相关关系,因此可以通过一组采用NMC方法[7, 21]估计得到的背景误差样本来统计M,N。下面给出具体的统计方案和结果。
2.1 资料业务运行的3D_Var系统常采用数值模式的6 h短期预报结果作为背景场,因此背景场的误差又常被称作预报误差,本文使用NMC方法估算控制变量的预报误差值。即采用GRAPES全球模式预报到同一时刻的48 h和24 h的预报结果的差值作为预报误差的估计:
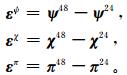
|
(7) |
式 (7) 中,ε是变量预报误差估计的样本值,上标48和24分别指48 h预报和24 h预报结果。模式水平分辨率取为1°×1°,垂直整层数取为37。此时,根据GRAPES垂直方向的离散方案[18],u,v被定义在半整数层上,共36层,π也被定义在半整数层上,但比水平风多两层,共38层。后续统计工作是在u,v和π均有定义的36层半整数层上进行的 (下文提到的模式面层次,均指半整数层的层次)。
由于GRAPES模式的预报变量中并不包括流函数ψ和势函数χ,因而需要通过u,v转换得到。具体做法:首先在Arakawa-C网格上利用中央差分将u,v转变为涡度和散度,转换公式采用球面坐标系下的形式[22];再将涡度转换成流函数,散度转换成势函数,为提高精度,这里可以采用球面谱方法求解[23]。
本文选取2009年12月1日—2010年2月28日每天00:00(世界时,下同) 和12:00起报的24 h和48 h模式面预报结果,先作模式变量和控制变量之间的转换,再根据式 (7) 计算出各控制变量的178个预报误差样本进入到下面的统计工作中去。同时引入00:00和12:00的预报可以减少模式日变化的影响。此外,经初步研究发现,统计得到的平衡算子对于样本数的选择具有一定的敏感性,样本越多,平衡算子的空间分布越平滑,但当样本达到一定个数以后 (如60以上时),统计结果基本保持稳定。
2.2 统计方案由于大气中旋转风和质量场之间具有线性关系,因此可以使用线性回归统计平衡算子N[10];旋转风和散度风之间的关系较为复杂,但采用线性回归也能将散度风中的线性平衡部分分离出来,尽可能减少非平衡控制变量之间的相关程度。因此,本文采用线性回归的方法计算平衡算子M和N。
考虑到科氏力沿纬度的变化,平衡算子需要在径向上变化;而大气的垂直分层,使得平衡算子也应按高度变化。此外,就真实大气而言,动力平衡约束在同一纬圈上也会有变化,但变化相对较小,且主要集中于大气底层复杂地形处,对全球预报影响有限;并且,如要在统计方案中将纬向上的变化考虑进来,需要大大增加样本的数量。因此,统计方法求解动力平衡约束的实际应用中一般仅使平衡算子随纬度和高度变化[9-10, 12]。
在这样的前提下,本文在模式面上逐层、逐纬圈求解M,N,具体公式如下:
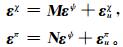
|
(8) |
式 (8) 中,符号定义如前。在纬圈上求解式 (8) 时,可以采用两种方案,一种是将纬圈上所有格点上的预报误差时间序列累加在一起,构成一个总的预报误差样本,然后根据式 (8) 求出该纬圈上的回归系数;第2种方案是先在该纬圈360个经纬格点上,依据其自身的预报误差时间序列,逐个做线性回归,求出360个回归系数,再对这些系数作纬向平均,将这个纬向平均值作为该纬圈上的平衡系数。通过试验发现,第2种方法比第1种方法略好,可以减少噪音的引入。因此,采用第2种方案求得平衡算子,进入下一步的工作。
采用式 (8) 逐层、逐纬圈统计得到M,N算子以后,GRAPES模式面3D_Var系统的物理变换Up就可以直接在模式面上进行,无需像原方案那样引入参考等压面来求解线性平衡方程,简化了计算,也减少了误差引入。
2.3 统计结果为了直观地认识统计得到平衡算子M,N究竟如何划分εχ和επ的平衡部分及非平衡部分,可以引入方差解释率来描述平衡部分占总体的比例。以επ的回归方程为例,其方差解释率定义为
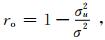
|
(9) |
其中,σu2是εuπ的样本方差,σ2是επ的样本方差,εχ情形类似。
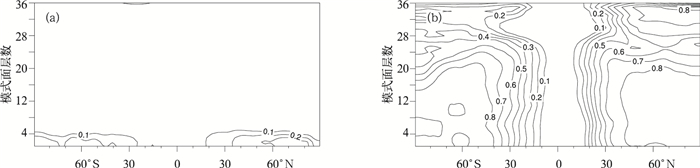
图 1给出了势函数和无量纲气压的平衡部分对总体的方差解释率。图 1的纵坐标是控制变量所在的模式面的层数。为符合气象习惯,方便理解,表 1给出了图 1垂直坐标中的各层模式面对应的大致气压值。
|
|
| 图 1. 变量平衡部分对总体方差解释率的纬向平均分布(a) 势函数,(b) 无量纲气压 Fig 1. Zonal average of the explained variance ratios of velocity potential (a) and dimensionless pressure (b) | |
|
|
表 1 12月、1月和2月GRAPES模式面对应气压 Table 1 Roughly corresponding pressure values of GRAPES model levels in Dec, Jan and Feb |
图 1a给出的是势函数χ的平衡部分对其全量的方差解释率。从图 1a中可以看出,方差解释率的大值区主要集中于中高纬度地区模式低层 (第4层向下),解释率为0.1~0.4,北半球的解释率略大于南半球。这样的分布说明,旋转风和散度风的配合主要集中在中高纬度地区边界层。根据天气学原理,边界层湍流运动活跃,能引起较强的地转偏差,中高纬度地区常见的天气尺度涡旋系统在该层中一般都伴随着较强的辐合、辐散运动,旋转风和散度风的联系在该区域相对比较紧密[13]。
图 1b给出的是无量纲气压的平衡部分对全量的方差解释率。由图 1b可知,方差解释率由赤道向两极逐步增大,其大值区 (≥60%的部分) 主要位于第24层 (约153 hPa) 以下的中高纬度地区 (30°N以北,30°S以南)。图 1b中南半球模式高层解释率出现了明显下降,这与其他同化中心给出的结果类似,研究表明,模式高层预报效果不理想,噪音过大可以部分解释这一现象[9-10, 12]。
需要指出的是,采用线性回归方法求得的动力平衡约束,更多地反映特定模式本身的预报变量之间的耦合程度,与实际大气中变量间的配合还有一定差距。但是由于现代数值模式发展水平已经很高,模式预报变量之间的关系越来越接近实际大气本身的状况,因而各个同化预报中心统计得到的控制变量平衡部分对总体的方差解释率也越来越接近。本文图 1给出的结果就与英国气象局3D_Var系统[24]以及WRF 3D_Var系统[10]统计出的结果十分接近。
3 数值试验为检验由统计方法得到的控制变量间动力平衡约束的合理性,并比较其与原方案的不同,本文接下来从两个方面进行考察,一是随机扰动试验,二是单点试验。
3.1 随机扰动试验在同化分析系统中,背景误差协方差矩阵B的给定,对最终的分析效果有着非常重要的影响[1]。本文第1章已讨论过,在GRAPES变分同化系统中B矩阵不是直接给定的,而是通过物理变换算子Up和空间变换算子Us隐式表达的。而本文致力于采用统计方法求解控制变量之间的动力平衡约束,从而重新构造了物理变换算子Up,这样的变动对B矩阵到底会产生什么样的影响,需要仔细评估。借鉴欧洲中期数值预报中心的做法,可以采用随机扰动法[25]模拟同化系统中有效的B矩阵,用以评估Up算子变动前后,系统中有效B矩阵的变化情况,该方法基本公式为
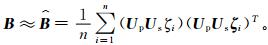
|
(10) |
式 (10) 中,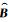
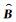
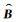
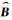
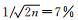
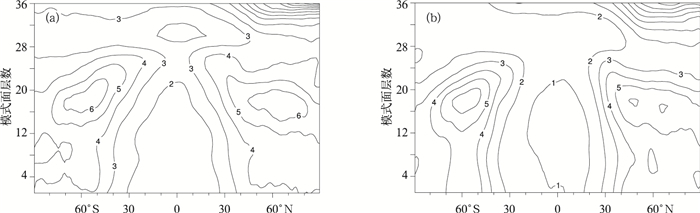
图 2a,2b分别给出了随机扰动法模拟出的原方案和新方案中,无量纲气压的有效背景误差均方差的纬向平均分布。两者的分布形势十分接近,图 2a的结果在整体上略大于图 2b。但进一步观察可以发现,在近赤道地区以及对流层高层至平流层的强风区,原方案的数值比新方案要大得多。其可能原因是在这些地转关系不适用地区,原方案仍利用线性平衡方程约束流函数和无量纲气压的协同变化,可能与实际大气中风场和质量场之间的真实耦合程度相差较大。
|
|
| 图 2. 随机扰动方法模拟的无量纲气压的背景误差均方差的纬向平均分布 (单位:10-4) (a) 原方案,(b) 新方案 Fig 2. Zonal average of simulated background error standard deviations of dimensionless pressure in the original scheme (a) and the new scheme (b)(unit: 10-4) | |
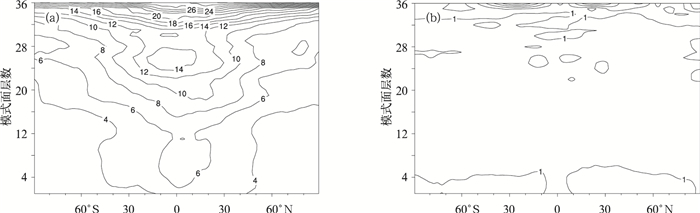
图 3a给出的是随机扰动方法模拟出的新方案中势函数的有效背景误差均方差的纬向平均分布,图 3b则是其中的平衡部分。比较图 3a和3b,势函数的平衡部分在边界层仍不容忽视,这与图 1a给出的散度风平衡部分的方差解释率可以相互印证。原方案中势函数背景误差均方差的模拟结果,与图 3a基本一致,但原方案中没有图 3b所示的与流函数的平衡部分。
|
|
| 图 3. 随机扰动方法模拟的新方案中势函数背景误差均方差的纬向平均分布 (单位:106m2·s-1) (a) 势函数全量,(b) 势函数的平衡部分 Fig 3. Zonal average of simulated background error standard deviations of velocity potential (a) and its balance part (b) in the new scheme (unit: 106m2·s-1) | |
3.2 单点试验
采用新方案,利用统计方法求解动力平衡约束,对同化分析结果的影响比较难于分析。当观测多于1个时,最终的分析结果是对观测增量 (观测值与分析值之差) 的非常复杂的加权平均,涉及的影响因素很多。而单点观测试验比较简单,它可以有效反映同化系统在所取单点周围误差信息的给定情况。
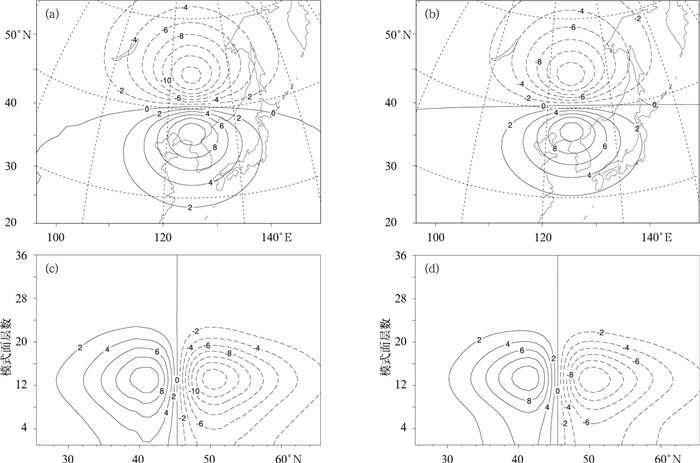
新方案与原方案相比,最主要的区别在于流函数和无量纲气压之间动力平衡约束求解方法不同。图 4给出了在中高纬度地区对流层中层放置一个理想风场u的观测,所强迫出的无量纲气压π的分析增量。单点位置在45.5°N, 125.5°E,模式面第12层,且u观测比背景场大5 m·s-1(向东)。图 4a, 4b分别给出了原方案和新方案中π的分析增量在模式面第12层上的水平分布;图 4c,4d则分别给出了两方案中π的分析增量在125.5°E处的经向-垂直剖面图。比较发现,该单点观测在新方案中强迫出的π分析增量与原方案几乎一致。说明在地转关系成立较好的区域,新方案与原方案中风场和质量场的协同变化程度基本一致。
|
|
| 图 4. 理想u观测 (高出背景场5 m·s-1) 位于模式面第12层45.5°N, 125.5°E时强迫出的无量纲气压分析增量 (单位:10-5) (a) 原方案水平分布,(b) 新方案水平分布,(c) 原方案经向垂直分布,(d) 新方案经向垂直分布 Fig 4. Dimensionless pressure increments generated by a simulated u component wind observation on the 12th model level at 45.5°N, 125.5°E which is 5 m·s-1stronger than background wind (unit: 10-5) (a) horizontal distribution of the original scheme, (b) horizontal distribution of the new scheme, (c) meridional section of the original scheme, (d) meridional section of the new scheme | |
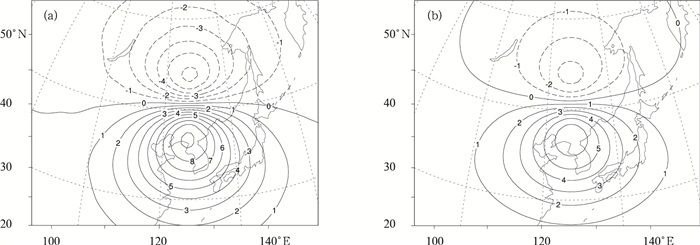
如果将图 4中的单点观测移至模式面第24层,其余设置不变,在这新的位置其强迫出的π增量的水平分布由图 5给出。新的位置恰好处于高空急流区,实际风为超地转风。比较图 5a和图 5b可以发现,原方案中π的分析增量要明显大于新的方案。这种现象出现的可能原因是在超地转的高空急流区,原方案仍采用了线性平衡方程来约束风场和质量场的协同变化部分,这与此处实际大气风场和质量场的配合程度不相匹配。
|
|
| 图 5. 理想u观测 (高出背景场5 m·s-1) 位于模式面第24层的45.5°N,125.5°E时强迫出的无量纲气象分析增量水平分布 (单位:10-5)(a) 原方案,(b) 新方案 Fig 5. Dimensionless pressure increments generated by a simulated u component wind observation on the 24th model level at 45.5°N, 125.5°E which is 5 m·s-1stronger than background wind (unit: 10-5) (a) horizontal distribution of the original scheme, (b) horizontal distribution of the new scheme | |
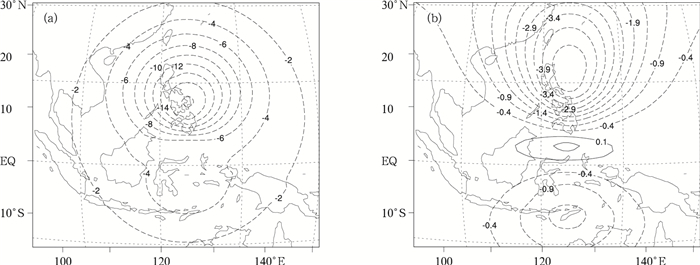
近赤道地区,由于科氏参数比中高纬度地区要小1~2个量级,对于天气尺度系统,地转关系不成立。为比较这一地区新方案和原方案的不同,将图 4中的单点风场观测移至5.5°N, 125.5°E,垂直层次不变,理想u观测仍比背景场大5 m·s-1(向东)。图 6a, 6b分别给出了此单点在原方案和新方案强迫出的π增量的水平分布。从图 6可以看出,新方案中π增量在数值上要远小于原方案,说明新方案中风场和质量场的分析在近赤道地区要更加的独立,两者的耦合程度较小。
|
|
| 图 6. 理想u观测 (高出背景场5 m·s-1) 位于模式面第12层的5.5°N,125.5°E时强迫出的无量纲气压分析增量的水平分布 (单位:10-6)(a) 原方案,(b) 新方案 Fig 6. Dimensionless pressure increments generated by a simulated u component wind observation on the 12th model level at 5.5°N, 125.5°E which is 5 m·s-1stronger than background wind (unit:10-6) (a) horizontal distribution of the original scheme, (b) horizonal distribution of the new scheme | |
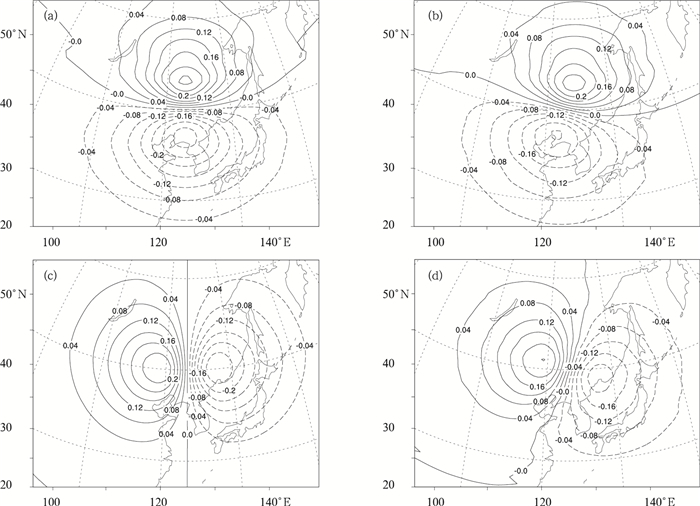
新方案与原方案相比,还有一点不同在于新方案引入了流函数和势函数之间的平衡,这在原方案中没有。图 7给出了模式面第1层,在45.5°N,125.0°E放置一个理想气压观测,使其高出背景场1 hPa,所强迫出的u,v风场分析增量的水平分布。其中图 7a,7c是原方案的分析结果,图 7b,7d则是新方案中的分析结果。比较这两组分析,可以发现新方案中,风场相对于经纬线发生了倾斜,而原方案中风场基本呈对称分布。这种差异说明,新方案在引入流函数和势函数的动力平衡约束之后,近地面质量场的观测信息不仅可以像原方案一样强迫出旋转风分量,而且可以通过流函数和势函数的平衡算子M进一步强迫出散度风的分量。
|
|
| 图 7. 理想气压观测 (高出背景场1 hPa) 位于模式面第1层45.5°N,125.0°E时强迫出的水平风场u, v的分析增量水平分布 (单位:m·s-1) (a)原方案u增量,(b) 新方案u增量,(c) 原方案v增量,(d) 新方案v增量 Fig 7. Wind increments generated by a simulated pressure observation on the first model level at 45.5°N, 125.0°E which is 1 hPa higher than the background (unit:m·s-1) (a)u increment of the original scheme, (b)u increment of the new scheme, (c)v increment of the original scheme, (d)v increment of the new scheme | |
4 总结和讨论
在资料同化方案的框架中,不同变量之间的动力平衡约束十分重要。本文针对GRAPES模式面3D_Var系统,采用线性回归统计求解流函数和无量纲气压间的动力平衡约束,代替原有方案中定义在参考等压面上的线性平衡方程;并同样采用线性回归的方法补充了原方案中所没有的流函数和势函数之间动力平衡约束。在此基础上,通过随机扰动试验和单点试验对比了新方案和原方案的差异。分析表明:
1) 新方案直接在模式面上统计得到控制变量之间的动力平衡约束,使得同化系统中的物理变换可以直接在模式面上进行,无需引入参考等压面来求解线性平衡方程,简化了计算,也避免了模式面和等压面之间反复插值,减少误差的引入。
2) 统计得到的流函数和无量纲气压之间的动力平衡约束在中高纬度地区对流层顶以下最强,在地转关系不适用的近赤道以及高空急流区减弱。而统计得到的流函数和势函数之间的动力平衡约束主要集中于中高纬度地区边界层。
3) 在满足地转关系较好的区域,新方案和原方案的单点试验结果差别很小;而在地转关系不适用区域,新方案可以有效减小风场和质量场之间的耦合程度,使得两者的同化分析在这些地区变得更加独立。
4) 由于本研究补充考虑了旋转风和散度风之间的动力平衡约束,使得边界层风场分析结果中包含了散度风分量,完善了近地面层风场分析的框架。
本研究目前只考虑了流函数和势函数、流函数和无量纲气压之间的动力平衡约束,由于模式噪音过大, 非平衡势函数和无量纲气压之间的相关目前仍未考虑。在今后的研究中,如果能找到较好方式滤除噪音的影响,可以考虑将这部分动力平衡约束引入。此外,本研究目前采用的数值试验都是理想试验,更加全面地了解新方案对于同化和模式预报的影响,还需要作更多测试,例如加入同化预报循环试验。通过更多的试验结果反馈可以不断修正已有方案,达到更好的同化效果。
| [1] | Daley R. Atmospheric Data Analysis. Cambridge: Cambridge University Press, 1991: 107–118. |
| [2] | Kalnay E. Atmospheric modeling, data assimilation and predictability. Cambridge: Cambridge University Press, 2003: 186–190. |
| [3] | Lönnberg P, Hollingsworth A. The statistical structure of short-range forecast errors as determined from radiosonde data Part Ⅱ: The covariance of height and wind errors. Tellus, 1986, 38A: 137–161. DOI:10.1111/tela.1986.38A.issue-2 |
| [4] | Courtier P, Talagrand O. Variational assimilation of meteorological observations with direct and adjoint shallow-water equations. Tellus, 1990, 42A: 531–549. DOI:10.3402/tellusa.v42i5.11896 |
| [5] | 薛纪善. 新世纪初我国数值天气预报的科技创新研究. 应用气象学报, 2006, 17, (5): 602–610. |
| [6] | 曾智华, 马雷鸣, 梁旭东, 等. MM5数值预报引入GRAPES三维变分同化技术在上海地区的预报和检验. 应用气象学报, 2004, 15, (5): 534–542. |
| [7] | Parrish D F, Derber J C. The national meteorological center's spectral statistical interpolation analysis system. Mon Wea Rev, 1992, 120: 1747–1763. DOI:10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2 |
| [8] | Lorenc A. A global three-dimensional multivariate statistical interpolation scheme. Mon Wea Rev, 1981, 109: 701–721. DOI:10.1175/1520-0493(1981)109<0701:AGTDMS>2.0.CO;2 |
| [9] | Derber J, Bouttier F. A reformulation of the background error covariance in the ECMWF global data assimilation system. Tellus, 1999, 51A: 195–221. |
| [10] | Wu W S, Purser R J, Parrish D F. Three-dimensional variational analysis with spatially inhomogeneous covariances. Mon Wea Rev, 2002, 130: 2905–2916. DOI:10.1175/1520-0493(2002)130<2905:TDVAWS>2.0.CO;2 |
| [11] | Barker M D, Huang W, Guo Y R, et al. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon Wea Rev, 2004, 132: 897–914. DOI:10.1175/1520-0493(2004)132<0897:ATVDAS>2.0.CO;2 |
| [12] | Lorenc A, Ballard S P, Bell R S, et al. The Met. Office global three-dimensional variational data assimilation scheme. Q J R Meteorol Soc, 2000, 126: 2991–3012. DOI:10.1002/(ISSN)1477-870X |
| [13] | 朱乾根, 林景瑞, 寿绍文, 等. 天气学原理和方法. 北京: 气象出版社, 2000: 22–59. |
| [14] | 庄世宇, 薛纪善, 朱国富, 等. GRAPES全球三维变分同化系统——基本设计方案与理想试验. 大气科学, 2005, 29, (6): 872–884. |
| [15] | 马旭林, 庒照荣, 薛纪善, 等. GRAPES非静力数值预报模式的三维变分同化系统的发展. 气象学报, 2009, 67, (1): 50–60. DOI:10.11676/qxxb2009.006 |
| [16] | 陈德辉, 杨学胜, 张红亮, 等. 多尺度非静力通用模式框架的设计策略. 应用气象学报, 2003, 14, (4): 452–461. |
| [17] | 黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现. 应用气象学报, 2005, 16, (3): 374–384. DOI:10.11898/1001-7313.20050312 |
| [18] | 陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17, (6): 773–777. DOI:10.11898/1001-7313.20060614 |
| [19] | Bannister R N. A review of forecast error covariance statistics in atmospheric variational data assimilation. Ⅱ: Modelling the forecast error covariance statistics. Q J R Meteorol Soc, 2008, 134: 1971–1996. DOI:10.1002/qj.v134:637 |
| [20] | 薛纪善, 陈德辉. 数值预报系统GRAPES的科学设计与应用. 北京: 气象出版社, 2008: 6–11. |
| [21] | Bannister R N. A review of forecast error covariance statistics in atmospheric variational data assimilation. Ⅰ: Characteristics and measurements of forecast error covariances. Q J R Meteorol Soc, 2008, 134: 1951–1970. DOI:10.1002/qj.v134:637 |
| [22] | 成秋影. 天气分析和诊断方法. 北京: 气象出版社, 1992: 152–156. |
| [23] | 沈桐立, 田永祥, 葛孝贞, 等. 数值天气预报. 北京: 气象出版社, 2003: 267–293. |
| [24] | Ingleby N B. The statistical structure of forecast errors and its representation in the met office global 3-D variational data assimilation scheme. Q J R Meteorol Soc, 2001, 127: 209–231. DOI:10.1002/(ISSN)1477-870X |
| [25] | Andersson E, Fisher M, Munro R, et al. Diagnosis of background errors for radiances and othe observable quantities in a variational data assimilation scheme, and the explanation of case of poor convergence. Q J R Meteorol Soc, 2000, 126: 1455–1472. DOI:10.1256/smsqj.56511 |
 2012, 23 (2): 129-138
2012, 23 (2): 129-138



