近年来，我国学者非常关注气象观测数据质量，特别是地面气象数据，各种数据质量控制方法在气象业务、科研和服务中得到了一定应用。如任芝花等^[1]、王海军等^[2]、陶士伟等^[3]、封秀燕等^[4]在自动气象站的实时资料质量控制方面进行了研究，并设计了相应业务系统；廖捷等^[5]对我国飞机观测气象资料进行了质量控制；任芝花等^[6-8]对全球历史地面天气报资料数据集、1971—2000年我国地面700多个基准基本站月气候资料进行了质量检查。国外在气象数据质量控制和评估方面比我国开展要早，近年来取得了不少成果^[9-14]。

由于在气候诊断分析、气候变化研究中，日气温数据是非常重要的基本资料，如我国各区域气象中心正在实施的“区域气候变化评估报告编制”工作，就需要高质量的历史逐日气温数据。然而目前我国对于日气温数据的质量控制基本采用传统方法，使得隐含在历史气温数据中的错误没有得到系统和全面的检查，影响其应用，所以开展新型数据质量控制方法研究很有必要。为此本文探讨两方面内容：一是设计基于线性回归数据估计方法的质量检查算法 (简称线性回归质量检查算法)，二是在该检查算法的基础上，研制综合一致性数据质量控制方法，对华中区域三省的历史日气温数据进行质量控制，以提高数据质量。

本文研究所使用的数据为1961—2009年华中区域三省251个站日平均气温、最高气温、最低气温3个要素，并应用日降水量和日照时数作为参考要素，其中河南省有105个站，湖北省有71个站，湖南省有75个站。

上述资料来自各省气象档案馆的信息化资料。这些资料的数字化工作大体可分为3个阶段：① 建站到20世纪90年代中期以前的资料，由人工首先从纸质报表输入到卡片或纸带，然后再转化成信息化资料；② 20世纪90年代中期到2003年前后，该阶段的资料由基层台站直接数字化后，按月上报到省级资料处理部门；③ 自动气象站阶段，从21世纪初开始我国陆续用自动站取代地面人工观测，其数据从采集开始就已数字化。所以本文所使用的资料绝大部分 (自动站除外) 都经过了人工观测、记录、抄录以及计算机录入、数据格式转换多个环节，所以不可避免地存在错误数据。这些数据虽已经过极值检查、内部一致性检查以及统计学检查等质量控制方法的检查，但对于与正确观测数据相差不大的可疑数据 (如相差3℃左右) 上述方法检查效果大都不理想。

气象资料质量控制方法中的空间一致性检查是较常用的方法。该方法的理论基础是气象要素在空间分布具有相关性，即空间距离较近的气象站点比距离较远的站点其特征值具有更大的相似性。空间一致性检查首先进行数据的空间插值，然后比较插值的估计值与观测值来实现数据的质量控制功能，其中使用较多的方法为空间回归检查方法^{[9-11, 15-16]}。

下面讨论的基于线性回归数据估计方法的质量检查算法 (即线性回归质量检查算法)，也包含空间一致性检查内容。该算法的思路是利用待检站与邻近站资料建立回归模型估计待检站数据，再通过观测值与估计值的差异，判断观测数据的质量。

根据文献[17]，将被检站数据作为估计量，邻近站资料为因子，可建立多元线性回归模型：

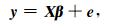
(1)

式 (1) 中，y，β，e为向量，分别为被检站数据、待估计的参数和随机变量；X为因子矩阵，表示邻近站资料。通过取样，对回归模型 (1) 进行估计，即可得到估计被检站气温的多元线性回归方程：

(2)

式 (2) 中，b₀，b₁，…，b_p为回归系数，是向量β的估计；x₁，x₂，…，x_p为邻近站气温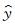；为被检站估计值; p为邻近站数。本文采用最小二乘法求解回归模型的系数。

求解回归模型的样本数据选取方法采用文献[18]的滑动优选法，即样本数据为被检日所在年前后若干年的同期资料。如估计1981年5月1日最高气温，则选择被检站以及邻近站4月16日—5月16日 (1979—1983年) 共5年每年31 d的最高气温数据作为样本数据 (不含1981年5月1日数据)，建立模型并求解回归系数，利用邻近站1981年5月1日的数据，通过式 (2)，估计1981年5月1日的最高气温。为简化取样方法，当估计时间边界上的数据 (如估计1月1日，则样本数据的日期要跨年) 时，数据选样采用文献[18]的方法。其中邻近站是选取在距被检站半径为150 km范围内且拔海高度相差在300 m以内的5个气象站。

根据文献[11]的原理，可通过计算日序为i的数据质控参数值来判断其质量状况，即

(3)

式 (3) 中，y_i和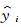分别为日气温观测值和估计值；σ为日气温估计误差的标准差，该标准差的统计时段为1个月 (为被检日期所在月)；f_i为质量控制参数 (简称质控参数)，其大小可表示观测值y_i的质量状况，显然|f_i|越大，y_i越可疑，甚至为错误数据。根据统计学原理，将质控参数值|f_i|≥3的数据标注为奇异值。上述基于线性回归数据估计方法来计算数据的质控参数值，以判断数据质量的检查算法，称为线性回归质量检查算法。

本文采用文献[10-11]的方法，即通过植入误差，来评价线性回归质量检查算法的错误数据检测性能。该方法是将实际观测数据人为加上一定幅度的数值 (即植入误差)，然后采用质量检查算法对含有植入误差的数据进行质量检查，以检验不同幅度植入误差的检测能力。为此在华中三省选取10个站 (其中湖南省、河南省各3个站，湖北省4个站)1961—2009年的逐日气温资料，分别加上一定幅度的植入误差 (1.2~3.0℃)，然后利用式 (3) 计算f_i，并统计|f_i|≥3所占比例 (表 1)。当植入误差取负值时，结果与表 1数据基本相同，故对其不作分析。

表 1

表 1 各种植入错误数据的质控参数值|fi|≥3所占比例 (线性回归法) Table 1 The percentage of seeded errors data for quality control parameter more than 3(using linear regression method) 植入误差/℃ 平均气温/% 最高气温/% 最低气温/% 0.0 0.4 0.5 0.4 1.2 53.8 18.1 15.6 1.4 69.6 28.1 25.1 1.6 82.2 41.8 39.1 1.8 89.4 53.7 50.8 2.0 93.8 65.0 63.1 2.2 96.4 74.6 73.0 2.4 97.9 81.6 80.1 2.6 98.8 87.2 85.6 2.8 99.2 91.2 90.1 3.0 99.5 94.3 92.4 注：植入误差为0.0℃时, 表示实际观测数据|fi|≥3的比例。

表 1 各种植入错误数据的质控参数值|fi|≥3所占比例 (线性回归法) Table 1 The percentage of seeded errors data for quality control parameter more than 3(using linear regression method)

由表 1可知，当植入误差幅度为3.0℃时，质控参数值为3的数据超过了92%，其中平均气温超过了99%。由此可见线性回归质量检查算法可检测日气温为3℃以上的植入误差。

文献[9]比较了反距离加权插值法和空间回归检验方法，认为后者比前者性能更好。为此本文仅就线性回归质量检查算法与单一空间回归检验方法进行比较。

空间回归检验方法在利用邻近站进行插值时，并不是按照反距离加权插值法将最大权重赋给最近的台站，权重大小依据被插值站与邻近站的均方根误差大小来选取，具体算法见文献[11, 16]。本文采用该方法进行数据估计时，从与被检站距离最近的8个站中挑选相关系数最大的5个站作为邻近参考站。

从统计结果来看 (数据表略)，虽然两种方法估计值的平均误差均很小，但单一空间回归检验方法的平均绝对误差和标准差远远大于线性回归检查算法，由此表明后者的数据估计精度明显高于前者。

由单一空间回归检验方法植入误差的检测情况 (表 2) 可看出，当植入误差的幅度为3.0℃时，最高气温和最低气温只有60%左右数据的质量控制参数值达到了3，明显低于线性回归质量检查算法的比例 (表 2数据的统计台站和资料日期与表 1相同)。

表 2

表 2 各种植入错误数据的质量控制参数值|fi|≥3所占比例 (空间回归法) Table 2 The percentage of seeded errors data for quality control parameter more than 3(using spatial regression test) 植入误差/℃ 平均气温/% 最高气温/% 最低气温/% 0.0 0.7 0.6 0.9 2.2 65.4 22.4 33.2 2.4 72.0 30.6 40.6 2.6 77.0 39.2 47.7 2.8 80.9 48.0 54.3 3.0 84.1 56.1 60.2 3.2 86.8 63.4 65.4 3.4 89.3 69.4 69.8 3.6 91.4 74.6 74.0 3.8 93.3 78.6 77.5 4.0 94.9 81.9 80.7 注：植入误差为0.0℃时, 表示实际观测数据|fi|≥3的比例。

表 2 各种植入错误数据的质量控制参数值|fi|≥3所占比例 (空间回归法) Table 2 The percentage of seeded errors data for quality control parameter more than 3(using spatial regression test)

通过对两种方法的绝对平均误差、标准差和植入误差的检测情况比较，线性回归质量检查算法的错误数据检测性能明显优于单一空间回归检验方法，产生该现象的原因可能与它们的方法有关。虽然两者均使用了回归方法，但单一空间回归检验方法只是利用回归方法来确定与邻近站权重，然后根据该权重计算被检站数据大小^[9-11]；而线性回归质量检查算法是通过式 (2) 直接计算被检站的估计值。从这方面来说，线性回归质量检查算法是一种集时间一致性和空间一致性检查于一体的质量检查方法，而空间回归检验方法基本上还是较为单一的空间一致性检查方法。

线性回归质量检查法包含了时间和空间一致性检查两种方法，为提高质量控制效果，在此基础上增加内部一致性检查，并将该方法称为综合一致性数据质量控制方法。所增加的内部一致性检查是基于气温 (日平均气温、最高气温、最低气温)、降水和日照时数等相关要素之间的变化规律来检查数据质量。因前文讨论的线性回归质量检查算法包含了时间和空间一致性方法，所以这里仅讨论新增的内部一致性检查方法。

利用日平均气温、最高气温、最低气温3个要素相关性，即内部一致性来进一步检测数据质量。如某站某日的最高气温质控参数值|f_i|≥3，表明其与周围站相比偏高。出现该现象有两种可能，一是该数据为奇异值，二是天气原因，即可能该站为晴天，而周围站为阴天或雨天。如为天气原因，一般来说日平均气温也偏高 (和邻近站比)，这样在检查最高气温时，同时参考日平均气温质控参数值，如同时偏高或偏低，一般认为是该站的天气和邻近站不一样造成，所检测的数据为有效值，即假设被检要素和参考要素同时为奇异值且同时偏大 (或偏小) 的可能性很小。该假设对于历史资料是合理可信的，因为历史资料中逐日最高、最低气温和平均气温是由不同温度表测量得到，且观测时间也不一样，所以它们同时产生错误的概率非常小。如发生被检要素与参考要素质控参数值同时明显偏高 (或偏低) 现象，可认为是被检站天气与邻近站的差异造成，被检数据为有效数据，否则为奇异值。

下面以一个实例说明气温相关性的一致性检查情况 (表 3)。湖北郧西站1992年5月6日最高气温质控参数值为5.83，而同日的平均气温质控参数值为4.51。如仅仅从最高气温质控参数值来判断，显然应被标注为奇异值，但如参考平均气温质控参数，则判定最高气温为有效数据。

表 3

表 3 1992年5月6日郧西站及其邻近站日气象要素 Table 3 The meteorological elements of Yunxi Station and its neighboring stations on 6 May 1992 气象要素 郧西 邻近参考站 竹溪 郧县 竹山 房县 老河口 平均气温/℃ 23.2 21.2 20.0 21.9 20.4 18.6 最高气温/℃ 27.5 24.6 22.0 24.8 23.8 22.9 最低气温/℃ 20.2 19.8 18.1 20.6 18.4 17.6 日照时数/h 2.3 0.0 0.0 0.0 0.0 0.0 降水量/mm 0.0 5.0 7.5 20.2 53.1 37.5

表 3 1992年5月6日郧西站及其邻近站日气象要素 Table 3 The meteorological elements of Yunxi Station and its neighboring stations on 6 May 1992

如某站有降水，而邻近站均无降水，或某站无降水，而邻近站均有降水发生，这两种情况也会可能导致日气温被错误标注为奇异值。本文通过计算两个次序量C_R，C_S来配合气温的内部一致性检查。其中C_R表示待检站待检日的降水量大于邻近站同日降水量的站次数，C_S表示待检站待检日的日照时数小于同日邻近站日照时数的站次数。这样可结合次序量C_R，C_S的大小实施降水量、日照时数等要素内部一致性检查。

基于线性回归质量检查算法，利用式 (3) 计算气温的逐日质控参数值f_i，依据表 4规则标注各要素的初始质控码F，质控码F的大小表示数据质量状况，其值越大，表明该数据为错误的可能性越大。

表 4

表 4 内部一致性质量控制方法标注规则 Table 4 The flagged rules of the internal consistency data check method 被检要素 质控参数 参考要素 质控参数 修正前 质控码 修正后 质控码 |fi|≥7 |fi|≥3 F=4 F=1 5≤|fi| < 7 2≤|fi| < 3 F=3 F=1 3≤|fi| < 5 1≤|fi| < 2 F=2 F=1 |fi| < 3 |fi| < 1 F=0 F=0

表 4 内部一致性质量控制方法标注规则 Table 4 The flagged rules of the internal consistency data check method

日最高气温、最低气温的参考要素为日平均气温，而日平均气温的参考要素为日最高气温、最低气温。对于日最高气温、最低气温，如同日的日平均气温质控参数值符号与其相同，则按照表 4中参考要素的规则修正质控码。如符号不相同，则质控码不变。

对于日平均气温，同日的日最高气温或最低气温中如果有一个要素质控参数值符号与其相同，则按照表 4中参考要素的规则执行 (如果2个均同号，则取绝对值最大者)，如符号均相反，则平均气温质控码不变。

对于最高气温、最低气温，当f_i < 0时，如C_R≥3或C_S≥3，则质控码F减1。平均气温不参考降水量和日照时数要素，即对其不进行内部一致性检查。

经过3.3.1 ~3.3.3节所描述步骤，最后的质控码即为该数据的质控码。本文将数据质量状况分为3级，即错误、可疑和正确。其中F≥3，表示该数据错误 (奇异值)，F=2表示数据可疑，F≤1表示数据正确。

在数理统计中定义了两种类型的错误，即如将正确数据标注成错误数据而拒绝，则称发生了第一类错误；如将错误数据标注成正确数据而接受，则称发生了第二类错误。在一般气象数据质量控制工作中，发生第一类错误的可能性较大。如仅采用线性回归质量检查算法，将最高气温|f_i|≥3的数据标记为奇异值，就有0.5%左右的数据被标注 (表 1)，这样在华中三省中就有两万多个日最高气温被标注，因该资料已经过基本质量检查，显然不可能包含如此多问题数据。当对部分标注的数据进行人工质量控制时，发现其中大部分数据并无质量问题，即第一类错误发生率较高。

在一般气象数据质量控制时，通常是按顺序提交各质量检查方法，最后综合各方法标注结果，决定数据的质控码。这样就失去了各方法的逻辑联系。如时间一致性检查某数据为奇异值 (可疑，偏高)，而空间一致性检查该数据也为奇异值 (可疑，但偏低)，则最后在综合确定其质量时，很有可能将其标注为错误数据 (因该数据有两个主要的质量检查方法没有通过)，但如将时间一致和空间一致性检查同时进行且参考奇异值偏离方向 (偏高或偏低，即方法之间的逻辑联系)，该数据就会被标注为有效数据。另外还存在一个问题，即目前许多数据质量控制方法很少考虑特殊天气和中小尺度天气对数据质量标注的影响。

综上所述，当前的一般数据质量控制方法存在3个方面的不足：第一类错误发生率较高；各种质量控制方法之间缺少逻辑性；大都基于气候原理和统计方法，很少考虑天气因素。

经统计，当最高气温质控参数值f_i≥3(或f_i≤-3) 时，该站同日参考要素平均气温的质控参数值f_i≥1(或f_i≤-1) 中的比例为52%(即有52%比例的日最高气温采用综合一致性质量控制方法中内部一致性检查后，可将标注为错误的数据降低为可疑数据乃至正确数据)；而日最低气温参考要素达到相同质控参数值的比例为68%，平均气温则为85%。由此可见，仅气温相关性的内部一致性检查一项至少可减少第一类错误发生率一半以上，其中平均气温减少更多。如加上降水量、日照时数参考要素的内部一致性检查，综合一致性质量控制方法第一类错误发生率还会下降更多。

一般数据质量控制方法的质量控制码是一次标注，而综合一致性控制方法在质量控制过程中，依据数据发生异常的逻辑关系，对质量控制码的大小进行增加或减少；同时综合一致性质量控制方法是将时间一致性、空间一致性和内部一致性3种检查作为一个整体进行检查，在检查过程中，充分考虑了质量控制参数值大小与符号，这样就完整保留了各种方法的逻辑关系，不会出现一种方法检查某个数据偏大，另外一种方法检测出该数据偏小，而最后综合决策时将该数据标注为奇异值的情况发生。

在气象数据质量控制工作中，常出现以下情况，即当发生一些中小尺度特殊天气现象时，导致很多无质量问题的数据被标注。Fiebrich等^[19]在对美国中尺度天气网的气象观测数据质量控制时，分析了特殊天气现象对数据质量标注的影响。本文在综合一致性质量控制方法中将降水量和日照时数作为日气温数据的参考要素进行内部一致性检查，某种程度上也是参考了部分特殊天气造成日气温空间分布不连续。

经统计，湖北省云梦站1985年12月22日最高气温的质控参数值为12.78，平均气温的质控参数值为0.42，可见云梦站该日最高气温与邻近参考站相比明显偏高，而日平均气温与邻近站相比差异不大 (从表 5中数据可知，云梦站该日最低气温与邻近站相比差异也不大)。所以从气象要素的内部一致性判断，该站该日最高气温可能为奇异值，且偏高。同时邻近站均无降水 (表明邻近站气温不可能因雨降温而使该站的气温较邻近站偏高)，由此表明，云梦站该日最高气温显著高于其他邻近台站的理由难以成立。

表 5

表 5 1985年12月22日云梦及邻近参考站气象要素 Table 5 The meteorological elements of Yunmeng Station and its neighboring stations on 22 Dec 1985 气象要素 云梦 邻近参考站 京山 安陆 应城 孝感 汉川 平均气温/℃ 0.8 0.6 0.2 0.9 1.3 1.9 最高气温/℃ 9.4 6.9 5.3 5.8 4.8 5.4 最低气温/℃ -1.8 -2.5 -1.4 -1.5 -1.4 -0.9 日照时数/h 0.0 1.6 0.0 1.2 0.0 0.0 降水量/mm 0.0 0.0 0.0 0.0 0.0 0.0

表 5 1985年12月22日云梦及邻近参考站气象要素 Table 5 The meteorological elements of Yunmeng Station and its neighboring stations on 22 Dec 1985

另外，从云梦站与邻近站该日前后的最高气温时间变化 (图 1) 来看，云梦站除该日明显偏高外，其他日期与其他站变化趋势相同。云梦站该日4个时次 (02：00，08：00，14：00，20：00，均为北京时，下同) 的正点气温分别为-0.2，-1.5，4.2，0.6℃，而该日日照时数为0，所以日最高气温从14：00的4.2℃上升到9.4℃可能性较小。

图 1

图 1. 1985年12月15—31日云梦及邻近站最高气温随时间变化 Fig 1. The daily maximum temperature of Yunmeng Station and its neighboring stations during 15—31 Dec 1985

综合上面的分析可知，云梦站该日最高气温9.4℃为奇异值 (其质控码F=4)。该奇异值的产生很有可能是气温人工观测过程中较易出现的5℃误读现象造成，即云梦站该日最高气温实际值可能为4.4℃。

通过应用综合一致性质量控制方法的检查，华中三省日气温数据的奇异值检出率平均气温为0.001%，最高气温为0.05%，最低气温为0.04%。经对奇异值分布分析发现，在标注为奇异值的数据中，最高气温的质控参数值为正的数据个数远远多于质控参数值为负的数量，而最低气温正好相反，即最高气温奇异值一般高于实际值，最低气温的奇异值一般低于实际值。分析表明，产生该现象的原因在于本文使用的数据前期经过基本质量控制，并修正了其中的错误数据。如最高气温发生与实际观测数据偏小的错误，将可能导致与逐小时的正点观测气温矛盾，从而前期在质量检查时，就会无法通过内部一致性检查，因此该错误数据得到了更正。但当最高气温发生偏高的错误 (或最低气温发生偏低错误) 时，内部一致性检查缺乏错误检测能力，故这些错误仍然被保留着。所以通过奇异值的分布特点可看出，综合一致性质量控制方法的确能检测出许多隐藏在数据集中的奇异值，从另一方面说明了该方法具有更好的错误数据检测性能。

本文主要任务是通过研制数据质量控制方法为华中区域气象中心研制一套高质量的日气温数据集，为区域气候变化评估报告提供数据支持。为此本文设计了基于线性回归数据估计方法的质量检查算法，并在该算法的基础上，研制了综合一致性数据质量控制方法，对1961—2009年华中区域三省251个站历史日气温资料进行了质量检查，取得了较好的应用效果：

1) 通过分析比较可知，基于线性回归数据估计方法的质量检查算法的错误数据检测性能较高，可检测出日气温与正确数据相差3℃左右的可疑数据。

2) 综合一致性数据质量控制方法参考了天气因素，并在质量控制过程中保持了时间一致性、内部一致性和空间一致性的逻辑关系，与一般的数据质量控制方法相比，具有较高的错误数据检测性能。

本文在综合一致性数据质量控制方法中，尽管参考了中小尺度天气对数据奇异值标注影响，但天气因素对数据质量标注影响还需更深入研究，这也是今后工作的方向。此外，由于在自动气象站中，日平均气温、最高气温、最低气温均为同一传感器的测量值，故综合一致性数据质量控制方法的气温相关性检查的检测效率会受到一定影响，可选择地温作为替代参考要素。