2. 天津市气象台,天津 300074;
3. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. Tianjin Meteorological Observatory, Tianjin 300074;
3. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
多普勒天气雷达作为探测降水系统的主要工具,不仅能实时估测雷达扫描范围内各点的雨强和一定区域上的降水量分布,而且可以及时获取大面积定量的降水资料,这对工农业生产、天气预报、云雾降水物理研究、人工影响局部天气的效果检验、水文学上估算江河流量及在汛期及时发布洪水警报等方面都有一定意义[1]。但雷达估测降水效果易受多种因素影响,如地物杂波和超折射回波及零度层亮带等,还有雨滴谱变化造成的影响,另外雷达估测降水的效果与降水类型、地面降水差异等也有关,这均会造成雷达降水估测值和实测值之间存在较大差异[2]。为此,人们研究了各种方法来消除或者减小这些因素对雷达估测降水的影响。
在对如何消除地物杂波和超折射回波等对雷达估测降水的影响方面,前人做了大量研究工作[3-5],提出许多有效的自动处理雷达原始资料的方法,例如检查反射率回波的时空连续性[6],分析反射率的水平梯度和垂直梯度[7],以及采用模糊逻辑算法的雷达回波分类技术[8]等多种方法。美国大气研究中心 (NCAR) 已将综合使用反射率因子、径向速度和速度谱宽识别地物回波和超折射回波的模糊逻辑法广泛应用于WSR-88D天气雷达ORPG (Open Radar Product Generator) 系统中。在国内,刘黎平等[9-10]也开展了基于模糊逻辑的分布式超折射地物回波识别方法的研究。
而对于如何减小雷达估测降水量与地面实测值之间的差异、提高雷达估测降水的精度,采用的最基本的方法是基于雨量计校准,即采用客观分析方法,包括最优插值方法[11]、Kriging法[12]、Kalman滤波[13-15]、变分校准方法[16]、概率配对法[17]等,在空间上提取校准场,从而得到校准后的降水分析场,还有利用反射率因子垂直廓线联合雨量计校准区域降水[18]以及联合卫星定量监测预报降水[19]等。但基于雨量计校准的前提是要求地面要有一定密度分布的雨量计站网,以保证有质量好的校准因子值。1970年Wilson[20]就证实1部雨量计可以改善雷达在2590 m2区域内对降水量的测量,使其均方根误差减小39%。Brandes[21]则研究了基于雨量计单点校准的雷达估测降水的空间变化。Harrold等[22]分析了与雨量计相对应的不同区域范围雷达测量的误差特征,用以研究在相对近距离范围内校准雷达估测降水所需要的雨量计密度。而Collier等[23]从布设在1000 km2的62部雨量计中选择了55部,用逐步减少校准雨量计个数的方式进行不同密度雨量计校准雷达的研究。Woodley等[24]对美国南部不同流域面积内发生对流性降水时的雨量计密度进行了研究分析,指出在570 km2的加密试验区域内需要的校准雨量计密度为1部/26 km2;当研究区域扩大至13000 km2时,所需雨量计密度为1部/143 km2。而Young等[25]研究指出在小尺度范围内建立高密度雨量计站网对于确定降水的相关结构非常重要。但在国内相关的研究还很少,而且研究重点是在结合水文模式开展的联合雨量计校准雷达对流域降水量和水文影响的模拟研究上[26-27]。本文在对比质量控制前后雷达估测降水量和雨量计降水量相关性的基础上,采用雷达-雨量计联合校准方法,分析不同密度雨量计校准对雷达估测降水效果的影响、不同校准方法的校准差异及各自的校准优势,以期为开展联合雨量计校准雷达估测降水业务的实施及地面自动气象站的合理布设提供参考依据。
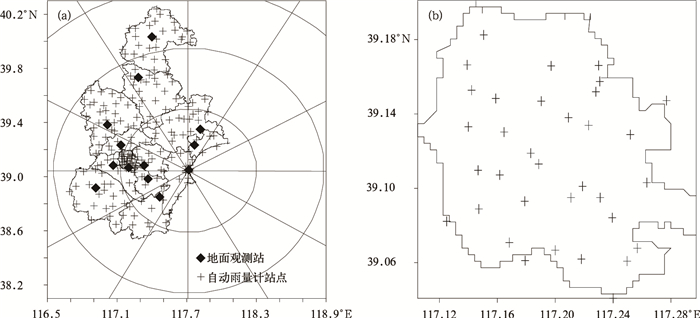
1 雷达与加密自动站网分布及资料选取 1.1 雷达和加密自动站网分布天津位于华北平原东北部,渤海西岸,区域内设有13个地面观测站 (人工观测与自动站同步进行观测) 和219个自动雨量计站点,雷达位于天津的滨海新区 (图 1)。从图 1看到,天津232个雨量计站点均在雷达140 km探测范围内,而且约80%的站点分布在20~100 km之间 (图略),这样在分析不同密度雨量计站网校准对雷达估测降水效果的影响时,雷达探测距离对其影响可以忽略不计。
|
|
| 图 1. 天津地面观测站、自动雨量计站点 (相邻距离圈间隔为50 km)(a) 及天津市区自动雨量计站点 (b) 分布 Fig 1. Distributions of Tianjin weather stations and rain gauges (the interval between adjacent circles is 50 km)(a) with Tianjin urban rain gauges (b) | |
1.2 资料的选取与匹配处理
雷达资料采用天津多普勒天气雷达基数据资料,降水量资料为天津地面观测站人工观测降水量资料和加密自动雨量计资料,选取的天气个例共11个,分别为2008年6月25日与6月27日积云强降水过程、2009年7月22日10:00—15:00(世界时,下同) 及19:00—23:00两个时段的积云强降水过程,2008年7月4日、7月14日和2009年6月8日、6月18日和7月17日积云层云混合性降水过程,2008年9月9日和2009年4月18日、4月19日层云稳定性降水过程。
由于雷达是以极坐标方式扫描,雷达低层探测资料易受到地物杂波和超折射回波等非气象回波的影响,所以在对比分析雷达估测降水量和雨量计降水量之间的相关性时,雷达资料选用0.5°仰角PPI资料,以雨量计站点位置为准,采用最自然临近方法,选取和雨量计站点位置相对应的雷达回波强度值,采用雷达默认Z-I关系 (Z=300I1.4) 将回波强度值转换成降水强度,再通过累积分别得到6 min和1 h时间尺度的雷达估测降水量资料。考虑到雷达探测与地面自动站观测方式不同及降水的时空变化等可能造成的观测误差,6 min和1 h时间尺度的降水量资料均以当前时刻雷达估测降水量和下一时刻雨量计降水量相对应。
2 雷达资料和雨量计资料的相关分析雷达资料和自动站资料质量是影响降水估测的重要原因,为此在开始校准雷达估测降水分析前,本文首先分析雷达和雨量计资料的质量。
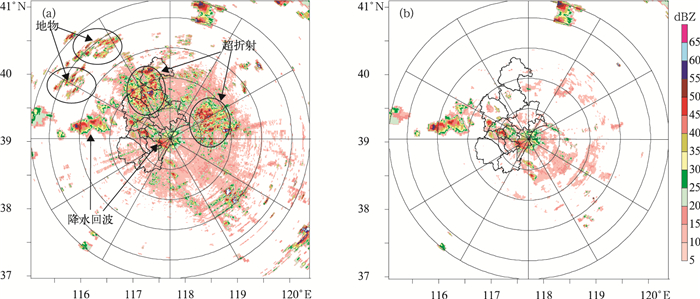
2.1 雷达资料和雨量计资料的质量分析 2.1.1 雷达探测资料的质量分析与控制采用中国气象科学研究院灾害天气国家重点实验室开发的雷达基数据资料杂波抑制程序[9-10], 对雷达资料进行质量控制。通过对多次受地物和超折射回波污染降水过程的雷达资料进行质量控制,效果均较好。图 2为2005年7月30日07:37 0.5°仰角雷达PPI图,对比质量控制前后PPI图可以看到,对雷达资料进行质量控制后,地物和超折射回波被有效去除,降水回波清晰可见。由于影响雷达资料质量的因素很多,本文仅就由地物和超折射回波对雷达资料质量造成的影响进行质量控制,其他因素对雷达资料质量的影响及处理方法没有涉及。
|
|
| 图 2. 2005年7月30日07:37天津雷达0.5°仰角PPI图 (a) 质量控制前,(b) 质量控制后 Fig 2. 0.5° elevation angle Tianjin radar PPI at 0737 UTC 30 July 2005 (a) before quality control, (b) after quality control | |
2.1.2 雨量计资料的质量分析与控制
对自动雨量计设在地面观测站内、有人值守并同步进行人工观测的13个自动雨量计降水量资料,应用2005—2007年降水量资料,以人工观测日降水量不低于0.1 mm为有效数据,选取自动和人工观测在时间上完全对应的资料,以人工观测降水量值为真值,分别计算雨量计测量的绝对误差、相对误差、测量偏差 (真值/测量值)、相关系数及误差较大站 (次) 所占的比例。从计算结果和二者的对比可知 (图略),雨量计测量值略高于人工观测值;日平均绝对误差和相对误差很小, 分别为0.17 mm和1.9%,相关系数达到0.996;只有0.5%站 (次) 的降水量资料误差较大。分析误差较大降水过程出现误差的原因,主要为自动站仪器故障或外界因素影响,另外测量时间不同步也可造成两种观测的日降水量误差较大。
对于无人值守自动雨量计资料,以雷达观测为依据,将雨量计资料与雷达降水回波进行对比,对雷达低层 (0.5°和1.5°仰角) 探测有回波而雨量计监测无降水、或雨量计有明显降水而相应位置上雷达探测没有降水回波的雨量计资料均作为无效资料处理。对2008—2009年多次降水过程的雨量计资料进行质量分析统计看到,对于小时降水量资料,每次过程平均有217个雨量计的资料可用,占93.5%;对于分钟降水量资料而言,每次过程平均只有152个雨量计的资料有效。而仪器故障及人为因素等是造成雨量计资料不可用的主要原因,由于造成雨量计资料误差较大的原因也很多且复杂,本文只就因仪器故障原因造成误差较大的雨量计资料进行了分析和剔除。
2.2 雷达估测降水量和雨量计降水量的相关性分析 2.2.1 统计指标采用比率、均方根误差和相关系数作为相关分析统计指标 (计算公式略)。根据定义,比率大于和小于1.0,分别表示雷达估测降水量相对真值的偏低估计和偏高估计; 均方根误差表示雷达估测降水量相对于真值的离散程度,值越小表明离散程度越小; 相关系数越接近1.0,表示雷达估测降水量值同真值的相关性越高。
从11个个例中选取降水时间较长的6次降水过程、共取得42 h的降水量资料,通过对雨量计资料和雷达资料分别进行质量控制分析可知,质量控制前9744对1 h时间尺度和97440对6 min时间尺度的降水量数据,质量控制后得到6384对1 h时间尺度和63840对6 min时间尺度的有效降水量数据。
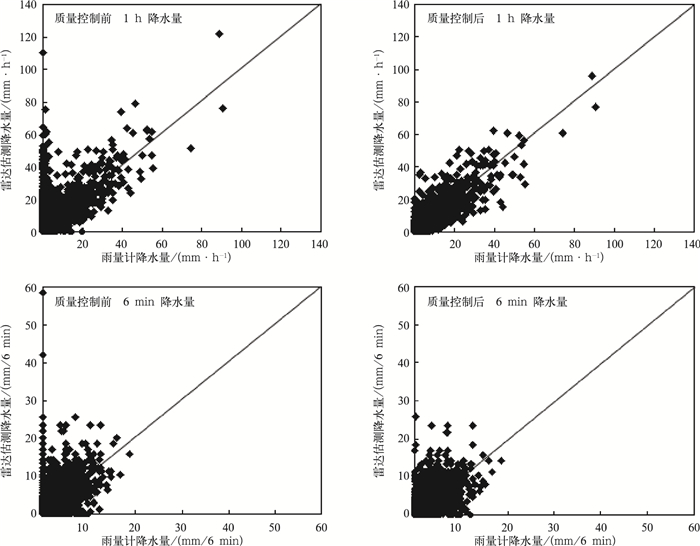
2.2.2 相关性分析通过计算对比分析看到,质量控制前,6次过程的平均比率为0.679,6 min和1 h两种时间尺度的雷达估测降水量均出现偏高估计,平均高估32.1%,单次过程偏高估计最大超过50%;雷达估测降水量和雨量计降水量之间的相关性也不高,平均仅为0.45左右,而单次降水过程1 h的相关系数最小仅为0.095。质量控制后,6次过程的平均比率由不足0.7提高到了1.142,雷达估测降水的高估情况得到明显改善,由质量控制前的估测偏高调整为相对于雨量计降水量真值的估测略低;二者的相关性也明显加大,1 h降水量的平均相关系数提高幅度在0.3以上, 达到0.826,略高于6 min时间尺度的;而且单次降水过程1 h的相关系数提高幅度最大达到0.7。而且质量控制后两种时间尺度的均方根误差均明显小于质量控制前的。图 3为质量控制前、后两种时间尺度雷达估测降水量和雨量计降水量的对比散点图。从图 3可以看到,质量控制前,落在两个坐标轴上的点非常多,就是说雷达探测有降水回波而自动站降水量为零和雷达探测无降水回波 (估测降水量值为零) 而地面有降水的数据很多。质量控制后,这些点多数被剔除,雷达对降水估测明显偏高的现象也有较好改善,雷达对部分站点降水量的估测由质量控制前的偏高调整为相对自动站真值的略偏低,雷达估测降水量和雨量计降水量的相关性有了明显提高。
|
|
| 图 3. 雷达估测降水量与雨量计降水量的对比散点图 Fig 3. Scatterplot of radar rainfall estimation and rain gauge rainfall | |
分析雷达估测降水量和自动站降水量相关性差的数据 (图 3中落在两个坐标轴上的点) 出现的原因,落在x轴上的点主要是因自动站仪器故障等造成的虚假降水量值;或因降水回波离雷达太近雷达没有观测到 (雷达扫描静锥区内的降水回波),这是由雷达扫描方式造成的。落在y轴上的点主要是因自动站仪器故障导致降水量值失真 (值为零) 或由地物杂波和超折射回波等对雷达探测污染造成的。对于这些点在分别对雷达探测资料和雨量计资料进行相应的质量控制后,基本可以去除。但由于雷达探测和自动雨量计测量空间取样的不一致,雨滴谱的时空变化又很大[28],所以造成二者相关性差的原因很多,本文仅就二者质量问题造成其相关性差点出现的原因进行分析。
3 雨量计密度对校准雷达估测降水效果的影响联合雨量计校准雷达,可以充分利用雨量计单点测量准确的优点,同时又保留雷达对降水定量估测的分布特征。
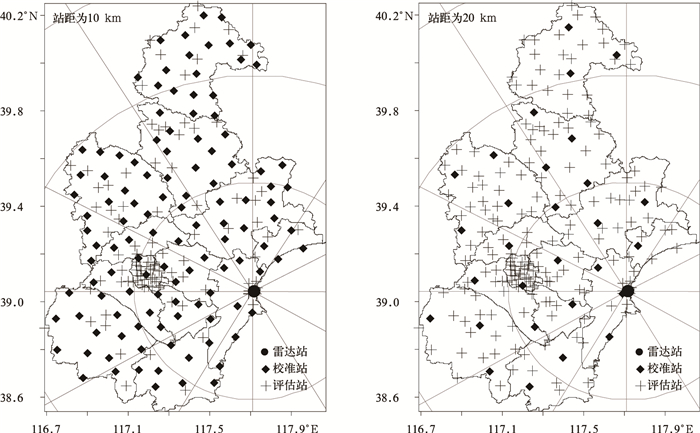
3.1 校准雨量计密度选取及校准方案根据天津自动站网分布特点 (图 1),将雨量计分为两部分:一部分作为校准站点进行校准试验,另一部分作为评估站点以检验校准结果。以232个自动雨量计为准计算,天津地区雨量计密度约为19.7×10-3·km-2。因天津市区的雨量计密度远大于其他区县,所以在选取上先以天津市所有雨量计平均站距作为最大密度雨量计站距进行选取,然后与其他地区同步,通过不断减小雨量计站点间距离,达到逐步加大校准雨量计站点密度的目的。剩余所有雨量计站点均作为检验评估站。根据上面分析结果知,每次天气过程平均有15个自动雨量计的资料无效,在选取校准站点时以此为依据,共选定14种不同密度分布的雨量计网参加校准 (表 1)。图 4为其中两种雨量计网的站点分布图。考虑到自动站实际分布的不均匀性,文中所列雨量计站距为近似值。
|
|
表 1 不同校准密度的雨量计站点分布方案 Table 1 Different density of rain gauge calibration program distribtution |
|
|
| 图 4. 校准雷达的雨量计站点密度分布示意图 (相邻距离圈间隔为50 km) Fig 4. Rain gauge site density distribution schematic for calibrated radar (the interval between adjacent circles is 50 km) | |
校准方法采用黄淮项目雷达估测降水算法软件中的变分校准技术方法、卡尔曼滤波校准法和最优插值校准法3种方法,其校准原理参见文献[1, 29]。校准时采用雷达默认Z-I关系 (Z=300×I1.4),校准的时间步长为1 h。以雨量计降水量作为真值,分析比较比率、均方根误差、相关系数3个指标的变化。
3.2 雨量计校准雷达估测降水结果分析 3.2.1 不同雨量计密度校准对雷达估测降水精度的影响通过对所选11个个例的校准结果进行分析可知,当参加校准的雨量计密度较小时,校准雷达估测降水的误差较大,统计指标值很不稳定。随着校准雷达雨量计密度的逐渐加大,雷达估测降水的效果明显好转,估测精度不断提高并在某一校准雨量计密度后趋于稳定。而且从校准后雷达估测降水出现的最大过高估计和最小过低估计值可知 (表略),随校准雨量计密度的加大,雷达对降水高估和低估的极值不断减小。
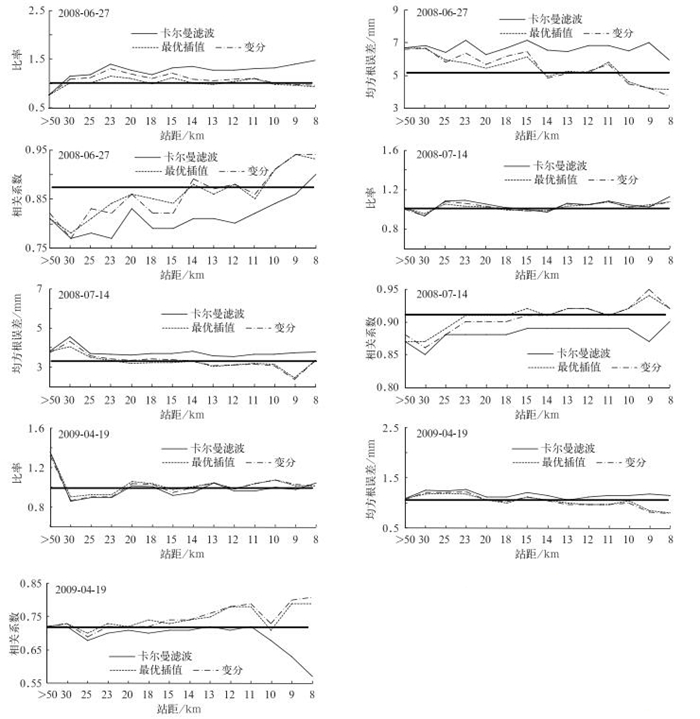
对积云强降水过程,当校准的雨量计密度较小时,雷达对降水的估测明显偏低,均方根误差较大,相关系数较小。对于2008年6月27日降水过程,当站距为23 km的雨量计密度校准雷达时,雷达对降水明显低估约20%,且估测值相对真值的离散度较大,校准雷达的效果不理想。而随着校准雨量计密度的加大,比率渐渐趋向1, 均方根误差逐渐减小,相关系数不断加大。当雨量计站距为14 km时,比率接近1(卡尔曼滤波方法的值略低,3种校准方法的校准差别在后面讨论), 均方根误差达最小 (小于5 mm), 相关系数也达到0.88以上 (图 5)。对于2009年7月22—23日及2008年6月25日积云强降水过程,当雨量计站距为13 km时,雷达估测降水的结果和真值接近 (图略),之后即使增加校准雨量计的密度,3个指标也未出现明显改善。雨量计站距为13~14 km时对应的雨量计密度平均为5.6×10-3·km-2。这表明当雨量计布设密度为5.6×10-3·km-2时,雷达估测降水的结果和真值比较接近,之后再增加校准的雨量计密度,雷达估测降水的精度无明显进一步提高,此时天津范围平均每182 km2需布设1部雨量计。
|
|
| 图 5. 2008年6月27日、2008年7月14日、2009年4月19日3次降水过程统计指标随校准雨量计密度的变化 (>50 km表示全区只有1部雨量计参加校准) Fig 5. Performance measures for rain gauge calibration density on 27 June 2008, 14 July 2008 and 19 April 2009 ( > 50 km denotes only one rain gauge calibration) | |
对积层云混合性对流降水过程,当校准的雨量计密度较小时,雷达估测降水的偏差很大,估测效果不稳定;随着校准雨量计密度的加大,雷达估测降水的精度得到提高并逐渐趋于稳定。对于2008年7月14日过程,当雨量计站距为15 km时,比率趋近于1,均方根误差达到最小,为3.5 mm,相关系数平均达到0.9以上 (图 5);而对于2009年7月17日积云层云混合性降水过程,当雨量计站距为14 km时,3个指标达到最优:比率约为1,均方根误差小于1.5 mm,相关系数达到0.9左右 (图略)。对于这种类型的5次降水过程,随校准雨量计密度的不断加大,雷达估测降水的效果均得到改善,并在站距为14~15 km时雷达估测降水的精度有明显提高并趋于稳定。站距为14~15 km时的雨量计密度为4.8×10-3·km-2,这表明当雨量计布设密度大于4.8×10-3·km-2以后,校准雷达估测降水的精度无明显进一步提高,此时天津范围平均每211 km2需布设1部雨量计。
对于2009年4月19日等3次层云稳定性降水过程,通过同样的分析知 (图 5),当雨量计站距不大于20 km、即当雨量计密度不小于2.5×10-3·km-2以后,校准雷达估测降水的精度无明显提高,此时天津范围每405 km2需布设1部雨量计。
因此,用不同密度雨量计校准雷达估测不同类型降水过程,校准效果及需要的雨量计密度与降水类型有关,对于积云强降水来说,需要的校准雨量计密度要大一些;对于积云层云混合性降水来说,所需的校准雨量计密度略低;而层云稳定性降水需要的校准雨量计密度相对最小。雷达估测降水量相对真值的离散程度也与降水类型有关,降水时空分布越不均匀,其离散程度越大,而且联合雨量计校准雷达对积云或积混降水的估测效果要好于对层云稳定性降水 (图 5)。
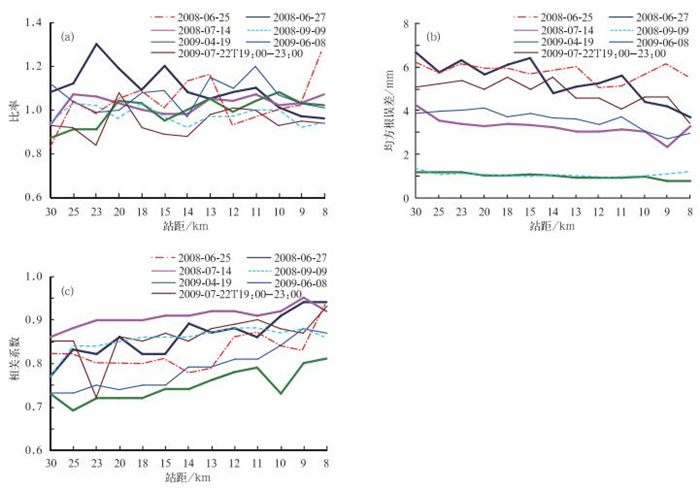
3.3.2 不同校准方法校准效果对比分析分析变分校准法的校准结果可知 (图 6),随着校准雨量计密度的加大,雷达估测降水精度不断提高,表现在比率逐渐趋近于1、均方根误差逐渐减小、而相关系数不断加大。而且校准积混对流性降水的估测偏差基本在6%以内、明显低于校准积云强降水的、略高于校准层云稳定性降水的;相关系数平均在0.8以上且随着校准雨量计密度的加大而迅速提高到0.85以上、略高于校准积云强降水的、但明显高于校准层云稳定性降水的;校准积混对流性降水的均方根误差值处于校准积云强降水的和校准层云稳定性降水的中间。对于最优插值法的校准效果 (图略),其校准效果与变分校准法基本相当,只是在校准的雨量计站网密度较小时,其校准效果略差一些。
|
|
| 图 6. 变分校准法的校准效果 Fig 6. The effects of variational calibration method | |
对于卡尔曼滤波法的校准效果,在校准的雨量计站网密度较小时,其校准效果和变分校准法及最优插值法的效果大体相当,但随着校准雨量计站网密度的不断加大,其校准效果明显差一些。对层云稳定性降水的校准,虽然和另两种校准法的比率基本相同,但随着校准雨量计站网密度的加大,相关系数明显偏小,最大差0.1以上,均方根误差偏大0.2以上;对积云强降水及积混对流性降水的校准效果,和另两种校准法相比,在相关系数偏小的同时,均方根误差及比率均明显偏大 (图略)。
分析3种校准方法校准效果出现差异的原因,应与其各自的校准原理有关。对于变分校准法,从校准开始就将同时有雷达回波和雨量计站点上的实测校准因子内插到各网格点上得到各网格点的校准因子,然后通过对其进行拟合而获得一个最优的校准因子分析场。所以使用不同密度雨量计站网校准雷达估测降水时,变分校准法的优点明显[1]。对于卡尔曼滤波校准方法,其属于线性无偏最小方差递推滤波,滤波效果的好坏取决于如何针对实况建立滤波方程。从其具体求解过程看,在任意给出初始值后,通过反复递推计算求得不同时刻的偏差校准量和误差方差,只有不断增加实际观测次数,其估计精度才能得到提高[1]。而最优插值校准是一种用统计方法在均方根误差最小意义下的最优线性插值。依照其基本原理,以回波为初值场,在有站点的地方对真值场进行取样,以此作为雨量计测得的降水量,用其对初值场订正,得到最优订正后的场,所以相对一般的加权方案,其校准优势明显[29]。
4 结论与讨论本文在对比分析质量控制前后雷达探测资料和自动雨量计资料相关性的基础上,选取14种不同密度分布雨量计对雷达进行校准,分析雨量计密度对雷达估测降水效果的影响,得到以下初步结论:
1) 天津自动雨量计资料质量基本可靠,仅有0.5%站次的降水量资料误差较大。对降水过程而言,平均每次有93.5%的雨量计小时降水量资料可用,而仪器故障或外界因素等是造成其误差较大的主要原因。
2) 对雷达资料进行去除地物和超折射回波的质量控制,能有效去除这些非气象杂波对雷达资料的污染,同时保留降水回波;而且雷达对降水的高估现象能得到明显改善,雷达估测降水量和自动雨量计之间的相关性也明显加大。
3) 联合雨量计校准雷达能明显提高雷达对降水的估测能力。随着校准雨量计密度的不断加大,雷达估测降水的精度不断提高并趋于稳定;应用雨量计校准雷达对积云强降水或积混对流性降水的估测效果要好于对层云稳定性降水。
4) 校准效果相同时,校准不同类型降水过程需要的雨量计密度不同;不同校准方法的校准效果也不同,变分校准法和最优插值校准法适合在雨量计密度高的地区校准雷达;卡尔曼滤波校准法适合在雨量计密度低的地区校准雷达。
由于影响雷达资料和自动站降水量资料质量的因素很多且复杂,本文对雷达资料和自动雨量计资料的质量控制与相关性分析还不全面,外界环境因素 (如风场) 等对资料质量的影响文中没有涉及,也没有就雨量计密度校准局地强降水及特殊点对校准雷达估测降水效果的影响等进行分析,仍需大量工作进行完善。
| [1] | 张培昌, 杜秉玉, 戴铁丕. 雷达气象学. 北京: 气象出版社, 2001. |
| [2] | Collier C G. Applications of Weather Radar Systems: A Guide to Uses of Radar Data in Meteorology and Hydrology. Chichester: Ellis Horwood Limited, 1989: 33–34. |
| [3] | Joss J, Wessels H. Ground Clutter Suppression for Weather Radar Data. Tech Rep COST Tech, Rep 73/WD/130, Note 1297, 1990. |
| [4] | Keeler R J, Passarelli R E. Signal Processing for Atmospheric Radars//Radar in Meteorology. Amer Meteor Soc, 1990: 199-230. |
| [5] | Pratte J F, Keeler R J, Gagnon R, ed al. Clutter Processing During Anomalous Propagation Conditions//Preprints, 27th Conf on Radar Meteorology. Amer Meteor Soc, 1995: 139-141. |
| [6] | Smith P L.Precipitation Measurement and Hydrology: Panel Report//Radar in Meteorology. Amer Meteor Soc, 1990: 607-618. |
| [7] | Collier C G, Lovejoy S, Austin G L. Analysis of bright bands from 3D radar data//Preprints, 19th Conf on Radar Meteorology. Amer Meteor Soc, 1980: 44-47. |
| [8] | Kessinger C, Ellis S, Van Andel J. NEXRAD Data Quality Enhancements: The AP Clutter mitigation Scheme//Preprints, 30th International Conference on Radar Meteorology, Amer Meteor Soc, 2001: 707-709. |
| [9] | 刘黎平, 吴林林, 杨引明. 基于模糊逻辑的分布式超折射地物回波识别方法的建立和效果分析. 气象学报, 2007, 65, (2): 253–260. |
| [10] | 刘黎平, 王致君. 双线偏振雷达探测的云和地物回波的特征及其识别方法. 高原气象, 1996, 15, (3): 303–310. |
| [11] | Daley R. Atmospheric Data Analysis//Cambridge Atmospheric and Space Science Series. Cambridge: Cambridge University Press, 1991. |
| [12] | Seo D J. Real-time estimation of rainfall fields using radar rainfall and rain gage data. J Hydro, 1998, 208: 37–52. DOI:10.1016/S0022-1694(98)00141-3 |
| [13] | Dinku T, Anagnostou E, Borga M. Improving radarbased estimation of rainfall over complex terrain. J Appl Meteor, 2002, 41: 1163–1178. DOI:10.1175/1520-0450(2002)041<1163:IRBEOR>2.0.CO;2 |
| [14] | Ninomiya K, Akeyama T. Objective analysis of heavy rainfalls based on radar and gauge measurement. J Meteor Soc Japan, 1978, 50: 206–210. |
| [15] | 尹忠海, 张沛源. 利用卡尔曼滤波校准方法估算区域降水量. 应用气象学报, 2005, 16, (2): 213–219. |
| [16] | 邓雪娇, 黄浩辉, 吴兑. 变分法在校准雷达定量估测降水中的应用. 应用气象学报, 2000, 11, (2): 255–256. |
| [17] | Rosenfeld D, Wolff D B, Amitai E. The windows probability matching method for rainfall measurements with radar. J Appl Meteor, 1994, 33: 682–693. DOI:10.1175/1520-0450(1994)033<0682:TWPMMF>2.0.CO;2 |
| [18] | 史锐, 程明虎, 崔哲虎, 等. 用反射率因子垂直廓线联合雨量计校准估测夏季区域强降水. 应用气象学报, 2005, 16, (6): 737–744. |
| [19] | 万玉发, 张家国, 杨洪平, 等. 联合雷达网和卫星定量测量与预报长江流域大范围降水. 应用气象学报, 1998, 9, (1): 94–103. |
| [20] | Wilson J W. Integration of radar and rain gage data for improved rainfall measurement. J Appl Meteor, 1970, 9: 489–498. DOI:10.1175/1520-0450(1970)009<0489:IORARD>2.0.CO;2 |
| [21] | Brandes E. Optimizing rainfall estimates with the aid of radar. J Appl Meteor, 1975, 14, (7): 1339–1345. DOI:10.1175/1520-0450(1975)014<1339:OREWTA>2.0.CO;2 |
| [22] | Harrold T W, English E J, Nicholass C A. The accuracy of radar-derived rainfall measurements in hilly terrain. Quart J Roy Met Soc, 1974, 100: 331–350. DOI:10.1002/(ISSN)1477-870X |
| [23] | Collier C G, Harrold T W, Nicholass C A. A Comparison of a Real Rainfall as Measured by a Rain Gauge Calibrated Radar System and Rain Gauge Networks of Various Densities//Preprints, 16th Radar Met Conf. Amer Meteor Soc, 1975: 467-472. |
| [24] | Woodley W L, Olsen A R, Herndon A, et al. Comparison of gages and radar methods of convective rain measurement. J Appl Meteor, 1975, 14: 909–928. DOI:10.1175/1520-0450(1975)014<0909:COGARM>2.0.CO;2 |
| [25] | Young C B, Bradley A A, Krajewski W F, et al. Evaluating NEXRAD multisensor precipitation estimates for operational hydrologic forecasting. J Hydro, 2000, 1: 241–254. DOI:10.1175/1525-7541(2000)001<0241:ENMPEF>2.0.CO;2 |
| [26] | 刘晓阳, 毛节泰, 李纪人, 等. 雷达估测降水模拟史灌河流域径流. 北京大学学报:自然科学版, 2002, 38, (3): 342–349. |
| [27] | 张亚萍, 程明虎, 徐慧, 等. 雷达定量测量降水在佛子岭流域径流模拟中的应用. 应用气象学报, 2007, 18, (3): 295–305. |
| [28] | Joss J, Gori E G. Shapes of raindrop size distributions. J Appl Meteor, 1978, 17: 1054–1061. DOI:10.1175/1520-0450(1978)017<1054:SORSD>2.0.CO;2 |
| [29] | 李建通, 杨维生, 郭林, 等. 提高最优插值法测量区域降水量精度的探讨. 大气科学, 2000, 24, (2): 263–270. |
 2012, 23 (1): 30-39
2012, 23 (1): 30-39



