2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
风廓线雷达是以大气为探测对象,应用大气湍流对电磁波散射原理进行大气探测的一种遥感设备[1],能对大气垂直风场结构进行实时、连续观测,也能对大气中降水云体的垂直结构进行探测,在对高空风场结构、锋面、低空急流活动以及降水、云体结构及大气折射率结构常数的探测和研究中得到了广泛应用[2-7]。风廓线雷达探测大气的能力与雷达采用信号处理与信息提取方法密切相关。风廓线雷达接收到的信号不可避免地混有雷达系统噪声,大气返回信号常低于噪声电平-40~-30 dB,设计合理的信号处理和提取方法是提高风廓线雷达探测高度与探测精度的关键。风廓线雷达的信号处理中广泛使用了相干累积技术和谱分析技术,但在实施中常因对信号的噪声处理、谱参数提取的具体实施方案不同,导致雷达对大气返回信号的提取能力和估测精度的差异,因此如何对信号处理和信息提取的结果进行检验,如何设计最优的信号处理方案是风廓线雷达信号处理中的关键技术。雷达返回信号的仿真模拟是对雷达提取信息能力进行检测评估的一种重要方法,已经在军事部门得到广泛的应用,除了对飞机、军舰仿真信号模拟外,对云雨杂波、地物杂波也进行了研究[8-12]。有关天气雷达的仿真模拟主要是对多普勒天气雷达的PPP,FFT处理方法进行对比研究[13],风廓线雷达返回信号的模拟研究的相关工作开展较少,很多工作是设备研制方基于噪声和大气返回信号的理论分布模型对谱分布进行仿真模拟,很少有基于雷达谱参数计算输出对谱分布的仿真模拟。同时由于风廓线雷达谱参数计算结果是设备研制方对谱信号分布经过相关算法提交,不同厂家的谱参数识别处理方法不同会导致谱参数输出结果的差异,针对以上情况本文在风廓线雷达回波信号强度定标[14]基础上对实测大气返回信号及雷达系统噪声谱密度分布统计分析的基础上,形成风廓线雷达谱数据仿真生成方法,对探测大气谱信号进行了仿真数据模拟,在此基础上建立了风廓线雷达大气返回信号谱仿真数据生成软件系统,应用不同谱参数生成的仿真数据对风廓线雷达的信号处理算法和谱参数计算结果进行了检验,并对谱参数计算精度进行了分析,以此对风廓线雷达探测的数据准确性进行评估。
1 风廓线雷达信号的谱分布特征风廓线雷达主要对晴空大气进行探测,接收的返回信号中除了噪声和晴空大气返回信号外,还有地物、飞鸟等干扰,对于地物、飞鸟等干扰信号采用滤波、飞点剔除等多种方法在雷达信号的预处理中进行了删除,系统输出的大气返回信号功率谱数据中主要包括晴空大气返回信号谱和雷达系统的噪声谱两部分,其中雷达系统的噪声谱主要来自雷达天线接收机元器件的热噪声及雷达系统的相位噪声。
1.1 晴空大气返回信号的谱分布特征大气中的湍流运动形成的折射指数随机不均匀分布对电磁波的散射是风廓线雷达探测大气的基础[1]。湍流形成返回信号不同于点目标,是取样体积内不同尺度湍流团散射的综合作用结果,因此回波信号的功率谱密度分布不是集中在单一谱线上,而是呈现为一定的宽度分布。图 1给出了大气返回信号功率谱密度与谱参数的示意图。
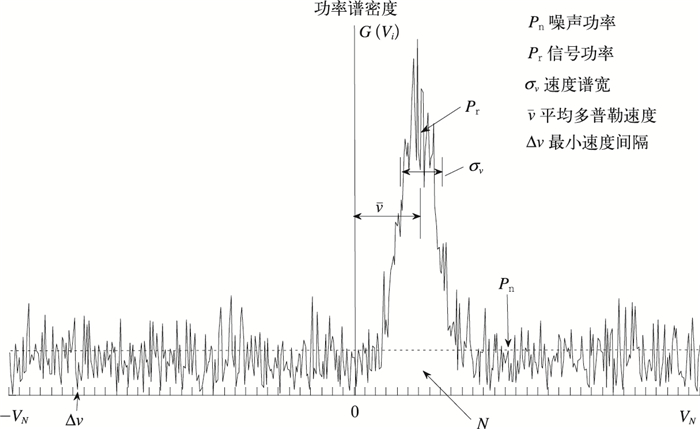
|
|
| 图 1. 大气返回信号功率谱密度谱分布和谱参数示意图 Fig 1. Atmospheric return signal power spectral density distribution and spectrum parameters | |
晴空大气返回信号功率谱密度G(vi) 的零阶矩Pr为大气返回信号的功率,
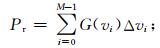
|
(1) |
一阶矩v为大气运动平均多普勒速度,
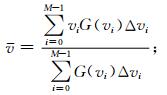
|
(2) |
二阶矩σv为大气运动的多普勒速度谱宽,
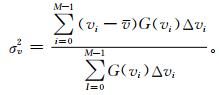
|
(3) |
大气返回信号的统计特征由谱参数Pr,v,σv表征,Pr反映了返回信号的强弱,v表示返回信号相对雷达的径向速度,σv则表示大气运动的涨落特征,σv通常为1~2 m·s-1 [15]。
通常认为大气返回信号的功率谱密度G(vi) 近似为高斯分布,返回信号的谱分布用估算出的Pr,v,σv谱参数来拟合,高斯分布GH(vi) 表达式为
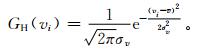
|
(4) |
对大气返回信号谱分布符合高斯分布的程度,应用实测返回信号谱G(vi) 与拟合高斯谱GH(vi) 相对均方根误差λ来表示,定义如下:
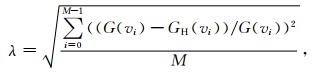
|
(5) |
其中,M是返回信号所在区间范围内谱线数。
利用延庆 (40°27′00″N,115°58′00″E)、东莞 (22°58′27″N,113°44′17″E) 两地风廓线雷达探测的晴空大气返回信号进行统计分析,表 1给出了对流层II型 (CFL-08) 和边界层 (CFL-03) 风廓线雷达的探测参数。统计中随机分别提取延庆CFL-08风廓线雷达2008年1—9月晴空探测资料和东莞CFL-03风廓线雷达2009年7—12月的晴空探测资料各1500份,对大气返回信号的功率谱分布进行高斯拟合,并对其高斯分布拟合符合程度进行检验。实测晴空大气返回信号的谱分布较好地服从高斯分布。延庆地区1500份探测样本的均方根误差为0.11,东莞地区的均方根误差为0.13,80%以上探测样本的相对均方根误差小于0.2。延庆和东莞两地晴空大气返回信号的平均谱宽分别为1.46 m·s-1和1.47 m·s-1,基本相同。马建立[16]对北京延庆地区2006年10—12月15000份晴空大气返回信号资料的统计分析也得出相同结果。
|
|
表 1 风廓线雷达系统参数表 Table 1 System parameters of wind profile radar |
1.2 系统噪声功率谱的统计特征
雷达的系统噪声通常为高斯白噪声[17],多普勒天气雷达和风廓线雷达的系统噪声基本上也为高斯白噪声[18-19]。统计意义上噪声谱线幅度在频带范围内为均匀分布,瞬间噪声谱线幅度的概率分布呈高斯分布,表达式如下:
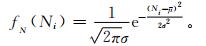
|
(6) |
式 (6) 中,Ni为噪声离散谱线幅度值,fN(Ni) 为Ni幅度的概率密度,噪声谱线幅度平均值μ=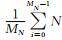
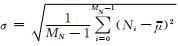
对延庆CFL-08风廓线雷达和东莞CFL-03风廓线雷达的噪声谱线幅度特征进行了统计分析。从CFL-08风廓线雷达和CFL-03风廓线雷达晴空大气高模式探测资料中分别随机选取了1000组噪声谱线数据,每组数据由垂直指向波束探测谱数据中无明显回波信号时的5个连续最远距离库的数据组成,视为噪声谱数据。当FFT点数为512时,则无大气返回信号的噪声谱数据由5×512个数据组成[16]。对每种型号的雷达的5000组数据进行了平均,其平均值基本相同,表明其噪声幅度相同,CFL-08和CFL-03两种风廓线雷达均呈现出白噪声分布特征,但是不同型号雷达噪声幅度的平均值不同,可能与雷达本身的内部结构有关。
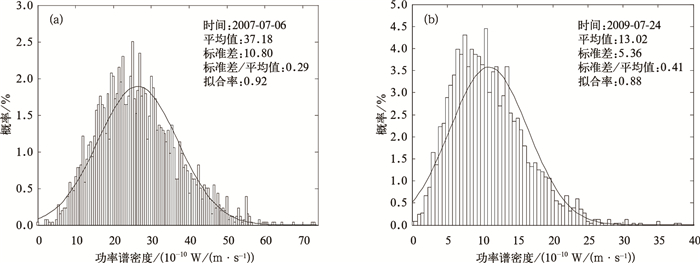
对每组5×512个噪声谱线幅度值的概率分布进行了统计,图 2分别给出延庆CFL-08和东莞CFL-03风廓线雷达某组噪声谱线幅度的概率分布直方图,并给出了拟合的高斯分布和高斯分布的拟合均方根误差λN,表达式为
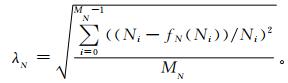
|
(7) |
|
|
| 图 2. CFL-08风廓线雷达 (a) 和CFL-03风廓线雷达 (b)5个距离库噪声特性统计 Fig 2. Noise characteristics of five range bins of CFL-08(a) and CFL-03(b) wind profile radars | |
延庆CFL-08风廓线雷达的1000组数据中有超过86%的数据的均方根误差λN小于0.14,平均值为0.13,东莞CFL-03风廓线雷达1000组数据中93%以上的数据的均方根误差λN小于0.2,平均值为0.11,表明两种型号的风廓线雷达噪声谱线幅度的概率分布基本符合高斯分布,噪声基本为高斯白噪声,两个型号的雷达噪声谱线幅度分布涨落的程度不相同,用雷达噪声的概率分布宽度σ来表示,CFL-08风廓线雷达噪声谱线幅度的涨落程度要大一些。雷达噪声的概率分布宽度σ与噪声谱线的平均幅度 (噪声电平) 的比值 (σ/μ) 基本为一常数,CFL-08风廓线雷达为0.286,CFL-03风廓线雷达为0.412。
CFL-08风廓线雷达和CFL-03风廓线雷达均采用了相控阵天线,但CFL-03风廓线雷达采用了集中式的发射/接收机 (单个T/R),CFL-08风廓线雷达则采用了部分分布式发射/接收机 (多个T/R),CFL-08风廓线雷达的接收机信号是由多个T/R输出综合而成,系统的噪声系数仍为2 dB左右,与CFL-03风廓线雷达相近,噪声功率相当,而噪声谱线幅度的涨落程度却由于多个T/R输出的综合而有所减少,这可能是CFL-08风廓线雷达的σ/μ比CFL-03风廓线雷达要小的原因。
2 风廓线雷达接收机输出信号模拟风廓线雷达接收机输出的大气返回信号含有噪声,噪声主要来自雷达系统本身噪声,大气返回信号与噪声不相干,接收机输出信号的谱密度为晴空大气返回信号谱密度和噪声谱密度叠加[13]。输出信号的功率谱S(vi),
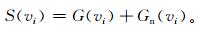
|
(8) |
式 (8) 中,G(vi) 为大气信号谱,Gn(vi) 为噪声谱。在获取了晴空大气谱及雷达系统噪声谱分布规律的统计特征之后,对接收机输出信号谱的仿真模拟可以分成两部分进行:晴空大气信号的仿真以及雷达系统噪声谱的仿真。
2.1 风廓线雷达系统噪声的仿真模拟风廓线雷达的噪声功率谱模拟根据林德贝格-勒维 (Lindeberg-levy) 中心极限定理,认为n个互相独立、同分布且存在平均值与期望的随机变量,其和服从渐近正态分布[20],采用n个在 (0,1) 区间上的均匀分布随机数ζi构造一个随机函数Fi,
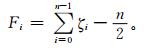
|
(9) |
当n=12时,Fi的期望值为1/2,方差为1/12,认为随机函数服从标准正态分布[21]。
根据式 (9),构造近似符合正态分布的噪声谱分布随机函数Gn(vi),噪声谱线幅度平均值μ定义为Gn(vi) 的期望值,噪声谱线幅度标准差σ定义为Gn(vi) 的方差,
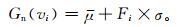
|
(10) |
风廓线雷达的噪声谱线幅度的统计分析表明,延庆CFL-08和东莞CFL-03风廓线雷达的噪声谱线幅度基本服从高斯分布,某一种雷达噪声谱线幅度的标准差与平均值的比σ/μ近似为一常数,变化很小。在确定了拟仿真模拟风廓线雷达型号后,给定雷达系统的噪声谱密度幅度的平均值μ(即噪声电平) 和该型号雷达σ与μ的关系,对噪声功率谱进行仿真模拟。
应用延庆CFL-08风廓线雷达2008年7月12日实测的噪声电平μ和σ/μ值,模拟噪声谱密度分布,如图 3a所示;图 3b是模拟的噪声功率谱密度幅度统计分布直方图与高斯分布,仿真的噪声谱线幅度基本符合高斯分布,利用模拟噪声电平与实测的噪声电平进行1000次的比对试验,相对误差为5%。图 4是利用东莞CFL-03风廓线雷达2009年9月9日的观测数据进行噪声模拟的结果,模拟噪声电平与实测噪声电平相对误差为3%。
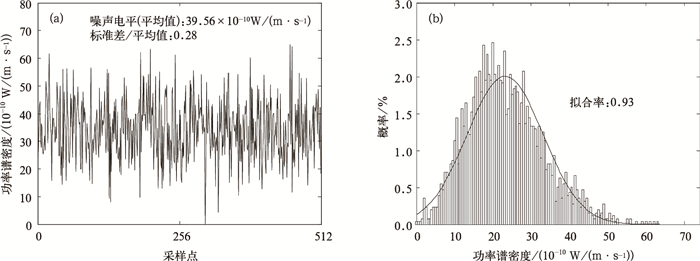
|
|
| 图 3. CFL-08风廓线雷达噪声模拟以及谱线幅度分布 (a) CFL-08风廓线雷达仿真噪声, (b) 噪声高斯拟合特性统计 Fig 3. Noise simulation and spectrum amplitude distribution (a) simulation of noise of CFL-08 wind profile radar, (b) spectrum amplitude distribution | |
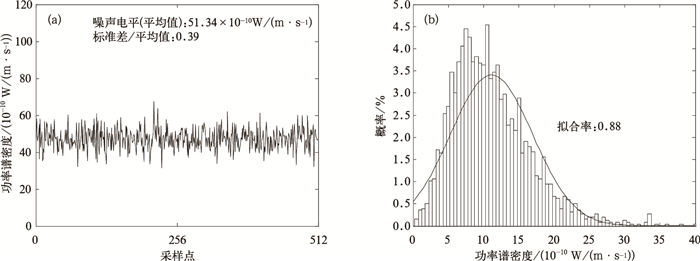
|
|
| 图 4. CFL-03风廓线雷达噪声模拟以及谱线幅度分布 (a) CFL-03风廓线雷达仿真噪声,(b) 噪声高斯拟合特性统计 Fig 4. Noise simulation and spectrum amplitude distribution of CFL-03 wind profile radar (a) simulation of noise of CFL-03 wind profile radar, (b) spectrum amplitude distribution | |
2.2 晴空大气信号功率谱模拟
统计意义上,晴空大气返回信号的功率谱是有一定分布宽度的高斯分布,就一次瞬间观测值来讲,谱线的幅度存在着无规涨落。大气返回信号谱密度分布的仿真模拟由两部分组成,首先模拟出具有统计意义的服从高斯分布的谱密度分布,然后再对每一根谱线的幅度进行无规涨落模拟。
将信号功率Pr,平均多普勒速度v和谱宽σv,代入式 (4),得到统计意义上的信号高斯分布谱,再根据雷达系统设定的谱线间隔Δv将高斯分布谱线进行离散化处理。考虑到谱线幅度的无规涨落,由于雷达取样体积存在散射无规分布和无规运动,其返回信号的涨落可用谱类似噪声幅度涨落的方式表示,运用实际大气返回信号拟合高斯分布的均方根误差λ对每根谱线的幅度进行随机化处理,得到仿真的大气返回信号模拟谱。
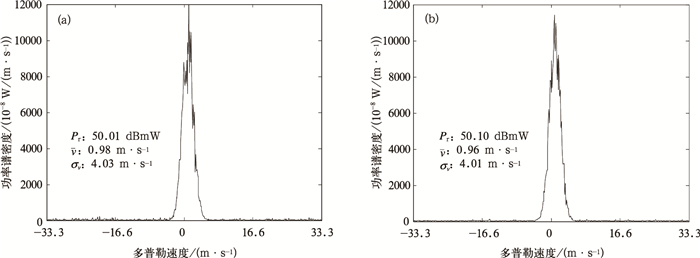
图 5是对大气返回信号的仿真模拟,图 5a是CFL-08风廓线雷达2007年7月6日23:06:58第23个距离库实测的大气返回信号谱密度分布,图 5a中给出了由实测功率谱密度分布估算的谱参数;图 5b是由估算出的谱参数仿真模拟出信号谱分布,标注的谱参数由仿真信号谱密度分布估算得到,可以看出仿真的谱分布与实测的谱分布基本相同,谱参数基本相似。
|
|
| 图 5. 晴空大气返回信号模拟 (a) 实测功率谱,(b) 模拟功率谱 Fig 5. Simulation of return signal of the clear air (a) the power spectrum of observation, (b) the power spectrum of simulation | |
对延庆CFL-08风廓线雷达和东莞CFL-03风廓线雷达实测的大气返回信号谱进行了1000次的仿真模拟比较,CFL-08风廓线雷达信号模拟仿真信号功率相对误差平均值为2%,平均多普勒速度相对误差平均值为3%,谱宽相对误差平均值为1%;CFL-03风廓线雷达探测信号的仿真比较也基本相同,模拟仿真信号功率相对误差平均值为3%,平均多普勒速度相对误差平均值为2%,谱宽相对误差平均值为2%。采用以上方法对风廓线雷达探测大气返回信号谱的仿真模拟结果比较稳定,由仿真模拟谱计算得到的谱参数与实测值相比误差很小。
2.3 模拟信号功率谱密度定标噪声谱密度模拟由平均值 (噪声电平) 和涨落的均方根误差来确定,其模拟的噪声码值Dni的定量描述由噪声功率确定,表达式为
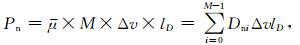
|
(11) |
式 (11) 中,lD为噪声谱的码值,μ为噪声电平,M为采样点数。
大气返回信号功率谱仿真由信号功率Pr、平均多普勒速度v和谱宽σv来确定,模拟返回信号的谱密度的码值Ds的定量描述由信号功率Pr确定,表达式为
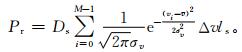
|
(12) |
其中,ls为信号谱的码值。
接收机输出的信号是大气返回信号和系统噪声功率谱密度的合成量,模拟的大气返回信号谱密度和系统噪声谱密度的码值单位应具有一致性的表达。在确定了两种模拟信号中的一种码值的定量描述后,另一种谱输出的单位即可作出相应修订,修订公式由lD=ls,导出
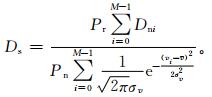
|
(13) |
码值单位修正后,模拟的大气返回信号谱密度与系统噪声的谱密度单位得到了统一。
2.4 大气返回信号谱仿真数据生成流程在给出大气返回信号的信号功率Pr、平均多普勒速度v和速度谱宽σv以及雷达系统噪声功率Pn,设定谱密度分布中码值单位后便可模拟出雷达接收机输出的大气返回信号和雷达系统噪声的谱密度分布,图 6是大气返回信号仿真模拟的流程图。
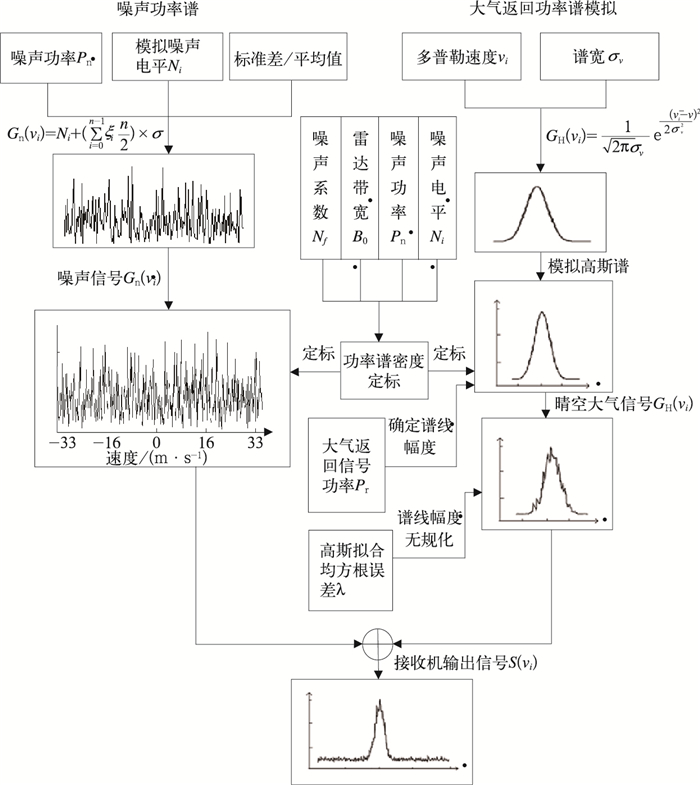
|
|
| 图 6. 风廓线雷达大气返回信号模拟流程图 Fig 6. Flow chart of wind profile radar atmospheric return simulation signal | |
3 仿真谱数据应用
采用上述谱数据仿真生成方法,由回波信号的功率、平均速度、速度谱宽及信号的信噪比等参数构造了大气返回信号谱密度分布仿真数据,对风廓线雷达系统使用的几种信号处理方法进行评估,同时对谱参数估算精度进行分析,应用实例如下。
3.1 噪声电平估算精度的评估风廓线雷达对返回信号功率估算常通过频域中对信号的信噪比和噪声电平的估算来获得,噪声电平的正确确认直接影响到信噪比的输出,进而影响回波功率和大气折射率结构常数 (Cn2) 估算的准确性。雷达系统噪声不可避免地混在雷达输出的信号功率谱密度分布中,如何正确地估算噪声电平至关重要。Hildebrand等[18]提出了客观噪声电平切割法,确定噪声电平,方法较为繁琐,且存在阈值的选取问题;而一般风廓线雷达设备选取噪声电平时常采用一种方法是利用Nyquist速度附近的一定数量的谱线视作噪声来估算噪声电平。通过模拟噪声的仿真数据,评估谱线的抽样数对噪声电平的估算精度的影响。
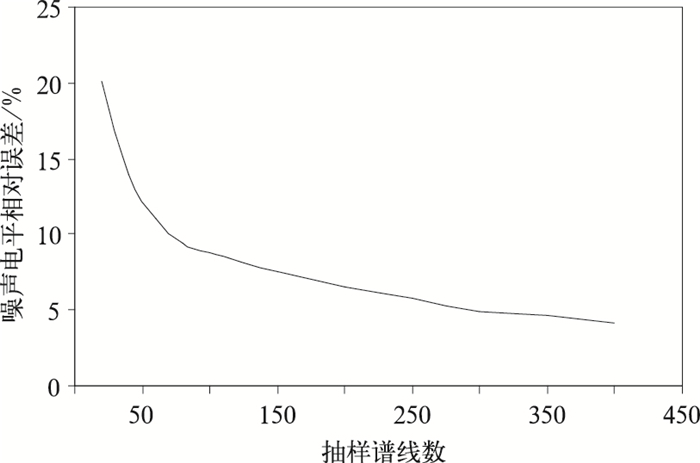
模拟了512根谱线的随机噪声,从中随机抽取若干根谱线计算噪声电平,在20~400范围内共进行了100次不同样本数的模拟计算,与全部谱线计算的噪声电平进行相对误差分析,以确认估算噪声电平的合理取样数。
图 7给出100次估算得出噪声电平相对误差与抽样谱线数的关系,随着抽样谱线数减少,噪声电平的相对误差增大,当抽取的采样点数大于100时,噪声电平的相对误差均控制在8%以内,噪声电平估算的误差为0.5 dB。选取50根谱线,噪声电平估算误差为1 dB。在Nyquist速度附近取50~100根谱线平均值作为噪声电平,估算精度是可取的。
|
|
| 图 7. 噪声电平估算误差与抽样谱线数关系图 Fig 7. Relations between estimation relative error of noise level and numbers of spectral lines | |
3.2 信噪比对谱宽估算影响的评估
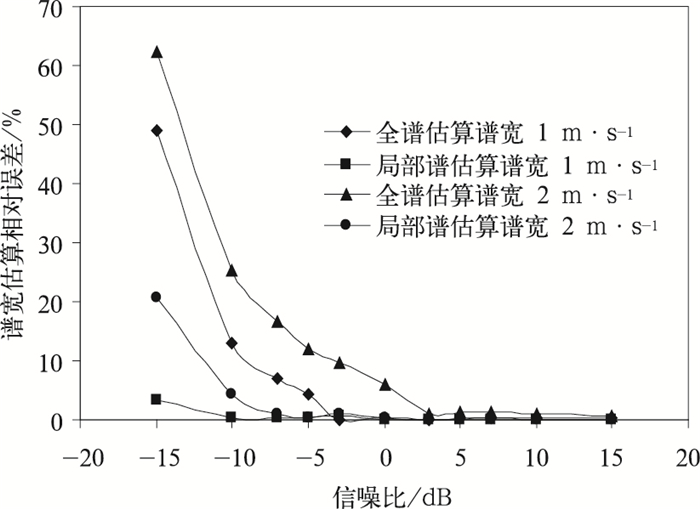
大气返回信号谱宽较好地反映了大气湍流状况,但在频域中对谱宽的估算,受到噪声影响。经典估算谱宽方法是接收到的返回信号谱分布在整个频带范围内积分,为了减少噪声的影响,也常采用局部谱积分的方法,首先是在返回信号谱分布中估算噪声电平,然后由噪声电平确定出大气返回信号的谱线范围,进而估算谱宽。风廓线雷达信号在时域与频域转换过程中,进行了相干积累, 提高相干信号的探测能力。大气返回信号是相干信号, 其探测能力由Nyquist速度和信号谱宽确定,当Nyquist采样速度为±33.3 m·s-1,谱宽为1 m·s-1时最小探测能力为-18.32 dB;谱宽为2 m·s-1时最小探测能力为-15.22 dB。通过建立仿真的大气返回信号 (含噪声) 谱数据,分析信噪比在±15 dB范围内全谱估算和局部谱估算噪声对谱宽估算的影响。
图 8给出了谱宽为1 m·s-1和2 m·s-1两种情况下信噪比对谱宽估算的影响,可以看到信噪比在0以上时,估算谱宽的相对误差趋近于零,噪声对谱宽的估算没有影响,随着信噪比下降,估算谱宽的误差增大,降到-5 dB以下时,均方根误差明显增大。全谱积分时噪声影响大,存在较大的计算误差,局部谱积分方法能够减少噪声对估算谱宽的影响。
|
|
| 图 8. 谱宽计算误差随信噪比的变化情况 Fig 8. Estimation relative error of spectral width with different SNR | |
3.3 半功率点估算谱宽的误差分析
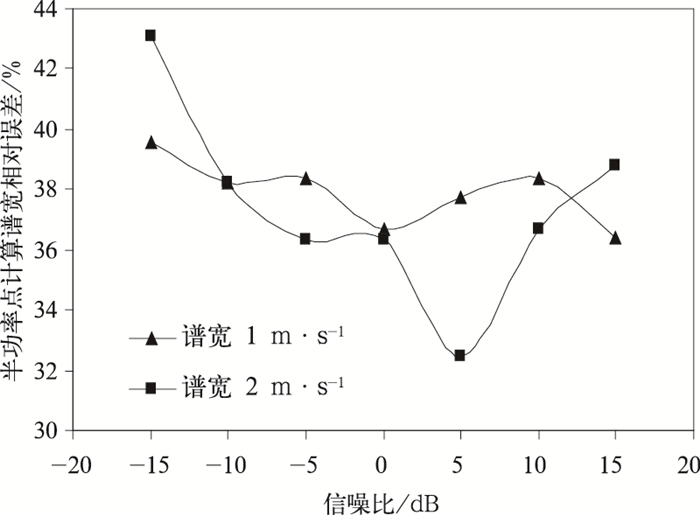
风廓线雷达的信号处理方案中通常为了简化对谱宽的估算,一般对返回信号谱分布进行滑动平均后,采用半功率点方法进行谱宽估算。设定信噪比后,在谱宽为1 m·s-1和2 m·s-1两种情况下,建立仿真的大气返回信号模型,对仿真信号经过五点滑动平均后,用半功率点方法估算谱宽,并对100次的估算值与设定的谱宽计算均方根误差,分析不同信噪比情况下采用半功率点方法估算谱宽的影响。
图 9给出的是用半功率点估算谱宽相对误差随信噪比变化情况。在信噪比为±15 dB之间估算的谱宽相对误差在35%~45%附近变化明显,误差较大。
|
|
| 图 9. 随信噪比不同半功率点计算谱宽误差 Fig 9. Relative error of spectral width with different SNR calculated by the method of half-power point | |
4 小结
1) 利用延庆CFL-08风廓线雷达和东莞CFL-03风廓线雷达的实测资料对大气返回信号的谱分布统计特征进行分析,基本呈高斯分布,谱宽为1.4~1.5 m·s-1;雷达系统噪声是白噪声,其谱线幅度分布符合高斯分布。
2) 采用生成高斯分布随机函数的方法对雷达输出大气返回信号功率谱密度进行模拟,用实测大气返回信号的谱参数与由其仿真的模拟信号谱参数进行1000次的比对,延庆雷达信号模拟仿真信号功率相对误差平均值为2%,平均多普勒速度相对误差平均值为3%,谱宽相对误差平均值为1%;东莞雷达模拟仿真信号功率相对误差平均值为3%,平均多普勒速度相对误差平均值为2%,谱宽相对误差平均值为2%。仿真的功率谱密度分布与实测数据的功率谱密度分布基本相似。
3) 应用仿真信号对噪声电平估算精度及信号的信噪比对谱宽估算的影响进行应用试验表明,仿真信号是评估大气返回信号谱参数的估算精度、优化谱参数估算方法的有用工具。
| [1] | 何平. 相控阵风廓线雷达. 北京: 气象出版社, 2006: 3–24. |
| [2] | 何平, 朱小燕, 阮征, 等. 风廓线雷达探测降水过程的初步研究. 应用气象学报, 2009, 20, (4): 445–470. |
| [3] | 阮征, 葛润生, 吴志根. 风廓线仪探测降水云体结构方法的研究. 应用气象学报, 2002, 13, (5): 170–179. |
| [4] | 阮征, 何平, 葛润生. 风廓线雷达对大气折射率结构常数的探测研究. 大气科学, 2008, 32, (1): 133–140. |
| [5] | 刘淑媛, 郑永光, 陶祖钰. 利用风廓线雷达资料分析低空急流的脉动与暴雨关系. 热带气象学报, 2003, 19, (3): 63–68. |
| [6] | 王令, 郑国光, 康玉霞, 等. 多普勒天气雷达径向速度图上的雹云特征. 应用气象学报, 2006, 17, (3): 281–286. |
| [7] | 李华宏, 薛纪善, 王曼, 等. 多普勒雷达风廓线的反演及变分同化试验. 应用气象学报, 2007, 18, (1): 50–57. |
| [8] | 罗倩, 闫鸿慧. 相关地杂波建模和仿真. 舰船电子工程, 2008, 172, (10): 129–131. DOI:10.3969/j.issn.1627-9730.2008.10.037 |
| [9] | 刘瑞平, 沈福民. 雨杂波的特性及仿真. 火控雷达技术, 2005, 34, (1): 43–46. |
| [10] | 单娜, 冀振元. 舰载超视距海杂波仿真. 现代雷达, 2003, 9, (9): 16–18. |
| [11] | 卢建奇, 赵拥军. 基于ZMNL的雷达杂波仿真研究. 电子对抗, 2006, (2): 31–35. |
| [12] | 邹小海, 韩宏伟, 华祖耀. 雷达模拟器中地物杂波信号仿真的方法研究. 计算机仿真, 2007, 24, (6): 280–283. |
| [13] | 高志球, 肖艳姣, 袁立功, 等. 天气多普勒雷达回波信号处理的模拟实验. 遥感技术与应用, 1998, 12, (4): 43–49. DOI:10.11873/j.issn.1004-0323.1998.4.43 |
| [14] | 钟刘军, 阮征, 葛润生, 等. 风廓线雷达回波信号强度定标方法. 应用气象学报, 2010, 21, (5): 598–605. |
| [15] | Strauch R G, Merritt D A, Moran K P, et al. The colorado wind-profiling network. J Atmos Ocean Technol, 1984, 3, (1): 37–49. |
| [16] | 马建立. 风廓线雷达谱参数提取方法的研究. 成都: 成都信息工程学院, 2008. |
| [17] | 樊昌信, 曹立娜. 通信原理. 南京: 国防工业出版社, 2006. |
| [18] | Hildebrand P H, Sekhon R S. Objective determination of the noise level in Doppler spectra. J Appl Meteor, 1974, 10: 808–811. |
| [19] | Petitdidier M, Amadou S, Garrouste A, et al. Statistical characteristics of the noise power spectral density in UHF and VHF wind profilers. Radio Sci, 1997, 32: 1229–1247. DOI:10.1029/97RS00250 |
| [20] | 石辅天, 唐青松, 李友国. 概率论与数理统计. 沈阳: 东北大学出版社, 2009: 50–51. |
| [21] | 戴颖, 计奎. 生成正态分布随机数的一种新方法——基于Windows时间函数. 地矿测绘, 2004, 20, (2): 7–8. |
 2012, 23 (1): 20-29
2012, 23 (1): 20-29



