2. 国家气象中心,北京 100081;
3. 中国气象科学研究院,北京 100081
2. National Meteorological Center, Beijing 100081;
3. Chinese Academy of Meteorological Sciences, Beijing 100081
卫星云导风,国际上通常称为大气运动矢量 (AMVs, atmospheric motion vectors),国内通常称为云导风或云迹风。卫星云导风资料具有覆盖范围广、时空密度大等优点,因此,它能有效地弥补海洋、高原等地区观测信息的不足,为天气分析和数值预报提供大量有用的资料[1]。
随着卫星探测技术的发展,20世纪90年代末,在传统的红外通道基础上加强了对可见光通道和水汽通道云导风的追踪观测,卫星云导风资料在数量和质量上有了进一步提高[2-3]。国家卫星气象中心早期的工作是用红外通道和水汽通道辐射测值的线性相关特征,粗判图像块是高云还是低云,从而使非常薄的卷云得到运用[4-5]。由于国家卫星气象中心的算法中保留了大量的薄卷云,因此,FY-2E气象卫星云导风 (以下简称FY-2E云导风) 的分布均匀度明显好于其他卫星云导风产品。如何有效应用FY-2E云导风来改善数值预报模式初始场则很有研究价值。
我国现有的同化系统缺乏对FY-2E云导风资料质量系统性的研究工作,例如,观测误差采用的是以往欧洲中期天气预报中心对其他卫星云导风统计得到的,不一定适合FY-2E云导风。因此,非常有必要采用合理的方法来优化三维变分同化系统云导风模块中的各项参数。这对数值预报研究而言,是一项非常重要的基础性工作。
1 云导风反演原理及存在的问题卫星云导风的反演,就是通过一段时间内的连续3幅卫星图像,采用相关系数法追踪云与水蒸气分布图型的模板图像随大气的流动而得到。这种方法被称之为交叉相关法。追踪物的水平运动用几何方法很容易就能求出[6-7],而它所在的垂直高度则一直难以准确得到,特别是对于半透明云 (如薄卷云) 的高度指定比较困难,一般采用窗区 (红外通道) 和吸收区 (水汽或二氧化碳吸收通道) 的黑体亮温共同计算得到。这种方法的基本原理最早是由Smith[8]提出的,后来Szejwach[9]首先引入水汽通道作为吸收区,将这种方法用于云导风的高度估计,证明了用两个通道计算得到的云导风高度要比只用红外通道的准确。Nieman等[10]分别对比分析了只用二氧化碳吸收通道指定云顶高度和用双通道法 (红外通道和水汽吸收通道) 指定高度这两种方法的效果,结果表明后者的效果比前者好。目前,国际上仍采用双通道法来指定半透明云的高度。
双通道方法是基于这样的事实:在红外通道和水汽吸收通道中观测得到的来自某一厚度云层的辐射能量随着云量呈线性变化[11]。它将来自半透明云层的辐射换算成相同高度密实云的辐射量,所以在估计半透明卷云的高度时需要知道大气中各个高度上存在密实云时的辐射测值。然后通过双通道散点图截距法就能求得云顶高度,即在红外通道和水汽通道辐射量的二维图上,通过线性外推晴空辐射量与观测辐射量的连线,与不同高度密实云的辐射曲线相交,得到的交叉点就是该云顶高度上密实云的辐射量。最后,根据不同高度密实云的辐射曲线得到相应的云顶高度。
在半透明云的高度指定过程中,需要根据数值预报场的温度和水汽垂直廓线来计算得到来自不同高度密实云的辐射曲线。当数值预报场存在较大误差时,根据数值预报计算得到的密实云辐射值与卫星实际观测到的辐射不匹配,此时计算得到的云导风高度不准确。这是目前云导风产品定高存在误差的主要来源之一。
2 高度变分调整国际上普遍采用云导风的质量标志码QI (quality indicator) 值来作为衡量云导风产品质量好坏的依据。QI值是附加在云导风产品中的一个参考数值,范围在0~1之间,数值越大,其可信度越高。经过统计,发现FY-2E云导风产品的QI值对质量的指示意义比较弱,表现在高QI值对应的速度偏差与均方根误差比较大,如赤道外北半球地区 (20°~65°N,40°~170°E) 高层 (400~250 hPa) 的云导风,QI值在0.85~0.9,0.9~0.95,0.95~1.0共3个范围内与探空资料的的平均偏差分别为-7.62 m·s-1,-6.81 m·s-1,-6.39 m·s-1,标准差分别为10.18 m·s-1,9.45 m·s-1,8.73 m·s-1,虽然有递减的趋势,但偏差仍然很大,无法运用到数值预报业务中。因此,本文采用简单可行的变分方法对云导风产品进行了高度调整工作,并考察了高度误差对云导风产品质量的影响。
2.1 资料与方法 2.1.1 资料统计样本采用2010年5月1日—8月31日00:00(世界时,下同) 和12:00两个时次的FY-2E红外通道云导风资料 (国家卫星气象中心提供) 和探空资料,研究区域范围为65°S~65°N,40°~170°E。探空资料已经过质量控制,主要包括静力学检查、极值检查与空间一致性检查。预报场资料来源于国家气象中心业务运行的T639数值模式的3 h预报。T639资料的气压层从1000 hPa到10 hPa共26层,水平分辨率为0.28125°×0.28125°。统计分析时,按纬度将研究区域划分为3个地理区域:赤道外北半球地区 (20°~65°N)、赤道地区 (20°S~20°N) 和赤道外南半球地区 (20°~65°S)。
2.1.2 高度变分调整法Hayden等[12]采用了最早由Purser等[13]提出的递归滤波客观分析方法,利用12 h预报场资料对云导风进行了高度再指定,进一步提高了云导风产品的质量。递归滤波方法除了具有其他客观分析方法的优点[14-15]之外,还具有局地变尺度的特征,因此特别适合于水平各向异性资料的质量控制。Hayden等[16]在递归滤波的基础上,结合云导风产品的QI值进行质量控制,取得了很好的效果 (QI值≥0.7时,云导风的均方根误差为5.1 m·s-1)。Velden等[3]采用了数值预报场和经递归滤波质量控制后的云导风,根据一个简单的变分目标函数求得风矢量的最小误差值,以此来调整水汽导风的高度,并将GOES-8风场资料 (红外、可见光和水汽3个通道) 同化到NOGAPS全球数值预报模式中,对热带气旋路径进行了预报,效果改善明显。
这里借鉴Velden等[3]的工作,结合FY-2E云导风特征对目标函数进行了改进,将数值模式预报场资料作为辅助信息,在垂直方向上搜索与之相差不大的预报场风矢量,并将之调整到对应的高度。目标函数J(P) 如式 (1) 所示:
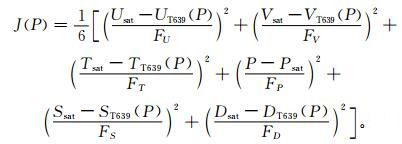
|
(1) |
其中,下标sat表示卫星云导风资料,T639表示T639预报场资料;U, V, T, P, S, D分别为纬向风速、经向风速、温度、气压、全风速大小和风矢量方向角,分母F为经验系数。
考虑到风场在星下点附近的赤道地区观测误差较小,而向两极逐渐增大的特征,经过统计分析,设计了如表 1所示的经验系数。
|
|
表 1 经验系数设置 Table 1 Settings of coefficients |
表 1中经验系数的确定一方面要考虑到能够指定到正确的高度并滤去错误的风矢量,另一方面要减小受预报场的影响程度。纬向风和经向风分量的经验系数不应定得过小,否则会剔除很多有用的云导风,并且云导风会非常靠近预报场。由于赤道地区的观测误差比中高纬度地区的要小,因此相应的经验系数可以定得小些。同时,考虑到中高纬度地区急流轴附近的风向存在较大差异,风向的经验系数可以控制得小些,以减小在反演过程中高层的云导风受急流轴定位偏差的影响程度。以上经验系数是与探空资料相比较得到,由于探空资料的温度存在较多的缺测值,因此这里的温度经验系数定得比较粗糙,确定更为合理的经验系数还有待于进一步的分析和试验。
在进行高度变分调整时,首先采用双线性插值方法,将T639的3 h预报场资料插值到云导风所在经纬度的位置,垂直方向上用三次样条插值得到各个变量的垂直廓线,然后求取上述目标函数J(P) 的极小值。为了考察云导风的系统性偏差,将云导风的调整幅度控制在±250 hPa以内,实际运用时可以控制得更小,以避免不合理的大范围调整。另外,如果目标函数J(P) 的极小值大于1.0,则认为该风矢量错误,舍去。
2.2 效果检验本文采用风速的均方根误差垂直廓线来考察云导风高度的订正情况。以探空站点为中心,在1°×1°范围内搜索距离探空最临近的云导风,用三次样条方法将探空风场插值到与云导风相对应的层次上,相减得到分析样本,在此基础上计算各层云导风的均方根误差。
考察云导风的效果主要从高度的调整情况、散点分布与偏差的频率分布以及偏差与均方根误差的垂直分布3个方面来进行。
2.2.1 高度的调整情况采用上述变分方法进行高度调整后,调整幅度和数量呈现出明显的区域特征:赤道地区云导风调整幅度为-25~40 hPa;赤道外南、北半球地区云导风大多数是向下调整,其中赤道外北半球地区主要集中在100 hPa以内,50°N附近最高达200 hPa。以上事实初步反映出赤道外南、北半球地区云导风产品的高度存在系统性偏高的问题。
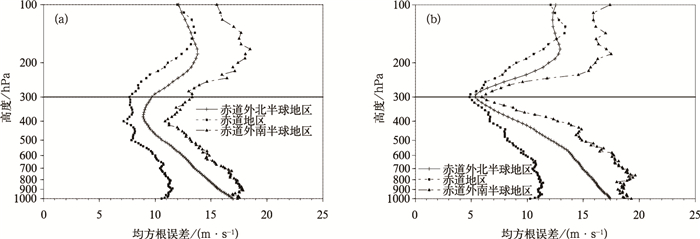
可以认为,如果某层的云导风高度准确,那么和探空风速的偏差的均方根误差在该层次将最小,这在均方根误差垂直廓线图 (图 1) 上表现为对应该层出现一个极小值。经高度调整后,均方根误差极小值准确地出现在300 hPa (如图 1b所示),而高度调整前,极小值出现在约400 hPa附近 (如图 1a所示),表明云导风在反演过程中将大部分风矢量高度定在了高层。定高偏差整体上从高层向低层呈递增的趋势,高层 (400 hPa以上) 的偏差约100 hPa,而中低层 (400 hPa以下) 的将达到150 hPa,这表明云导风的定高存在系统性偏高的问题。
|
|
| 图 1. 300 hPa FY-2E云导风产品与探空资料整层风场的均方根误差垂直廓线 (a) 调整前, (b) 调整后 Fig 1. RMSE profile between 300 hPa FY-2E AMVs and entire profile of collocated radiosonde observations (a) before height adjustment, (b) after height adjustment | |
另一方面,在理想情况下,极小值两侧的曲线应该非常陡,这是因为在云导风反演过程中是将云导风看做单层风场信息来处理的。高度调整前,云导风极小值附近相当平缓,体现不出云导风是单层风场的特点;经高度调整后,极小值附近的曲线非常陡峭,单层风场特征表现明显。
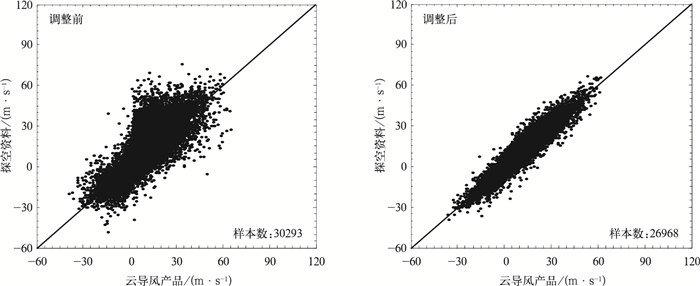
2.2.2 散点分布与偏差的频率分布由赤道外北半球地区400 hPa以上FY-2E云导风产品与探空资料的散点分布图 (图 2) 可以看出,高度调整前,云导风产品的分布相当分散,且与探空资料的偏离较大,多数分布在1:1线的上方,表现出较大的负偏差,经向风分量相对于纬向风分量要好些;高度调整后,尽管数量有所减少,但云导风的分布很集中,整体质量提高了。
|
|
| 图 2. 赤道外北半球50~400 hPa FY-2E云导风产品与探空资料纬向风速散点分布 Fig 2. Scatter plots of zonal wind of FY-2E AMVs against radiosonde observations at 50—400 hPa in the North Hemisphere extra-tropics | |
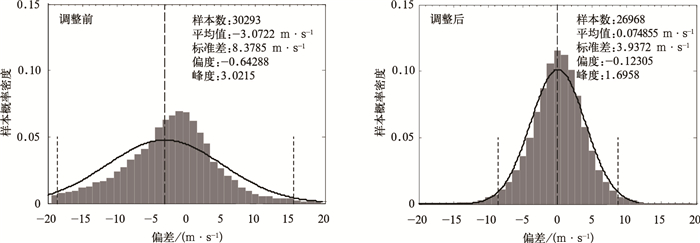
从赤道外北半球地区400 hPa以上FY-2E云导风产品与探空资料风速偏差的样本概率分布图 (图 3) 看到,调整前后,云导风纬向风分量的标准差分别为8.3785 m·s-1和3.9372 m·s-1,减小幅度超过一半。并且纬向风分量的负偏差得到了改善,峰度数值减小幅度将近1.5,其概率分布形态的陡缓程度与正态分布更加相近,能够满足三维变分同化方法中高斯分布的假设。
|
|
| 图 3. 赤道外北半球地区50~400 hPa FY-2E云导风产品与探空资料纬向风风速偏差的样本概率分布 (光滑曲线为正态分布曲线,长虚线为平均值,两短虚线分别为μ±2σ) Fig 3. Probability distribution of zonal wind speed deviation of FY-2E AMVs to radiosonde observations at 50—400 hPa in the Northern Hemisphere extra-tropics (smooth curve is normal distribution curve, long dashed line is mean value, two short dashed lines are μ±2σ, respectively) | |
2.2.3 偏差与均方根误差的垂直分布
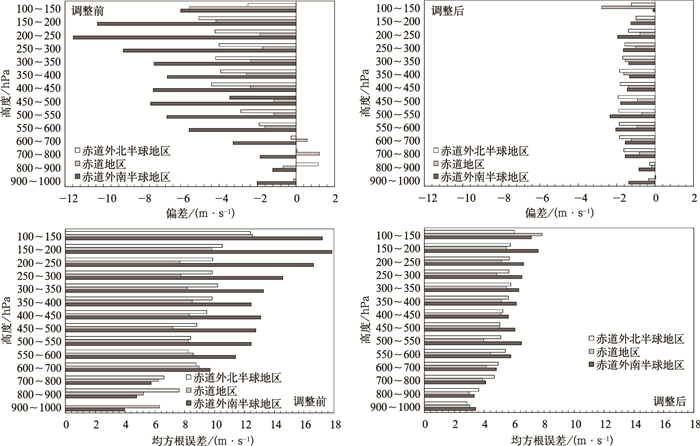
如图 4所示,高度调整后,各层云导风风速平均偏差和均方根误差均明显减小,分别控制在2 m·s-1和6.5 m·s-1以内,且在空间和时间上分布稳定。即FY-2E云导风产品经高度调整后质量有了明显提高。
|
|
| 图 4. 高度调整前后FY-2E云导风产品与探空资料全风速偏差和均方根误差的垂直分布 Fig 4. Speed bias and RMSE of FY-2E AMVs calculated before height adjustment and after height adjustment against radiosonde observations at each height level | |
高度调整前,风速在高层出现明显的负偏差,在对流层附近最大,南半球最为明显,达到-10 m·s-1。由以上分析结果可见,出现这种情况的原因在于很多低层的云导风被错误地指定到了高层,而实际大气中低层的风速往往比高层的小。将高层200~300 hPa的云导风向下调整之后,质量有提高,以南半球最为明显,其各层全风速的平均偏差从原来的-10 m·s-1大幅减小到-2 m·s-1以内,均方根误差也从原来的16 m·s-1减小到7 m·s-1以内。
2.3 方法的优缺点采用变分法,通过一个极小化运算,一方面调整了云导风的高度,另一方面去除了偏差较大的资料,优点在于简单明了,不需要深入研究云导风反演算法。同时,该方法也存在缺陷:一方面,目标函数里的经验系数是对一段时间的资料统计得到的,并不适合任意时间段的云导风高度调整;另一方面,它依赖于数值预报场的质量,在预报场质量差的情况下,很多质量好的资料很可能在上述极小化过程中被丢弃,也有可能被指定到错误的高度上,影响资料的整体质量。
该方法在现有云导风基础上进行,并没有从反演角度解决云导风的定高问题,但是该方法为云导风在数值天气预报中的应用提供了一条简单而有效的途径。云导风产品质量的根本性提高还有赖于对云导风反演过程中的误差来源逐一消除。
3 观测误差方差的准确估计观测误差方差的准确估计非常重要。我国自行研究和发展的GRAPES同化系统中采用的观测误差均方差和质量控制系数大多从国外同化系统中引进,这些参数不完全适合我国的同化系统,也不能准确描述FY-2E云导风产品,因此很有必要对这些参数进行重新计算。
3.1 新息向量法与相关模型对于观测相对密集的资料而言,可以在观测空间利用观测值与背景值之差来分离背景误差和观测误差方差,从而计算得到云导风的观测误差方差,这种方法被称为新息向量法。这是一种最简单、最可靠的估计方法,通常要求观测网稠密,能够提供足够多的信息。这种方法最早是Hollingsworth等[17]和Lonnberg等[18]在前人工作的基础上提出来的,Xu等[19-20]在Hollingsworth等[17]和Lonnberg等[18]的工作基础上,提出了更为合理的正定约束条件。
在观测误差和背景误差之间不相关、观测误差和背景误差都是无偏、观测站点之间观测误差水平不相关和背景误差在水平方向均匀且各向同性的假定下,新息向量的方差可以表示为
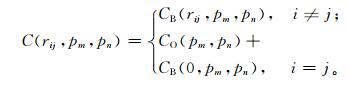
|
(2) |
式 (2) 中,r为两观测站的距离;p表示气压;i, j代表水平层上的两点;m, n代表垂直层上的两点;CO, CB分别为观测场和背景场。
式 (2) 表明,对于同一层上 (m=n) 的资料有:① 在同一观测点 (i=j),新息向量的方差等于观测误差方差与背景误差方差之和;② 在不同观测点上 (i≠j),由于观测误差之间不相关,新息向量的方差等于背景误差方差。因此,只要采用合理的拟合函数,对不同观测点上的背景误差方差进行拟合,外推拟合曲线至距离r=0处即为同一观测点的背景误差,从新息向量总方差中减去背景误差方差即为观测误差,从而实现观测误差和背景误差的分离。新息向量方法依赖于观测资料的密集程度,对于密集的FY-2E云导风产品 (1°×1°),采用该方法显然是合理的。
在云导风追踪反演过程中,如云追踪、高度指定以及质量控制,都会引入空间相关误差,因此,云导风产品纬向风和经向风本身既不是相互独立,也不是各向同性,不满足新息向量法的基本假设条件。对于像云导风这样的矢量场,解决方法是将风矢量写成无辐散涡旋风Vψ和无旋辐散风Vχ之和 (Vψ和Vχ分别用流函数ψ和势函数χ来表示),涡旋风和辐散风都是各向同性的,但并不独立,只有将风矢量分解到两点间连线方向 (即径向l) 和垂直于连线方向 (即切向t) 才能保证两者是各自独立的[20]。在半无限空间0≤r<∞中,经过径向和切向分解后,风矢量的水平二维拟合形式如式 (3) 所示,这里使用的误差方差拟合函数是用Bessel函数构造的[17, 20]:
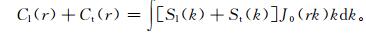
|
(3) |
其中,J0(rk), J2(rk) 分别为零阶和二阶贝塞尔函数,Sl, St分别为背景误差在径向和切向的功率谱。采用Hankel变换即可得到背景误差的功率谱形式:
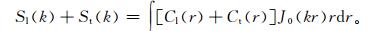
|
(4) |
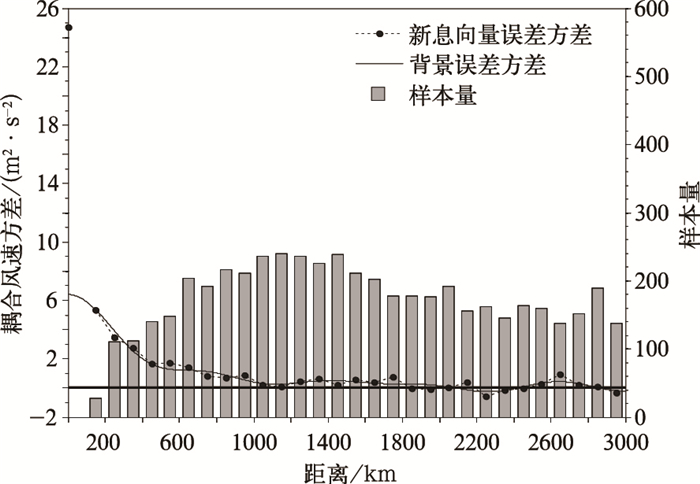
在有限范围内 (r≤D=3000 km),用最小二乘法拟合式 (4),通过联立线性方程组,即可求得功率谱系数Sl(k) 和St(k)。最后,将功率谱系数反代回式 (3) 就得到任意距离r处的背景误差方差,外推拟合曲线至r=0处即为同一观测点的背景误差方差,从新息向量总方差中减去背景误差方差即为观测误差方差。拟合结果如图 5所示。
|
|
| 图 5. 250 hPa新息向量误差方差与拟合的背景误差方差函数曲线 Fig 5. Error variance of innovation vectors and fitted background error variance functions | |
3.2 数据处理和拟合结果
探空资料风场是某一地点的瞬时风场信息,而静止卫星反演得到的云导风是某一区域的平均风场信息。严格地讲,这两种性质不同的风场是无法进行比较的,这里为了简便起见,将云导风作为单点的瞬时风场处理。以探空站点为中心,在1°×1°范围内搜索距离探空最近的云导风 (已经经过高度变分调整),用三次样条方法将探空资料风场插值到与云导风相对应的层次上,然后将每一时间点每一层的云导风产品风速值减去探空风速,得到新息向量。由于假定观测值和背景值均无偏,将新息向量减去每个站点每层的新息向量的时间平均,得到满足假设条件的分析数据,在此基础上求解云导风的观测误差均方差。对云导风产品采用极值检查来排除非气象意义的错误风矢量,垂直层次划分如表 2所示。因为探空资料的误差方差样本点空间分布不均匀,为了更好地进行拟合,将样本按站点间距离每隔100 km进行划分,共30组。
|
|
表 2 垂直层次的划分 Table 2 The partition of vertical levels |
用上述方法分析拟合之后,得到如表 3所示的各层云导风的观测误差均方差。计算得到的云导风观测误差均方差比GRAPES原三维变分模块中用的偏大1~1.5 m·s-1,但上述方法是在观测资料不相关的基础上进行的,实际的云导风观测资料存在相关,为了削弱这种相关的影响,一方面对所有的云导风资料都按2°×2°的格距进行了稀疏化工作,另一方面采用了放大观测误差的方法,在统计计算得到的观测误差的基础上放大2~2.8 m·s-1。
|
|
表 3 各层云导风的观测误差均方差 (单位:m·s-1) Table 3 Observation errors of AMVs at each level (unit:m·s-1) |
3.3 质量控制参数
由于目前云导风的质量标志码QI的指示意义比较弱,这里只采用了背景场检验的方法来进行质量控制。方法是将每个云导风的纬向风和经向风分量,分别与背景场插值到该观测位置的值进行比较,计算出两者之间的差值,如果这个差值超过了最大的阈值,则予以剔除。这个阈值L为云导风纬向风和经向风分量控制系数qc与观测误差εo的乘积。
以400 hPa以上高层云导风纬向风分量为例,调整后偏差的样本数量在0附近最多,样本平均值μ为0.074855 m·s-1,均方差σ为3.9372 m·s-1,图 3中的曲线为理论上服从N(μ, σ2) 的正态分布概率曲线。根据正态分布函数理论,落在 (μ-2σ, μ+2σ) 内的样本数量可达到总数的95.44%。经过上述云导风观测误差的计算,高层云导风的观测误差一般在4.65 m·s-1附近,根据式 (5)qc的值可以近似定为1.7。
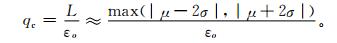
|
(5) |
为了对比分析加入云导风产品高度调整前后对GRAPES全球模式预报效果的影响,设计了4个数值试验方案。
控制试验 (CTRL):使用的资料是采用国家气象中心业务模式T213的18 h预报场资料以及探空、地面、飞机和船舶观测资料。
对比试验1(TEST1):在控制试验的基础上添加高度变分调整前的云导风观测资料,观测误差方案为表 3中的旧方案观测误差。
对比试验2(TEST2):在控制试验的基础上添加高度变分调整后的云导风观测资料,观测误差方案为表 3中的旧方案观测误差。
对比试验3(TEST3):在控制试验的基础上添加高度变分调整后的云导风观测资料,观测误差方案为表 3中的新方案观测误差。
在采用GRAPES全球模式进行预报时,全部采用相同的物理参数化方案,总共进行了为期15 d (共30个) 的预报试验 (2010年8月28日00:00—9月11日12:00),每个试验每6 h输出1次预报结果,向前预报7 d,并分别与该预报时刻的GRAPES三维变分分析场作对比分析,分析区域为90°S~90°N, 40°~170°E, 水平格距为1°×1°。
4.2 试验结果分析这里,为了对比3个试验的预报效果,本文采用改进率I来衡量试验的改进效果,公式如下:
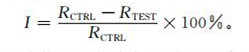
|
(6) |
式 (6) 中,R为物理量的均方根误差,下标CTRL和TEST分别代表控制试验和对比试验。I为正时,对比试验的均方根误差小于控制试验的,表明为正效果;反之,为负效果。
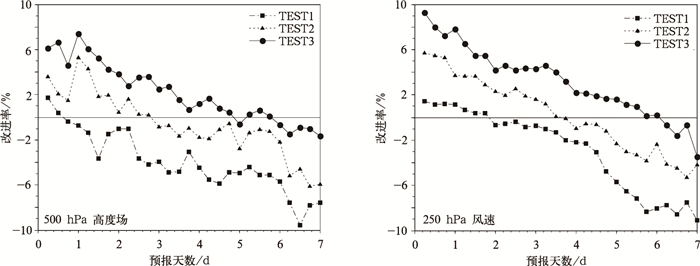
如图 6所示,试验结果表明,TEST3方案明显比其他两个方案好;TEST2方案由于设定的观测误差较小,一方面滤去了比较好的资料,另一方面使云导风产品存在较大的相关性,因此效果比不上TEST3方案;TEST1方案由于高度不准,云导风误差较大,因此效果最差。经过高度调整后的云导风产品对北半球区域的短期预报 (1~3 d) 有正的预报效果,其中风场在400 hPa以上改进效果较明显,其预报时效可以达到6 d,而低层物理量的改善效果没有高层明显,这是因为云导风资料主要集中在高层,对高层的影响最大;南半球也有正的预报效果,但改进的幅度较北半球小 (地面气压在1.5%以内,温度场在2%以内,高度场和风场在4%以内),这和上述高度调整法所采用的背景场的质量好坏有关。
|
|
| 图 6. 北半球区域 (0°~90°N, 40°~170°E) 数值试验的预报改进率 Fig 6. Rate of forecast experiment improvement in the region of the North Hemisphere (0°—90°N, 40°E—170°E) | |
5 小结与讨论
目前,FY-2E云导风产品误差比较大,主要原因是云导风高度指定不准确。针对这一问题,采用了一维变分方法对云导风高度进行调整,分析表明,经过调整高度后,云导风产品质量得到了很大提高。在此基础上用新息向量法求得云导风的观测误差,并采用稀疏化和扩大观测误差的方法消弱云导风观测资料之间的相关性影响。最后,运用GRAPES全球模式,设计了数值试验方案进行模拟,结果表明,GRAPES三维变分模块中对云导风的观测误差设置不合理 (偏小),采用新的观测误差方案后,经过高度调整后的云导风产品能提高数值模式北半球高层的短期预报能力,高层的改进效果明显好于中低层;南半球的改善效果没有北半球改善明显,原因可能是在高度调整过程中采用的数值预报场在南半球的误差较大。
以上分析表明,云导风的定高误差是亟需解决的首要问题,它直接影响到云导风在数值模式中的应用效果。云导风的制作者认为,高度指定存在系统性偏高的问题,主要有以下两方面的原因:一方面,就目前所采用的双通道定高方法而言,薄卷云的观测辐射量中很大的一部分来自地面,但是来自地表的辐射难以求准确,表现为薄卷云的红外通道和水汽通道辐射统计关系中斜率求不准,地表辐射剔除得是否干净,是提高云导风定高准确性的关键因素之一;另一方面,在云导风制作过程中需要数值预报系统提供预报场资料,数值预报场的误差将被引入到云导风产品中,尤其在观测资料缺乏的大洋上,这部分误差也是目前云导风产品高度指定存在误差的来源之一。
如上所述,云导风反演的误差与数值预报场的精度密切相关,数值预报系统需要云导风产品来调整模式变量间的平衡,以提高预报能力;云导风的反演需要数值预报系统提供精确的预报场,来提高云导风产品的质量,这两者是相辅相成的。在提高云导风反演精度方面有很多工作值得去做,不仅如此,在资料同化方面也有很多值得改进的地方,这需要在实际工作中不断发现问题,不断完善,只有这样,云导风才能同化到业务数值预报系统中,从而进一步改善数值预报场,提高预报能力。
致谢 FY-2E云导风产品来自于国家卫星气象中心,并得到许健民院士和张其松研究员的很大帮助,在此表示感谢!| [1] | 侯青, 许健民. 卫星导风资料所揭示的对流层上部环流形势与我国夏季主要雨带之间的关系. 应用气象学报, 2006, 17, (2): 138–144. |
| [2] | Ottenbacher A, Tomassini M, Holmlund K, et al. Low-level cloud cotion cinds from meteosat high-resolution visible Imagery. Wea Forecasting, 1997, 12: 175–184. DOI:10.1175/1520-0434(1997)012<0175:LLCMWF>2.0.CO;2 |
| [3] | Velden C S, Olander T L, Wanzong S. The impact of multispectral GOES-8 wind information on Atlantic tropical cyclone track forecasts in 1995. Part I: Dataset methodology, description, and case analysis. Mon Wea Rev, 1998, 126: 1202–1218. DOI:10.1175/1520-0493(1998)126<1202:TIOMGW>2.0.CO;2 |
| [4] | 许健民, 张其松, 方翔. 用红外和水汽两个通道的卫星测值指定云迹风的高度. 气象学报, 1997, 55, (4): 408–417. DOI:10.11676/qxxb1997.041 |
| [5] | Xu J M, Holmlund K, Zhang Q S, et al. Comparison of two schemes for derivation of atmospheric motion vectors. J Geophys Res, 2002, 107, (14): 1–15. |
| [6] | 许健民, 张其松, 王大昌, 等. 云迹风计算中的两个几何问题. 应用气象学报, 1997, 8, (1): 11–18. |
| [7] | 许健民, 张其松. 卫星风推导和应用综述. 应用气象学报, 2006, 17, (5): 574–582. |
| [8] | Smith W L. An improved method for calculating tropospheric temperature and moisture from satellite radiometer measurements. Mon Wea Rev, 1968, 96: 387–396. DOI:10.1175/1520-0493(1968)096<0387:AIMFCT>2.0.CO;2 |
| [9] | Szejwach G. Determination of semi-transparent cirrus cloud temperature from infrared radiances: Application to METEOSAT. J Appl Meteor, 1982, 21: 384–393. DOI:10.1175/1520-0450(1982)021<0384:DOSTCC>2.0.CO;2 |
| [10] | Nieman S J, Schmetz J, Menzel W P. A comparison of several techniques to assign heights to cloud tracers. J Appl Meteor, 1993, 32: 1559–1568. DOI:10.1175/1520-0450(1993)032<1559:ACOSTT>2.0.CO;2 |
| [11] | Schmetz J, Kenneth H, Joel H, et al. Operational cloud-motion winds from meteosat infrared images. J Appl Meteor, 1993, 32: 1206–1225. DOI:10.1175/1520-0450(1993)032<1206:OCMWFM>2.0.CO;2 |
| [12] | Hayden C M, Velden C S. Quality Control and Assimilation Experiments with Satellite Derived Wind Estimates. Preprints, Ninth Conf on Numerical Weather Prediction. Denver, CO, Amer Meteor Soc, 1991: 19-23. |
| [13] | Purser R J, McQuigg R. A Successive Correction Analysis Scheme Using Recursive Numerical Filter. Met O 11 Tech Note, No. 154, British Meteor Service, 1982: 17. |
| [14] | Cressman G P. An operational objective analysis system. Mon Wea Rev, 1959, 87: 367–374. DOI:10.1175/1520-0493(1959)087<0367:AOOAS>2.0.CO;2 |
| [15] | Barnes S L. A technique for maximizing details in numerical weather map analysis. J Appl Meteor, 1964, 3: 396–409. DOI:10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2 |
| [16] | Hayden C M, Purser R J. Recursive filter objective analysis of meteorological fields: Applications to NESDIS operational processing. J Appl Meteo, 1995, 34: 3–15. DOI:10.1175/1520-0450-34.1.3 |
| [17] | Hollingsworth A, Lönnberg P. The statistical structure of short-range forecast errors as determined from radiosonde data. Part Ⅰ: The wind field.. Tellus, 1986, 38A: 111–136. DOI:10.1111/tela.1986.38A.issue-2 |
| [18] | Lönnberg P, Hollingsworth A. The statistical structure of short-range forecast errors as determined from radiosonde data. Part Ⅱ: The covariance of height and wind errors.. Tellus, 1986, 38A: 137–161. DOI:10.1111/tela.1986.38A.issue-2 |
| [19] | Xu Q, Wei L, Tuyl A V, et al. Estimation of three-dimensional error covariances. Part I: Analysis of height innovation vectors. Mon Wea Rev, 2001, 129: 2126–2135. DOI:10.1175/1520-0493(2001)129<2126:EOTDEC>2.0.CO;2 |
| [20] | Xu Q, Wei L. Estimation of three-dimensional error covariances. Part Ⅱ: Analysis of wind innovation vectors. Mon Wea Rev, 2001, 129: 2939–2954. DOI:10.1175/1520-0493(2001)129<2939:EOTDEC>2.0.CO;2 |
 2011, 22 (6): 681-690
2011, 22 (6): 681-690



