2. 北京市气象局,北京 100089
2. Beijing Meteorological Bureau, Beijing 100089
气象灾害风险区划针对风险地区可能遭受气象灾害影响的严重程度进行风险识别及风险评估,确定不同风险地区的气象灾害风险大小并划分其风险类型及等级。这对气象灾害风险规避及防范、气象安全服务保障体系建设等方面都具有重要的应用价值,近年来在气象灾害应急服务保障、气象服务决策支持业务应用等领域得到较为广泛的应用[1-5]。多数气象灾害风险区划的主要依据是极端天气及气候事件的概率风险,以极端气象要素值出现的概率或重现期来划分风险等级区域,但灾害风险与概率风险是有严格区分的。概率风险的长处是比较容易统计及建立风险等级标准,而灾害风险除了要考虑灾害事件出现的概率,更应该侧重灾害的强度及损失量,比如巨灾在概率上的贡献与中等强度以下的灾害是一样的,体现的风险大小显然不一样。Smith提出的风险评估方程“风险=出现概率×损失量”就明确表示风险是概率与损失的乘积[6]。出于同样目的,黄崇福等在信息扩散理论的基础上计算超越概率来体现不同灾害强度的风险特征,并据此进行风险区划[7]。信息扩散理论将灾害损失情况体现到风险评估中,主要用于弥补风险区划中小样本信息量的不足[8-9],对于样本量比较大的风险评估可酌情使用。在样本较多的条件下,进行类似直方图方法的不同灾损情况下灾害发生频次统计是有必要的[10],这除了能体现评估地区整体灾害危险状况,还能借此确立风险区划等级,达到与概率风险评估一样的效果。
灾害风险系统的变化被认为是非平稳马尔科夫随机过程,结合历史灾情资料进行灾害风险区划的另一个不可忽视的是时间序列条件下灾害事件的损失变异特征的认识和评判[11-12]。高庆华等认为变异系数是反映灾害风险时间变化程度的指标,需要根据不同地区历史灾情统计资料,结合预测风险来分析[13]。Pedro等提出了用于非稳定时间序列突变检测的启发式分割算法 (BG算法)[14],该方法基于滑动t-检验思想,能有效处理非线性、非平衡信号,比较适合基于历史灾情资料的时间序列分析。BG算法通过不平稳结点检验将一定时间长度的灾情资料进行时间序列切分,使得变异系数的推算能在一平稳时间序列里进行。而且发现以BG算法的期望偏差作为变异系数比用标准差要合理,因为偏差体现的就是前后两个时间序列的数值差异,整体样本的标准差却不能表现出时间序列数值的变异性。
鉴于上述原因,北京地区冰雹灾害风险区划的风险评估方程建立在概率、损失及变异性的基础上。这充分体现了灾害的损失量在风险值计算中的作用,还考虑到一定时间序列下冰雹灾害灾情的变异情况。对在灾害损失评估基础上的风险区划,提出了依据不同损失系数下的雹灾发生频次,来确定一个地区的平均风险状况,以平均风险来建立风险区划的风险等级标准。最终的风险区划结果显示降雹频次大的地区不一定就是高风险区域,雹灾风险大小与地表承灾体的分布状况密切相关。
1 资料与方法 1.1 资料来源本研究选用的资料及数据包括北京地区近30年 (1980—2009年) 的雹灾历史灾情数据、北京地区基础地理信息数据及部分社会经济数据。雹灾历史灾情资料来源于北京市人工影响天气办公室收集、整理的北京市各乡、镇、村单位上报的各地方遭受历次冰雹灾害损失情况汇报资料及北京市民政局提供的部分雹灾灾情数据,此类灾害损失资料包括各次雹灾的受灾情况、受灾面积、受灾人口、经济损失等内容。为了使评估结果不受物价因素的影响,研究选用统计年鉴 (http://www.stats.gov.cn/) 提供的1980—2009年物价指数将不同年份的直接经济损失修正到2009年的物价水平。风险区划模型计算及区划图的绘制选用北京市测绘局2006年提供的1:5万比例尺的北京市基础地理信息数据。
1.2 风险评估方程评估的雹灾历史灾情资料,资料信息量比较全,可为风险评估提供较为充足的灾害损失信息,甚至是风险信息。参照文献[6]的风险评估方程并结合灾情资料,这里将方程进一步实用化为
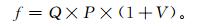
|
(1) |
式 (1) 中,P为灾害出现概率,Q为造成的损失量,V为变异系数。
风险评估方程的应用首先要依托以历史灾情为基础的损失评估,评估方程可理解为灾害风险值实际上等同于某一时间范围内所有雹灾的损失量总和,当然这个损失量是对应风险大小的损失量,并不是严格意义上的损失量。雹灾的损失量由损失评估模型根据历史灾情信息评估及转换得出。那么,以灾害事件的损失评估模型为驱动的风险评估方程为
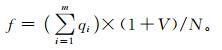
|
(2) |
式 (2) 中,m为统计资料中某一时段内的雹灾次数,qi为各次雹灾的灾损系数 (灾损评估结果),N为统计年数。这样将风险值计算简单地转化为雹灾的损失系数的统计及转换。损失评估的方法较多,主要有灾度法、圆弧法、灰色聚类及灰色关联等多种方法[2]。要从历史灾害损失数据中体现风险状况,损失评估方法还应满足一些条件:首先,灾损评估模型能客观计算出量化的损失系数值,该值能按照损失量的大小合理地归一化并完成风险数值变换;其次,灾损评估模型能处理多维灾情数据,因为一般的灾损资料至少包含有3种以上的损失情况。相对而言,圆弧法或灾度法主要依靠人员伤亡及经济损失两种情况进行评估,不满足上面条件,灰色关联模型则不受这些条件的限制。
1.3 灰色关联模型灰色关联模型的计算原则是针对不同灾情,计算其灾情——指标转换函数值序列的灰色关联度,然后通过比较关联度数值来分析、比较灾情的轻重及差异。有关灰色关联模型的应用较多,具体模型方法请参考文献[15-16]。
灰色关联模型的关联度r0i越大,它所对应的该次灾情就重,反之越轻,这可以反映出不同灾害事件之间灾情的轻重程度。关联度的理论最大值r0i_max=1,最小值r0i_min=1/3。要将关联度表示的灾情轻重转换为能体现灾害风险大小的损失系数,需要在关联度值的基础上做高斯函数变换,灾损系数
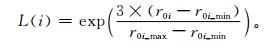
|
(3) |
这样计算出的灾损系数L(i) 能直接用于风险评估方程。对于变异系数的计算则宜采用关联度的归一化值。
1.4 变异系数的BG算法变异系数的计算采用以历史灾情资料为总体样本的时间序列分析来完成,该时间序列的数值分析以各次雹灾的灾损评估系数为基础。这里引用BG算法来测算统计时段内雹灾的灾损变异系数。BG算法主要是用t-检验来量化前后时间序列两部分数值的差异及突变检验,满足雹灾资料的时间序列分析要求。具体算法过程包括:
对统计年限范围内所有雹灾事件所构成灾损的时间序列Q(t),从左到右分别计算i年前后所有灾损系数 (灰色关联度归一化值) 的平均值u1(i) 和u2(i) 及标准偏差S1(i) 和S2(i),则i年的合并偏差SD(i) 为
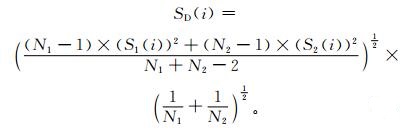
|
(4) |
式 (4) 中,N1,N2为i年前后的灾害次数。合并偏差的期望值E(SD) 可作为变异系数。
用t-检验的统计值T(i) 来量化表示i年为结点的前后两部分灾损系数均值的差异,
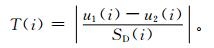
|
(5) |
对Q(t) 中的每一个点重复上述计算过程得到与Q(t) 一一对应的检验统计值序列T(t),T(t) 越大表示该年前后两部分的平均值相差越大。
然后通过计算T(t) 中的最大值Tmax的统计显著性P(Tmax) 来检验T(t) 处前后时间序列的平稳性差异,P(Tmax) 表示在随机过程中取到T值不大于Tmax的概率。P(Tmax) 可近似表示为
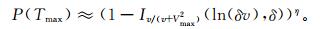
|
(6) |
式 (6) 中的参数由蒙特卡洛模拟,并满足30年等较短时间序列的计算要求,那么η=4.19lnN-3.54,δ=0.4,N是时间序列Q(t) 的长度,v=N-2,Ix(a, b) 为正则不完全β函数,在Matlab中可由程序函数Betainc[x, a, b]计算得到。
设定临近值P0(可取0.5~0.95),如果P(Vmax)≤P0,说明该时间序列均值比较稳定,变异系数可取整个时间序列的合并偏差期望,否则取后一个时段的合并偏差期望。
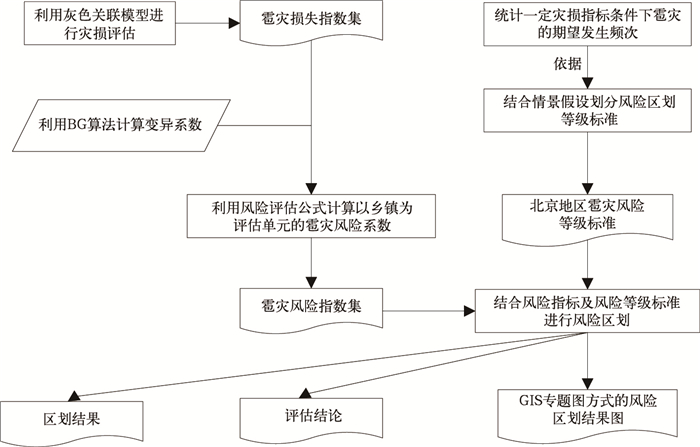
2 评估实例应用图 1为北京地区冰雹灾害风险区划的数据处理及分析的实例应用流程。具体风险区划步骤及处理过程包括:
|
|
| 图 1. 北京地区冰雹灾害风险区划技术流程图 Fig 1. The technique flow chart of hail disaster zoning in Beijing | |
① 灰色关联的灾损评估。
北京地区冰雹灾害风险区划选用北京地区各乡镇收集上报的最近30年 (1980—2009年) 的冰雹灾情数据。根据冰雹灾情特征及资料的完整程度,选用受灾人口、受灾面积及直接经济损失作为冰雹灰色关联评估模型的评估指标,并设定如表 1所示的各指标相对应的灾情转换函数。
|
|
表 1 雹灾灰色关联指标灾情转换函数 Table 1 The conversion functions of gray correlation index for hail disaster |
灾损评估首先从雹灾的历史灾情资料中选取各次雹灾的直接经济损失、受灾人口及受灾面积为评估指标,用灰色关联模型计算关联度,其归一化值及高斯函数变换值可作为灾损系数加以利用。表 2为部分数据的处理结果。灰色关联度的取值越高其灾情就越严重,为了满足评估的要求及体现风险的物理意义,这里对关联度值分别做了归一化处理及高斯变换,归一化结果主要用于灾损的时间序列分析,而高斯变换则是灾损到风险的一个转换过程,它说明了风险的递增与灾损的增加呈指数增长关系。
|
|
表 2 利用灰色关联模型的部分雹灾损失评估结果 Table 2 The partial result of loss evaluating by Gray-correlation Model |
② 基于BG算法的变异系数计算。
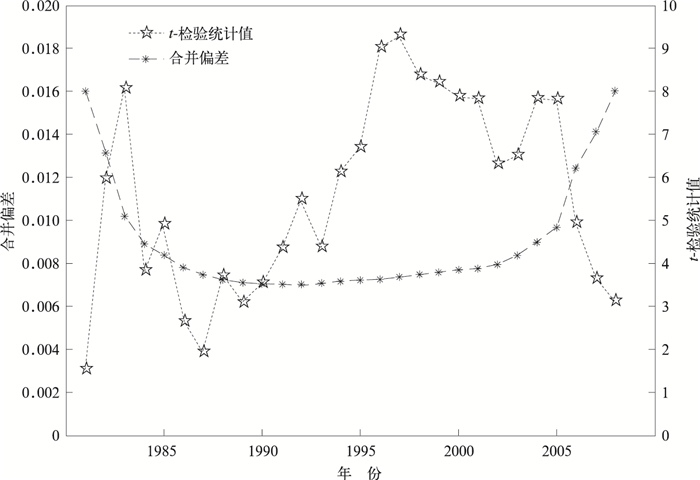
对历史灾情数据以年为单位进行时间序列分析。对于30年 (1980—2009年) 的资料,BG算法计算过程中产生了29个结点 (1981—2008年),各结点前后时间序列的合并偏差及t-检验统计值T(i) 如图 2所示。T(i) 越大说明前后时间序列的均值差异越大,从图 2中可见1997年结点的T(i) 值最大,Tmax=9.290773,而且1997年前冰雹灾情的偏差系数数值呈下降趋势,而1997年之后呈上升趋势。对1997年前后雹灾风险的平稳性进行检验,计算统计显著性P(Tmax),设定P0=0.7。
|
|
| 图 2. 采用BG算法的时间序列分析结果 Fig 2. The time series analysis result by the BG algorithm | |
检验参数Q(t) 的时间长度,
N=29,
η=4.19lnN-3.54=2.5874,
v=N-2=27,
v/(v+Tmax2)≈0.238257,
δ=0.4,那么
Iv/(v+Tmax2)(η δ, δ)=
I0.238257(10.8, 0.4)=0.096883,
由式 (6) 得,P(Tmax)=0.76823,P(Tmax)>P0,这表明1997年是个不平稳结点。根据时间序列分析的要求,北京地区雹灾的灾情时序数值在1997年结点前后分属两个平稳性不一样的时间序列。按照就近原则,变异系数的计算用1997年以后的时间序列数据,1997年以后各结点合并偏差期望E(SD) 为0.013,即为北京地区雹灾损失风险的变异系数值。
③ 结合灾损评估结果的雹灾频次统计分析。
雹灾频次统计在灾损系数计算结果 (关联度的归一化值) 的基础上完成。统计样本为北京地区近30年来发生的2848点次雹灾灾情及损失评估结果,这个样本数量基本上能够反映出北京地区冰雹灾害的总体风险状况及真实灾损特征,不需要如处理小样本事件那样对样本进行信息扩散处理,可直接用样本作频次统计。由于灾损系数取值越大灾情越严重,可按照直方图统计方式,将灾损系数在0~1范围内划分为10个等间距为0.1的数值区间 (表 3),然后统计每个区间内雹灾年均发生频次,10个区间的离散集合为
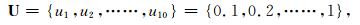
|
|
|
表 3 北京地区雹灾发生频次统计结果 Table 3 The statistics result of hail occurring frequency in Beijing |
利用灾损评估结果,统计灾损系数归一化值在0~0.1, 0.1~0.2, ……, 0.9~1区间的雹灾年均发生频次,频次以集合F={f(1), f(2), ……, f(10)}表示,结果如表 3。
④ 风险等级标准划分。
从上面的统计结果来看,北京地区平均出现归一化灾损系数为0.8以上的较严重雹灾的期望频次达到1.03点次/年,出现0.5以上雹灾的期望频次就有13.5点次/年之多,可见北京地区雹灾导致的损失及影响比较大。基于上述雹灾频次的统计,结合风险评估方程式 (1)、式 (2),可得出北京地区雹灾的平均风险值。按照表 3的结果,利用风险评估方程及灾损方程 (3),计算北京地区近30年来的地均 (单位:km2) 风险值期望,即为平均风险

|
(7) |
表 4的灾损系数是归一化的,可直接使用,L(1)~L(10) 的灾损系数取表 3中数值区间的中值,N=30,同时根据地理信息数据北京地区总面积S=16370 km2。这样风险等级标准的划分可在R′值的基础上建立,具体划分如表 4所示。
|
|
表 4 北京地区冰雹灾害风险等级划分标准 Table 4 The risk zoning standard of hail disaster in Beijing |
将极高风险区域的等级标准定为北京地区平均风险值R′的5倍及以上,高风险则是平均风险的2.5倍以上。从情景假设来看,该划分等级标准合理,具有一定的可释性及物理意义。
⑤ 北京地区冰雹灾害风险区划结果。
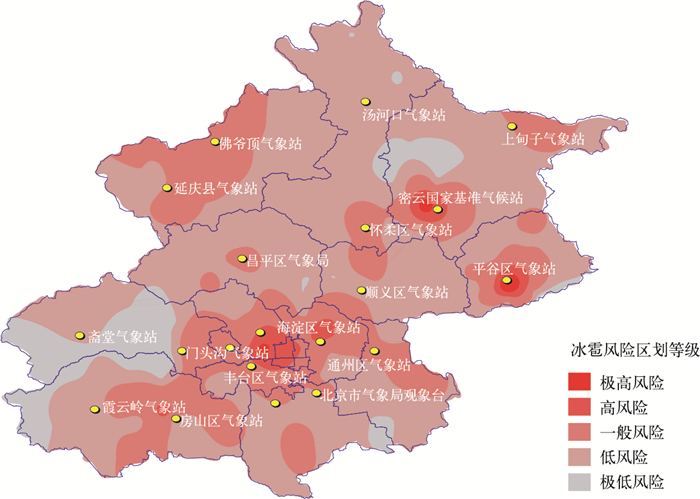
应用风险评估方程逐次计算各个乡镇历次雹灾所表现的风险值,然后以乡镇为单位计算风险系数,统计出各乡镇的地均风险值,将该值以乡镇地理质点为中心插值到北京市图幅范围内,并利用风险等级标准 (表 4) 划分风险等级区域,得到北京地区冰雹灾害风险区划图 (图 3)。
|
|
| 图 3. 北京地区冰雹灾害风险区划结果图 Fig 3. The map of the hail risk zoning status in Beijing | |
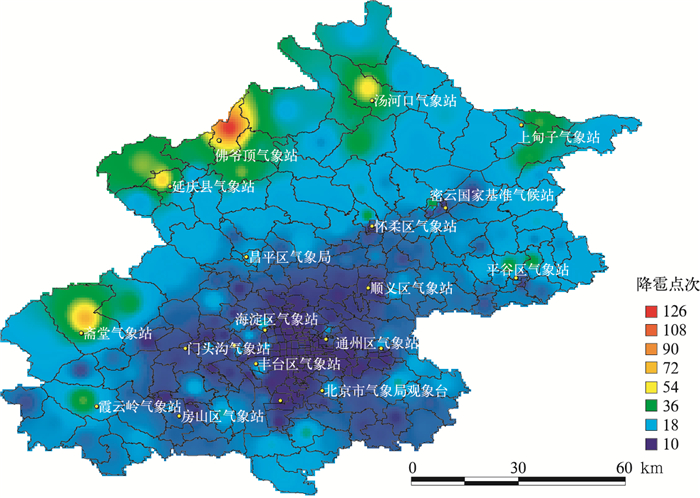
图 4为北京地区冰雹灾害发生次数分布图。由图 4可见,北京地区的降雹主要分布在北、西北及东北部山区及山前迎风坡地带,平原地区的降雹次数相对较少,这符合冰雹分布的自然特征。图 3的风险评估结果则显示,北部山区除几个降雹频次极大的地区,雹灾风险相对较高外,其他地区的风险等级均处于中等及以下风险水平,而北京市城市中心地区、密云及平谷等人口分布稠密的平原地区成为北京地区雹灾的高风险区域,这说明雹灾的风险是致灾因子和承灾体相互作用造成的。考虑承灾体的物理暴露性及可引发灾害损失的严重程度,降雹分布次数多的地区,它的灾害风险不一定大。尽管北京平原地区的降雹频次与山区相比是个低值区域,但北京的城市中心地区及部分县城是人口、经济的密集分布区,风险的物理暴露性大,暴露的承灾体种类多、数量大、价值高,形成一个较为脆弱的孕灾环境。这一评估结果与扈海波、吴焕萍等在北京奥运会期间气象灾害风险评估中应用GIS技术结合北京地区冰雹的致灾因子危险性、脆弱性、易损性及敏感性所得出的评估结论基本类似[17-21]。
|
|
| 图 4. 1980—2009年北京地区降雹点次分布图 Fig 4. The map of hail frequency distribution in Beijing from 1980 to 2009 | |
3 结论
为了得出北京地区冰雹灾害风险区划,首先利用1980年以来的历史灾情资料做了历次灾害事件的定量化损失评估;然后在损失评估的基础上完成30年时间长度的雹灾灾情时间序列分析,确定风险变异系数;进行类似直方图统计的雹灾频次分析,并根据统计结果确定风险区划等级标准;最后依据风险评估方程核算北京地区各乡镇的雹灾风险值,结合等级标准得出风险区划。由于采用了较多的历史灾情数据做样本,得到的评估及区划结果基本符合北京地区冰雹灾害的真实风险情况。总体情况及过程可总结如下:
1) 灰色关联模型计算出的关联度大小与灾情的轻重一致,为了满足区划目的,表现历史灾情信息所反映的实际风险状况,将关联度进行均一化及高斯变换两种处理,用于不同的应用目的和要求。均一化值主要用于变异系数的计算及频次统计分析,高斯变换结果值则用于风险计算。高斯变换在风险计算中起数值放大的作用,一般认为灾损量越大,所表现的风险呈指数级数增长而不是线性增加。
2) 利用BG算法对30年来的灾情资料作时间序列的平稳性分析,发现t-检验统计值在1997年出现极大值,1997年前后冰雹灾情的偏差系数数值呈现不同的下降及上升趋势。对1997年结点的统计显著性检验结果表明其显著性大于临近值,说明1997年是不平稳结点。据此将30年来的灾情数据以1997年为切割点划分为前后两个时间序列,用1997年以后的时间序列的期望偏差作为变异系数,系数反映北京地区雹灾灾情变异情况。
3) 将灾损评估结果作了0~1数值范围内10个等间距的形式上类似直方图统计方法的雹灾频次统计,统计结果反映出北京地区的雹灾灾情比较严重。频次统计结果用于推算北京地区平均风险状况,平均风险状况用地均风险期望值表示,该值可作为冰雹灾害风险区划等级标准的划分依据。等级标准从情景假设来看,具有相当的物理意义及可解释性。
4) 结合灾损评估结果、变异系数结果,用风险评估方程计算北京地区各个乡镇的风险值,计算结果按风险区划等级标准进行风险区域划分。从区划结果看,尽管北京地区北、西北及东北部山区及山前迎风坡地带的降雹频次较大,但这些地区人口相对稀疏,其引发的雹灾风险并不大。而平原地区由于雹灾的物理暴露性较强,承灾体的种类、数量及价值相对较大,所导致冰雹灾害的损失风险也大。因此,位于平原地带的北京市城市中心地区、密云县城及平谷区等人口稠密地区反而是雹灾的高风险区域。
| [1] | 扈海波, 董鹏捷, 熊亚军, 等. 北京奥运期间冰雹灾害风险评估. 气象, 2008, 34, (12): 84–89. |
| [2] | 马宗晋, 李闵峰. 自然灾害评估、灾度和对策//中国减轻自然灾害研究. 北京: 中国科学技术出版社, 1990. |
| [3] | 张会, 张继权, 韩俊山. 基于GIS技术的洪涝灾害风险评估与区划研究——以辽河中下游地区为例. 自然灾害学报, 2005, 14, (6): 141–146. |
| [4] | 马明, 吕伟涛, 张义军, 等. 1997—2006年我国雷电灾情特征. 应用气象学报, 2008, 19, (4): 393–400. DOI:10.11898/1001-7313.20080402 |
| [5] | 宫德吉, 郝慕玲. 白灾成灾综合指数的研究. 应用气象学报, 1998, 9, (1): 119–123. |
| [6] | Smith K. Environmental Hazards: Assessing Risk and Reducing Disaster (2nd edition). New York: Routledge, 1996. |
| [7] | 黄崇福. 自然灾害风险评价理论与实践. 北京: 科学出版社, 2005. |
| [8] | Huang Chongfu. Two models to assess fuzzy risk of natural disaster in China. Journal of Fuzzy Logic and Intelligent Systems, 1997, 14, (6): 141–146. |
| [9] | 杜晓燕, 黄岁樑, 赵庆香. 基于信息扩散理论的天津旱涝灾害危险性评估. 灾害学, 2009, 24, (1): 22–25. |
| [10] | 李世奎, 霍治国, 王素艳, 等. 农业气象灾害风险评估体系及模型研究. 自然灾害学报, 2004, 13, (1): 77–87. |
| [11] | 蒋卫国, 盛绍学, 朱晓华, 等. 区域洪水灾害风险格局演变分析——以马来西亚吉兰丹州为例. 地理研究, 2008, 27, (3): 502–508. |
| [12] | 倪化勇, 刘希林. 自然灾害发生时间序列的分形特征及R/S分析. 自然灾害学报, 2005, 14, (6): 37–41. |
| [13] | 高庆华, 马宗晋, 张业成, 等. 自然灾害评估. 北京: 气象出版社, 2007. |
| [14] | Pedro B G, Plamen C I, Luis N A, et al. Scale invariance in nonstationarity of human heart rate. Physical Review Letters, 2001, 87, (16): 168105. DOI:10.1103/PhysRevLett.87.168105 |
| [15] | 刘伟东, 扈海波, 程丛兰, 等. 灰色关联度方法在大风和暴雨灾害损失评估中的应用. 气象科技, 2007, 35, (4): 563–566. |
| [16] | 杨仕升. 自然灾害不同灾情的比较方法探讨. 灾害学, 1996, 11, (4): 35–38. |
| [17] | 扈海波, 熊亚军, 董鹏捷, 等. 北京奥运期间 (6—9月) 气象灾害风险评估. 北京: 气象出版社, 2009. |
| [18] | 扈海波, 王迎春, 熊亚军. 基于层次分析模型的雷电灾害风险评估. 自然灾害学报, 2010, 19, (1): 104–109. |
| [19] | 扈海波, 王迎春, 刘伟东. 气象灾害事件的数学形态学特征及空间表现. 应用气象学报, 2007, 18, (6): 802–809. DOI:10.11898/1001-7313.200706122 |
| [20] | 扈海波, 熊亚军, 张姝丽. 基于城市交通脆弱性核算的大雾灾害风险评估. 应用气象学报, 2010, 21, (6): 732–738. DOI:10.11898/1001-7313.20100610 |
| [21] | 吴焕萍, 罗兵, 王维国, 等. GIS技术在决策气象服务系统建设中的应用. 应用气象学报, 2008, 19, (3): 380–384. DOI:10.11898/1001-7313.20080316 |
 2011, 22 (5): 612-620
2011, 22 (5): 612-620