2. 南京信息工程大学大气科学学院, 南京 210044
2. College of Atmospheric Science, Nanjing University of Information Science & Technology, Nanjing 210044
长江中下游地形平坦,人口密集,素称“鱼米之乡”,是我国经济较发达的地区之一。但受东亚季风的影响,该地区又是我国洪灾多发区域之一,几乎每年都会遭到不同程度的洪涝侵袭。洪灾严重制约着该地区经济社会的可持续发展,因此,已经有大量研究集中于洪灾机理的研究[1-5]。但对于长江中下游地区洪涝风险的评估还相对欠缺,而掌握洪涝的风险性对制定相应的防灾、抗灾政策具有更为重要的现实意义。
洪涝风险性评估目的是评估不同程度洪涝发生的可能性,即概率密度分布。当有足够多的历史资料,采用基于大数理论的传统概率方法能得到比较精确的评估结果。但洪涝历史灾情往往资料短缺,达不到传统概率风险评估所需30个以上样本的要求,因此,利用传统概率论方法分析所得的结果必然存在较大的不确定性,有时甚至会与实际相差甚远。模糊数学中的信息扩散理论则解决了样本缺失的问题,认为存在着一个适当的扩散函数,可以将传统的观测样本点集值化,以弥补资料不足带来的缺陷,达到提高精度的目的[6]。
信息扩散理论是黄崇福等[6]系统提出的,一些学者也对该理论进行了大量的探讨和研究,使理论模型不断完善。刘立新等[7]对信息扩散方法进行过修正,并通过计算机仿真证实了修正后模型提高了估计精度。王新洲等[8-9]提出了最优窗宽的理论和算法以及最优信息扩散估计的概念。李梅等[10]针对信息扩散估计的过扩散和欠扩散问题,在分析择近窗宽法和最优窗宽法的基础上,结合二者的优点,又提出了一种确定扩散窗宽的多目标综合优化方法。
到目前为止,该方法在自然灾害的风险评价领域已得到了广泛应用。黄崇福等[11]针对湖南农业旱灾、水灾的数据资料时间序列短、数量少的特点,选择信息扩散方法进行概率密度估计,得出了湖南农业受灾风险,并将所得结果制成专题图,直观展示了风险分布及随灾害程度增加风险的空间变化趋势。近年来,刘引鸽等[12]探讨了以灾害样本为集值的基于信息扩散的模糊数学理论模型的气象灾害风险评价方法,对西北农业旱灾进行了风险评价实例分析。对比分析表明,西北农业受旱指数、成灾指数发生灾损概率风险估计值与实际较吻合。杜晓燕等[13]采用信息扩散理论的评估模型,以天津22年的旱涝指数为样本,对天津旱涝危险性进行评估,给出了天津旱涝指数概率密度曲线及不同程度旱涝危害发生的可能性。刘家福等[14]根据我国1988—2007年发生的洪水灾害次数、人口死亡数和经济损失3个统计指标,分别对各项指标运用信息扩散理论定量评价了我国洪水灾害风险。这些实践结果均表明:信息扩散模型对信息量不足的自然灾害进行风险评估是可行的。
不过,大多数评估主要针对农业受灾、洪灾造成的各单项损失或者旱涝指数而进行。但洪涝所造成的危害不仅仅局限于某一方面,它涉及到人类、社会以及经济等各个方面。而旱涝指数仅能反映区域旱涝的风险水平,并不能全面揭示受灾的严重程度,有一定局限性。以往研究较好地分析了区域单个指标风险性,但所得到的评估结果往往比较分散,无法权衡区域整体受害程度。为了全面反映区域洪灾的严重程度并体现区域灾情差异,本文首先基于现有的洪涝灾情资料建立一个综合反映地区洪涝受灾程度的灾情指数,然后运用信息扩散评估模型对长江中下游地区进行洪涝风险分析,这样所得的各省洪涝风险结果就一目了然,可为区域防灾、减灾提供一个具有参考价值的理论基础。
1 资料与方法 1.1 资料根据国家减灾中心灾害信息部正式公布的灾情实况,中国科学院减灾中心工作项目汇集的洪涝灾情数据,包括2000—2008年全国各省每次洪涝灾害发生的起止时间、受灾县数、农作物受灾面积、成灾面积、受灾人口、死亡人数、倒塌房屋、直接经济损失。
民政部提供的2000—2008年全国各省每年的洪涝灾情汇总数据,包括农作物受灾面积、成灾面积、受灾人口、死亡人数、倒塌房屋、直接经济损失。
1.2 信息扩散理论风险估算模型信息扩散是一种有效处理小样本的方法[15],它为了弥补信息不足而考虑优化利用样本的模糊信息,从而对样本进行集值化。该方法可以将只有一个观测值的样本,变成一个模糊集,即将单值样本变成集值样本[16]。
本文在风险分析时主要运用刘立新[16]所介绍的时间不完备数据基础上的风险估算模型。信息扩散方式很多,但是目前比较成熟的是正态扩散模型。
设灾害指数论域为
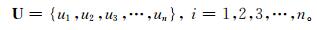
|
(1) |
设灾害指数样本集合为
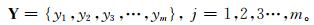
|
(2) |
对灾害指数的第j个样本yj依据式 (3) 进行扩散:
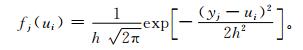
|
(3) |
式 (3) 中,h为扩散系数,可以根据样本集合中样本的最大值b、最小值a和样本个数m来确定,
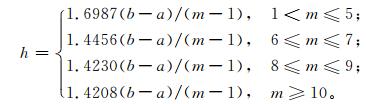
|
(4) |
令
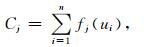
|
(5) |
相应的模糊子集的隶属函数为
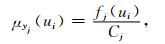
|
(6) |
称μyj(ui) 为样本yj的归一化信息分布。
对m个μyj(ui) 进行处理,就可以得到风险估算结果。
令
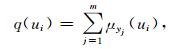
|
(7) |
再令
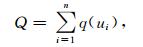
|
(8) |
则
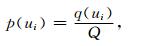
|
(9) |
就是样本落在ui处的频率值,可作为概率的估计值。
由此超越概率值,即单位时间内受灾指数达到或超过ui的概率值也可由式 (10) 计算得出:
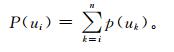
|
(10) |
参照马宗晋等[17]、于庆东等[18]、杨仕升[19]的自然灾害绝对灾情单指标分级标准,并根据我国灾情统计数据特点以及衡量洪涝灾情的重要性指标[20],本文选择了由民政部以及中国科学院减灾中心工作汇编的2000—2008年长江中下游六省每年洪涝灾情数据中所包含的受灾人口、农作物受灾面积和直接经济损失3项作为洪涝灾害指标 (其他灾情统计项缺失值太多,无法列入指标计算),将洪涝灾害分为巨灾、大灾、中灾、小灾、微灾5个等级 (表 1)。
|
|
表 1 洪涝灾害等级和单项指标分级标准 Table 1 Flood grades and standard of classification for individual index |
由于各单项指标具有不同的量纲,不能直接进行比较,同时也为了使不同指标划分洪涝灾害等级标准统一,必须对各指标进行无量纲化,本文引入转换函数[18]对表 1的分级标准进行等价变化。各单项指标的转换函数如下:
受灾人口:
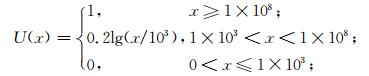
|
(11) |
x单位:人。
农作物受灾面积:
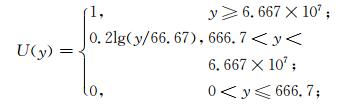
|
(12) |
y单位:hm2。
直接经济损失:
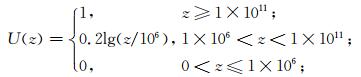
|
(13) |
z单位:元。
经用转化函数处理后,单项指标转换函数对应的洪涝灾害等级如表 2所示。
|
|
表 2 洪涝灾害等级与单项转换函数的关系 Table 2 The relationship between individual conversion function and flood grades |
2.2 洪涝综合灾情指数定量化
通过上述转换函数,各个单项指标转变为量纲为1,从而使各指标间有了一定的可比性。但对于不同区域进行单指标的比较并不能集中反映区域整体受灾差异。因此,为了体现区域间洪涝受灾的这种整体差异,有必要以各指标为准,构建一个综合洪涝灾情指标。之前有许多学者对综合指标进行过探讨和研究[18-21],但目前还没有形成完全统一的标准。这里在计算洪涝综合灾情指数时,主要参照灰色关联分析方法[19]。
设参考序列
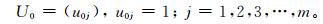
|
(14) |
表示灾害的各单项指标的转换函数值均为1,属于标准巨灾;比较序列
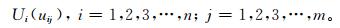
|
(15) |
比较各次灾害的转换函数值序列Ui与参考序列U0的关联程度,就可计算出关联度。
模仿灰色关联系数的定义方法[22],引入比较序列与参考序列各项指标的关联系数为
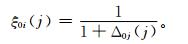
|
(16) |
式 (16) 中,Δ0j(j)=|U0(u0j)-Ui(uij)|, i=1, 2, 3, …, n; j=1, 2, 3, …, m,表示比较序列Ui的第j项指标与参考序列U0的绝对差值。绝对差值越大,说明该单项指标与参考序列中同项指标的距离就越大,关联系数就越小;反之,绝对差值越小,关联系数就越大。由于Δ0j(j) 的取值区间为[0, 1],因此,关联系数的取值区间为[0.5,1]。
从式 (16) 计算得到的比较序列与参考序列各项指标的关联系数,但有m个指标,因此采用等权处理的平均值法,将每个比较序列的各项指标关联系数体现在一个值上,此值则为关联度:
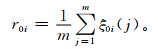
|
(17) |
关联度是比较序列与参考序列各项指标的关联系数总和的平均值,它集中反映了比较序列与参考序列的关联程度。很显然r0i的值域为[0.5,1]。关联度越大,灾情越严重;反之,关联度越小,灾情越轻。关联度的大小可以反映灾情的轻重,因此可以通过其取值来划分洪涝灾害等级 (表 3)。
|
|
表 3 关联度与洪涝灾害等级的对应关系 Table 3 The corresponding relationship between the correlation degree and flood grades |
将关联度从大到小进行排序,便可得到关联度顺序。而关联度顺序反映了灾情由重到轻的排序,由此可得到灾情重轻的比较关系。因此在研究过程中定义洪涝综合灾情指数等于关联系数。
本文进行风险评估时以2000—2008年长江中下游各省年洪涝受灾资料为依据,运用上述指数定量化的方法计算出各省每年的洪涝综合灾情指数,分析其结果,可以看出各省每年受灾程度的差异 (表 4)。
|
|
表 4 各省每年的洪涝综合灾情指数与受灾等级划分 Table 4 The synthetic disaster index and afflicted grades for flood disaster of each province |
由表 4可以看到,进入21世纪后,长江中下游地区的洪涝综合灾情指数总体维持在0.6~0.9的范围,灾害等级主要集中于大灾、中灾以及小灾。湖北、安徽发生大灾的次数最为频繁,9年中,3年遭遇大灾的侵袭;其次为湖南。江西洪涝综合受灾指数始终维持于0.7~0.8,中灾频发。江苏、浙江发生的洪涝等级主要为中灾和小灾,灾害损失相对较轻。
由以上分析可以看出,洪涝综合灾情指数简明地体现了各省每年灾害损失的轻重程度。为了证实该指数的可行性,计算了该指数与实际各单项指标的相关系数,其中与受灾面积的相关系数达0.86,与受灾人口的相关系数为0.91,与直接经济损失的相关系数为0.82,均通过0.01显著性水平检验,再次证明了该洪涝综合灾情指数的合理性,分析该指数就能够较好反映各省每年受灾差异,是一个能够综合权衡区域受灾的指标。
3 长江中下游洪涝风险评估在计算获得了长江中下游近9年的洪涝综合灾情指数后,便可运用信息扩散理论进行各省洪涝风险性估算。
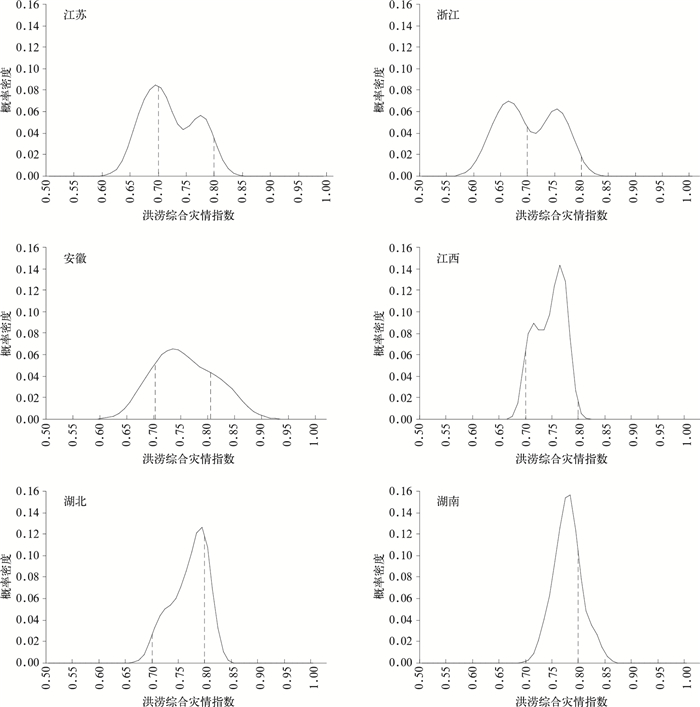
洪涝综合灾情指数定量化分析过程中已经得知,其值域为[0.5,1]。因此,为了提高计算精确度,洪涝综合灾情指数的论域取U={u1, u2, u3, …, u51}={0.50, 0.51, 0.52, …, 1},各省综合灾情指数Y={y1, y2, y3, …, y9}(如表 4所示)。按照信息扩散理论的风险模型进行估算,由于控制点选取较密集,其计算结果就可近似看做连续型的概率密度函数。于是根据估算模型就得出了每个省份在各灾情区间上的概率值 (图 1)。
|
|
| 图 1. 长江中下游地区洪涝综合灾情指数概率密度曲线 Fig 1. The probability density curve of synthetic disaster index in the mid-lower Reaches of the Yangtze | |
从图 1可以看出,长江中下游每个省在各受灾论域上发生概率的整体形势以及省际差异。全区洪涝综合灾情指数在0.7~0.8的值域上所占比例最大,主要以中灾为主,发生巨灾的可能性较小。安徽发生大灾的风险性水平最高,其次为湖北、湖南以及江苏。江西为中灾频发省,概率曲线几乎覆盖了0.7~0.8整个区间。同时,湖北、湖南中灾发生也十分频繁。浙江小灾发生的频率最高,灾情相对偏小。
再根据式 (10),就可估算出每个省份各灾级洪涝发生的风险性水平 (表 5)。
|
|
表 5 长江中下游六省各灾级洪涝发生的风险水平 Table 5 The risk level of six provinces in the mid-lower Reaches of the Yangtze |
由表 5可知,长江中下游六省各种灾级的洪涝风险水平有明显差异。整体而言,该区域发生中灾的风险性水平最大 (除浙江省),与上述概率分布曲线相对应。安徽有发生巨灾的可能,其估计值达0.004,说明该省约250年可能遭遇一次巨灾的侵袭。大灾在安徽、湖北、湖南出现的可能性较大,分别约每4年、4.5年以及4.7年遇到一次。江苏、浙江则分别在间隔19年、42年可能会遇到大灾,江西发生大灾则百年一遇。中灾在每个省发生都极为频繁,江西尤为突出,基本为年遇型。湖北、湖南、安徽以及江苏也基本上不到两年就会遭遇一次中灾。小灾则以浙江最为集中,其次为江苏和安徽。总体上看,湖北、湖南、江西洪涝发生大灾、中灾的概率最集中,灾情最为严重,其次为安徽;而江苏中灾和大灾的发生概率也超过了0.6,灾情也相对较重。在所有的灾级中,浙江小灾比例最大,因此洪涝受灾与其他省份相比最轻。
为了验证该评估模型所得估算结果的准确性,表 6给出了2000—2008长江中下游每个省各灾级洪涝发生频率的实际统计资料。经对比分析发现,各省各灾级灾情发生频率的估算结果与实际统计结果十分吻合,计算二者的相关系数达0.99。经显著性检验,超过0.01显著性水平,再次证明该模型所得的评估结果比较有效。
|
|
表 6 长江中下游六省2000—2008年各级洪涝灾害实际发生的频率 Table 6 The flooding frequency of each province along the mid-lower Reaches of the Yangtze during 2000—2008 |
4 结论与讨论
本文基于长江中下游六省2000—2008年的洪涝灾情资料,以灰色关联分析法为依据建立了洪涝综合灾情指数,并基于该指数运用信息扩散理论对该区域的洪涝风险性水平进行评估,得到以下结论:
1) 运用灰色关联分析方法建立的洪涝综合灾情指数,在风险评估中是能较集中、全面反映区域整体受灾情况的一个合适的指数。
2) 基于综合灾情指数运用信息扩散理论对长江中下游洪涝灾害评估,得到了各省洪涝受灾严重程度的概率分布,反映出了洪涝灾损的省际差异。从总体上看,浙江受灾最轻,其灾害等级在小灾、中灾比较集中,而其他各省在大灾、中灾所占的比例较大。安徽、湖北以及湖南发生大灾的可能性最大,江苏、浙江次之,江西遭遇大灾的概率相对较小。中灾在整个区域频发。
3) 运用信息扩散理论能够对不完备信息进行优化从而对各省的危险性进行评估,估算结果与实际统计值非常吻合,再次证明该模型处理小样本的可行性。
尽管以上分析结果比较理想,但样本较少,同时验证数据独立性不强,因此存在一定偏差是不可避免的。同时,本文在进行评估时只挑选了洪涝灾情数据中3个数据较完整的统计量,要使评估结果更加真实、详尽,灾情资料还需完善,综合灾情指数仍需进一步优化;此外在评估过程中所用的直接经济损失资料并没有扣除物价上涨因素,这也是一个缺陷。因此,要使灾害评估结果更符合实际灾情,今后还要对数据资料以及评估模型做更深入的分析和研究,从而为灾害评估提供更为有效的参考。
| [1] | 周自江, 宋连春, 李小泉. 1998年长江流域特大洪水的降水分析. 应用气象学报, 2000, 11, (3): 287–296. |
| [2] | 薛秋芳, 任传森, 陶诗言. 1998年长江流域洪涝的成因分析. 应用气象学报, 2001, 12, (2): 245–250. |
| [3] | 张顺利, 陶诗言, 张庆云, 等. 1998年中国暴雨洪涝灾害的气象水文特征. 应用气象学报, 2001, 12, (4): 442–457. |
| [4] | 谢安, 毛江玉, 宋焱云, 等. 长江中下游地区水汽输送的气候特征. 应用气象学报, 2002, 13, (1): 67–77. |
| [5] | 李峰, 何立富. 长江中下游地区夏季旱涝年际、年代际变化的可能成因研究. 应用气象学报, 2002, 13, (6): 718–726. |
| [6] | 黄崇福, 王家鼎. 模糊信息优化处理技术及其应用. 北京: 北京航天航空大学出版社, 1995. |
| [7] | 刘立新, 黄崇福, 史培军. 对不完备样本下风险分析方法的改进及应用——以湖南省农村种植业水灾为例. 自然灾害学报, 1998, 7, (2): 10–16. |
| [8] | 王新洲, 游扬声. 论信息扩散估计的窗宽. 测绘科学, 2001, 26, (1): 16–19. |
| [9] | 王新洲, 游扬声, 汤永净. 最优信息扩散估计理论及其应用. 地理空间信息, 2003, 1, (1): 10–21. |
| [10] | 李梅, 张洪波, 黄强, 等. 基于信息扩散估计的洪水风险分析. 中北大学学报 (自然科学版), 2007, 28, (3): 193–198. |
| [11] | 黄崇福, 刘立新, 周国贤, 等. 以历史灾情资料为依据的农业自然灾害风险评估方法. 自然灾害学报, 1998, 7, (2): 1–9. |
| [12] | 刘引鸽, 缪启龙, 高庆九. 基于信息扩散理论的气象灾害风险评价方法. 气象科学, 2005, 25, (1): 84–89. |
| [13] | 杜晓燕, 黄岁樑, 赵庆香. 基于信息扩散理论的天津旱涝灾害危险性评估. 灾害学, 2009, 24, (1): 22–25. |
| [14] | 刘家福, 梁雨华. 基于信息扩散理论的洪水灾害风险分析. 吉林师范大学学报:自然科学版, 2009, 3: 78–80. |
| [15] | Huang Chongfu. Principle of information diffusion. Fuzzy Sets and Systems, 1997, 91: 69–90. DOI:10.1016/S0165-0114(96)00257-6 |
| [16] | 刘立新. 区域水灾风险评估的理论与实践. 北京: 北京大学出版社, 2005. |
| [17] | 马宗晋, 杨华庭, 高建国, 等. 我国自然灾害的经济特征与社会发展. 科技导报, 1994, 7: 61–64. |
| [18] | 于庆东, 沈荣芳. 自然灾害绝对灾情分级模型及应用. 系统工程理论方法应用, 1995, 4, (3): 47–52. |
| [19] | 杨仕升. 自然灾害等级划分及灾情比较模型探讨. 自然灾害学报, 1997, 6, (1): 8–13. |
| [20] | 刘燕华, 李钜章, 赵跃龙. 中国近期自然灾害程度的区域特征. 地理研究, 1995, 14, (3): 14–25. |
| [21] | 冯利华. 灾害损失的定量计算. 灾害学, 1993, 8, (2): 17–19. |
| [22] | 傅立. 灰色系统理论及其应用. 北京: 科学出版社, 1992: 191–199. |
 2011, 22 (5): 604-611
2011, 22 (5): 604-611



