混合层因其较强的垂直混合使得位温、水汽等要素随高度均匀混合而得名。混合层厚度是标志大气边界层热力学和动力学特性的重要参量，也是研究来自地表污染物向大气排放的重要参数。在大气环境质量预测中，混合层厚度是重要参数之一。混合层厚度反映了污染物在垂直方向扩散的程度，也是影响大气污染物扩散的主要气象因子之一^[1]。混合层还具有明显的随时间变化特征，而不同的气象条件和天气过程也会深刻地影响混合层厚度。

利用气象探空气球所得位温、湿度、空气折射系数 (通过计算) 等垂直廓线，根据混合层内位温和湿度等要素分布较为均一的特点，利用位温、湿度和折射系数梯度来确定混合层厚度是重要方法之一^[2-5]。若将常规气象探空资料与臭氧浓度的探测资料相结合，则可以发现臭氧浓度的垂直分布与混合层的变化也有着密切的联系：在混合厚度以下，臭氧浓度垂直分布比较均匀，而在此之上，混合层向自由大气的过度区域，臭氧浓度的垂直分布有较剧烈的变化^[6]。另外，风廓线仪和气溶胶激光雷达也可以反演风或气溶胶垂直分布，以确定混合层厚度^[6]。利用经验公式和模式计算混合层厚度也是常用方法^[7-14]。

鉴于探测仪器的昂贵，特别是常规业务气象探空的时间限制 (因为常规的气象探空均在08：00(北京时，下同)，20：00左右释放)，从常规气象探空资料难以反映白天真实的边界层发展状况。因此，对混合层厚度的确定，可能更多依赖于理论上经验性的参数方法。比较典型的是干绝热法，由Holzworth^[15-16]提出, 考虑在典型的大气条件下, 夜间由于地面辐射冷却，使接近地面空气形成逆温, 呈稳定状态；白天由于太阳辐射而呈不稳定状态, 忽略平流、下沉及机械湍流影响时, 平均混合层厚度则可由清晨探空温度廓线和地面最高、最低气温而定。Nozaki^[17]则提出混合层是由热力和机械湍流共同作用的结果, 且边界层上部大气运动状况与地面气象参数间存在着相互联系和反馈作用，因此, 可用地面常规气象参数来估算平均混合层厚度。Cheng等^[18]用该方法计算了北京首都国际机场1991—1995年混合层厚度，得出该方法的平均误差为31.5%。

本文使用Nozaki方法^[17]计算了14:00的混合层厚度，并与我国7个站 (表 1) 短期的臭氧探空观测数据中气象探空数据 (分别由位温和折射系数垂直廓线确定) 所揭示的混合层厚度作对比分析，以了解经验性参数方法所确定的边界层混合层厚度在不同地区的准确性与适用性 (其中西宁1995—1996年释放探空气球的时间是10：00左右)。

表 1

表 1 龙凤山等7个站点地表覆盖状况及气象探空气球放飞时间和样本统计 Table 1 Land-cover types, delivering time of radiosonde balloons and quantities of balloons at 7 sites 地点 地表状况 位置 海拔/m 臭氧探空气球 放飞时间 总样 本量 剔除 样本量 所用 样本量 气球放飞 时间 龙凤山 森林覆盖 44°N，127°E 160 2005-04-01—05-13 21 0 21 11：00—12：00 北京 城市郊区 39°N，116°E 34 2002-01-11—01-23 2005-04-11—05-15 61 6 1 0 5 16 14：00 14：00 临安 森林覆盖 30°N，119°E 98 2001-02-21—04-11 2004-04-05—05-19 26 19 0 0 26 19 14：00 14：00 阿勒泰 平原郊区 47°N，88°E 737 2005-04-01—05-13 22 0 22 13：00—14：00 三亚 海滨郊区 18°N，109°E 6 2004-04-02—05-21 24 1 23 14：00 西宁 山地郊区 36°N，101°E 2296 1995-10-16—1996-08-03 2002-01-08—01-28 2005-04-04—05-13 46 9 22 1 0 2 45 9 20 10：00左右 13：00—14：00 13：00—14：00 腾冲 高原郊区 25°N，98°E 1655 2004-04-03—05-19 20 1 19 14：00

表 1 龙凤山等7个站点地表覆盖状况及气象探空气球放飞时间和样本统计 Table 1 Land-cover types, delivering time of radiosonde balloons and quantities of balloons at 7 sites

Nozaki^[17]认为可用地面常规气象参数来估算平均混合层厚度, 并提出如下的计算公式：

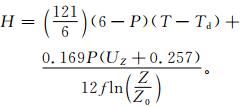
(1)

式 (1) 中，T-T_d为露点温度差 (单位：K)；P为帕斯奎尔 (Pasquill) 稳定度级别^[19]；U_Z为Z高度处 (Z=10 m) 所观测的平均风速 (单位：m/s)；Z₀为地表粗糙度；f为地转参数 (单位：s^-1)。式 (1) 中，T，T_d和P是考虑热力对流的因子，而U_Z和Z₀是考虑湍流与动力的因子。

式 (1) 中T，T_d和U_Z均可由自动气象站资料提供，P可由云量与太阳天顶角判别，因此如何选取地表粗糙度Z₀将影响混合层的计算结果。

Z₀为地表粗糙度，而下边界出现的几何长度，是对数风速廓线公式中的平均风速等于零的高度。密林以及城镇郊区的地表粗糙度实际变化范围大约在0.1~1 m之间^[20-21]。参考文献[18]对地表粗糙度的取值，考虑本文7个站点的地理位置都处于郊区或林地，地表覆盖有林地以及少数建筑物，计算混合层时对地表粗糙度的选择：夏、秋季节，Z₀=0.2 m；冬、春季节，Z₀=0.1 m^[17]。夏、秋季节与冬、春季节Z₀的差异是植被的季节变化所致，一般夏、秋季节树木茂盛，而冬、春季节树木落叶较为稀疏。

图 1是根据典型的气象探空曲线 (温度和气压所确定的位温) 来确定混合层厚度的个例。由图 1a可知，北京此时 (气球放飞时间为14：00) 混合层的厚度约为1100 m (图中虚线，H₁所指示的高度)，因为位温垂直廓线图上在1100 m左右出现较大变化，臭氧浓度和相对湿度也在此高度表现出明显变化。图 1b给出临安2001年3月5日观测的情况 (气球放飞时间为14：00)，臭氧浓度和相对湿度的垂直分布尽管有明显变化，但都很难判断混合层厚度，而从风速、风向可以看出，500 m高度处为转折点，位温垂直廓线也在500 m左右有明显变化，因此可以确定混合层厚度约为500 m。

图 1

图 1. 典型的气象探空资料位温曲线判断混合层厚度结果 (H1：混合层厚度) (a) 北京，2005年4月11日, (b) 临安，2001年3月5日 Fig 1. Typical potential temperature profiles to identify mixing layer depth (H1 denotes mixing layer depth) (a) in Beijing on 4 April 2005, (b) in Lin'an on 15 March 2001

通过位温垂直分布来确定边界层混合层厚度的方法带有一定主观性，因为位温垂直分布的变化需要目测来确定。为了克服这种主观判断带来的不确定性，本文还同时采用折射系数法来确定边界层混合层厚度。在较低对流层折射系数可以表示为^{[2, 22]}

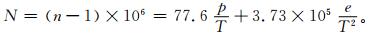
(2)

式 (2) 中，N是折射系数，n是大气折射率，p是大气压力 (单位：hPa)，T是大气温度 (单位：K)，e是水汽分压 (单位：hPa)。折射系数梯度表现出折射系数的变化程度，从而可以判断在哪一高度折射系数变化最大。考虑到N同时包括了气压、温度和水汽分压因素，所以折射系数梯度比位温较多地包含了大气垂直分布廓线的信息。设定折射系数梯度值为-5/100 m (即折射系数每100 m变化减5) 为阈值，小于该值的折射系数梯度确定为混合层厚度^[2]。

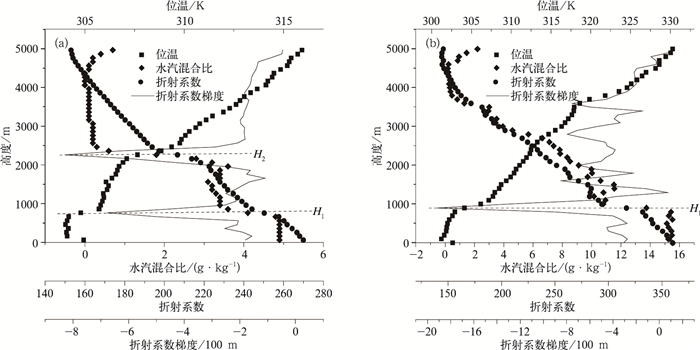
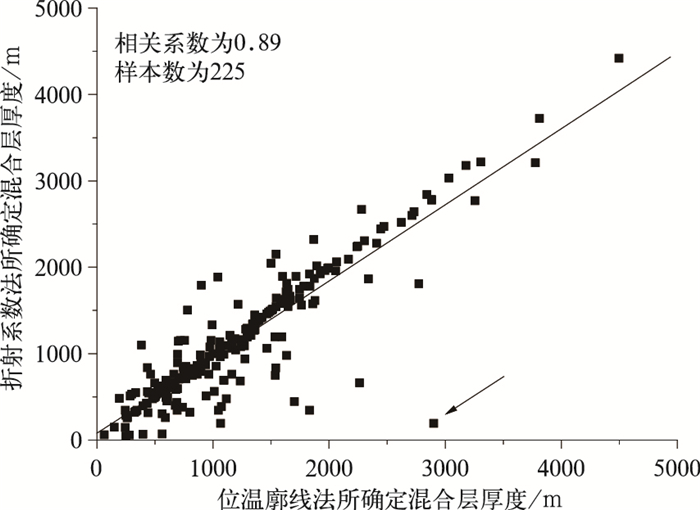
图 2是典型的折射系数和折射系数梯度以及位温和比湿垂直分布廓线。根据折射系数梯度可以明显判断出混合层的厚度，而且与位温和比湿的垂直廓线所能指示的混合层厚度非常符合。需要注意的是，有时候折射系数梯度有几个明显的极小值 (均小于阈值-5/100 m)，如图 2a所示，根据折射系数极值可以判断H₁和H₂这2个高度，此时混合层厚度应为H₁，H₂实际是残留层高度。图 3为位温廓线法与折射系数法所确定的混合层厚度的对比两者的一致性很好。但是个别点的偏离程度很大 (如图中箭头所示)，对个别点的分析见本文的讨论部分。

图 2

图 2. 典型的折射系数与折射系数梯度曲线用于确定混合层厚度 (H1：混合层厚度；H2：残留层高度) (a) 阿勒泰，2005年5月9日, (b) 三亚，2004年4月19日 Fig 2. Typical refractivity profiles to identify mixing layer depth (H1 denotes mixing layer depth; H2 denotes residual layer depth) (a) in Aletai on 9 May 2005, (b) in Sanya on 19 April 2004

图 3

图 3. 气象探空数据的位温廓线法与折射系数法所确定的混合层厚度的对比 Fig 3. Comparison of mixing layer depths determined by potential temperature and refractivity profiles, respectively

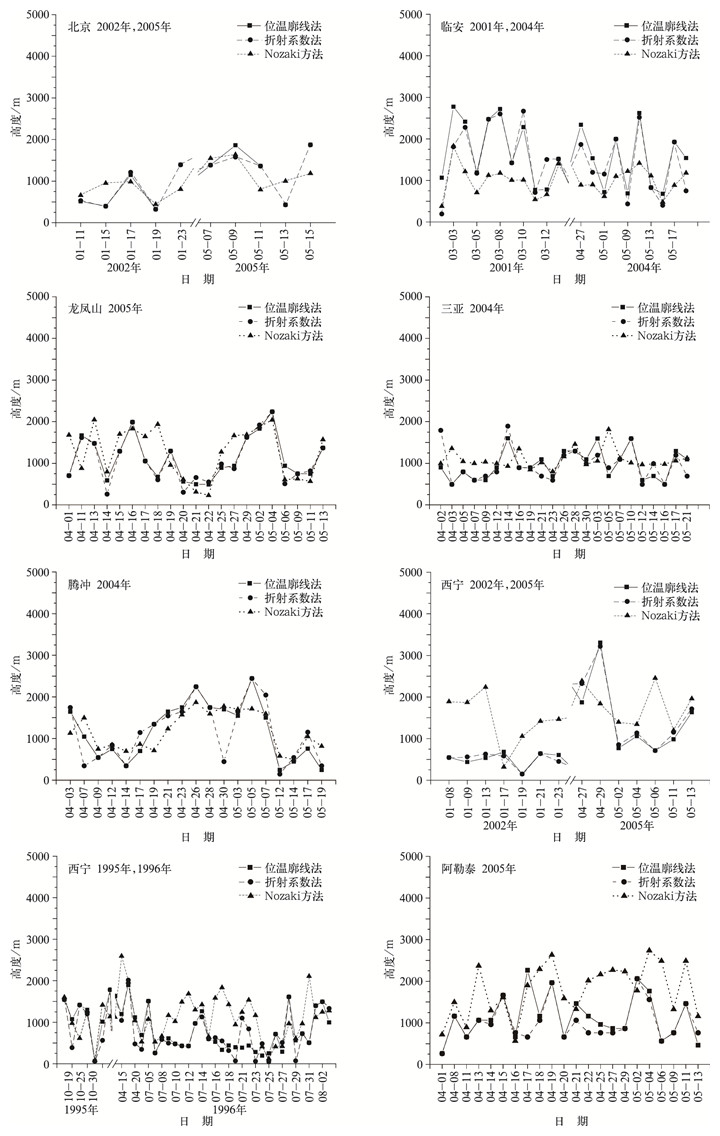
考虑各地气候特点的差异，在这里对表 1给出的7个站点的观测数据以及根据经验公式所确定的混合层厚度分别进行分析 (图 4)。

图 4

图 4. 龙凤山等7个站点由位温廓线法、折射系数法和Nozaki方法得到的混合层厚度对比 Fig 4. Mixing layer depths determined by potential temperature, refractivity profiles and Nozaki method at 7 sites

北京2002年和2005年计算的混合层厚度与位温廓线法或折射系数法所确定的混合层厚度的值相差不是很大，但个别点计算值明显地低于观测数据所确定的混合层厚度。

临安2001年和2004年计算值总体偏低，2001年3月尤其突出。从连续变化来看，计算的混合层厚度与折射系数和位温廓线法所确定的混合层厚度趋势总体上比较一致。

龙凤山除个别样本外，2005年计算值与位温廓线法或折射系数法所确定的混合层厚度相差不大，能反映混合层厚度逐日变化趋势。2005年4月18—27日放探空气球时云量都是10成，但与临安不同，计算混合层厚度与折射系数法和位温廓线法所确定的值相差不大。

三亚2004年计算值与位温廓线法或折射系数法所确定的值相差不大，同时折射系数法和位温廓线法所得混合层厚度基本在1000 m左右，而且计算值与气象探空观测所确定的值的逐日变化均比较小，混合层发展不强烈。计算值虽然与折射系数法或位温廓线法所确定的值相差不大，但是没有体现混合层逐日变化特征。考虑三亚临海，其边界层既类似陆地边界层，又受到海面边界层的影响，所以用Nozaki方法^[17]计算海陆结合地面的混合层可能不合适。

腾冲2004年计算值与位温廓线法和折射系数法所确定的混合层厚度值相差不是很大，而且能反映混合层厚度逐日变化。但2004年4月30日出现异常，折射系数法确定的混合层厚度低于经验计算值和位温廓线法确定值约1000 m。

西宁2002年1月和2005年气球放飞时间大约是14:00，与计算时间一致。2005年观测对比结果相一致，计算值与位温廓线法和折射系数法所确定的值偏离不大，能体现混合层逐日变化趋势。但是，2002年1月计算值明显高于位温廓线法和折射系数法所确定的值。造成这种原因可能还与春季和冬季温度较低、混合层的日增长不强烈有关。由于地形影响 (西宁的探空气球释放点在一山谷中)，西宁逆温层低、厚, 且污染比较严重，日照较弱，混合层发展较慢，不利于冬季混合层的增长。Nozaki方法^[17]并没有考虑地形因素，所以该方法在西宁冬季的使用可能高估混合层厚度。不同的是，北京2002年1月混合层计算值与位温廓线法、折射系数法确定值却比较接近，对比西宁2002年1月的情况，表明地形对Nozaki方法有一定影响。此外，北京作为超大城市，其热岛效应也可能促进了晴天混合层的发展。

西宁1996年7—8月的混合层厚度计算值明显高于位温廓线法所确定厚度，可能的原因是这段时间臭氧探空气球放飞的时间大约在11:00，早于计算时间14:00。由混合层增长理论，混合层在清晨开始增长，到午后达到最大值。放气球时间早于计算时间，在其间时间内，混合层很有可能增长所以导致计算值明显偏大。

阿勒泰2005年计算值偏高，但计算值与位温廓线法、折射系数法所确定的混合层发展变化趋势基本相同。由于阿勒泰地处我国西部地区，日出时间较东部地区晚，所以实际混合层发展过程稍晚于其他地区。14：00东部地区混合层可能已经达到日最高值，但是阿勒泰地区此时混合层厚度仍在发展增长中，这有可能是阿勒泰计算混合层厚度总体上大于气球探空曲线确定的混合层厚度的原因。

总体来看，龙凤山、腾冲、北京、西宁 (2005年) 这4了站点Nozaki方法计算的混合层厚度与气象探空观测所确定的厚度值相差不大，而临安、阿勒泰则较大，三亚的混合层计算值趋势也与观测数据所确定的值趋势相差较大，较难反映混合层发展的趋势。在所计算的7个站点中，Nozaki方法在其中4个站点有较好表现，与位温廓线法和折射系数法所确定的值偏离不大，并且能够反应混合层逐日变化趋势，这表明Nozaki方法具有一定实用性和可靠性。但是Nozaki方法没有考虑具体地形因素，如在西宁2002年1月和三亚的应用与气象探空曲线所得混合层差别较大。

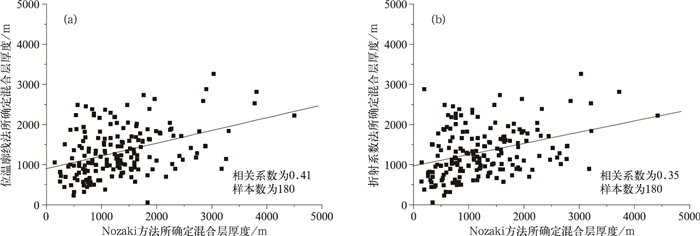
西宁1995—1996年释放气球的时间大约为10：00，比本文计算混合层厚度所选定的14：00早，考虑到此时混合层正处于增长阶段，所以应该剔除这段时间数据。图 5是剔除西宁1995—1996年数据后Nozaki方法与位温廓线法 (图 5a) 和折射系数法 (图 5b) 的比较。Nozaki方法与位温廓线法值计算结果的相关性稍好于其与折射系数法的相关性，这与折射系数法判别混合层厚度的准确程度以及大气稳定度有关 (见第3章)。为了找出Nozaki方法在不同混合层厚度时的误差大小，对混合层厚度每1 km进行分类计算了Nozaki方法分别相对于位温廓线法与折射系数法的误差平均值，从表 2可以看出，Nozaki方法计算所得混合层厚度相对于利用折射系数法和位温廓线法得出的混合层厚度在2 km以上偏低，在1 km以下偏高，且3 km以上偏差增大，1~2 km范围偏差较小。Nozaki方法与位温廓线法的混合层厚度之差稍小于其与折射系数法得到的混合层厚度之差。

图 5

图 5. Nozaki方法与探空曲线确定混合层厚度的比较 (a) 位温廓线法与Nozaki方法对比，(b) 折射系数法与Nozaki方法对比 Fig 5. Comparison of mixing layer depths determined by Nozaki method and radiosonde profiles (a) Nozaki method vs potential temperature profiles, (b) Nozaki method vs refractivity profiles

表 2

表 2 Nozaki方法计算值随不同混合层厚度与位温廓线法和折射系数法所确定值的差别 Table 2 Variations of mixing layer depths between Nozaki method and measurements of radiosonde profiles 混合层厚 度范围/m Nozaki方法与位温 廓线法差值/m Nozaki方法与折射 系数法差值/m 0~1000 443 553 1000~2000 -65 -108 2000~3000 -886 -931 3000以上* -1449 -1201 注：*由于3000 m以上厚度的混合层样本数比较少，所以3000 m以上混合层厚度归为一类。

表 2 Nozaki方法计算值随不同混合层厚度与位温廓线法和折射系数法所确定值的差别 Table 2 Variations of mixing layer depths between Nozaki method and measurements of radiosonde profiles

表 3列出7个站点3种方法确定混合层厚度的平均值及Nozaki方法计算值的相对误差。除了临安地区计算值偏小以外，其他地区均偏大。阿勒泰和西宁2002年1月计算值偏离程度较大，龙凤山、北京、三亚、西宁 (2005年)、腾冲偏离程度较小，偏离位温廓线值约11%~37%，与文献中所得结果比较接近^[14]，相对误差约为31%, 偏离折射系数值较大。

驱动混合层发展的动力主要来自太阳辐射，而云是影响太阳辐射的重要因素。因此，在这里以探空观测确定的值为参考，观察云对计算混合层厚度的误差影响。

表 3

表 3 不同方法所确定的龙凤山等7个站点混合层厚度平均值及相对误差 Table 3 Mean and relative error of mixing layer depths determined by 3 methods at 7 sites 地点 位温廓线法/m 折射系数法/m Nozaki方法/m Nozaki方法与位温 廓线法相对误差 Nozaki方法与折射 系数法相对误差 龙凤山 1125 1091 1266 0.13±0.53 0.33±0.78 北京 1536 1450 1403 0.11±0.56 0.23±0.74 临安 1597 1489 963 -0.26±0.51 -0.17±0.57 阿勒泰 1136 1013 1790 0.82±0.86 0.99±0.89 三亚 968 967 1091 0.29±0.57 0.30±0.54 西宁① 586 593 1422 2.27±2.07 2.19±1.98 西宁② 1798 1660 1927 0.31±0.74 1.02±3.11 腾冲 1130 1172 1184 0.37±0.81 0.52±1.24 注：① 为2002年1月的数据，② 为2005年4—5月的数据。

表 3 不同方法所确定的龙凤山等7个站点混合层厚度平均值及相对误差 Table 3 Mean and relative error of mixing layer depths determined by 3 methods at 7 sites

常规气象观测的总云量为0~10成，考虑样本数不多，本文将云对计算混合层厚度的误差的影响仅分成3组：Ⅰ表示总云量为0~2成，即无云；Ⅱ表示总云量为3~7成，即中量云；Ⅲ表示总云量为8~10成，即多云。

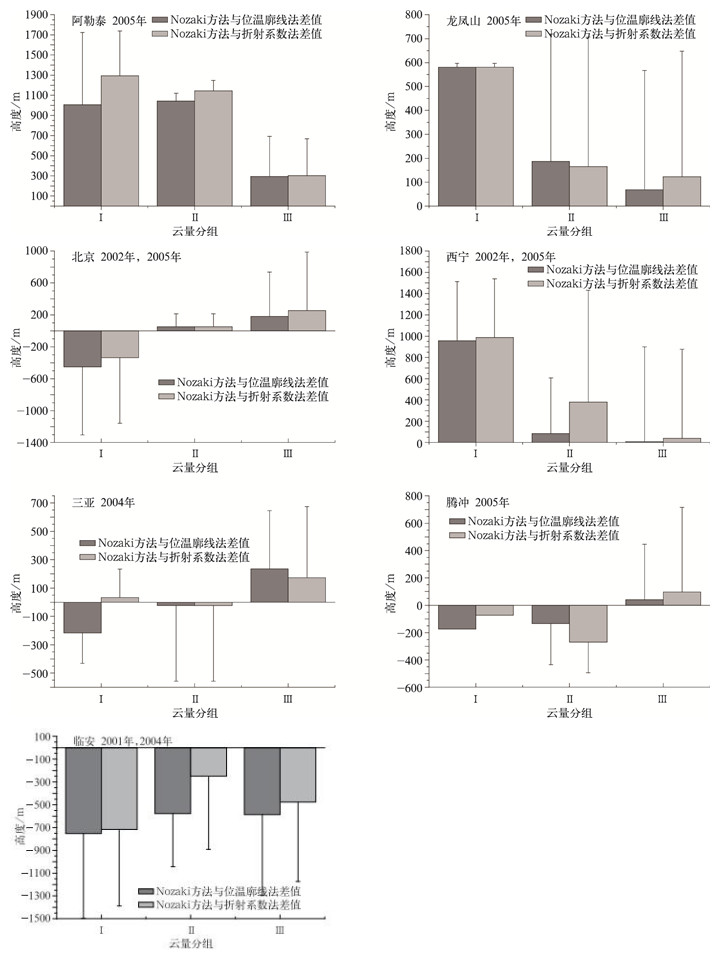
图 6给出了7个站点计算混合层厚度分别与位温廓线法和折射系数法所确定混合层厚度之间的差异，其中横坐标为云量分组, 直方图表示混合层之差的平均值与标准偏差，为了简洁，标准偏差仅给出正向值。差值的平均值在多云时较小，而在少云或者无云时较大，可见Nozaki方法受到不同云量的影响程度不同。多云天气下，一般大气层结较为稳定，稳定度P是影响混合层厚度发展的最重要因子，从混合层实际发展的程度来说，大气较为稳定时，混合层发展一般不强烈，其厚度小于1.5 km；从Nozaki方法的式 (1) 来说，多云天气下P值较大，其对公式的约束较大，式 (1) 中，较不稳定状况时偏小，所以Nozaki方法估计混合层厚度误差较小；但是少云无云天气下，混合层厚度发展的程度还依赖于风速、温度、日照辐射等多种因素，混合层厚度可能较高也可能较低，变化范围大，利用Nozaki方法来反映复杂的混合层发展，其计算结果的误差也增大。

图 6

图 6. 7个站点云量分组与不同方法确定的混合层厚度差值的关系 Fig 6. Differences of mixing layer depths categorized by cloud cover of 7 sites

此外，需要注意差值的标准偏差变化较大，因为也受到样本数和云量分组的影响，样本数较小也影响到数据的统计不稳定和代表性不足。但是图 6可以表明一个基本的特点：Nozaki方法计算结果在本文北方站点偏高 (阿勒泰，龙凤山，北京，西宁), 在南方站点偏低 (三亚，腾冲，临安)。

虽然位温廓线法与折射系数法所确定的混合层厚度的对应关系比较一致，但仍有个别样本差别很大 (如图 3箭头所示)，该样本为西宁2005年4月19日气球探空曲线所得结果。位温廓线法与计算值所得混合层厚度分别为2900 m和2883 m，但是折射系数法确定的厚度只有194 m，折射系数法确定混合层厚度失效。同样，腾冲2004年4月30日由折射系数法所确定混合层厚度为445 m，但是位温廓线法所确定厚度为1700 m，与计算值 (1777 m) 符合较好，该日天气为多云 (云量为8成)，大气层结较为稳定。由式 (2) 可知，折射系数法同时由水汽、气压和温度决定，当大气层结较稳定时，折射系数法随高度变化较剧烈，所以确定折射系数梯度极小值较难，折射系数法有可能失效，从而找不到真正的混合层厚度。对以上个例的分析反映了混合层厚度的确定影响因素很多，虽然同时使用位温廓线和折射系数法寻找混合层厚度，但是在大气层结较为稳定的条件下，仍有可能失败。同时这也是Nozaki方法计算混合层厚度与位温廓线法所确定厚度相关性较好于其与折射系数法所确定厚度的原因之一。

Nozaki方法计算混合层厚度具有明显的纬度依赖性。这种依赖性在2.2节中简单分析云与计算混合层厚度之间关系的结果中也可以看出，在北方站点偏高 (阿勒泰、龙凤山、北京、西宁), 在南方站点偏低 (三亚、腾冲、临安)。尽管在式 (1) 中考虑了纬度效应而引入的地转参数，但还不足以充分地表征纬度差异导致计算结果偏离实际观测结果的纬度特征。

此外，Nozaki方法并没有考虑地形的因素 (如山地、海滨、高原等地形特点)，仅引入了地表粗糙度Z₀来代表下垫面或者地表状况对混合层计算的影响，而敏感性试验也表明，Z₀的变化对Nozaki方法最后确定混合层厚度的影响不大 (图略)，而从物理过程来看，混合层的发展受下垫面影响显著，这也可能是该经验公式的一个不足之处。

1) 由位温廓线法和折射系数法所确定的混合层厚度一致性很好，同时用这两种方法来确定混合层厚度，可以使所得的混合层厚度更可靠。但是折射系数法偶尔出现寻找不到实际混合层厚度的情况，尤其在大气层结较为稳定时。

2) Nozaki方法可以较好地揭示混合层厚度的逐日变化特征，但具有明显的纬度效应。当实际混合层厚度大于2000 m时，计算结果偏低，主要出现在南方站点 (三亚、腾冲和临安)；而当混合层厚度小于1000 m时，计算结果偏高，出现在北方站点 (龙凤山、西宁、北京和阿勒泰)。

3) Nozaki方法计算结果较为明显地受到云量影响，多云时计算结果误差稍小，无云或少云时，计算结果误差增大。