2. 中国气象局成都高原气象研究所, 成都 610071;
3. 云南省气象台, 昆明 650034
2. Chendu Institute of Plateau Meteorology, China Meteorological Administration, Chendu 610071;
3. Meteorological Observatory of Yunnan Province, Kunming 650034
为了使更多的常规和非常规资料进入数值模式,得到更完美的初始场, 通常有三维和四维变分同化方法,但由于四维变分同化计算量较大,对计算环境要求较高,且需要模式的切线和伴随模式,比较复杂,因此在国内实际业务应用较少。而三维变分同化具有计算要求不高,能直接同化非常规观测资料的优点,是目前在研究和业务中普遍应用的同化方法。三维变分同化中代价函数用误差协方差来衡量背景场和各观测场中各因子的影响。根据最新资料统计,欧洲中期数值天气预报中心的同化系统生成的分析场只有15%的信息来自观测资料,其余85%的信息来自于背景场[1]。这说明决定背景场影响的背景误差协方差 (B) 在变分同化系统中是一个重要部分,极大影响分析场的质量。因此,在三维变分同化系统引进和应用中,对B的确定十分重要。国内外对B的分析和调整已有大量研究。如Ajjaji等[2]在同化试验中探讨了背景场误差和观测误差的作用,指出背景场误差和观测误差的调整工作应该对每个模式区域进行,以得到适合模式区域地理特征和分辨率的背景场误差和观测误差。龚建东等[3]通过NMC (National Meteorological Center) 方法[4]统计了T213L31模式的B,并利用观测余差方法对B中误差均方差和特征长度进行优化调整,结果表明:优化后的B,改善了全球模式预报效果。朱立娟[5]同样利用观测余差方法对用NMC方法统计出的B进行调整,应用于WRF (Weather Research and Forecast) 模式中,并进行个例试验,说明优化后的B更合理。范水勇等[6]利用NMC方法计算了MM5V3模式在北京地区冷暖季背景场误差,分析其特征,发现不同模式变量、水平分辨率、垂直层,不同季节背景误差特征不相同;并强调在资源充足情况下,应重新计算B[7]。刘磊等[8]研究了不同气候背景条件下B的性质,结果表明:B与天气背景、模式分辨率关系密切。曹小群等[9]讨论了区域模式中B在变分同化中的重要性,计算WRF模式1个月预报资料,利用NMC方法得到B,并讨论了B的结构特征。庄照荣等[10-11]利用观测余差方法对T213模式统计出B,并强调B的研究是一项基础性工作。我国格点模式GRAPES (Global and Regional Assimilation and Prediction System) 中的三维变分系统,对B进行了大量研究[12-16],结合我国实际,设计出适合格点模式的同化方案,通过变量变换对目标函数进行预调节,避免了直接计算B逆矩阵的困难。
以上研究讨论了B的特征及其合理性调整,而对应用不同B模式预报效果的试验较少,特别是在区域模式中利用不同B,模式预报效果如何?美国WRF中尺度模式及其同化系统在我国有广泛应用,也取得较好效果[17-22]。因此,选用WRF模式系统[23],积累模式预报场,利用其同化系统中的NMC方法进行B的统计,对B特征进行分析,通过单点理想试验验证其合理性,并利用模式自带的通用的B和重新统计的B进行数值试验,比较模式的预报效果。
1 背景误差协方差和NMC方法简介三维变分同化方法的思想是用变分方法解决求解最优分析值问题,即找到一个使得度量背景场和观测场之间的距离的目标函数极小的分析值,目标函数定义为
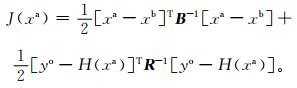
|
(1) |
式 (1) 中,J(xa),xa,xb,yo,H,B和R分别表示目标函数、分析变量场、背景场、观测场、观测算子、背景误差协方差和观测误差协方差。式 (1) 中,除了背景误差和观测误差协方差不确定,其他量为所求分析变量场、观测量和大尺度模式提供预报场。而观测误差协方差一般与观测仪器的观测误差有关,易确定,只有背景误差协方差较难确定。
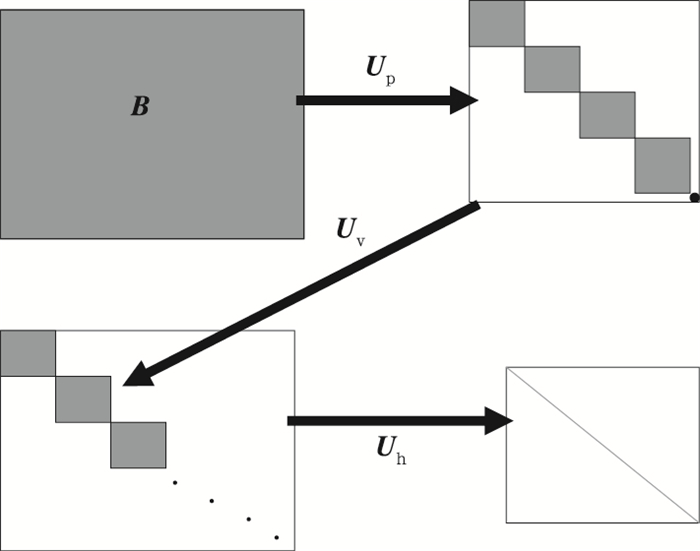
背景误差协方差在资料同化系统中的作用至关重要[8],它控制信息从观测位置向四周传播的方式,决定模式变量之间在动力上是否协调一致。在三维变分同化系统实现过程中, 由于B约为107×107的矩阵,超过了计算机存储能力,无法表示,B可以通过适当的控制变量转换来简化问题,控制变量变换U选择尽量满足关系式:
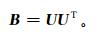
|
(2) |
它包括物理变换Up和空间变换,空间变换可分解为垂直变换Uv和水平变换Uh。从而控制变量转换和背景误差协方差分别表示为
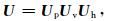
|
(3) |
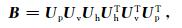
|
(4) |
简化过程如图 1所示。
|
|
| 图 1. 背景误差协方差与控制变量转换算子的关系 Fig 1. The relation between background error covariance and control variable transformation operator | |
在三维变分同化系统实现过程中, 首先进行物理变换,物理变量变换是为了消除模式变量之间的相关性而引入的,它利用平衡关系将模式变量分为平衡部分和非平衡部分,平衡部分描述变量之间的相关性,非平衡部分将作为分析变量。通过物理变换,将相关的模式变量转换为不相关的控制分析变量,从而B矩阵成为块对角矩阵 (图 1)。为了进一步简化,假定B值可以在水平和垂直方向上分离,接着进行垂直变换,垂直变换Uv的处理首先是通过估计背景误差协方差的垂直分量,然后通过经验正交函数EOF的特征模分解得到特征向量和特征值,再将控制变量空间的分析增量投影到模式层上。最后进行水平变换,水平变换是利用某种数学工具来近似描述背景误差水平相关模型,如递归滤波是处理水平相关的有效方法,其思想是利用变分同化需要得到Uh与1个向量的乘积,而并不是Uh本身;矩阵与向量相乘可以看成是一种滤波,这样就能利用信号处理领域已被广泛研究的滤波器来处理Uh。经过以上简化,B值统计量特征由3部分组成:① 物理变换中用于平衡变换的回归系数;② 垂直变换中垂直特征向量和特征值;③ 水平变换中用于递归滤波计算的特征长度。
NMC方法[4]假定预报误差的统计结构在一定预报时效内变化很小。这样,背景误差的空间相关近似于同一时刻、不同预报时效的预报之差的相关 (一般全球模式统计中为同一时刻的48 h预报减去24 h预报,区域模式中为24 h预报减去12 h预报)。NMC方法比较容易在业务上实施,能够得到模式变量在模式区域和所有模式层上与模式动力和物理上相协调的误差统计结构。NMC方法是目前数值天气预报业务中使用较为普遍的一种。
2 区域背景误差协方差统计量特征和单点试验 2.1 区域背景误差协方差统计量特征以同一时刻预报时效为12 h和24 h预报差的统计结构近似背景场误差结构。利用2008年5—10月逐日资料,运行WRF模式,每天分别从08:00和20:00(北京时,下同) 开始进行两次24 h积分。对于当天08:00而言,前1天的20:00 12 h预报减去前1天08:00 24 h预报作为预报误差;而当天20:00,则用当天的08:00 12 h预报减去前1天20:00 24 h预报作为预报误差。采用WRF3.0版本,区域为三重嵌套,第1重区域中心为26°N,99°E,分辨率分别为90 km×90 km,30 km×30 km,10 km×10 km;水平格点数分别为60×70,61×61,97×97。垂直方向分为35层;积云对流参数化方案三重区域分别采用Betts-Miller-Janjic, Kain-Fritsch, Grell-Devenyi ensemble;除积云对流参数化方案外,其他物理方案三重区域均一致:YSU边界层方案,Dudhia短波辐射方案和RRTM长波辐射方案。
在WRF模式中变分同化系统中的控制变量分别为流函数、非平衡速度势、非平衡温度、假相对湿度和非平衡地面气压。非平衡场被定义为完整场和平衡场之间的差。平衡场是通过指定的预测场 (这里是流函数φ) 进行回归分析得到,平衡速度势χb、平衡温度Tb、平衡地面气压psb和流函数之间的回归关系分别为χb(k)=c (k)φ(k), Tb(k)=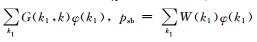
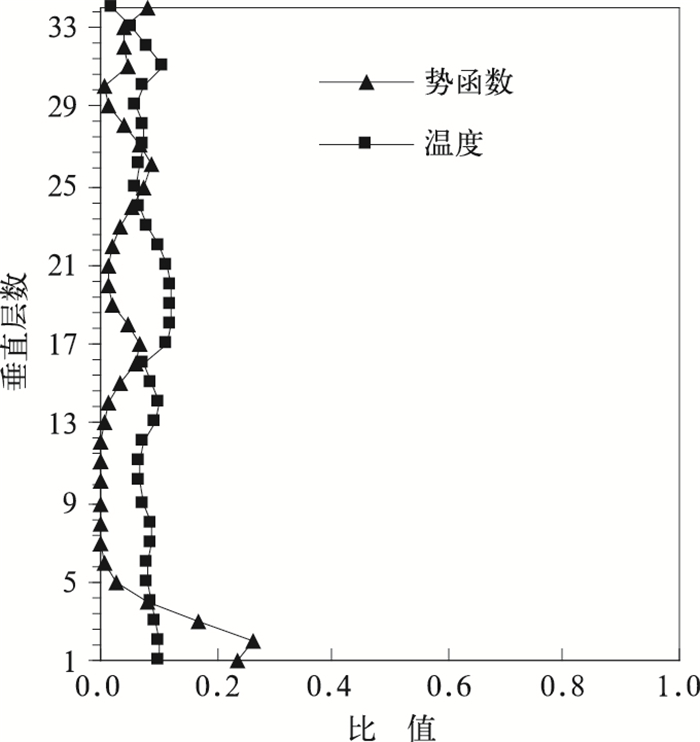
图 2表示平衡速度势、平衡温度与其完整场的比值系数随高度的分布。由于这里回归系数是选取整个水平点的平均,所以所有纬度上是相同的。速度势随高度分布反应了边界层的影响,在模式低层较大,高层较小。回归系数的大小与纬度关系较大,低纬度较小,随纬度增加而增大。统计区域为模式第1重网格,纬度约为2.44°S~53.51°N。由于所取区域为中低纬度,统计出的平衡部分势函数和温度与完整场的相关系数相对较小。地面气压的平衡部分与完整场的比值为0.16336,也比较小。
|
|
| 图 2. 平衡势函数、平衡温度与其完整场的比值 Fig 2. The ratio between balanced and full velocity potential, temperature | |
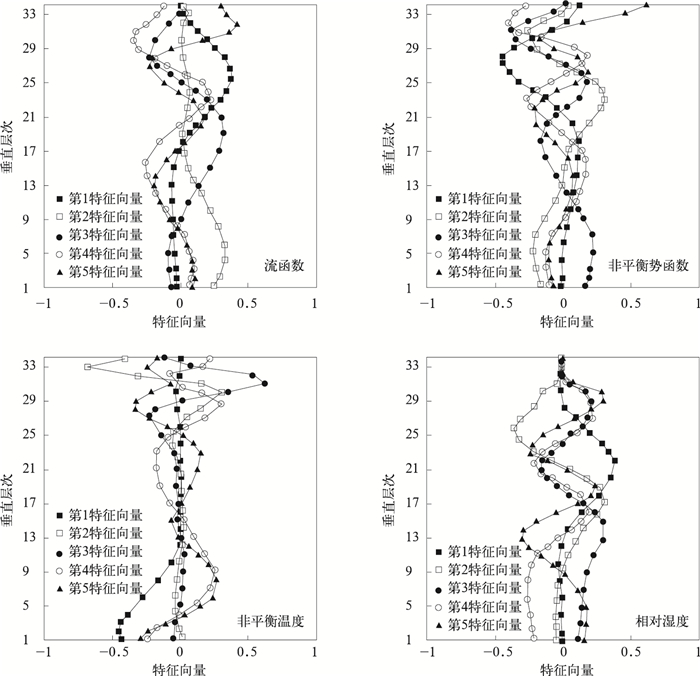
图 3和图 4分别为背景误差协方差垂直分量EOF分解后的前5个模态特征向量垂直分布和各模态的特征值。图 3中特征向量以特征值的大小为顺序。第1特征向量为主要特征模态 (特征值最大),它代表背景场误差分量的最主要结构,为大尺度模态。模数越高,垂直变化越多,基本上模数增加1个,垂直变化节点多1个。图 4为每个模态的特征值,即第1模态特征值最大,代表能量最多。模态数越大,特征值越小,能量越小。取99%能量进行截断,流函数、非平衡速度势、非平衡温度和相对湿度的截断模态数分别取15, 17, 24和22。
|
|
| 图 3. 控制变量的前5个特征向量 Fig 3. The five eigenvectors of control variables | |
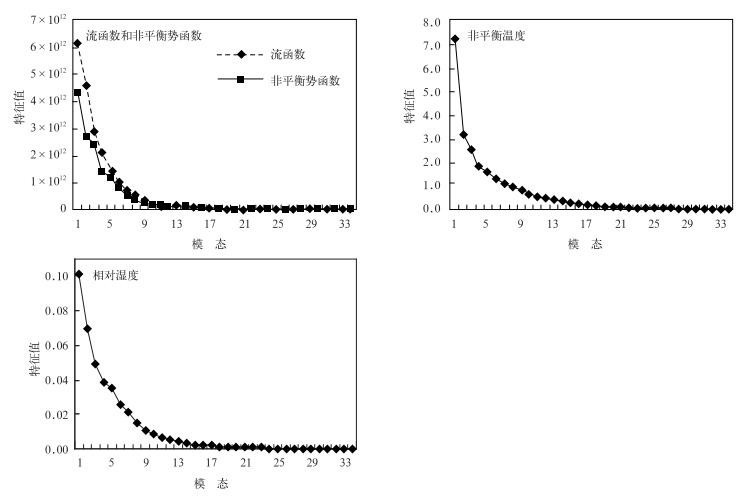
|
|
| 图 4. 控制变量各模态的特征值 Fig 4. The eigenvalues of control variables | |
特征长度尺度是递归滤波的一个重要参数,表征了背景误差影响的水平范围。图 5为控制变量特征长度尺度在各个垂直特征模态上的分布。第1模态影响尺度最大,模态越高影响尺度越小 (相对湿度最后3个模态除外)。流函数和非平衡速度势较非平衡温度和相对湿度特征尺度大,反映了温度和湿度是局地变量。即温度和湿度观测和背景场的偏差对分析场的影响主要集中在观测位置周围的模式格点上。
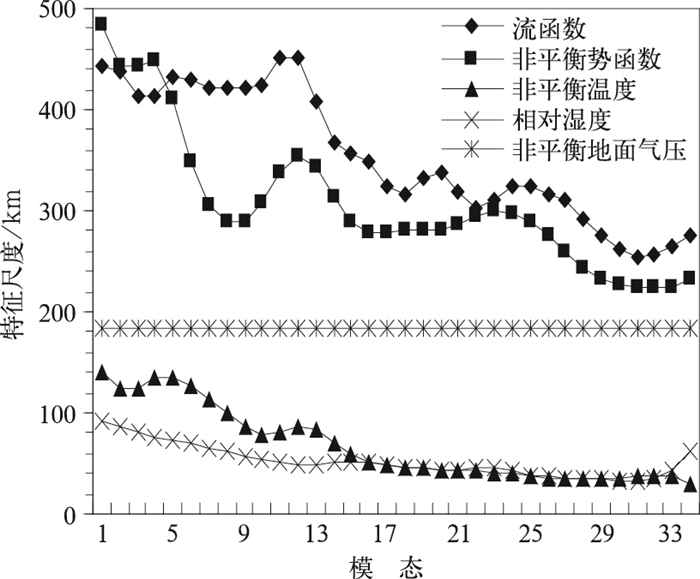
|
|
| 图 5. 分析变量特征长度尺度分布 Fig 5. Lengthscales of control variables | |
2.2 单点试验
为了验证统计的B的正确性和合理性,通常进行单点理想试验。试验取模式第1重嵌套范围 (水平分析区域取60×70个格点,格距90 km,垂直方向35层),背景场取2008年3月31日08:00的NCEP/GFS资料。观测值和观测误差由人为给定,在模式的第30(南北) 格点、第35(东西) 格点、垂直方向第24层,分别给定观测场与背景场的差 (新息向量) 为1 m·s-1的纬向风和1 K的温度,观测误差分别为1 m·s-1和1 K。单点理想试验的结果反映B的结构。
图 6给出了纬向风单点观测同化试验分析增量场 (第24层) 分布。同化后的纬向风分析增量场 (图 6a),形成了自内向外逐步减少的椭圆环分布,中心增量最大,向外逐步减小,且外围西南、东北方向产生小的东风增量。影响范围较大,与前面背景误差协方差中流函数特征长度较大的统计结果 (图 5) 相一致。经向风分析增量场 (图 6b),分析区域内垂直坐标轴向右旋转30°左右,第1、第3象限为南风,第2、第4象限为北风,同时该层气压和温度的增量 (图 6c,6d),都有向右旋转。与经典的风压场地转平衡有所差别。主要是由于B统计的范围是中低纬度地区,同化分析的量平衡部分占总量的部分比较小 (图 1),所以出现非平衡的旋转。经向风单点试验结果与纬向风单点试验结果类似,也有向右旋转的现象 (图略)。
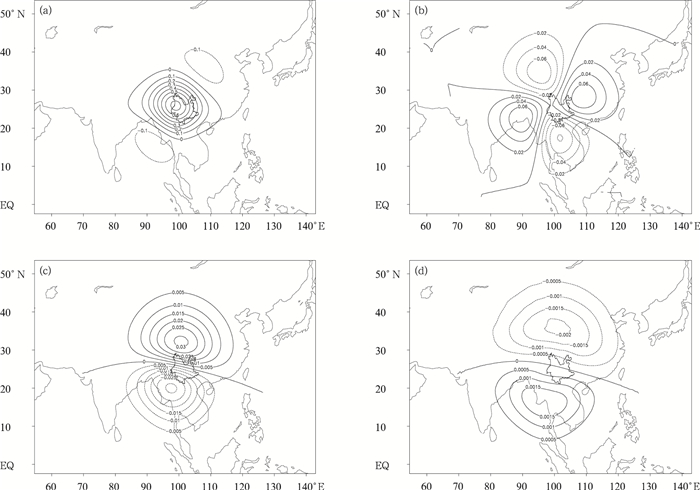
|
|
| 图 6. 纬向风单点观测同化试验 (a) 纬向风分析增量场 (单位:m·s-1),(b) 经向风分析增量场 (单位:m·s-1),(c) 气压分析增量场 (单位:Pa),(d) 温度分析增量场 (单位:K) Fig 6. The assimilation test of zonal wind speed single observation (a) zonal wind increment structure (unit:m·s-1), (b) meridional wind increment structure (unit:m·s-1), (c) pressure increment structure (unit:Pa), (d) temperature increment structure (unit:K) | |
图 7为温度单点观测同化试验分析增量场分布。温度场分析增量场 (图 7a),形成了自内向外逐步减少的圆环分布,其范围较小。与前面背景误差协方差特征长度统计结果 (图 5) 一致,即温度特征长度较表示风场的流函数和地面气压都小,为局地量。由于温度场平衡部分与流函数相关,从而分析风场也产生增量如图 7b,7c所示,为一反气旋。由于温度平衡部分占总的温度比例较小,所以从量值上看,风场增量较小。由于平衡和非平衡量的共同作用,风场有右旋。地面气压由于与流函数有相关性,气压产生相应的增量 (如图 7d所示)。
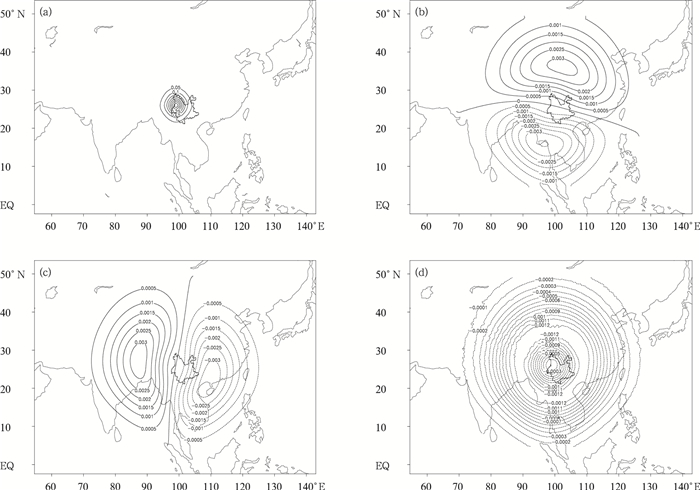
|
|
| 图 7. 温度单点观测同化试验 a) 温度分析增量场 (单位:K), (b) 纬向风分析增量场 (单位:m·s-1),(c) 经向风分析增量场 (单位:m·s-1),(d) 气压分析增量场 (单位:Pa) Fig 7. The assimilation test of temperature single observation a) temperature increment structure (unit:K), (b) zonal wind increment structure (unit:m·s-1), (c) meridional wind increment structure (unit:m·s-1), (d) pressure increment structure (unit:Pa) | |
单点理想试验结果表明,利用重新统计的背景误差协方差进行的三维变分分析结果与经典的位势高度场及风场的背景场误差水平相关模型[24](即地转平衡关系) 不完全一致,与B值统计特征一致,平衡部分占总量比例较小有关。增量影响范围与特征尺度大小一致,量值范围合理。因此,重新统计的B反映中低纬度地区非地转平衡关系,且反映多变量之间的相互作用关系,结构合理。
WRF模式系统中的同化模块自带了通用的B(CV3-B)[25],利用CV3-B也能实现同化。CV3-B是通过美国NCEP的GFS模式T170分辨率的24 h和48 h的预报,累加了357个时次,用NMC方法统计得到。CV3-B的统计与本地化B统计方法在垂直方向有所区别,CV3-B通过递归滤波进行分析而不是用EOF分析特征值和特征向量的方法。为了比较两种B的具体差别,这里用CV3-B做同样位置和层次的单点理想试验,图 8为纬向风和温度单点试验的部分增量分析结果,从纬向风增量看,与应用本地化B单点试验结果 (图 6a) 相比,影响范围稍大,且中心值为0.9 m·s-1,较本地化的0.7 m·s-1大,经向风增量也较大,说明CV3-B的水平风场的特征尺度和方差都较本地化B大。从图 8a,8b看,风场增量分布对称,说明满足地转平衡关系。从温度单点试验结果看 (图 8c,8d),温度增量中心量值为0.35 K,较应用本地化B(图 7a) 的0.4 K小,但增量影响范围明显扩大。纬向风增量基本南北对称,中心量值0.07 m·s-1较本地化B(图 7b)0.003 m·s-1大,说明CV3-B的温度方差较小,而特征尺度较大。从理想试验结果看,两种不同的B,在方差、特征尺度以及各种量之间相关关系都有所差别。特别是本地化B平衡关系较弱,而CV3-B基本满足地转平衡关系。
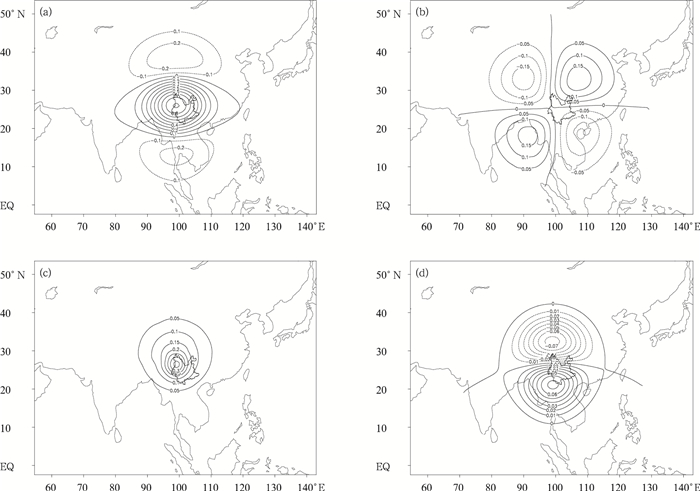
|
|
| 图 8. 纬向风 (a,b) 和温度 (c,d) 单点观测同化试验 (a) 纬向风分析增量场 (单位:m·s-1),(b) 经向风分析增量场 (单位:m·s-1),(c) 温度分析增量场 (单位:K), (d) 纬向风分析增量场 (单位:m·s-1), Fig 8. The assimilation test of zonal wind (a, b) and temperature (c, d) single observations (a) zonal wind increment structure (unit:m·s-1), (b) meridional wind increment structure (unit:m·s-1), (c) temperature increment structure (unit:K), (d) zonal wind increment structure (unit:m·s-1) | |
3 不同数值试验结果分析
利用WRF模式系统自带的CV3-B,以及根据自身模式区域2008年5—10月预报统计得到本地化B进行预报试验。预报试验中,模式背景场均为NCEP/GFS资料,同化常规地面高空资料,模式除同化系统中B不同外,模式其他参数均相同。试验时间为2009年6月1—30日,每天14:00起报的6 h预报,即到20:00,进行常规地面和高空资料的同化,同化后进行24 h预报,对同化过程和预报结果进行分析比较。
2009年6月,云南省出现4次大雨过程 (按照云南省气象台标准,全省大雨及以上量级降水站数达到22站及以上为1次大雨过程)。选取一次切变线为主要影响系统的降水过程 (6月30日20:00—7日1日08:00) 进行分析。为了更好地分析同化差别,只选取滇西的腾冲站 (25.02°N,98.5°E) 探空资料进行同化。图 9为700 hPa的风矢量场。2009年6月30日20:00,初始场的切变线位于石屏—景东—大理一线 (图 9a)。应用本地化B(图 9b) 和CV3-B(图 9c) 进行同化后的风矢量增量进行比较,发现CV3-B的整体风矢量增量较本地化B的大,并且增量范围较大,影响了整个模拟区域。切变线所在区域为一致的西风增量,使切变东推减弱,相对影响范围过大,不合理;而本地化B影响范围较小,且在切变线附近增量有风向的变化,相对合理,使切变线有所增强。风矢量的增量与前面分析的本地化B方差和特征尺度都较CV3-B偏小相一致。图 10为2009年6月30日20:00—7月1日08:00降水,从降水实况看 (图 10a),降水基本发生初始场切变线的南侧。应用CV3-B模拟的降雨带 (图 10b) 基本与实况一致,但强中心较实况偏北,滇西德宏地区有大暴雨的空报。应用本地化B(图 10c, 10d),在切变线南侧附近有5~10 mm降水加强,与前面风矢量增量使切变线增强相一致。强降水中心略南移,滇西的空报有5~10 mm的减弱,模拟降水较CV3-B接近实况。CV3-B一致的西风增量使切变线略东移,从而降水范围较本地化B略大,因而在切变线附近出现本地化B模拟的降水有所减弱。整体上看,应用本地化B的同化后的增量合理,降水模拟更接近实况。
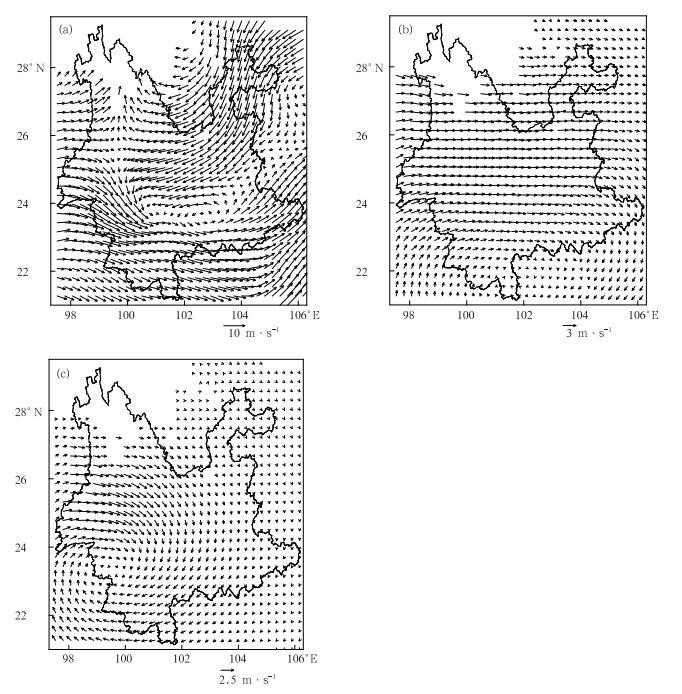
|
|
| 图 9. 2009年6月30日20:00 700 hPa风矢量 (a) 初始场, (b) 应用CV3-B的增量场, (c) 应用本地化B的增量场 Fig 9. The wind vector fields of 700 hPa at 20:00 30 June 2009 (a) initial guess field, (b) the increment field using CV3-B, (c) the increment field using the updated B | |
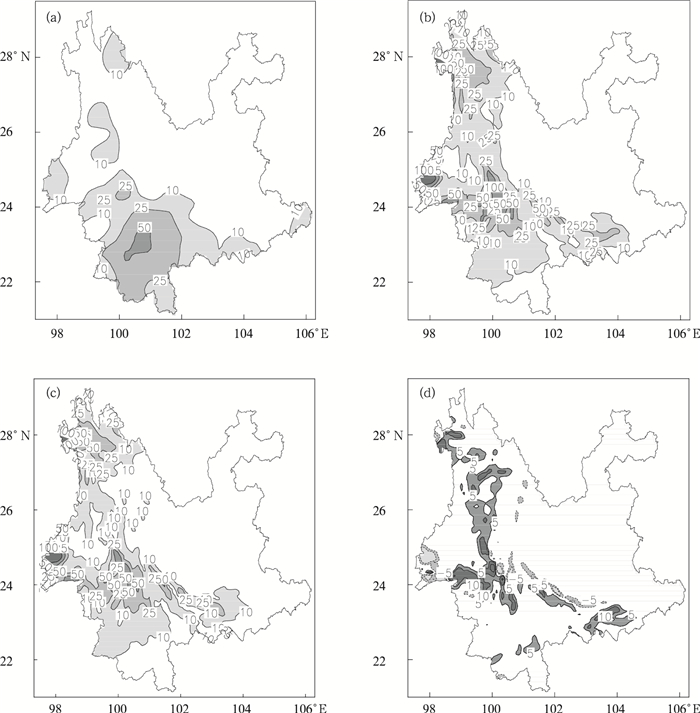
|
|
| 图 10. 2009年6月30日20:00—7月1日08:00降水量 (单位:mm) (a) 实况,(b) 应用本地化B模拟,(c) 应用CV3-B模拟,(d) 模拟差值 (本地化B-CV3-B) Fig 10. Accumulated precipitation from 20:00 30 June to 08:00 7 July in 2009(unit:mm) (a) observation, (b) simulated precipitation using updated B, (c) simulated precipitation using CV3-B, (d) the difference of simulated precipitation with different B(updated B minus CV3-B) | |
应用常规地面和高空资料对2009年6月进行不同B模拟试验。对同化过程中目标函数和梯度进行比较发现。从迭代的过程看,最小化收敛标准均为0.01,应用本地化B同化迭代20步左右,而利用CV3-B迭代步数为40步左右。并且应用本地化B,除了少数步数有波动,其他迭代步均为单调下降,而且下降速度较快,而CV3-B则在下降过程中波动较多,下降速度较慢。从同化过程看,利用本地化B效率更高、收敛更稳定。
对2009年6月逐日模拟结果进行24 h降水检验,检验区域为模式的第3重区域,即云南省范围,降水检验结果如表 1所示。综合TS评分、公平TS评分 (ETS) 和预报偏差,小雨量级,CV3-B的预报效果略好;中雨及以上量级降水,应用本地化B进行常规地面高空资料同化后模式模拟的效果优于CV3-B的。从降水分布上看,中雨预报偏差略大于CV3-B的,大雨和暴雨量级的偏差都较CV3-B接近1,特别在大雨量级上的差别较明显。
|
|
表 1 CV3-B和本地化B作为背景误差协方差WRF模式降水预报检验 Table 1 The precipitation forecast test with CV3-B and updated B in WRF |
4 小结
利用WRF模式三维变分同化系统,用NMC方法重新统计了背景误差协方差,对背景误差协方差结构特征进行分析,并通过单点理想试验进行验证,发现通过WRF模式同化系统NMC方法统计B的结构合理。并通过模式自带的通用B与重新统计的B进行模拟试验,试验结果表明,不同的B,同化过程差别较大,应用本地化B同化后,初始场变化的尺度和大小较合理。同化效率更高,目标函数收敛更稳定。降水模拟的分布差别较大。通过降水检验评分发现,应用本地化B同化后模拟的降水在中雨及以上量级预报效果有所改进。小雨量级预报效果略差。说明背景误差协方差的重新统计对模式预报效果改进有一定作用,在应用三维变分同化系统时,重新统计B十分必要。
但这里试验过程中模式同化的资料相对较少,仅用了常规地面和高空资料,对资料同化后模式降水预报效果影响相对小。同化更多资料,如GPS/PWV、自动站资料和卫星、雷达等资料的试验,以及更长时间的预报检验,有待下一步研究。
致谢 本文得到美国国家大气研究中心 (NCAR) 的黄向宇老师、刘志权老师和张昕老师的耐心指导,在此一并表示感谢。| [1] | Cardinali C, Pezzulli S, Anderson E. Influence-matrix diagnostic of a data aysimilation system. Quart J Roy Meteor Soc, 2004, 130: 2767–2786. DOI:10.1256/qj.03.205 |
| [2] | Ajjaji Radi, Al-Katheri A A, Dhanhani A.Tuning of WRF 3D-Var Data Assimilation System over Middle-East and Arabian Peninsula.The 8th WRF User Workshop, 2007. |
| [3] | 龚建东, 赵刚. 全球资料同化中误差协方差三维结构的准确估计与应用:背景误差协方差调整与数值试验分析. 气象学报, 2006, 64, (6): 669–682. DOI:10.11676/qxxb2006.065 |
| [4] | Parrish D F, Derber J C. The National Meteorological Center's spectral statistical interpolation analysis system.Mon Wea Rev, 1992, 120: 1747-1763. Mon Wea Rev, 1992, 120: 1747–1763. DOI:10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2 |
| [5] | 朱立娟. 背景场误差协方差估计技术的应用研究. 南京: 南京信息工程大学, 2005: 1-60. |
| [6] | 范水勇, 张朝林, 仲跻芹. MM5三维变分系统在北京地区冷暖季背景场误差的对比分析. 高原气象, 2006, 25, (5): 855–861. |
| [7] | 范水勇, 郭永润, 陈敏, 等. 高分辨率WRF三维变分同化在北京地区降水预报中的应用. 高原气象, 2008, 27, (6): 1181–1188. |
| [8] | 刘磊, 费建芳, 程小平, 等. 我国东部海区不同气候背景条件下背景误差协方差的性质对比分析. 海洋预报, 2009, 26, (4): 25–35. DOI:10.11737/j.issn.1003-0239.2009.04.004 |
| [9] | 曹小群, 黄思训, 张卫民, 等. 区域三维变化同化中背景误差协方差的模拟. 气象科学, 2008, 28, (1): 8–14. |
| [10] | 庄照荣. 背景场误差的结构特征及其对三维变分同化影响的研究. 北京: 中国气象科学研究院, 2004: 1-87. |
| [11] | 庄照荣, 薛纪善, 庄世宇, 等. 资料同化中背景场位势高度误差统计分析的研究. 大气科学, 2006, 30, (3): 533–544. |
| [12] | 张华, 薛纪善, 庄世宇, 等. GRAPES三维变分同化系统的理想试验. 气象学报, 2004, 62, (1): 31–41. DOI:10.11676/qxxb2004.004 |
| [13] | 黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现. 应用气象学报, 2005, 16, (3): 374–384. |
| [14] | 庄世宇, 薛纪善, 朱国富, 等. GRAPES全球三维变分同化系统——基本设计方案与理想试验. 大气科学, 2005, 29, (6): 872–884. |
| [15] | 马旭林, 庄照荣, 薛纪善, 等. GRAPES非静力数值预报模式的三维变分资料同化系统的发展. 气象学报, 2009, 67, (1): 50–60. DOI:10.11676/qxxb2009.006 |
| [16] | 薛纪善, 陈德辉. 数值预报系统GRAPES的科学设计与应用. 北京: 科技出版社, 2008: 1–61. |
| [17] | 刘红亚, 薛纪善, 沈桐立, 等. 探空气球漂移及其对数值预报影响的研究. 应用气象学报, 2005, 16, (4): 518–526. |
| [18] | 陈炯, 王建捷. 北京地区夏季边界层结构日变化的高分辨模拟对比. 应用气象学报, 2006, 17, (4): 403–411. |
| [19] | 徐广阔, 孙建华, 雷霆, 等. 多普勒天气雷达资料同化对暴雨模拟的影响. 应用气象学报, 2009, 20, (1): 36–46. |
| [20] | 苗世光, 孙桂平, 马艳, 等. 青岛奥帆赛高分辨率数值模式系统研制与应用. 应用气象学报, 2009, 20, (3): 370–379. |
| [21] | 董佩明, 王海军, 韩威, 等. 水物质对云雨区卫星微波观测模拟影响. 应用气象学报, 2009, 20, (6): 682–691. |
| [22] | 仲跻芹, 陈敏, 范水勇, 等. AMDAR资料在北京数值预报系统中的同化应用. 应用气象学报, 2010, 21, (1): 19–28. |
| [23] | Skamarock W C, Klemp J B, Dudhia J, et a1.A Description of the Advanced Research WRF Vesion 3.NCAR Tech Note, NCAR/TN-475+STR, 2008:125. |
| [24] | Wu W S, Purser R J, Parrish D F. Three dimensional variational analysis with spatially inhomogeneous covariance. Mon Wea Rev, 2002, 130: 2905–2916. DOI:10.1175/1520-0493(2002)130<2905:TDVAWS>2.0.CO;2 |
| [25] | Derber J, Bouttier F. A reformulation of the background error covariance in the ECMWF global data assimilation system. Tellus, 1999, 51: 195–221. DOI:10.3402/tellusa.v51i2.12316 |
 2011, 22 (4): 482-492
2011, 22 (4): 482-492



