2. 国家气象中心,北京 100081
2. National Weather Center, Beijing 100081
随着社会的发展和人民生活水平提高,人们对气象服务提出了更多、更高的要求。温度是与人们日常生活息息相关的气象要素。数值预报产品释用技术被认为是提高温度预报水平最直接、最有效的途径,近些年也取得了一系列成果[1-6]。很多气象部门都开始利用模式输出统计方法 (Model Output Statistics,简称MOS) 来制作精细化温度预报[7-9]。
基于MOS假设建立温度预报方程通常需要一定长度的历史资料样本,在建模历史样本足够多的情况下,采取分月建立预报方程的方案更为合理。在实际情况中,由于模式历史样本数的限制,通常是假设同一季节具有相似的气候变化规律,同时具有相同的预报因子与预报要素的关系,在建立温度预报方程时,按季节来考虑,预报时按季节选取相应的方程来做预报。因此,季节划分方式是否合理,对预报效果有直接影响。现在国内基于MOS思想的温度预报中,季节通常是按照春、夏、秋、冬4个季节来划分。陈豫英等[9]对宁夏25个测站48 h逐时温度预报时,在考虑宁夏气温季节性变化的基础上, 将资料按自然季节划分为春 (3—5月)、夏 (6—8月)、秋 (9—11月)、冬 (12月—次年2月)4个季节。刘还珠等[10]利用全国两千多个台站资料, 采用MOS方法制作温度预报。将资料按自然季节, 以12月—次年2月、3—5月、6—8月、9—11月划分为冬、春、夏、秋4个季节,为克服样本量偏少, 也考虑季节偏早或偏晚问题, 将每季分别向前后跨半个月, 如春季为2月16日—6月15日、夏季为5月16日—9月15日等。但是,关于这种季节划分方式是否合理、不同区域是否应该采取不同的季节划分方式等方面的研究还比较少。
本文通过采用K-means聚类方法,对华北地区进行了季节划分试验。提出了一种新的季节划分方式,更有利于将具有相似气候特征的日期划分为一类,与传统季节划分方式相比,具有明显优势,预报效果有一定改进。
1 资料与方法 1.1 资料本文所用资料包括2003—2009年T213模式的基本量和诊断量预报场资料;华北地区154个测站2003—2009年1日8次的温度观测资料以及日最高、最低温度资料。需要说明的是这个时间段,具有清晰的年代际背景特征 (全球变暖),如果气候特征有较大变化时,本文得到的结果可能不再适用,需要重新进行分析。
1.2 方法 1.2.1 MOS方法简介Glahn等[11]1972年首先提出了模式输出统计法, 在美国的气象业务预报中替代Klein等[12]1959年提出的完全预报法 (Perfect Prognostic Method,简称PP)。MOS预报方法的基本思想是当时天气情况取决于当时环流背景, 因而在建模过程中预报量与预报因子的统计关系具有一致性。具体做法是先从数值模式的回算资料中选取合适的预报因子,然后与预报量的历史实况资料一起建立预报方程,预报时代入所用模式的预报因子,就可以得到所要预报的要素值。MOS方法对模式的系统性误差有明显的订正能力,不要求模式有很高的精度,只要模式预报误差特征稳定,就可以得到比较好的MOS预报结果,从而提高预报准确率。本文利用MOS方法对两种不同的季节划分方式进行温度预报效果的对比分析。
1.2.2 K-means算法简介K-means算法[13-14]属于数据挖掘聚类分析方法中一种最基本的、应用最广泛的划分算法。它是一种已知聚类类别数的聚类算法,可以将N个样本划分为K类 (N>K),聚类数目K为输入的参数。选取K个观测量即K个聚类中心点,也称为初始类中心。按照距这几个类中心的距离最小原则将观测量分派到各类中心所在类, 形成第1次迭代后的结果K类。根据组成每一类的观测量计算各变量均值,每一类的N个均值又形成了K个点,这就是第2次迭代的类中心。按照这种方法迭代下去,直到达到指定的迭代次数或中止迭代的判据要求时,迭代停止,聚类结束。本文采用K-means算法进行季节划分试验。
2 华北地区季节划分试验在华北地区选取154个测站进行季节划分试验,在考虑华北地区地形、气候特征的前提下,从要素场和环流形势场两个方面进行聚类分析[15]。经过多次试验,不同的收敛判据得到的分析结果较为一致,文中采取的收敛判据是0.01。
2.1 要素场聚类分析结果分别选取日最高温度、日最低温度和日平均温度等3个要素进行分析。对2003—2008年的实况温度资料做年平均处理,采用K-means算法进行聚类分析,对应传统的春、夏、秋、冬4季节的划分,将所有样本分为4类,结果如图 1所示。从图 1可以看到,最高温度、最低温度和日平均温度得到了相似的聚类结果,由于聚类结果是将具有相同变化趋势的天划为一类,反映季节变化的趋势,因此从不同侧面说明了聚类结果的合理性。同时,从图 1可以看到,季节划分与传统季节划分方式存在明显差异,原来的春秋两季被划分为不连续的两类,2月初到3月中旬与11月初到12月初有着相似的特征,被划分为一类,而3月下旬到4月底与10月初到11月初特征相似,被划分为另一类。原来的冬、夏两季划分变化不大,只是在时间长度上有些差异。
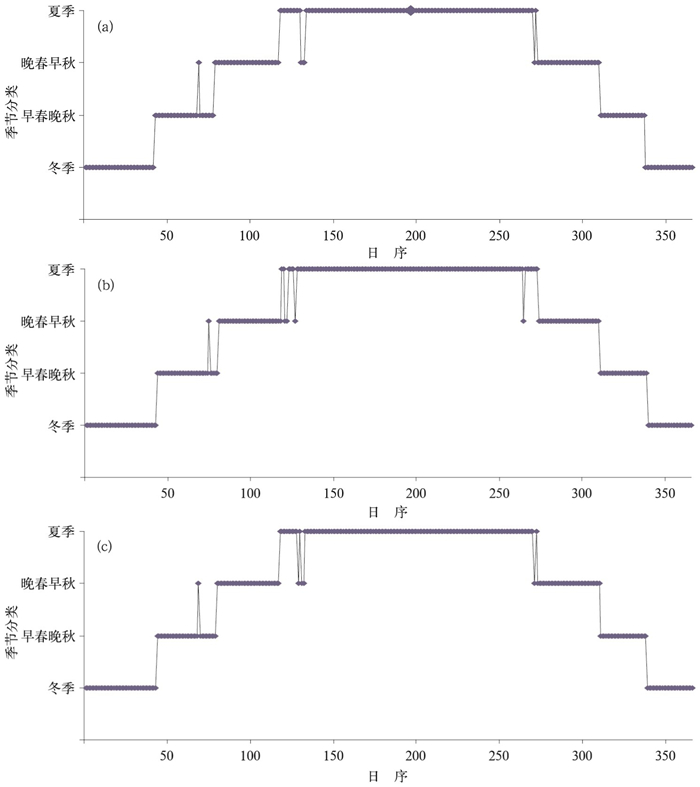
|
|
| 图 1. 华北地区要素场的聚类分析结果 (a) 最高温度, (b) 最低温度, (c) 平均温度 Fig 1. The cluster analysis result of element fields in North China (a) maximum temperature, (b) minimum temperature, (c) average temperature | |
2.2 环流形势场聚类分析结果
对要素场进行了季节划分试验结果表明:不同的要素得到了一致的季节划分结果。选取0 h和24 h时效500 hPa高度场、24 h时效700 hPa温度场、0 h和24 h时效700 hPa纬向风和经向风场,将这些物理量场综合在一起进行分析。首先进行标准化处理,然后通过聚类将具有相近变化趋势的天划为一类。从图 2可以看到,环流形势场的聚类结果与要素场的聚类结果显示出很好的一致性,与传统的季节划分方式相比, 主要差异是原来的春、秋两季被重新分类,其中靠近夏季的部分被分为了一类,靠近冬季的部分被分为了另一类。

|
|
| 图 2. 华北地区环流形势场的聚类分析结果 Fig 2. The cluster analysis result of circulation fields in North China | |
从要素、环流形势多方面进行季节划分试验,得到了比较一致的结果,说明这种季节划分方式是合理的。根据以上的分析,定义一种新的季节划分方式:2月11日—3月20日和11月5日—12月4日为早春晚秋类,5月1日—9月30日为夏季类,3月21日—4月30日和10月1日—11月4日为晚春早秋类,12月5日—2月10日为冬季类。
3 预报模型的建立 3.1 预报因子的选取选取合适的预报因子至关重要。本文所用到的预报因子涵盖了15个基本层次以及11个层间差,除了各层的高度、温度、相对湿度、纬向风、经向风和散度、涡度等基本预报场之外,还包括某些层次的温度露点差、位温、假相当位温、垂直速度、螺旋度、Q指数、湿位涡等。这样, 一方面扩大因子选取的范围, 另一方面也在一定程度上考虑了预报对象与预报因子之间的非线性关系。将格点的数值预报值插值到站点上作为预报因子,然后与站点上的预报对象建立预报方程[16]。
3.2 建立MOS预报方程在这里采用双重检验的逐步回归方法[17],它综合了逐步回归和逐步剔除两者优点。其基本思路是将一个个显著因子引入,在每引入一个因子的同时,对已引入的因子进行检验,剔除不显著因子,直到最后既不能引入因子也不能剔除因子为止。预报因子数量并不是越多越好,需选取与预报要素相关性大而且相互独立的因子,经过试验发现,取4~20个因子建方程预报效果最佳,在这里通过调整F值来控制因子数目,因子的选取随预报时效变化不大。对比方案如下:
方案一:选择传统的四季划分方式,分别为春季 (3月1日—5月31日)、夏季 (6月1日—8月31日)、秋季 (9月1日—11月30日)、冬季 (12月1日—次年2月28日)。
方案二:按照聚类分析的结果,划分新四季,分别为早春晚秋类 (2月11日—3月20日和11月5日—12月4日)、夏季类 (5月1日—9月30日)、晚春早秋类 (3月21日—4月30日和10月1日—11月4日)、冬季类 (12月5日—次年2月10日)。
利用2003—2008年的资料分别建立预报方程,2009年相应的时间段进行试报,以下是试报结果的检验分析。
4 预报结果检验因为新的季节划分与传统的季节划分方式的主要区别是春季和秋季的划分,夏季和冬季相比传统的季节划分变化不大,只是时间长度上存在差异,所以本文以2009年3—5月和9—11月这两段时间作为代表进行检验,分析两种不同季节划分方案对温度MOS预报效果的影响。
4.1 平均绝对误差对比温度预报的平均绝对误差是衡量预报效果的根本指标,因此先就两种季节划分方案最高温度和最低温度预报的平均绝对误差进行对比分析。
图 3给出的是两种季节划分方案最高温度和最低温度预报平均绝对误差。从图 3可以看到:除3—5月最高温度外,9—11月最高温度和3—5月以及9—11月最低温度预报结果都显示方案二的预报误差小于方案一,尤其是9—11月最高温度和最低温度预报误差相对于方案一都有明显的下降;3—5月最高温度预报,方案二误差等于或者略大于方案一,但是差异不大。因此从整体上看,方案二的误差小于方案一。方案一和方案二误差都随时效增加而增大,这与实际的预报经验一致。
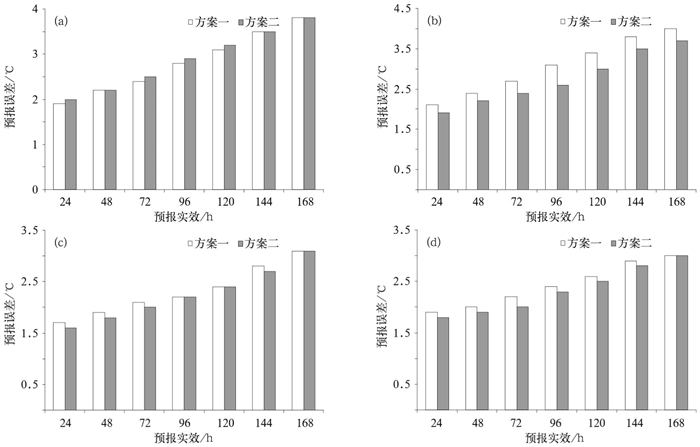
|
|
| 图 3. 2009年3—5月和9—11月最高温度和最低温度预报的平均绝对误差 (a) 3—5月最高温度预报,(b) 9—11月最高温度预报,(c) 3—5月最低温度预报,(d) 9—11月最低温度预报 Fig 3. Mean absolution error of maximum and minimum temperature forecast from March to May and that from September to November in 2009 (a) maximum temperature forecast from March to May, (b) maximum temperature forecast from September to November, (c) minimum temperature forecast from March to May, (d) minimum temperature forecast from September to November | |
4.2 平均误差对比
图 4分别给出了华北地区方案一和方案二极端温度预报平均误差。由图 4可见,方案一和方案二最高温度、最低温度7个时效的平均误差都在-1~1℃之间,部分时效的平均误差为零或者接近零,说明两个方案温度预报的系统误差都不明显,3—5月的最高、最低温度预报以偏低为主,而9—11月的预报大多偏高。方案一和方案二的预报平均误差没有通过显著性差异检验,说明两者没有明显差异。
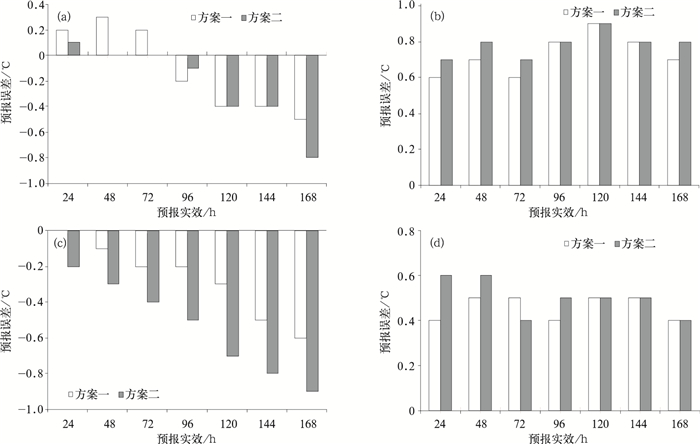
|
|
| 图 4. 2009年3—5月和9—11月最高温度和最低温度预报的平均误差 (a) 3—5月最高温度预报,(b) 9—11月最高温度预报,(c) 3—5月最低温度预报,(d) 9—11月最低温度预报 Fig 4. Average error of maximum and minimum temperature forecast from March to May and that from September to November in 2009 (a) maximum temperature forecast from March to May, (b) maximum temperature forecast from September to November, (c) minimum temperature forecast from March to May, (d) minimum temperature forecast from September to November | |
4.3 误差在2℃以内站次百分比对比
绝对误差不高于2℃站次百分比 (图 5) 显示,除了3—5月的最高温度预报中,方案二百分比值略小于方案一外,其他时段和时效都是方案二百分比值大于方案一,说明从总体上看方案二的预报效果要好于方案一。
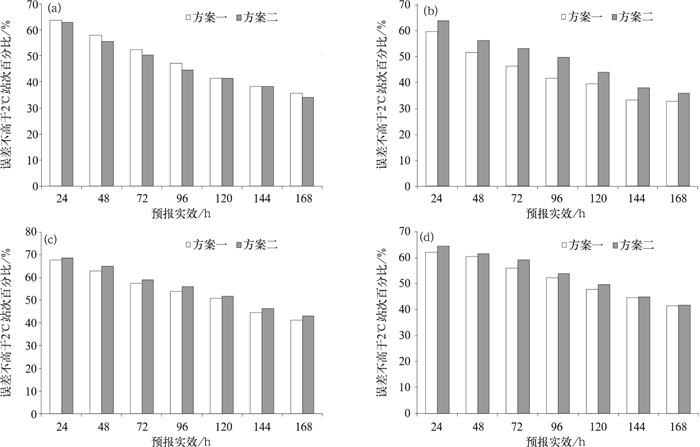
|
|
| 图 5. 2009年3—5月和9—11月最高温度和最低温度预报的绝对误差不高于2℃站次所占百分比 (a) 3—5月最高温度预报, (b) 9—11月最高温度预报, (c) 3—5月最低温度预报, (d) 9—11月最低温度预报 Fig 5. Percentage of stations with absolute error of maximum and minimum temperature forecast less than 2℃ from March to May and that from September to November in 2009 (a) maximum temperature forecast from March to May, (b) maximum temperature forecast from September to November, (c) minimum temperature forecast from March to May, (d) minimum temperature forecast from September to November | |
如果以绝对误差小于2℃的站数占总站数的百分比达到50%以上均可用的话,3—5月两种方案最高温度可用预报均达72 h,最低温度可用预报均达120 h;9—11月方案一最高温度可用预报达48 h,最低温度可用预报达96 h, 而方案二最高温度可用预报达72 h,最低温度可用预报达96 h。
5 结论和讨论通过以上分析得到如下结论:
1) 针对客观气象要素预报,在华北地区进行多次季节划分试验的基础上,提出一种新的季节划分方式,分别为早春晚秋类 (2月11日—3月10日和11月5日—12月4日)、夏季类 (5月1日—9月30日)、晚春早秋类 (3月21日—4月30日和10月1日—11月4日)、冬季类 (12月5日—2月10日)。
2) 采用新的季节划分方式,利用模式回算资料建立MOS预报方程,预报误差总体上小于传统的季节划分方式下的预报误差,预报绝对误差在2℃以内站次百分比大于传统的季节划分方式,说明新的季节划分方式更适合于温度MOS预报。
3) 两种季节划分方式预报平均误差没有明显区别,误差绝对值都不大,说明系统误差不明显。
3—5月新的季节划分方式预报误差相对于传统的季节划分方式没有下降,还略有增加,原因可能与2009年春季温度本身的变化以及聚类分析的技术方案有关,有待进行更深入的研究和改进。
本文仅是对华北地区进行季节划分试验,下一步将会拓展到全国各个区域,针对不同区域研究温度MOS预报季节划分问题,并分析不同区域季节划分的差异, 寻找合适的季节划分方式。
| [1] | 矫梅燕, 龚建东, 周兵, 等. 天气预报的业务技术进展. 应用气象学报, 2006, 17, (5): 594–601. |
| [2] | 杨成荫, 王汉杰, 周林, 等. 基于全场信息的数值预报产品释用方法研究. 应用气象学报, 2009, 20, (2): 232–239. |
| [3] | 王迎春, 刘凤辉, 张晓玲, 等. 北京地区中尺度非静力数值预报产品释用技术研究. 应用气象学报, 2002, 13, (3): 312–321. |
| [4] | Caren Marzban, Scott Sandgathe, Eugenia Kalnay. MOS, perfect prog, and reanalysis. Mon Wea Rev, 2006, 134, (2): 657–663. DOI:10.1175/MWR3088.1 |
| [5] | 江双五, 田红, 陈丽娟. 动力延伸预报产品释用方法的改进试验. 应用气象学报, 2005, 16, (6): 779–786. |
| [6] | 池俊成, 史印山. EOF迭代模型的月动力延伸预报产品释用方法. 应用气象学报, 2009, 20, (1): 124–128. |
| [7] | 吴爱敏, 郭江勇. HLAFS资料在短期降水、气温MOS预报方法中的应用. 干旱气象, 2006, 24, (2): 45–48. |
| [8] | 吴君, 裴洪芹, 石莹, 等. 基于数值预报产品的地面气温BP-MOS预报方法. 气象科学, 2007, 27, (4): 430–435. |
| [9] | 陈豫英, 陈晓光, 马金仁, 等. 基于MM5模式的精细化MOS温度预报. 干旱气象, 2005, 23, (4): 53–56. |
| [10] | 刘还珠, 赵声蓉, 陆志善, 等. 国家气象中心气象要素的客观预报-MOS系统. 应用气象学报, 2004, 15, (2): 181–191. |
| [11] | Glahn H R, Lowry D A. The use of model output statistics (MOS) in objective weather forecasting. J Appli Meteor, 1972, 11, (8): 1203–1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2 |
| [12] | Klein W H, Lewis F. Computer forecasts of maximum and minimum temperatures. Meteorological Applications, 1959, 9, (3): 350–359. |
| [13] | 李凯, 常圣领. 基于K-means聚类的神经网络分类器集成方法研究. 计算机工程与应用, 2009, 45, (22): 120–123. DOI:10.3778/j.issn.1002-8331.2009.22.039 |
| [14] | 石云平. 聚类K-means算法的应用研究. 理论与方法, 2009, 28, (8): 28–31. |
| [15] | 汤桂生, 杨克明, 王淑静, 等. 聚类分析在暴雨预报和环流形势分型中的应用. 气象, 1996, 22, (8): 33–38. DOI:10.7519/j.issn.1000-0526.1996.08.007 |
| [16] | 杞明辉, 肖子牛, 晏红明. 一种改进的考虑环流特征的MOS预报方法. 高原气象, 2003, 22, (4): 405–409. |
| [17] | 黄嘉佑. 气象统计分析与预报方法. 北京: 气象出版社, 1990. |
 2011, 22 (4): 429-436
2011, 22 (4): 429-436



