2. 北京应用气象研究所,北京 100029
2. Beijing Institute of Applied Meteorology, Beijing 100029
20~60 km高度范围大气是中层大气的重要组成部分,该层大气风场数据对于研究平流层环流和大气中各种波动等具有重要意义。然而该层大气风场直接探测手段有限,且存在一定的局限,地基观测的高度范围受到很大限制,站点分布也不均匀。卫星可以提供全球范围多种大气参数观测,但是由于测量风场的设备复杂,很多卫星都没有搭载直接测量风场的设备或者搭载的测风设备运转不正常。观测资料的相对稀少,给人们研究该层大气风场带来一定困难,因此多年来对该高度范围大气的研究很不充分。与20~60 km高度范围大气风场观测数据不同,温度场、气压场和密度场资料较丰富,而大气的温度、压强及密度和风场在一定条件下满足一定的关系,在平均状态下,可以利用大气温度、压强和密度的测量推算出大气平均风场,为此,科学家曾作了大量推算风场的工作。Andrews等[1]、Hedin等[2]提出纬向平均温度场与纬圈平均纬向风保持地转平衡的假设,认为可以从温度和压强推算出纬向平均风。对于利用温度资料计算风场的方法,也有不少人进行过探究。Fleming等[3]利用Nimbus-5和Nimbus-6的温度探测资料,采用梯度风公式计算了各纬圈上的纬向平均风。Oberheide等[4]利用1994年10月低温红外分光计和望远镜 (CRISTA) 两天的纬向平均温度数据,计算了15~90 km范围内的纬向平均地转风。在国内,马瑞平等[5]利用Nimbus-7卫星SAMS的温度数据计算了中国区域20~80 km高度的地转风,指出中国上空 (110°E)20~80 km的纬向风与CIRA 86的纬圈平均纬向风有显著差别。刘三军等[6]利用2005年Aura卫星上微波临边探测器 (MLS) 观测的压强、温度、密度数据,推算出中层大气每天的全球背景风场以及纬圈平均纬向风。但是采用其他物理量来推算风场的方法却不多见,COSMIC (Constellation Observing System for Meteorology Ionosphere and Climate) 掩星观测可独立反演大气折射指数随高度变化的廓线,辅助相应的大气信息,就可以得到丰富的大气压强、温度与密度等资料,即气压、温度和密度等信息都是建立在折射率信息的基础上获取的,大气折射指数廓线是COSMIC掩星技术的第1级反演产品,它的精度更能够反映掩星观测的精度,因此,本文拟采用COSMIC掩星大气压强与折射指数资料,试图运用梯度风方程构建计算20~60 km中层大气纬圈平均纬向风场的方法,并按照构建的方法计算出2007年1,4,7月和10月中高纬度地区的大气纬圈平均风场,与再分析风场模式资料进行了对比分析。
1 资料本文采用COSMIC掩星折射指数资料计算20~60 km中层大气风场;采用美国国家环境预报中心 (NCEP) 和美国国家大气研究中心 (NCAR) 联合制作的NCEP/NCAR再分析资料50 hPa位势高度数据作为折射指数积分位势高度时的边界条件;采用欧洲中期天气预报中心 (ECMWF) 提供的ERA-interim (ECMWF Reanalysis-interim) 以及美国国家航空航天局NASA和GMAO (NASA/Global Modeling and Assimilation Office) 提供的MERRA (Modern Era Retrospective-analysis for Research and Applications) 再分析风场资料作为对比,验证计算风场的可靠性。
1.1 COSMIC掩星资料COSMIC掩星星座是美国和中国台湾地区联合发展的气象、电离层与气候的星座观测系统,于2006年4月15日发射成功,初始轨道高度为512 km,倾角为72°。发射之后的17个月里卫星轨道逐步升高到800 km,卫星之间的升交点赤经间隔调整为30°,利用低轨卫星与GPS系列卫星配合,采用无线电掩星技术,完成大气垂直廓线的观测。该系统1天能提供约2000组的观测数据,这些数据垂直分辨率高,在平流层垂直分辨率接近1.0 km;空间覆盖范围大,垂直范围可从大约60 km高度一直到陆地或海洋的表面,水平范围可以覆盖全球,且分布近似均匀;卫星上仪器设备长期稳定,不需要在轨定标[7-8],为进行中层大气研究提供了机会。Anthes等[9]对COSMIC掩星探测资料作了初步的分析,结果表明:COSMIC资料的质量比以往的GPS掩星资料质量高。本文选用的2007年1,4,7月及10月资料是COSMIC掩星的干空气后处理资料,通过COSMIC掩星数据网站www.cosmic.ucar.edu下载,资料内容包括掩星事件的高度、纬度、经度、折射指数、温度、气压等。经过质量控制后,1,4,7月及10月的掩星观测次数分别为52963,52195,51174和36599,本文采用反距离加权插值的方法,将折射指数插值到5°×5°网格上,用于计算分析。
1.2 NCEP再分析位势高度场资料NCEP/NCAR再分析数据采用当今最先进的全球同化系统和数据库,对各种资料来源 (地面、船舶、无线电探空、气球、飞机、卫星等) 的观测资料进行质量控制和同化处理,获得了一套完整的再分析资料,包含的要素多,范围广,延伸时间长,是一个综合的观测资料集。该资料覆盖全球范围,垂直方向从近地面的1000 hPa至平流层的10 hPa (约30 km),其再分析场和预报场资料已普遍被世界各国气象部门使用,温度、压强和位势高度等再分析资料与气候分析相似度很高[10]。为便于比较分析,采用反距离加权插值的方法,将其水平网格由2.5°×2.5°插值到5°×5°网格上。本文选用的50 hPa等压面的位势高度月平均资料,下载自网站www.cdc.noaa.gov。
1.3 ECMWF再分析风场资料ECMWF再分析气象资料主要有ERA-15, ERA-40, ERA-interim等。与ERA-40相比,ERA-interim借鉴了ERA-40和JRA-25(Japanese 25-year Reanalysis) 在数据质量控制方面的经验,更好地制定背景误差约束,并改进物理模型,采用新的湿度分析,同时提供了更多的数据产品。资料同样覆盖全球范围,气压分层由ERA-40的23层增加到37层,从近地面的998 hPa至0.l hPa (约64 km)。该资料集提供变量包括了气温、纬向风速、经向风速等气象要素,还加入一些ERA-40所没有的云参数[11-12]。ECMWF资料时间序列长、垂直层次高,在平流层中使用了纯等压面坐标,资料的可信度相对时间序列长的再分析资料 (如NCEP资料) 好[13]。相对应地本文选用ERA-interim月变化风场数据,该数据水平分辨率为1.5°×1.5°,垂直方向从近地面至1 hPa (约47 km) 高空,在50~1 hPa (约20~50 km) 高度区间共包含9个层次,为了便于比较分析,仍采用反距离加权插值的方法,将其插值到5°×5°网格上。本文采用的ERA-interim再分析风场资料,均下载自网站www.ecmwf.int/products/data。
1.4 MERRA再分析风场资料MERRA再分析资料是在GEOS-5(Goddard Earth Observing System Data Assimilation System) 系统基础上,采用NCEP模式统一的格点插值方案,进行增量分析、质量控制和同化处理,获得的一套完整的再分析数据。该资料覆盖全球范围,包含温度、位势高度、纬向风速和经向风速等气象要素,与观测资料以及NCEP,ECMWF等模式比较验证,结果真实可信,同时该模式具有比以往数据分析模式具有更高的时间和空间分辨率[14-15]。为了便于比较,仍采用反距离加权插值的方法,将其插值到5°×5°网格上。本文用到的MERRA风场再分析资料,均下载自网站disc.sci.gsfc.nasa.gov/mdisc/data-holdings。
2 利用大气折射指数计算风场的方法 2.1 资料预处理方法 2.1.1 网格插值方法本文在垂直方向采用对数压力高度 (定义为z=-7ln (p/p0),其中,p0=1000 hPa)[1]标度,对每一条廓线的折射指数按三次样条函数进行插值,插值过程中确保含有50,30,20,10,7,5,3,2 hPa和1 hPa 9个等压面对应的大气折射指数月平均数据。水平方向取经度间隔5°、纬度间隔5°建立水平网格,网格点分布为:λ=5i-180, i=0, 1, ……, 71; φ=5j-85, j=1, 2, ……, 33,每一个等压面上以各水平格点为中心,确立长和宽都为10°的窗口矩形,格点 (i,j) 上的气象参数值由矩形内的测量点确定。不同测量点与窗口矩形中心的距离不同,它们接近网格点正确值的程度也不同,距离越近测量值越接近格点 (i,j) 的真实值,距离越远测量值离格点 (i,j) 真实值的差别越大。对每一高度层的各水平格点,以该格点为中心,在窗口矩形范围内,利用M=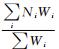
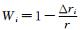
20~60 km中层大气相对比较稳定,本文认为在10 d范围12 h区间内,大气折射指数变化不大。可将1天分为00:00:00—11:59:59和12:00:00—23:59:59两个时段,再将1个月分为上旬、中旬和下旬,1个月得到6个折射指数场。每个折射指数场中的掩星观测数约6000~10000,每个格点所在的矩形窗内掩星观测数在65°~80°N,65°~80°S高纬度地区、25°~60°N,25°~60°S中纬度地区及20°N~20°S赤道低纬度区域分别约为6,13,8次,满足插值要求,图 1给出了其中一个折射指数场2007年4月上旬00:00:00—11:59:59的COSMIC掩星事件全球分布图,图中黑点代表指定时间分布在全球网格的掩星点。从COSMIC掩星观测数据中提取20~60 km大气压强及折射指数廓线数据,首先将每一次的观测放到经度、纬度和观测时段对应的网格里。由于掩星观测在两极的观测次数相对少,舍弃了包含纬度90°N,90°S和85°N,85°S网格的数据结果,本文用于计算风场的理论适用于中高纬度地区,在低纬度地区效果不佳,因此20°N至20°S以内的资料也没有计算。将廓线按三次样条函数插值到高度范围为20~60 km (约0.2~50 hPa) 对应压高层面的格点上,压高间隔为0.2 km,采用反距离加权插值的方法将同一折射指数场的折射指数数据 (即1个月内相同时段的所有廓线折射指数) 插值到全球网格上,再将不同折射指数场对应网格点的数据取几何平均,得到月平均数据用于计算风场,将1天分为两个时段再取平均是为了减小潮汐对计算得到风场的影响,选取50,30,20,10,7,5,3,2 hPa和1 hPa共9个等压面的风场资料用于比较分析。

|
|
| 图 1. 2007年4月上旬00:00:00—11:59:59 COSMIC掩星事件全球分布 Fig 1. The global distribution of radio occultation events from 00:00:00 to 11:59:59 during 1—10 April 2007 | |
2.2 风场的计算处理方法的构建 2.2.1 风场理论的选用
目前,利用大气压强、密度及温度等气象参数推算全球风场的方式主要有地转风、梯度风和平衡风等方法,在中层大气纬度较低的部分大尺度水平运动的风场满足通常的地转近似,这种近似只是水平气压梯度力与Coriolis力二者平衡,可以用地转风方程描述。在纬度较高的部分大尺度水平运动风场要采用更为精细的近似,水平气压梯度力、Coriolis力和曲率项力三者平衡,需要用梯度风描述[18]。平衡风在梯度风基础上还考虑了大气平流项的影响,但计算方程较为复杂。肖存英等[19]对由卫星温度数据计算风场的有效方法,包括地转风、梯度风、平衡风的计算方法,进行了详细分析,并指出纬圈平均平衡纬向风与梯度风基本重合,纬圈平均经向风都特别小,纬向风在本质上代表了大气环流的本质特征。鉴于上述原因,本文利用COSMIC掩星折射指数数据,选用相对简单的梯度风方程构建计算纬圈平均风场的方法。
大尺度运动满足的水平动量方程为[1]:
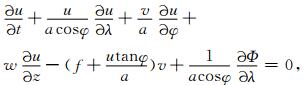
|
(1) |
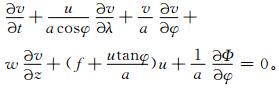
|
(2) |
其中,λ,φ,z分别为经度、纬度、气压高度;u,v,w分别为纬向风、经向风、垂直风;t为时间;Φ为位势;a为地球半径;f=2Ωsinφ,Ω=7.292×10-5s-1为地球自转角速度。在自由尺度的大气中,地转风是实际风的一个很好近似,但在靠近极地的高纬度地区,地球的曲率项不可忽略,影响较大。若忽略平流项的作用,保留曲率项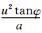
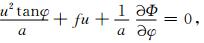
|
(3) |
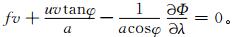
|
(4) |
通常用ugr,vgr分别表示梯度纬向风和梯度经向风,由式 (3) 可以得到解析解。对式 (3)、式 (4) 分别作纬圈平均,可以得到ugr,vgr:

|
(5) |

|
(6) |
① 读取NCEP再分析资料50 hPa等压面的月平均位势高度数据,采用反距离加权插值的方法,将其水平网格由2.5°×2.5°插值到5°×5°网格上,作为由折射指数积分位势高度时的边界。
② 在20~60 km之间大气中的水汽含量极少,可以假定为干空气,有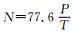

③ 在干空气假设下,对处于20~60 km的大气,利用各等压面上的COSMIC掩星折射指数数据,以50 hPa等压面的位势高度数据作为积分边界条件,采用均质大气模式,通过测高方程式 (7) 和位势定义[1]式 (8) 来计算不同等压面的位势高度:

|
(7) |
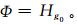
|
(8) |
其中,g0=9.80665 m/s2为平均重力加速度,R=287.05 J/(K·kg) 为干空气的气体常数,H为位势高度,N为P1与P2间气体的平均折射指数。
④ 基于计算出的位势,采用中心差分法,由梯度风公式式 (3) 计算梯度纬向风ugr,代入式 (4) 计算得到梯度经向风vgr,分别作纬圈平均,即可以得到纬圈平均纬向风和经向风ugr,vgr。
2.3 误差分析经过纬圈平均后,中层大气纬圈平均经向风风值一般都很小,纬圈平均纬向风代表了那里大气环流的本质特征,对利用COSMIC掩星数据计算的纬向平均风场误差分析,主要考察纬圈平均纬向风的偏差,参考文献[20-21]的方法,对于1~50 hPa固定等压面的风场数据,每一个纬圈利用式 (9) 来计算纬向风偏差:
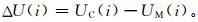
|
(9) |
式 (9) 中,UC(i),UM(i) 分别代表计算风场与再分析风场在相应格点上的纬圈平均纬向风速;ΔU(i) 为两者在对应纬圈的纬向风偏差。在每个等压面上风速的平均偏差可以由式 (10) 计算得到:
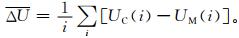
|
(10) |
式 (10) 中,ΔU为计算风场与模式风场在指定等压面的平均偏差。利用式 (11) 可以得到风场的标准偏差SΔU:
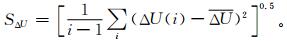
|
(11) |
采用上述构建方法,选用2007年4月和10月的COSMIC掩星折射指数计算得到全球中高纬度地区月平均纬圈平均风场,并对ECMWF资料及MERRA资料4月和10月的月平均风场分别做纬圈平均,进行对比分析。如图 2所示,分别为4月及10月COSMIC掩星折射指数数据计算获得的风场和ECMWF,MERRA再分析风场纬圈平均经向风速随纬度、高度的变化曲线。经向风通过波动在各纬圈之间进行空气交换,经过纬圈平均后,纬圈平均经向风几乎为0。根据COSMIC数据推算所得的4月纬圈平均经向风最大风速不到0.1 m/s,ECMWF及MERRA风场输出结果也显示纬圈平均经向风速很小,各纬圈的最大风速不超过0.5 m/s,计算得到的10月纬圈平均经向风速相对4月较大,但最大风速也仅为0.5 m/s左右,ECMWF及MERRA再分析风场也仅1 m/s左右。计算风场与再分析风场纬圈平均经向风速相对偏差非常大主要是两方面原因造成的,一方面梯度风方程没有考虑大气平流项的影响,而大气平流项对经向风影响较大,造成纬圈平均经向风速偏小[19];另一方面由于中层大气20~60 km纬圈平均经向风自身风值特别小,较小的偏差也会导致相对偏差显著。纬圈平均经向风相比纬向风很小,纬向风环流代表了大气环流的本质特征,下文将主要对纬圈平均纬向风进行分析讨论。

|
|
| 图 2. 4月及10月中高纬度纬圈平均经向风速随纬度、高度变化对比 (单位:m·s-1) Fig 2. Latitude-altitude cross section of zone-mean meridional winds from COSMIC, ECMWF, MERRA in April and October (unit: m·s-1) | |
首先,选取纬圈平均纬向风在80°S, 55°S, 30°S, 30°N, 55°N和80°N随高度变化的情况进行对比分析。图 3分别为4月及10月COSMIC掩星折射指数计算获得的风场和ECMWF及MERRA再分析风场在不同纬度的高度变化曲线,用UC, UE和UM表示; COSMIC掩星折射指数计算风场与再分析风场之间偏差,分别用UC-UE和UC-UM表示。4月,20~60 km南半球主要为西风,风速随高度增高增大;北半球风速整体较小,最大不到20 m/s,在高纬度地区随高度有明显的转向,由西风转为东风。南北半球偏差整体都不大,南半球基本在5 m/s以内,北半球在2 m/s以内。80°S和55°S西风逐渐增强,80°S整层计算结果都偏低,偏差在2 m/s以内,到1 hPa等压面偏差大于2 m/s,55°S在低层计算结果偏高,到高层计算结果偏低,偏差都在3 m/s以内;30°S在10 hPa等压面以下纬向风相对较弱,之后西风逐渐增强,计算结果基本都偏低,在2 hPa等压面以下偏差较小,基本在2 m/s以内,而到1 hPa等压面偏差达到最大,比模式结果低约4~5 m/s;30°N西风先增强后又减弱,两者偏差存在一个由正偏差到负偏差再到正偏差的变化;而在55°N西风先减弱后又增强,偏差先增大后减小;在80°N,西风逐渐减弱,到3 hPa等压面附近转为东风,之后东风逐渐增强,计算风随高度增大速度比模式风快,偏差也由负偏差逐渐变为正偏差。

|
|
| 图 3. 2007年4月及10月不同纬圈平均纬向风速随高度变化曲线及对应的差别 Fig 3. Height profiles of the COSMIC and model zone-mean zonal winds derived for various latitudes and the bias in April and October of 2007 | |
10月,20~60 km南、北半球高纬度地区主要为西风,低纬度地区部分高度盛行东风;南半球风速随高度增加逐渐成减小趋势,北半球则逐渐增大。南半球最大偏差5 m/s左右,沿极区到低纬度方向偏差有减小趋势。80°S和55°S西风逐渐减弱,80°S计算结果先是偏低,到高层后结果偏高,整层偏差在5 m/s以内;55°S计算结果偏高,偏差在3 m/s以内,在3 hPa等压面与MERRA偏差超过3 m/s;30°S东风随高度增加先增强,后又减弱,3 hPa后又转为西风,低层为正偏差,后转为负偏差,偏差在2 m/s以内;北半球都处于西风区,且西风随高度的增加而加强,最大风速接近40 m/s,低纬度地区计算风场结果偏大,中高纬度地区计算风结果偏小,偏差随高度增加而增大,但最大偏差不超过8 m/s。不论是4月还是10月,COSMIC掩星折射指数计算出的纬圈平均纬向风与两种再分析风场的变化规律都非常一致,能够反映大气风场的特性。
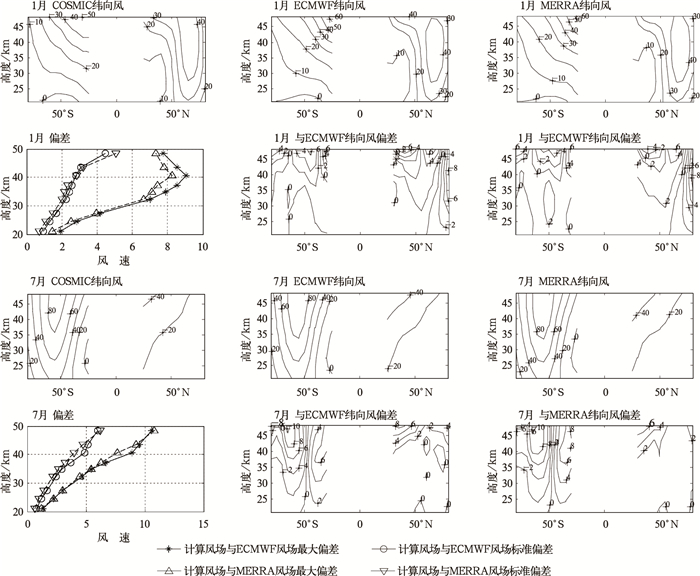
为进一步确认掩星折射指数计算风场方法的可靠性,选用2007年1月及7月COSMIC掩星资料计算风场与再分析风场对整个中高纬度地区风场随纬度高度的变化差异进行比较。图 4分别为1月及7月计算风场和ECMWF及MERRA风场在50, 30, 20, 10, 7, 5, 3, 2 hPa和1 hPa 9个等压面上纬向风随纬度、高度变化的等值线图,1月及7月计算风场与ECMWF及MERRA的偏差图。由图 4可知,COSMIC掩星资料计算风场与再分析风场等值线图形状非常相近,整体变化规律一致。2007年1月,南半球盛行东风,东风随高度增加逐渐增强,北半球盛行西风,风速沿低纬度到极区方向变化明显,西风先增强后减弱。计算风场与再分析风场偏差主要集中于高度大、纬度高的区域,标准偏差最大为5 m/s左右,最大偏差不超过9 m/s。7月风场变化规律与1月反相,南半球盛行西风,沿低纬度到极区方向西风先增强后减弱,中纬度地区风速最大,超过了80 m/s,北半球盛行东风,风速相对南半球偏小,东风随高度增加逐渐增强。计算风场与再分析风场偏差主要处于整个南半球及北半球高层区域,标准偏差比1月略大,最大约为6 m/s,最大偏差不超过11 m/s。为清晰表现出计算风场与再分析风场的整体偏差,本文还统计了1月和7月各等压面的最大偏差、标准偏差及纬圈平均纬向风沿纬度方向的相关系数,中高纬度地区的最大偏差、标准偏差都随高度增加而增大,相关系数有减小的趋势,但不低于0.98。30, 20, 10, 7, 5, 3, 2 hPa和1 hPa各等压面偏差及相关系数具体情况见表 1。
|
|
| 图 4. 2007年1月及7月纬圈平均纬向风随纬度、高度变化对比 (单位:m·s-1) Fig 4. Zone-mean zonal winds in January and July of 2007 by COSIC, ECMWF, MERRA datasets and the differences between COSMIC and reanalysis (unit:m·s-1) | |
|
|
表 1 2007年1月及7月COSMIC计算风场和再分析风场在1~30 hPa等压面的纬圈平均纬向风偏差 Table 1 The zone-mean zonal winds bias between the COSMIC and reanalysis derived for various heights from 1 to 30 hPa in January and July of 2007 |
4 结论
本文利用COSMIC掩星折射指数资料,根据大气折射指数与大气密度、风场之间的相互关系,选用梯度风方程,构建了推算20~60 km中层大气风场的方法,并按照构建方法计算了2007年1,4,7月及10月的大气纬圈平均风场,简单分析了大气纬圈平均风随纬度、高度的变化特征及规律。COSMIC掩星折射指数资料计算风场纬圈平均经向风偏小,相对偏差大,但经向风速本身小,对大气环流影响不大;纬圈平均纬向风随纬度、高度变化的特征及规律与再分析风场一致。2007年1月,南半球盛行东风,东风随高度增加逐渐增强,北半球盛行西风,沿低纬度到极区方向西风先增强后减弱。计算风场与再分析风场偏差主要集中于高度大、纬度高的区域,标准偏差最大5 m/s左右,最大偏差不超过9 m/s。7月,风场变化规律与1月反相,南半球盛行西风,沿低纬度到极区方向西风先增强后减弱,中纬度地区风速最大,超过了80 m/s,北半球盛行东风,风速相对南半球较小,随高度增加逐渐增强。计算风场与再分析风场偏差主要出现在南半球,还有北半球高层区域,标准偏差比1月略大,最大约6 m/s,最大偏差不超过11 m/s。1月及7月,中高纬度地区的标准偏差、最大偏差都随高度增加而增大,沿纬度方向相关系数有减小的趋势,但不低于0.98。4月,南半球盛行西风,风速随高度逐渐增大;北半球风速整体较小,最大不到20 m/s,在高纬度地区随高度有明显转向,由西风转为东风。风速偏差整体都不大,南半球在5 m/s以内,北半球为2 m/s以内。10月,南北半球高纬度地区盛行西风,南半球风速随高度增加逐渐呈减小趋势,北半球则逐渐增大。南半球最大偏差为5 m/s左右,沿极区到低纬度方向偏差有减小的趋势。北半球西风随高度增加而加强,最大风速接近40 m/s,低纬度地区计算风场结果偏大,中高纬度地区计算风速结果偏小,偏差随高度增加而增大,但最大偏差不超过8 m/s。
结果表明:利用COSMIC掩星折射指数资料,通过梯度风公式计算风场能够正确反映20~60 km中层大气纬圈平均风场的特性,是获取中高纬度平均风场的一种非常有效的方法,能够弥补高空风直接观测资料的不足,可以为20~60 km大气研究提供新的风场资料。
致谢 感谢CDAAC (COSMIC Data Analysis and Archive Center) 提供的COSMIC掩星数据,感谢NCEP/NCAR提供NCEP再分析场位势高度数据及ECMWF提供的ERA-interim风场资料和NASA/GMAO提供的MERRA再分析风场数据,感谢北京应用气象中心谢志辉博士对本文的建议。| [1] | Andrews D G, Holton J R, Leovy C B. Middle Atmosphere Dynamics. London: Academic Press Inc, 1987. |
| [2] | Hedin A E, Fleming E L, Manson A H, et al. Empirical wind model for the upper middleand lower atmosphere. J Atmos Solar-Terr Phys, 1996, 58: 1421–1447. DOI:10.1016/0021-9169(95)00122-0 |
| [3] | Fleming E L, Chandra S, Barnett J J, et al. Zonal mean temperature, pressure, zonal wind and geopotential height as functions of latitude. Adv Space Res, 1990, 10, (12): 11–59. DOI:10.1016/0273-1177(90)90386-E |
| [4] | Oberheide J, Hagan M E, Ward W E, et al. Modeling the diurnal tide for the Cryogenic Infrared Spectrometers and Telescopes for the Atmospheric (CRISTA)1 time periode. J Geophys Res, 2000, 105: 24917–24929. DOI:10.1029/2000JA000047 |
| [5] | 马瑞平, 廖怀哲. 中国地区20—80 km高空风的一些特征. 空间科学学报, 1999, 19, (4): 334–341. |
| [6] | 刘三军, 熊建刚, 万卫星, 等. 利用Aura卫星资料计算全球中层大气背景风场. 空间科学学报, 2007, 27, (5): 400–408. DOI:10.11728/cjss2007.05.400 |
| [7] | Kursinski E R, Hajj G A, Bertiger W L, et a1. Initial results of radio occultation observations of Earth's atmosphere using the Global Positioning System. Science, 1996, 271: 1107–1110. DOI:10.1126/science.271.5252.1107 |
| [8] | 杜明斌, 杨引明, 丁金才. COSMIC反演精度和有关特性检验. 应用气象学报, 2009, 20, (5): 586–593. |
| [9] | Anthes R A, Bernhardt P A, Chen Y, et al. The COSMIC/FORMOSAT-3 mission: Early results. Bull Amer Meteor Soc, 2008, 89: 313–333. DOI:10.1175/BAMS-89-3-313 |
| [10] | 徐影, 丁一汇, 赵宗慈. 美国NCEP/NCAR近50年全球再分析资料在我国气候变化研究中可信度的初步分析. 应用气象学报, 2001, 12, (3): 337–347. |
| [11] | http://www.ecmwf.int/research/era/do/get/ERA-Interim_brief. |
| [12] | 范晓青, 李维京, 张培群. 模式大气月尺度可预报性对比研究. 应用气象学报, 2003, 14, (1): 49–60. |
| [13] | Trenberth K E, Stepanish D P. Apthological problem with NCEP reanalysis in the stratosphere. J Climate, 2002, 16, (6): 690–695. |
| [14] | Michele Rienecker, Max Suarez, Ricardo Todling, et al. MERRA & US Reanalysis Plans & Activities. http://www.geofaculty.org:16080/reanalysis/rienecker_MERRA_(presentation).pdf. |
| [15] | Jarrett Cohen. MERRA Project to Reconstruct Last 30 Years of Earth's Climate and Weather. http://science.gsfc.nasa.gov/606/docs/newsletter/cisto_news.summer07.pdf. |
| [16] | 庄立伟, 王石立. 东北地区逐日气象要素的空间插值方法应用研究. 应用气象学报, 2003, 14, (5): 605–615. |
| [17] | 高歌, 龚乐冰, 赵珊珊, 等. 日降水量空间插值方法研究. 应用气象学报, 2007, 18, (5): 731–736. |
| [18] | 刘式达, 刘式适. 大气动力学. 北京: 北京大学出版社, 1999: 17–20. |
| [19] | 肖存英, 胡雄, 田剑华. 利用卫星温度资料计算风场的方法分析与比较. 地球物理学报, 2008, 51, (2): 325–336. |
| [20] | 徐晓华, 罗佳. COSMIC掩星折射指数廓线的统计验证. 武汉大学学报 (信息科学版), 2009, 34, (2): 214–217. |
| [21] | 蔡兆男, 王永, LiuXiong, 等. 利用探空资料验证GOME卫星臭氧数据. 应用气象学报, 2009, 20, (3): 337–345. |
 2011, 22 (3): 346-355
2011, 22 (3): 346-355



