2. 吉林省气候中心,长春 130062;
3. 国家海洋环境预报中心,北京 100081
2. Jilin Provincial Climate Center, Changchun 130062;
3. National Marine Environmental Forecasting Center, Beijing 100081
我国华南地区处于强热带季风区,雨季长,雨量多[1],其年降水量峰值出现在4—6月的前汛期和7—9月的后汛期。前汛期降水主要受大尺度西风带锋面系统影响,还与低空急流、冷空气及南支槽有关;后汛期主要是副热带高压季节性北跳之后,其南侧热带辐合带和热带气旋等热带天气系统活动形成的降水[2-3]。关于华南汛期旱涝成因的研究主要集中在青藏高原积雪、东亚季风、西太平洋副热带高压、临近海域海温、热带气旋等方面[4-13]。另外,华南汛期的水汽来源既受印度西南季风和西太平洋东南季风的影响,同时也受来自南半球越赤道气流折向而成的西南气流的影响。有关南半球环流系统,尤其是马斯克林高压和澳大利亚高压两个系统以及越赤道气流的异常对我国汛期华南降水的研究有很多,但研究结果不尽相同[14-17]。因此,还需要进行深入、细致地研究。
针对两个变量场之间的相关问题出现了新的气候统计诊断方法——多锥度方法-奇异值分解 (Multi Taper Method-Singular Value Decomposition,MTM-SVD)[18]。同小波分析相比,MTM-SVD避免了小波分析方法边界两端需要延拓及谱泄漏等局限性,MTM-SVD方法在我国气候分析中的应用成果还不多见。本文尝试使用MTM-SVD方法对华南地区汛期降水及南半球关键系统的谱特征进行分析,并与小波分析结果进行比较。在此基础上,利用MTM-SVD方法对两者的耦合场进行不同时间尺度的空间和时间重建,跟踪马斯克林高压和澳大利亚高压的时空变化对华南地区降水的影响。
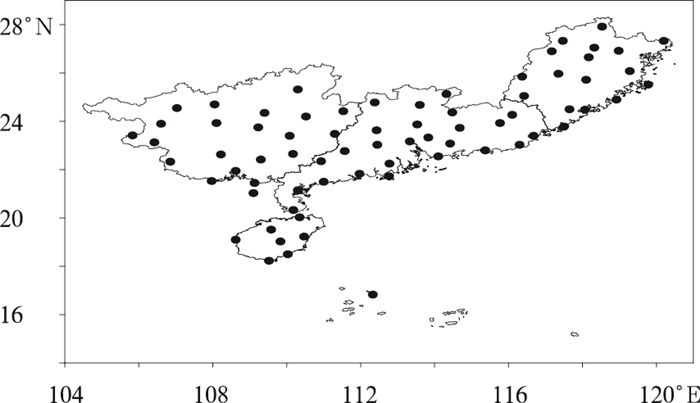
1 资料和方法 1.1 资料① 降水量资料是由国家气象信息中心提供的1960—2008年华南地区4个省 (广东、广西、福建、海南)71个测站的逐日降水量资料,其站点分布见图 1。
|
|
| 图 1. 华南地区71个站点分布 Fig 1. Distribution of 71 stations in South China | |
② 1960—2008年NCEP/NCAR南半球逐日海平面气压场 (Sea Level Pressure, SLP) 再分析资料,分辨率为2.5°×2.5°,分别选取25°~35°S,120°~150°E和25°~35°S,40°~90°E范围内的区域SLP平均值代表澳大利亚高压和马斯克林高压强度指数[16]。
1.2 分析方法和步骤 1.2.1 小波分析小波分析 (Wavelet Analysis)[19-20]是将不同波长的振幅一目了然地展现的时域结构分析方法。小波分析方法通过小波基的伸缩和平移,实现了信号的时频分析局部化,同时保留信号时域特征和频域特征,本文采用墨西哥帽小波。
1.2.2 MTM-SVD方法多锥度方法-奇异值分解是由Mann和Park发展的一种多变量频域分解技术[21-25]。它是一种将谱分析的多锥度方法 (MTM) 和奇异值分解 (SVD) 方法相结合的气候信号检测技术[26-28]。其主要特点包括:可以非常便利地分析气候变量场整体所具有的谱特征;可以为变量场重建时空信号,同时,时间模态的振幅和位相信息可以描述信号变化的包迹随时间的变化特征;可以非常方便地应用到两个变量场的耦合特征分析上,即在同一时刻多于一个的区域的耦合。对耦合场进行空间和时间的重建,可以得到几个变量场在空间及时间上的相关关系。
首先计算M个空间区域上长度为N的时间序列Ψm(t) 的标准化时间序列,m=1,…,M;再确定一列S个正交Slepian锥度as(t),同时相关的S个锥度的傅立叶变换或特征谱Ys(f)(s=1,…,S):
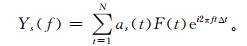
|
(1) |
式 (1) 中,F(t)(t=1,…,N) 是时间序列;Δt是样本间隔 (日、月、季、年等等)。将M个时间序列和每个频率f处的S个特征谱Yms(f)组成M×S阶的矩阵Y(f)。
在每个矩阵Y(f0) 上计算一个复数的奇异值分解,同时得到矩阵U(f0),Γ(f0) 和V+(f0):
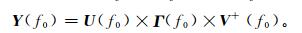
|
(2) |
式 (2) 中,Γ(f0) 是M×S阶且对角线上为奇异值γ(f0) 的矩阵;M×M阶矩阵U(f0) 的列向量是矩阵Y(f0) 的左奇异向量;S×S阶矩阵V+(f0) 的行向量是矩阵Y(f0) 的右奇异向量;V+(f0) 的有效维数是K×S。每一个主调制Vsk描述了通过调制第k个模态的振动信号的振幅和相位而产生的S个Slepian锥度影射的线性组合。利用等式Fm(t)=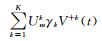
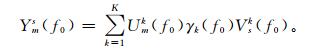
|
(3) |
式 (3) 中,K个奇异值γk(f) 按比例确定此局部分解中各个模态的振幅,并与第k个模态局部 (频率f附近窄频波段范围之内) 解释的方差百分比成正比。由第1个 (最大) 奇异值解释的局部方差百分比为
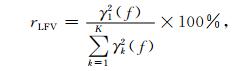
|
(4) |
rLFV提供了一个频域的局部信号检测参数。利用式 (4),由第1模态说明的rLFV可被视为一个频率函数,它产生了一个类似于谱的图,称之为LFV谱。rLFV谱的频率解析度在±fR和±pfR之间变化,其中fR为频率,p为波段宽度参数。rLFV谱的显著性水平由一个独立过程确定。
长度为M的复数向量Um1(f0) 是对应于频率f0处分解的第1模态的空间EOF。它代表信号在频率f0处的空间模式,同时包含了多元数据组在所有位置m上相关的信号的位相和振幅的信息。为了说明原始数据的转换标准而重新调整Um1(f0) 的值,可以重新获得带有正确的单位的第1模态信号的空间模式分量
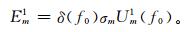
|
(5) |
其中,σm为标准差。当频率f0 ≥ pfR时选取要素δ(f0)=2来解释在频率f0和-f0处的谱信息的贡献,当0 ≤ f0 ≤ pfR时,取δ(f0)=1(长波段)。Em1中的复数值描述了在频率f0处一个振动的EOF空间模式的演变,可以用矢量形式表示,矢量的大小表示相关的振幅,角度表示位置m中的相关位相。
长度为S的复数向量分量Vs1(f0) 是对应于频率f0处分解的第1模态的谱EOF,由这个向量可以得到频率f0处信号的时间模式。信号的时间模式A1(t) 可被描述为频率f0处的主要振动,在比振动时间1/f0更长的时间范围内有振幅和相位的改变,形式为
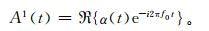
|
(6) |
式 (6) 中,可变振幅α(t) 表示振动信号的缓慢变化的包迹。时间区域A1(t) 中的信号和包迹ℜ{α(t)}形式上与频率f0处的模态相同,即变化或趋势的长期模式。
最简单的重建是Slepian锥度as(t),s=1,…,S, t=1,…,N的形式
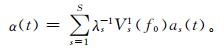
|
(7) |
式 (7) 中,Vs1(f0) 是第1模态谱EOF的第s个分量,λs是对应于第s个Slepian特征锥度的特征值。特征值λs用来测量特征锥度as的谱泄漏阻力。λs~1的特征锥度可用来构建阻止谱泄漏的谱估计。
这样可以为所有时间和区域重建时空信号Fm1(t)(其中指数1表示其与第1模态相关的信号的重建),作为这些空间和时间模式的结果,与传统的EOF一样:
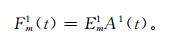
|
(8) |
分别用式 (5) 和式 (6) 中的表达式代替Em1和A1(t) 可以得到
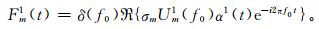
|
(9) |
这种在频率f0处分解的第1模态的相关信号的重建,可用来通过一种比分别介绍空间和时间模式更为直观的方式描述振动模式。时间变化的振幅和位相信息可通过描述相应于1个周期内多个相位Ψ(t)=2πf0t的信号的真值模式 (图) 的顺序更实际地获得。例如,重建信号的空间模式 (图) 的顺序可由覆盖全部振动的Ψ(t)=0°,90°,180°,270°,360°的那些时刻t来显示。Ψ(t)=0°和Ψ(t)=360°的图相同,图的这种顺序描述了时间1/f0的平均或典型周期内信号的变化。
1.2.3 消除指数季节变化对1960—2008年4月1日—9月30日的逐日华南地区各站降水量、马斯克林和澳大利亚区域各格点SLP做消除季节变化处理。
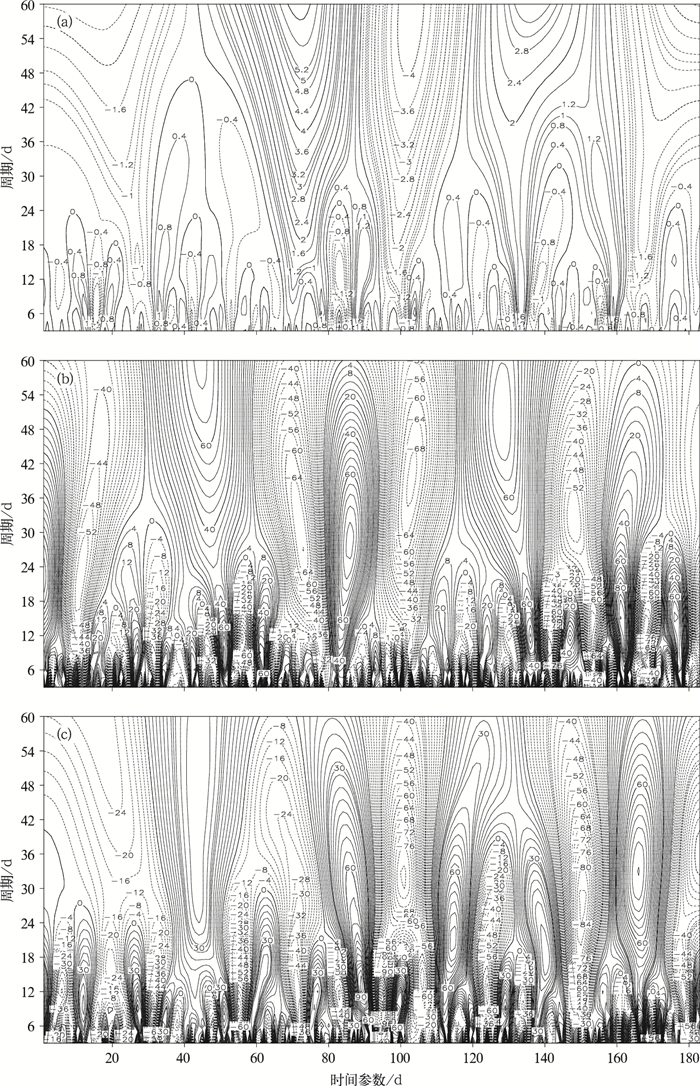
2 华南汛期降水及南半球关键系统的小波分析图 2为华南汛期降水量、马斯克林高压、澳大利亚高压序列的小波变换平面图,横坐标为时间参数,纵坐标为频率参数,图中的数值为小波系数。由图 2a对应的华南汛期降水周期变化来看,华南汛期降水具有30~60 d的低频变化特征,主要经历5个变化阶段,即前汛期开始的前40 d左右 (4月1日—5月10日) 降水偏少期、41~90 d (5月21日—6月30日) 降水偏多期、91~120 d (7月1—30日) 降水偏少期、121~160 d (7月30日—9月7日) 降水偏多期以及161~183 d (9月8—30日) 降水偏少期。由图 2b可以看出,4—9月的澳大利亚高压大致经历4个强弱交替的变化周期,即4月 (1~30 d) 的偏弱期和5月 (31~60 d) 的偏强期;6月上旬 (60~80 d) 的由偏弱期转到6月下旬 (81~90 d) 的偏强期;7月上旬高压强度 (91~110 d) 偏弱转到8月上旬 (111~140 d) 偏强;8月下旬 (141~155 d) 的澳大利亚高压偏弱期到9月又有所增强 (156~180 d)。另外,由小波系数的正负中心变化情况来看,澳大利亚高压在30~60 d左右存在中心,说明澳大利亚高压具有30~60 d左右的低频振荡特征。由图 2c可以看出,4—9月的马斯克林高压大致也经历4个强弱交替的变化周期,即4月 (1~30 d) 的偏弱期和5月中上旬 (31~50 d) 的偏强期;5月下旬和6月上半月 (51~75 d) 的由偏弱期转到6月下半月 (76~90 d) 的偏强期;7月上旬高压强度 (91~110 d) 偏弱转到8月上旬 (111~140 d) 偏强;8月下旬 (141~155 d) 的马斯克林高压偏弱期到9月又有所增强 (156~170 d)。马斯克林高压的后两个强弱变化周期时间同澳大利亚高压的强弱变化有很好的对应,说明在华南后汛期,马斯克林高压和澳大利亚高压间有很密切的关系。另外,由小波系数的正负中心看出,马斯克林高压30 d左右和12 d的振荡显著。
|
|
| 图 2. 华南汛期降水序列 (a)、澳大利亚高压强度 (b) 和马斯克林高压强度 (c) 小波变换 Fig 2. Wavelet transform of precipitation during raining season in South China (a) with SLP of the Australian high (b) and the Mascarene high (c) | |
3 华南汛期降水及南半球关键系统的LFV谱分析
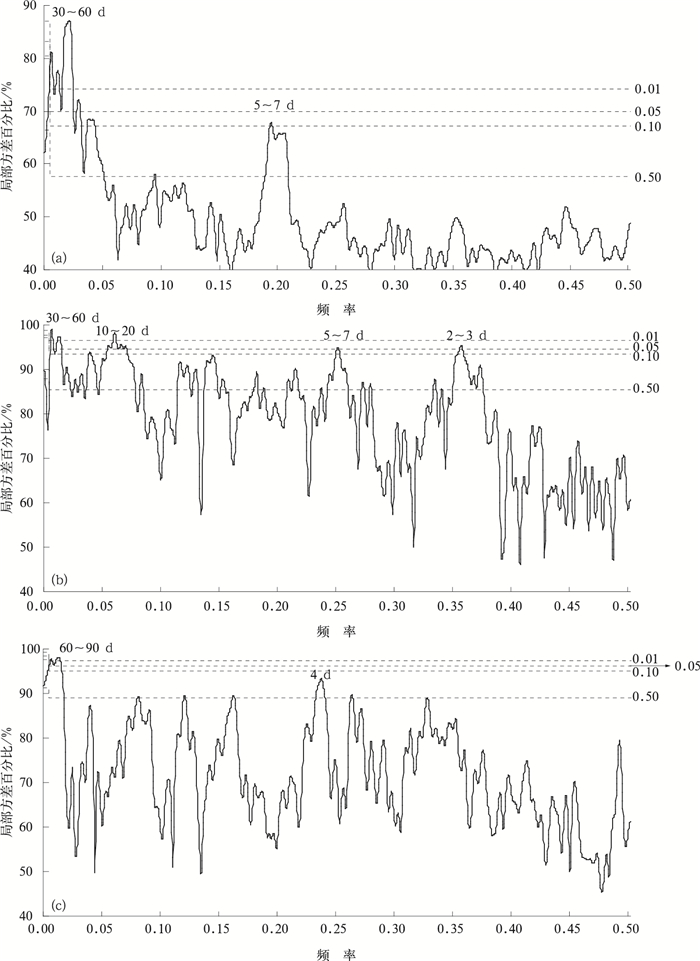
MTM-SVD方法分析华南汛期降水使用的是华南地区71个站1960—2008年平均的4月1日—9月30日的逐日降水量场资料,分析马斯克林高压和澳大利亚高压分别使用的是南半球25°~35°S,40°~90°E范围内105个格点和25°~35°S,120°~150°E范围内65个格点1960—2008年平均的4月1日—9月30日的逐日SLP场资料,样本数均为183。得到上述3个序列的第1模态局部方差百分比,局部方差百分比可被视为一个频率函数,LFV谱中,一个给定频率处的波峰预示着数据序列中在此频率处的振荡存在潜在重要的时空信号,同时也确定了LFV谱在该频率处具有统计意义的0.50,0.10,0.05,0.01的显著性水平。
由图 3a可以看出,华南汛期降水存在两个明显的峰值,其中30~60 d低频振荡的信号峰值达到0.05显著性水平,5~7 d天气过程的信号峰值达到0.10显著性水平。由图 3b可以看出, 澳大利亚高压表现出不同频率的显著振荡,其中30~60 d低频振荡和10~20 d双周振荡峰值达到0.01显著性水平,5~7 d和2~3 d天气过程的信号峰值也达到0.05显著性水平。由图 3c可以看出,马斯克林高压各种尺度的周期振荡没有澳大利亚高压明显。在不同频率处的振荡强度有明显差异,其中60~90 d低频振荡的峰值达到0.01显著性水平,其他周期的信号峰值基本没有达到0.10的显著性水平。
|
|
| 图 3. 华南汛期降水 (a)、澳大利亚高压 (b) 和马斯克林高压 (c) 的LFV谱 (虚线分别代表 0.01, 0.05, 0.10和0.50显著性水平) Fig 3. The LFV spectrum of precipitation during raining season in South China (a) with SLP of the Australian high (b) and the Mascarene high (c) (dashed lines represent the 0.01, 0.05, 0.10, 0.50 significant levels) | |
从以上分析可以看出,MTM-SVD方法不仅分析出华南降水30~60 d的低频振荡,也获得小波分析没有分析出的5~7 d周期;MTM-SVD方法分析南半球环流系统时,也分析出澳大利亚高压的5~7 d周期和马斯克林高压60~90 d周期、3~5 d周期。比较MTM-SVD方法和小波分析对华南降水和南半球关键系统的不同时间尺度的分析可知,MTM-SVD方法比小波分析得到更高的周期分辨率。
4 跟踪华南汛期降水与南半球关键系统低频变化根据华南汛期降水的低频变化特征以及对华南汛期降水影响明显的两个系统马斯克林高压和澳大利亚高压的位置,选取了南半球 (20°~40°S,35°~155°E范围内)4月1日—9月30日标准化后的SLP与华南地区降水量分别进行30~60 d (取45 d) 低频分量的空间和时间重建,从而提取影响华南降水异常低频尺度的信号。对信号在一个完整的振动周期里的空间演变过程进行重建,可以得到两个相关变量场典型的空间分布结构的演变过程,同时获得两个相关变量场的时间演变特征,从而检测两个相关变量场异常信号的空间位置以及信号的相关关系。
对华南汛期降水量和南半球SLP的耦合场在0°,45°,90°,135°,180°,225°,270°,315°,360°共9个位相处的空间模态进行重建,每个位相处的空间模态都代表了在这一时刻信号的空间分布结构的平均模态。因此,这9个位相代表了信号在一个完整的振动周期里滞后相同时间间隔处的空间演变特征,其中信号在0°位相的空间分布模态由变量场平均的最大正、负距平值确定,360°位相的空间分布结构是与初始模态相同的[18]。图 4是重建的南半球SLP场和华南汛期降水量的45 d时间尺度上的空间模态演变过程,分别为南半球SLP场和降水量位相取0°,45°,90°,135°,180°,225°,270°,315°,360°的空间分布模态,时间间隔约为5.6 d。

|
|
| 图 4. 南半球SLP场和华南地区汛期降水45 d时间尺度耦合空间重建 Fig 4. Spatial reconstruction of the joint SLP of the Southern Hemisphere and precipitation during raining season in South China at 45-day timescale | |
如图 4中南半球SLP场空间分布模态所示,在0°位相时,南半球马斯克林高压为明显的正距平区,澳大利亚高压北部地区为弱的正距平区;滞后5~6 d的45°位相时,马斯克林高压和澳大利亚高压地区的正距平强度均减弱,一直持续到90°位相时,两个高压区的正距平趋势减弱到不明显;135°位相时,马斯克林高压和澳大利亚地区转为弱的负距平控制;180°位相时,马斯克林高压的负距平更加明显,范围也扩大;225°位相时,马斯克林高压和澳大利亚高压的SLP负距平区强度开始减弱;270°位相时,两个高压区的负距平减弱为不明显状态;315°位相时,两个高压区的SLP加强为弱的正距平并持续加强到360°位相,分布模态与0°位相时相同。表明南半球马斯克林高压SLP变化的一个周期过程。
由图 4中重建得到相关的华南汛期降水同期空间分布模态可以看出,0°位相时,华南北部降水为负距平,西部和南部沿海降水量为正距平;45°位相时,华南北部降水的负距平强度略有减弱,西部和南部沿海降水的正距平也有减弱趋势;90°位相时,华南中西部大部分地区的降水均为弱的正距平,东部的福建为弱的负距平控制。135°位相时,华南地区北部降水为正距平,西部和南部沿海为负距平,180°位相北部降水的正距平、西部和南部沿海降水的负距平更加明显;225°位相时,距平值又开始减小,同135°位相时的分布类似,持续减小到270°位相时,华南的广东和广西降水量为负距平,福建和海南为正距平,但正负距平均不明显。315°位相时,降水量距平分布同45°位相时类似,华南北部降水量为负距平,西部和南部沿海为正距平,距平加强到360°位相时,回到0°位相时的分布,表明南部和北部雨带降水量的一个循环交替。
从两个相关场45 d的空间演变过程可以看出:华南地区的降水分布与南半球马斯克林高压和澳大利亚高压的SLP场变化有密切关系。南半球SLP演变过程同华南降水分布形式关系密切。南半球马斯克林高压和澳大利亚高压的SLP场由强到弱的演变过程对应华南地区降水的多雨带由西南向东北的转移;而南半球马斯克林高压和澳大利亚高压的SLP场由弱到强的演变过程对应华南地区降水的多雨带由东北向西南的转移。
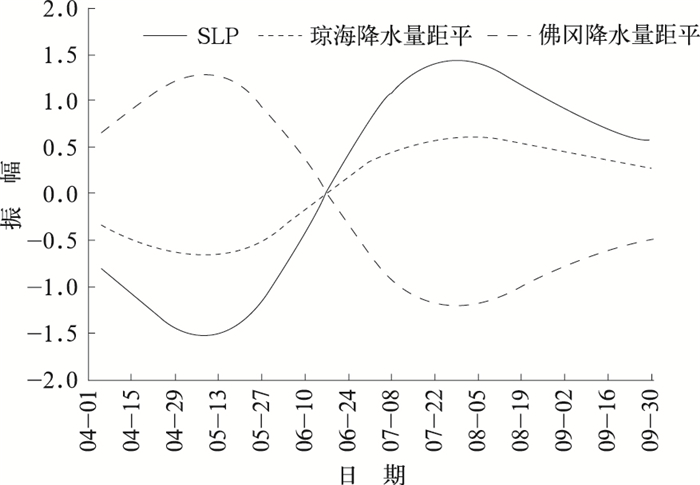
以南半球马斯克林高压附近的SLP为中心对45 d周期的重建,以海南的琼海代表华南地区南部雨带,以广东的佛冈代表华南地区北部雨带,三者随时间变化反应了南半球SLP场和华南地区南、北雨带的关系。图 5是华南地区汛期降水和南半球SLP场的长期趋势变化的时间重建。由三者长期变化趋势可见,南半球SLP场在6月中旬前后发生明显的突变,由SLP负距平转为正距平,伴随着SLP的突变,华南地区南部雨带 (琼海) 降水也开始由前汛期的少雨时段突变到后汛期多雨时段,而华南地区北部雨带 (佛冈) 则由前汛期偏多雨时段突变到后汛期的少雨时段。从长期变化趋势来看,以琼海为代表的华南地区南部雨带的降水变化同南半球SLP场变化趋势和位相保持一致,而以佛冈为代表的华南地区北部雨带则与南半球SLP场的变化趋势相反。这说明,南半球SLP场和华南地区南部雨带有很好的正相关关系,而与华南地区北部雨带为明显的负相关关系,即当南半球马斯克林高压和澳大利亚高压的SLP为正距平时,华南南部雨带为多雨时段,华南北部雨带为少雨时段,反之亦然。
|
|
| 图 5. 南半球SLP场和华南汛期降水的45 d长期趋势变化重建 Fig 5. Temporal reconstruction of the joint SLP of Southern Hemisphere and precipitation during raining season in South China at 45-day timescale | |
5 小结
1) MTM-SVD的LFV谱结果显示:华南汛期降水具有30~60 d低频振荡和5~7 d的变化特征;南半球澳大利亚高压系统具有30~60 d低频振荡、10~20 d双周振荡及5~7 d和2~3 d的变化特征;马斯克林高压系统则具有30~90 d低频振荡和双周振荡特征。
2) 跟踪华南汛期降水和南半球SLP场的30~60 d低频振荡时空耦合演变发现,南半球马斯克林高压和澳大利亚高压的SLP由强到弱的演变过程对应华南汛期降水的多雨带由西南向东北的转移;由弱到强的演变过程对应华南汛期降水的多雨带由东北向西南的转移。从长期变化趋势来看,华南地区南部雨带的降水变化与马斯克林高压和澳大利亚高压SLP场变化趋势和位相保持一致,而华南地区北部雨带则与马斯克林高压和澳大利亚高压SLP场的变化趋势相反。即当南半球马斯克林高压和澳大利亚高压的SLP为正距平时,华南地区南部易多雨,华南地区北部易少雨,反之亦然。
| [1] | 鹿世瑾. 华南气候. 北京: 气象出版社, 1990. |
| [2] | 吴尚森, 梁建茵. 华南前汛期旱涝时空分布特征. 热带气象, 1992, 8, (1): 87–92. |
| [3] | 吴尚森, 黄成昌, 薛惠娴. 华南后汛期降水的年际变化. 热带气象, 1990, 6, (4): 348–356. |
| [4] | 陈庭烈. 青藏高原冬春季异常雪盖与江南前汛期降水关系的检验和应用. 应用气象学报, 1998, 8, (增刊): 1–8. |
| [5] | 马慧, 王谦谦, 陈桢华. 华南前汛期降水异常的时空分布特征. 高原气象, 2006, 25, (2): 325–329. |
| [6] | 何有海, 关翠华, 林锡贵. 华南后汛期降雨量的振动和分布. 热带气象学报, 1998, 14, (4): 359–363. |
| [7] | 蔡学湛. 青藏高原雪盖与东亚季风异常对华南前汛期降水的影响. 应用气象学报, 2001, 12, (3): 358–366. |
| [8] | 邓立平, 王谦谦. 华南前汛期 (4—6) 月降水异常特征及其与我国近海海温的关系. 热带气象学报, 2002, 18, (1): 45–55. |
| [9] | 丁伟钰, 梁经萍. 南海地区OLR变化与华南汛期降水的联系. 热带气象学报, 2002, 18, (3): 276–282. |
| [10] | 蔡学湛, 王岩, 许金镜. 热带对流活动异常对华南前汛期旱涝影响的诊断分析. 热带气象学报, 2002, 18, (2): 157–164. |
| [11] | 鲍媛媛, 金荣花, 琚建华, 等. 2005年初夏亚洲季风异常及对华南强降雨影响. 应用气象学报, 2009, 20, (3): 276–285. |
| [12] | 谢炯光, 纪忠萍, 谷德军, 等. 广东省前汛期连续暴雨的气候背景及中期环流特征. 应用气象学报, 2006, 17, (3): 354–362. |
| [13] | 曾琮, 胡斯团, 粱建茵, 等. 东亚冬季风异常与广东前汛期旱涝关系的初步分析. 应用气象学报, 2005, 15, (5): 645–654. |
| [14] | 张婷, 魏凤英. 华南地区汛期极端降水的概率分布特征. 气象学报, 2009, 67, (3): 442–451. DOI:10.11676/qxxb2009.044 |
| [15] | 薛峰, 林一骅, 曾庆存. 论大气环流的季节气候平均情况. 大气科学, 2002, 26, (3): 308–314. |
| [16] | 何敏, 孙林海, 艾婉秀. 南半球环流异常与我国夏季旱涝分布关系及其影响机制. 应用气象学报, 2006, 17, (4): 394–402. |
| [17] | 薛峰, 王会军, 何金海. 马斯克林高压与澳大利亚高压的年际变化及其对东亚夏季风降水的影响. 科学通报, 2003, 48, (3): 287–291. |
| [18] | 韩雪.气候信号检测新方法在长江中下游降水异常变化分析中的应用.北京:中国气象科学研究院, 2006. |
| [19] | 崔锦秦, 程正兴, 译. 小波分析导论. 西安: 西安交通大学出版社, 1994. |
| [20] | 秦前清, 杨宗凯. 实用小波分析. 西安: 西安电子科技大学出版社, 1994. |
| [21] | Mann M E, Park J. Global-scale modes of surface temperature variability on interannual to century timescales. J Geophys Res, 1994, 99: 25819–25833. DOI:10.1029/94JD02396 |
| [22] | Mann M E, Park J. Joint spatio-temporal modes of surface temperature and sea level pressure variability in the Northern Hemisphere during the last century. J Climate, 1996, 9: 2137–2162. DOI:10.1175/1520-0442(1996)009<2137:JSMOST>2.0.CO;2 |
| [23] | Mann M E, Park J. Oscillatory spatiotemporal signal detection in climate studies: A multiple-taper spectral domain approach. Adv Geophys, 1999, 41: 1–131. DOI:10.1016/S0065-2687(08)60026-6 |
| [24] | Thomson D J. Spectrum estimation and harmonic analysis. IEEE Proc, 1982, 70: 1055–1160. DOI:10.1109/PROC.1982.12433 |
| [25] | Efron B. The Jackknife, the Bootstrap and Other Resampling Plans. Society for Applied and Industrial Mathematics, Philadelphia, 1990: 1-92. |
| [26] | Rajagopalan B, Mann M E, Lall U. A multivariate frequency-domain approach to long-lead climatic forecasting. Wea Forecasting, 1998, 13: 58–74. DOI:10.1175/1520-0434(1998)013<0058:AMFDAT>2.0.CO;2 |
| [27] | 魏凤英. 现代气候统计诊断与预测技术. (第二版). 北京: 气象出版社, 2007: 191–204. |
| [28] | Han Xue, Wei Fengying, Yves M Tourre. Spatio-temporal variability of Northern Hemipheric sea level pressure (SLP) and precipitation over the mid-to-low reaches of the Yangtze River. Adv Atmos Sci, 2008, 25, (3): 458–466. DOI:10.1007/s00376-008-0458-x |
 2011, 22 (3): 265-274
2011, 22 (3): 265-274



