2. 中国气象局数值预报中心,北京 100081
2. Numerical Weather Prediction Center, China Meteorological Administration, Beijing 100081
20世纪50年代,叶笃正等就指出不仅大尺度地形对东亚大气环流和我国天气有重要影响,中小尺度地形对我国天气和气候也有显著影响[1-3],后来的研究工作[4-5]更进一步支持了这一科学观点。中小尺度地形在热力和动力方面对实际大气有着不可忽略的作用,一般而言其动力作用主要包括:地形湍流拖曳力、地形阻挡及其相关效应拖曳力和地形重力波拖曳力。Davies等指出,一些无法准确描述的相对较小尺度的实际地形应该被滤掉[6],从而得到模式有效地形,而被滤掉的地形被称为次网格尺度地形,其效应只能通过参数化技术来考虑。由于数值模式分辨率的不断提高,由较小尺度地形引起的地形湍流拖曳力越来越凸显其重要性。
关于地形湍流拖曳力的研究在理论、数值模拟和参数化方法等方面取得了诸多进展。20世纪70年代至90年代,国外已在理论上对地形湍流拖曳力进行了一系列研究[7-12],并指出其产生机制为无分背风作用 (non-separated sheltering)[10]。以上理论还指出地形湍流拖曳力随着气流稳定度的加强而加强,一系列数值模拟也证实了这一点[13-16]。地形湍流拖曳力的性质和作用可概括为以下几点:① 地形湍流拖曳力直接与湍流活动有关,其必与风的切变、地面粗糙度和稳定度有关;地形湍流拖曳力是地形起伏造成的,与地形特征有关,渐近理论和数值模拟得出了地形湍流拖曳力与地形坡度的平方成正比;② 地形湍流拖曳力的方向与山脊垂直且由背风坡指向迎风坡,与风向没有关系 (只存在正负号关系);③ 地形湍流拖曳力局限在边界层某厚度范围内,有一定的衰减厚度;④ 地形湍流拖曳力可在近地层对垂直于山脊的风分量起拖曳作用,而使风偏向于山脊走向,该偏转作用一方面是因为拖曳力方向和风速存在交角,另一方面是拖曳本身可以使得风更加偏向于低压;⑤ 地形湍流拖曳力和其他过程存在相互作用,比如垂直扩散过程和其他物理过程和动力过程等。
以往模式中应用有效粗糙度法[17-19]来考虑地形湍流拖曳力,该方法认为在中性条件下,湍流气流流经起伏地形在一定垂直范围内仍然遵循对数率,然而粗糙度被增强了,称为有效粗糙度z0eff。数值试验[11, 20]和一系列观测[16, 21-24]发现并证实在地形起伏区域某高度以上,风廓线近似遵循对数率。该方法虽然不失其合理性,但同时也有一些不足之处,除了没有从理论上得到证实之外,还有以下缺点:其一,有一些地方有效粗糙度会很大,造成局地极低的虚假风速;其二,动力粗糙度增强了,可是热力和水汽粗糙度不能以同种方式增加,造成混乱;其三,这种非直接参数化方式无法研究各个参数化方案之间的动量平衡和相互作用关系。自从Wood等[13](以下简称WBH01方案) 提出直接对地形湍流拖曳力进行参数化以来,Rontu[25]将一个地形湍流拖曳力参数化方案 (简化近似WBH01的方案) 加入到高分辨有限区域模式 (HIRLAM) 中;Beljaars等[26](以下简称BBW04方案) 利用地形波谱简化了文献[11]的方案,并结合WBH01的垂直衰减方案得到了应用于欧洲中心中期天气预报模式 (ECMWF) 中的参数化方案。
尽管有关地形湍流拖曳力的研究在国际上较为成熟,然而在国内仍未开展。同时,我国幅员辽阔,地形复杂,中小尺度地形对大气的作用更为重要。本文估计了我国的4个区域 (青藏高原东部、青藏高原西部、华南地区和华中地区) 的小尺度地形平均地形标准差,并且应用BBW04方案估算了对10 m风造成的拖曳加速度。假定10 m风为10 m·s-1的平直西风,小尺度地形对10 m风的拖曳加速度的区域平均在青藏高原西部和青藏高原东部可达10-1 m·s-2,而在华南和华中地区也可达10-2 m·s-2。本文还应用BBW04方案对青藏高原东部一块区域估计了拖曳加速度的区域分布 (图略),小尺度地形在某些区域对10 m风可造成1 m·s-2以上的拖曳加速度。除了上述4个区域,我国还有大面积的地形起伏区域,由于起伏地形的大面积存在及其对低层气流拖曳的重要性,而其效应在GRAPES模式中并未考虑,本文的目的正是在研究地形湍流拖曳力作用的基础上,在GRAPES模式中考虑其作用以期对模式预报能力进行改进。
1 地形湍流拖曳力参数化方案简介基于起伏地形以上边界层平均风廓线在中性条件下近似遵循对数率,在复杂地形处采用增加地表粗糙度的方法以在模式中表述地形湍流拖曳力,这种做法称作有效粗糙度法。考虑总地面应力Ftot=Fp+Ft,其中Fp和Ft分别是地形湍流拖曳力和地面摩擦力,即

|
(1) |
式 (1) 中,ueff*是有效摩擦速度,u0*是局地摩擦速度,Fp的表达式为

|
(2) |
根据对数率关系有下式

|
(3) |
式 (3) 中,u是平均速度,κ是冯卡曼常数,z是距离平均地面的高度,z0eff是有效粗糙度。假定在高度为hm处过山气流速度未被扰动[11],即
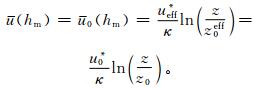
|
(4) |
如此,根据式 (1)、式 (2) 和式 (4) 就可以计算得到z0eff,对流场下边界进行强迫便可以实现参数化的目的。
WBH01结合理论和数值模拟提出了对地形湍流拖曳力进行直接参数化的方法,即将地表总应力分解为摩擦应力和地形湍流拖曳力

|
(5) |
式 (5) 中,τ130为表面摩擦应力,可以用不同方案进行闭合;Δτsso为地形湍流拖曳力,其表达式为
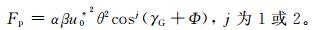
|
(6) |
式 (6) 中,α是与平均流切变有关的参数,β是与山体各向异性有关的参数,θ是地形的最大坡度,γG是中层高度处 (hm) 风矢量与山脊法向的夹角,Φ是中层到地表风旋转的角度。在垂直方向按照指数衰减,即
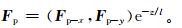
|
(7) |
式 (7) 中,l(=min (λ/π, zi/3)) 是垂直衰减尺度, λ和zi分别是山的宽度和边界层的高度。
BBW04应用美国地质调查局的3″分辨率的地形资料进行统计分析,得出小尺度地形起伏可近似认为是各向同性的结论。本文以青藏高原上30°~35°N,80°~85°E区域为例,对30″分辨率地形滤掉2 km以下和10 km以上尺度的地形求坡度 (正切) 得到与BBW04一致的结论。尽管在WBH01中将起伏地形看作为各向异性的椭圆形地形是比较理想的模型,然而在实际天气模式和气候模式中,由于实际地形的多尺度性和复杂性,考虑各向异性等参数来参数化地形拖曳力将变得异常复杂。
BBW04结合文献[11]的拖曳力表达式和文献[13]的指数衰减率,分别应用谱的形式表示地形坡度和衰减尺度,在一定假设基础上经过理论化简和模式调整,得到了以下小尺度地形湍流拖曳力参数化方案

|
(8) |
其中,α=12,β=1(物理意义同于WBH01方案),Cmd=0.005,Ccorr=0.6,分别称作拖曳力系数和矫正参数,v(z) 是水平风矢量,a2=a1k1n1-n2,a1=σflt2·(IHkfltn1)-1,σflt2为滤波后小尺度地形高度方差,对30″分辨率地形资料滤波后可得该参数的分布,IH=0.00102 m-1, kflt=0.00035 m-1,n1=-1.9,n2=-2.8。
2 一维模式及其对地形湍流拖曳力的模拟为了进一步探讨地形湍流拖曳力的特性及其影响,设计了一维模式 (单柱模式) 来模拟地形湍流拖曳力:首先比较了有效粗糙度法和直接参数化法的优劣,其次比较了针对理想地形的WBH01方案和针对实际地形的BBW04方案的各自特点。
本文所用的单柱模式包含了一组艾克曼方程 (BBW04),假定密度为1,未考虑平流项和垂直项的影响;模式由地转风驱动,地转风为垂直于山脊的纬向风,大小设为10 m·s-1,地转参数设为104s-1,用显式计算得出;垂直扩散项在中性条件下应用了一个简单的混合长理论闭合方案[27],并用隐式计算得出[28];假定地形起伏为余弦型,地形湍流拖曳力选WBH01方案时用显式算出,地形参数为解析值,选BBW04方案时用前一时刻的值,用新时刻的值,地形参数按照水平分辨率为1 km的离散点计算得出。
垂直分层由高到低逐渐变密,模式初始场在艾克曼层取对数风廓线,自由大气取为地转风;粗糙度取为0.1 m,模式层顶为5000 m,下边界设为固定边界条件,上边界设为自由边界条件;积分步长为10 min。模式积分一段时间达到稳定,为了与WBH01结果一致,以下结果都是140 h后的积分结果。
2.1 有效粗糙度法与直接参数化法的比较尽管有效粗糙度法对模式预报效果起到一定改进作用,相比于直接参数化法其缺点也不可忽略。
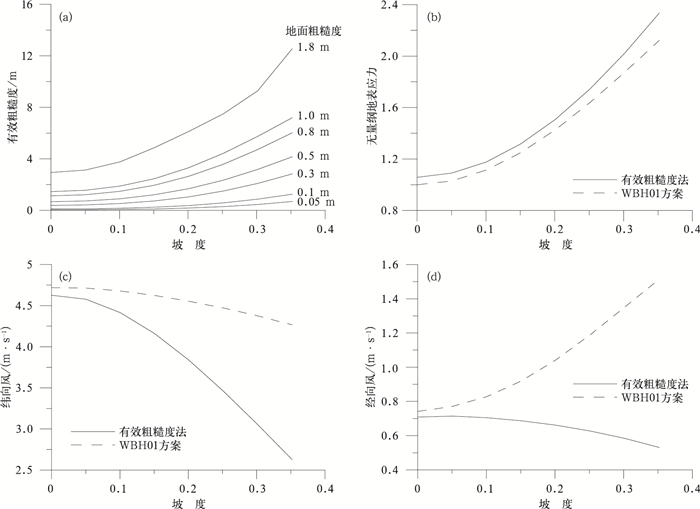
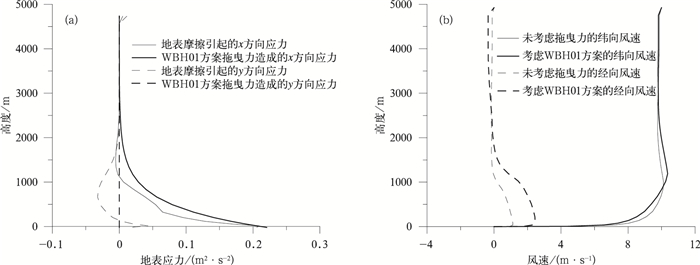
有效粗糙度法通过在地形起伏较大的地方增强粗糙度,使得一些地方有效粗糙度被过高估计 (如图 1a所示)。当坡度为0.3,地面粗糙度为1.8 m时,有效粗糙度可达10 m;有效粗糙度法只针对表面层,相比于直接参数化法可造成更大的地表应力 (如图 1b所示),有效粗糙度法造成的地表应力大于直接参数化法;有效粗糙度法对地面附近的风速造成虚假过低的现象 (如图 1c和1d所示)。有效粗糙度法对经向风速和纬向风速都有很大拖曳作用,而直接参数化方法针对的是边界层内一定厚度 (如图 2a的粗实线),地形造成的应力和地面磨擦造成的应力量级相当,且由低到高逐渐衰减。同时,直接参数化法模拟结果显示,地形湍流拖曳力对风的作用与理论分析一致,一方面,使得垂直于山脊的风被拖曳 (如图 2b所示) 在低层,未考虑拖曳力影响纬向风速大;另一方面,使得风向平行于山脊的方向偏转,考虑拖曳力影响经向风速大。
|
|
| 图 1. 有效粗糙度法和直接参数化法 (应用WBH01方案) 对低层气流的作用 (a) 有效粗糙度随坡度和地面粗糙度的变化,(b) 地表总应力 (被摩擦速度的平方标准化) 随坡度的变化,(c) 模式第1层 (5.5 m) 纬向风随坡度变化,(d) 模式第1层 (5.5 m) 经向风随坡度变化 Fig 1. The influence of effective roughness method and directed method (using WBH01 scheme) on the lower layer (a) the effective roughness changes with local roughness and slope, (b) the total surface stress (normalized by friction velocity square), (c) the zonal velocity changes of the 1st model level (5.5 m) with slope, (d) the meridional velocity changes of the 1st model level (5.5 m) with slope | |
|
|
| 图 2. 应力 (a) 和风速 (b) 垂直廓线 Fig 2. Momentum flux (a) and velocity (b) profile | |
此外,直接参数化法将地形湍流拖曳力当作单独一项来处理,使得方案的应用和改进极为方便,且物理意义更加清晰。模式可以单独输出该项进行研究,也可以与其他过程做对比,研究地形湍流拖曳力与其他的物理过程之间相互作用;还可以进一步对方案进行改进而不涉及其他过程,如将稳定度和上游风切变考虑到方案中,直接使拖曳力参数变成稳定度和上游风切变的适当函数即可;尤其是该方案关于层结作用的改进更为方便,因为当层结稳定时,山区上空未必仍然满足对数率,尤其是较高的地方,那么应用有效粗糙度法会有一些问题。如要考虑地形的各向异性,也可以将各向异性参数直接加入到该方案中来。
2.2 WBH01方案与BBW04方案的比较基于以上讨论,直接参数化法相比于有效粗糙度法具有诸多优点,为了证实应用于实际模式的BBW04方案的有效性和可行性,本研究从两个方面给出了WBH01方案和BBW04方案的模拟结果:① 针对水平尺度为5000 m、垂直山高为500 m的正弦起伏地形,输出应力垂直廓线,风速垂直廓线以及各项造成的动能倾向垂直廓线;② 改变理想地形的垂直尺度,考察地表拖曳力随坡度的变化。假定粗糙度z0=0.1 m,地转风为纬向风。尽管BBW04方案是针对实际的复杂地形而设计的,然而对于给定的理想地形,该方案与WBH01方案所表现的特性和作用应该相同。
在边界层内,越接近地面湍流活动越强。随着高度增加到边界层顶,湍流逐渐衰减到忽略不计;地面摩擦越大,湍流越强烈,由于地形起伏的存在,更能增强动量的垂直传输。一方面,湍流使得风速减弱,即拖曳作用;另一方面,在风速减弱的同时由于地转偏向力的作用使得低层风向低压偏转,即偏转作用,而增大的低层经向风速也相应地增强了低层经向动量的垂直交换。
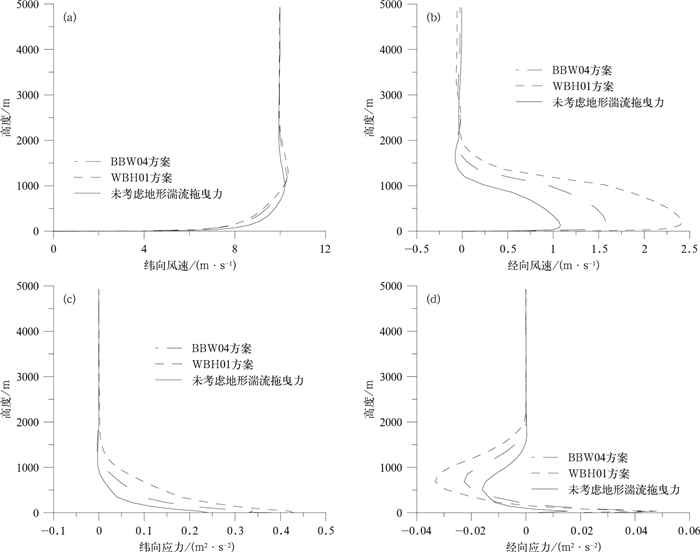
如图 3a,3b所示,在山高为500 m、起伏地形波长为5000 m的地形条件下,选用WBH01方案和BBW04方案都可以对低层纬向风造成拖曳,且拖曳作用极为接近;选用两个方案也都可以使低层经向风得以加强,即低层风偏向于山脊走向,值得注意的是,BBW04方案对低层风的偏转作用比WBH01方案的作用弱很多。这是因为BBW04方案忽略了山的各向异性,而未考虑风与山脊的夹角,那么,其偏转作用主要体现在地转偏向力的作用上。
|
|
| 图 3. 地形湍流拖曳力直接参数化法对纬向风速 (a)、经向风速 (b) 和纬向应力 (c)、经向应力 (d) 的影响 Fig 3. The influence of form drag on zonal velocity (a), meridional velocity (b) and zonal flux (c), meridional flux (d) | |
如图 3c,3d中应力垂直廓线所示,在没有考虑地形拖曳时,边界层内纬向动量的垂直通量随高度逐渐减小,且比考虑了地形湍流拖曳力之后要小;边界层内经向动量的垂直通量随高度先减小,达到最小值后再逐渐增加到0。这是由于地面摩擦和地形的拖曳作用,在假定地表风速为零、地转风为纬向风情形下,边界层内风速随高度逐渐增大,同时先向北偏转再逐渐转回到地转风。而地形的作用使得湍流得到加强,风的垂直梯度增大,近地层应力随之增大。比较WBH01方案和BBW04方案,两者在地表层造成的纬向应力相当,但由于前者的偏转作用强于后者,前者造成的低层经向应力也比后者大。
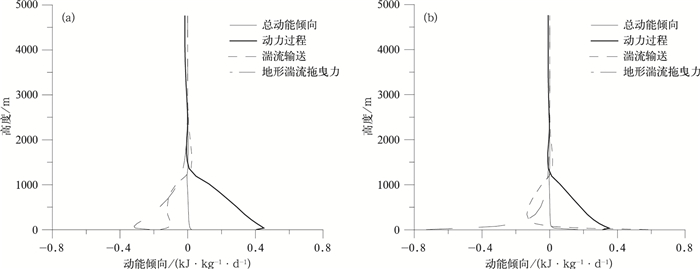
直接参数化法相比于有效粗糙度法的优势之一就是可以输出地形湍流拖曳力造成的动能倾向,从而与其他项造成的动能倾向比较以考察其相互作用。如图 4所示,总动能倾向为零,说明模式稳定;模式在固定气压强迫下运行,动力过程在各种情况下都不小于零;地形湍流拖曳力引起的动能倾向都不大于零,说明地形湍流拖曳力确实对气流有拖曳作用;地表摩擦引起的垂直扩散基本上处于负的一侧,但是低层也可能为正,这是由于低层地形拖曳力可导致风的局部逆转。相比于BBW04方案,WBH01方案造成的动能倾向在边界层较高的地方逐渐消失,即前者的垂直衰减尺度相对较大;而在近地层BBW04方案相比于WBH01方案造成的动量倾向的量级较大,选用前者时垂直扩散造成的动能倾向相对于考虑后者时小一些,即前者在低层对垂直扩散的补偿作用稍大。
|
|
| 图 4. WBH01方案 (a) 和BBW04方案 (b) 动能倾向诊断 Fig 4. The diagnosis of kinetic energy tendency for WBH01 scheme (a) and BBW04 scheme (b) | |
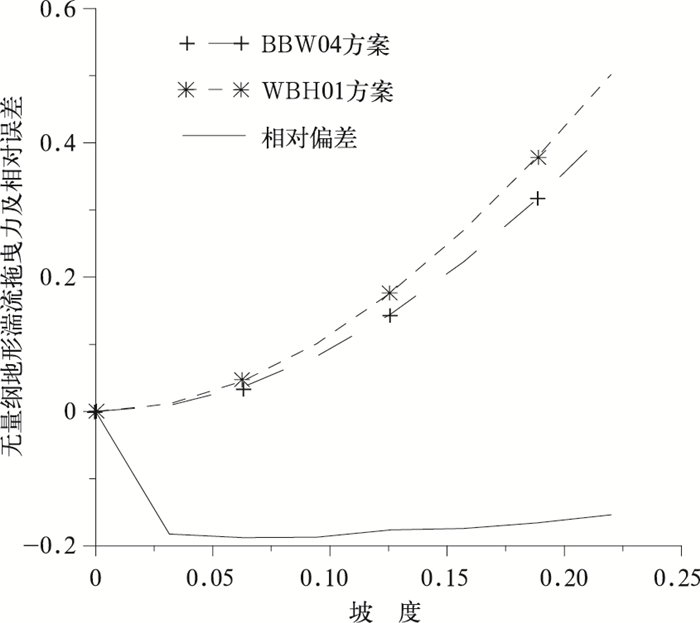
如前所述,地形湍流拖曳力随着地形坡度的增大而增大,成二次方关系,那么在数值天气预报模式中设计的参数化方案也必须满足这个基本关系。如图 5所示,地表地形湍流拖曳力 (用摩擦速度的平方进行了无量纲化) 随坡度的变化曲线,无量纲化了的地表地形湍流拖曳力随坡度的增大而增大,WBH01方案的地表拖曳力稍大于BBW04方案,考察其相对偏差也可以发现,后者的地形湍流拖曳力小于前者,但其差异只保持在20%以下。
|
|
| 图 5. 无量纲化地表地形湍流拖曳力随坡度变化 Fig 5. The change of the normalized surface form drag with slope | |
BBW04方案表面拖曳力的模拟合理,结合前述对风廓线、应力廓线和动能倾向廓线的讨论,认为BBW04方案在实用性的基础上,基本可以模拟出地形湍流拖曳力的性质和作用,那么要想验证其对模式预报效果的改进,须将此方案接入全模式中进行测试。
3 BBW04方案应用于GRAPES中尺度模式的个例模拟 3.1 GRAPES中尺度模式中的个例模拟简介GRAPES模式应用球坐标系下的全可压非静力平衡大气动力学和热力学方程组,采用半隐式-半拉格朗日时间积分方法,水平方向采用Arakawa-C网格分布,垂直方向采用Charney-Phillips跳层分布。GRAPES模式的垂直层次可选为均匀分层和非均匀分层,非均匀分层指的是在近地面边界层模式分层较密,而在模式大气的中高层分层较为稀疏。GRAPES模式上下边界条件分别是刚体边界条件和刚体自由面边界条件,区域模式侧边间条件为Davies松弛边界条件。模式包括了积云对流、微物理、辐射、行星边界层、陆面过程等物理过程,提供了多种可供选择的参数化方案[29-33]。
将BBW04方案接入GRAPES中尺度模式,分别选取冬季和夏季两个个例,来考察地形湍流拖曳力参数化方案对GRAPES模式预报效果的影响。两次个例模拟分别选取2008年12月8日和2009年8月2日做24 h预报模拟,起报时间为00:00(世界时,下同)。试验的具体情况如表 1所示,用GRAPES中尺度模式进行了嵌套。外围区域包括了中国疆域 (未包括部分南海区域) 及其周边地区,分辨率为15 km;内层嵌套区域主要包括青藏高原东部,西南横断山脉等地形起伏大的地区,以此来检验BBW04地形湍流拖曳力参数化方案在GRAPES中尺度模式中的作用,分辨率为6 km。外围试验积分时间步长为90 s,初始场和边界条件应用1°×1°的NCEP再分析资料;嵌套试验积分时间步长为30 s,初始场为其外围试验的26层等压面输出场。模式垂直层为31层,模式层顶高度为35 km,垂直分层为非均匀分层。
|
|
表 1 个例模拟简明表 Table 1 Cases concise table |
试验过程中所选的物理过程包括:WSM6云的微物理过程方案,RRTM长波辐射方案,简单短波辐射方案,MRF边界层方案,NOAH陆面过程方案,Betts-Miller积云对流参数化方案。
3.2 BBW04方案在GRAPES中尺度模式中的垂直特征地形湍流拖曳力作用于模式低层并向上逐渐衰减,为了考察BBW04方案在GRAPES中尺度模式中是否具有这样的特点,图 6给出了区域平均地形湍流拖曳力廓线随时间的变化,在I2B6试验中的模式面第1层区域平均拖曳力造成的速度倾向在低层可达10-3~10-4 m·s-2的量级,而在第3层就变得很小了 (模式面第3层和第5层对应高度分别为240 m和817 m)。速度倾向平均达到这个量级已经很可观了,而在某些局部地区其值会更高。从图 6也可以看出,尽管拖曳力在垂直方向上衰减很快,但是仍然有一定的垂直衰减尺度,这在物理上更合理,是优于有效粗糙度法的一个方面。图 6显示,地形湍流拖曳力造成的平均加速度在各个时次上有一些变化,由于地形参数没有改变,其量级变化应该主要由低层风切变引起。

|
|
| 图 6. 试验I2B6地形湍流拖曳力造成的区域平均速度倾向随时间的变化 (每个时次间隔3 h) Fig 6. The change of area average velocity tendency caused by form drag with time in case I2B6 (the time interval is 3 hours) | |
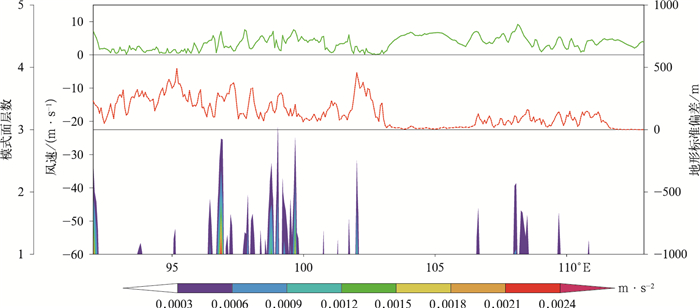
为了考察地形湍流拖曳力与实际地表起伏以及低层风速的关系,图 7给出了I2B6试验30°N地形湍流拖曳力全速度倾向图。由图 7可知,地形湍流拖曳力在模式面第3层以上衰减到很小;速度倾向,地形起伏和模式面第1层速度在空间上是波动的,地形起伏厉害的地方对应地形湍流拖曳加速度大的地方,同时又对应着模式面第1层全速度小的地方,以上三者的对应关系综合起来可以认为:地形起伏波峰对应地形湍流拖曳力波峰和模式面低层速度波谷。这样的分布具有其合理性,可以解释为地形起伏大,引起了大的地形湍流拖曳力,大的拖曳作用使得低层空气流速降低。应该说除此之外,低层流场的切变也会影响地形湍流拖曳力的分布,不过试验没有考察低层切变对地形湍流拖曳力的影响。
|
|
| 图 7. I2B6试验24 h预报场地形湍流拖曳力造成的速度倾向沿30°N垂直剖面图 (阴影),模式面第1层全风速大小 (绿线) 和地形标准偏差 (红线) Fig 7. 30°N zonal section of velocity tendency (shaded area) caused by 24-hour prediction form drag, the 1st level wind speed (green line) and orographic standard deviation (red line) in case I2B6 | |
综上所述,地形湍流拖曳力在模式中的表现与理论描述一致,主要在大气低层起作用,量级可达10-4~10-3 m·s-2,具有一定的垂直衰减厚度;地形起伏和低层风切变影响地形湍流拖曳力,地形湍流拖曳力对低层流场产生拖曳反过来影响低层流场。
3.3 结果分析无论一个次网格尺度物理过程的作用有多么重要,最终能够说明问题的是其能够改进数值模式的预报效果。在考察了地形湍流拖曳力的重要性、理论依据、参数化方案及其在模式中的性质之后,需要进一步讨论次网格尺度地形湍流拖曳力参数化方案对模式的作用。
为了考察地形湍流拖曳力参数化方案在模式中对地形起伏地区低层流场的作用,利用GRAPES中尺度模式嵌套6 km分辨率对青藏高原东部和我国西南山区进行了数值模拟。图 8给出了6 km分辨率个例模拟结果与NCEP再分析资料的10 m风相对偏差分布图,可以看出,试验I8B6中10 m风相对偏差大值区的值明显比I8N6中的小,而试验I2B6中除了个别点外,10 m风相对偏差大值区的值普遍比试验I2N6中的小。

|
|
| 图 8. 风速相对偏差分布 (单位:m·s-1) Fig 8. The relative bias of wind speed (unit:m·s-1) | |
GRAPES中尺度模式在地形起伏区域10 m风偏差较大,模式考虑地形湍流拖曳力参数化方案后,可以对10 m风的预报效果达到一定程度上的改进,尤以地形起伏区域为主。尽管考虑了BBW04地形湍流拖曳力方案可以在一定程度上改进了10 m风的预报,但是仍然存在较大偏差,其原因需要进一步研究。
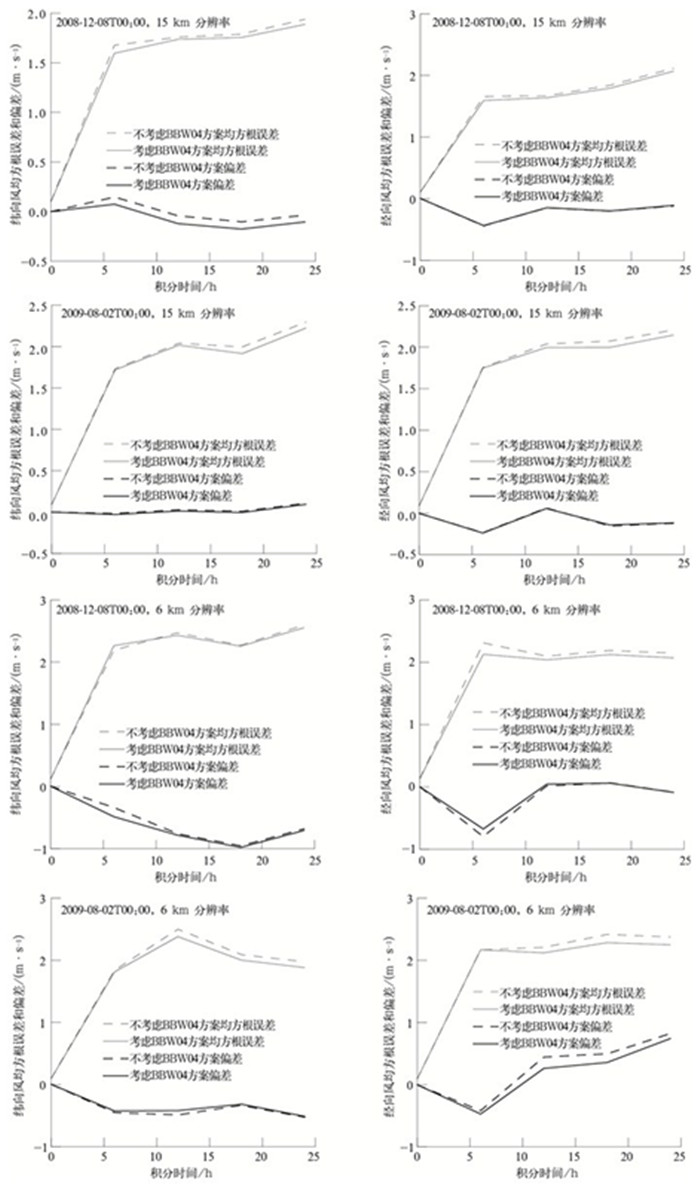
上文已经直观地考察了地形湍流拖曳力对10 m高度风和表面气压的影响,为了讨论其对模式近地层预报量的总体影响,图 9给出了一系列模拟结果与NCEP再分析资料的10 m高度风速均方根误差和区域平均偏差随积分时间的变化图。
|
|
| 图 9. 10 m高度纬向风和经向风速考虑与不考虑BBW04方案的均方根误差和偏差 Fig 9. RMS error and bias of 10-meter zonal and meridional winds between cases with and without BBW04 scheme | |
由图 9可知,从15 km到2 km分辨率的所有个例试验,考虑了地形湍流拖曳力之后,均方根误差相比于没有考虑地形湍流拖曳力变小,模式对10 m高度风的预报效果有不同程度的提高。分辨率为15 km时模式对低层风的预报效果有一定改进,冬季个例从6 h预报到24 h预报,均方根误差和平均偏差的变化相对平稳;而夏季个例均方根误差发展有些波动,12 h之后,预报效果提高更为显著。分辨率为6 km时,对冬季个例的10 m高度纬向风预报效果影响不大,而10 m高度经向风的预报效果有较大提高;夏季个例预报效果提高显著,考虑地形湍流拖曳力方案后均方根误差减小,偏差更接近零线。
除了讨论10 m高度风的预报效果,还考察了2 m高度温度和表面气压的平均偏差和均方根误差随积分时间的变化,结果显示:考虑地形湍流拖曳力对2 m高度温度和表面气压的预报效果无显著影响。从理论上分析,流场气压场和温度场应该相互联系,预报效果应该得到一致提高;然而,地形湍流拖曳力以动力拖曳为主,且其作用只占所有次网格尺度地形作用中的一部分,因此要进一步提高模式低层预报量的预报效果,还需要考察其他原因,包括其他次网格尺度地形作用。
综上所述,考虑次网格尺度地形湍流拖曳力参数化方案对模式10 m高度风的预报效果有一定程度的提高,BBW04方案在较长预报时间内对低层风场预报效果有较高改善。然而地形湍流拖曳力并未使得模式对近地层其他气象要素预报效果有显著提高。且各个近地层气象要素的预报场与NCEP再分析资料之间仍然存在较大的偏差,其原因值得深入探究。
4 结论和讨论本文在广泛调研国际上关于次网格尺度地形拖曳力方面研究的基础上,首先,讨论了模式考虑次网格尺度地形拖曳力参数化方案的必要性,以及当今国际上较为流行的各类地形湍流拖曳力参数化方案;之后,应用单柱模式,模拟并讨论了直接参数化法与有效粗糙度法的优劣,比较了WBH01方案和BBW04方案的各自特点;最后,将BBW04方案接入GRAPES中尺度模式3.0版本,分别对冬、夏两个个例进行了模拟,验证了次网格尺度地形湍流拖曳力在模式中的垂直结构,检验了地形湍流拖曳力参数化对模式低层风场的改进,得出一些初步结论:
1) 针对我国复杂地形,估算了次网格尺度地形湍流拖曳力,表明次网格尺度地形作用不可忽略,其中地形湍流拖曳力对10 m高度风的拖曳加速度局地最大可达100 m·s-2的量级,对模式面低层的拖曳加速度平均可达10-4 ~10-3m·s-2的量级。
2) 比较了传统的有效粗糙度法与具有深厚理论基础的地形湍流拖曳力直接参数化方案,结果表明:直接参数化法比有效粗糙度法在理论和实际应用方面更为合理。有效粗糙度法过高估计局部地形起伏区域的粗糙度可造成低层虚假风速,且只强调地表拖曳作用,对风没有偏转作用,尽管已被广泛使用,且在模式中证明具有积极的效果,但直接参数化方法更具有深厚的理论基础,可以对垂直山脊的风起拖曳作用,并使风偏向于平行于山脊的方向,且具有一定的垂直衰减厚度,作为一个独立的物理过程,更容易考察其与其他过程的相互作用,在实际应用中更有潜力。
3) 考察了地形湍流拖曳力和垂直扩散过程的相对贡献,表明了地形湍流拖曳力和垂直扩散有相互补偿的作用。
4) 通过单柱模式考察了WBH01方案和BBW04方案的各自特点,表明BBW04方案针对5 km左右的各向同性地形,除了对风的偏转作用与前者差异较大之外,其他特性与前者相似,可以模拟出地形湍流拖曳力的性质。
5) 通过GRAPES中尺度模式的实况模拟,得出了地形湍流拖曳力随高度逐渐减小,地形起伏区域强对应拖曳力大和风速小的区域;证实了考虑地形湍流拖曳力可以改进模式低层风场的预报效果。
同时,也发现一些有待进一步探讨的问题:
1) 当今模式中应用的地形湍流拖曳力参数化方案都是假定次网格尺度地形各向同性,应用单一的地形参数,需要应用更为全面和真实的地形参数。
2) 将BBW04方案接入GRAPES模式之后需要进一步检验,以考察地形湍流拖曳力对模式预报效果的影响,并调整参数,以便得到对GRAPES模式来说更适用的参数化方案。
3) 诊断造成模式对近地层气象要素预报量偏差的原因,并探索相应改进方法。
| [1] | 叶笃正, 顾震潮. 西藏高原对于东亚大气环流及中国天气的影响. 科学通报, 1955, 6: 28–33. |
| [2] | 叶笃正. 西藏高原对于大气环流影响的季节变化. 气象学报, 1952, 23, (1): 33–47. |
| [3] | 叶笃正. 小地形对于气流的影响. 气象学报, 1956, 27, (3): 243–265. DOI:10.11676/qxxb1956.018 |
| [4] | 钱永甫, 颜宏, 王谦谦, 等. 行星大气中地形效应的数值模拟. 北京: 科学出版社, 1988: 217. |
| [5] | 卢敬华, 陈刚毅. 中小地形对局地天气气候的影响. 成都气象学院学报, 1989, 8: 1–9. |
| [6] | Davies L A, Brown A R. Assessment of which scales of orography can be credibly resolved in a numerical model. Q J R Meteorol Soc, 2001, 42: 828–841. |
| [7] | Jackson P S, Hunt C R. Turbulent wind flow over a low hill. Quart J Roy Met Soc, 1975, 101: 929–955. DOI:10.1002/(ISSN)1477-870X |
| [8] | Sykes R I. An asymptotic theory of incompressible turbulent flow over a small hump. J Fuid Mech, 1980, 101: 647–670. DOI:10.1017/S002211208000184X |
| [9] | Hunt J C R, Leibovich S, Richards K J. Turbulent shear flows over low hills. Q J R Meteorol Soc, 1988, 114: 1435–1471. DOI:10.1002/(ISSN)1477-870X |
| [10] | Belcher S E, Newley T, Hunt J. The drag on an undulating surface induced by the flow of a turbulent boundary layer. J Fluid Mech, 1993, 249: 557–596. DOI:10.1017/S0022112093001296 |
| [11] | Wood N, Mason P. The pressure force induced by neutral, turbulent flow over hills. Quart J Roy Met Soc, 1993, 119: 1233–1267. DOI:10.1002/(ISSN)1477-870X |
| [12] | Belcher S, Wood N. Form and wave drag due to stably stratified turbulent flow over low ridges. Quart J Roy Met Soc, 1996, 122: 863–902. DOI:10.1002/(ISSN)1477-870X |
| [13] | Wood N, Brown A R, Hewer F E. Parametrizing the effects of orography on the boundary layer: An alternative to effective roughness lengths. Quart J Roy Met Soc, 2001, 127: 759–777. |
| [14] | Brown A R, Wood N. Turbulent form drag on anisotropic three-dimensional orography. Bound-Layer Meteor, 2001, 101: 229–241. DOI:10.1023/A:1019251128414 |
| [15] | Brown A R, Wood N. Properties and parameterization of the stable boundary layer over moderate topography. Journal of the Atmospheric Sciences, 2003, 60: 2797–2808. DOI:10.1175/1520-0469(2003)060<2797:PAPOTS>2.0.CO;2 |
| [16] | Allen T, Brown A R. Modeling of turbulent form drag in convective conditions. Bound-Layer Meteor, 2006, 118: 421–429. DOI:10.1007/s10546-005-9002-z |
| [17] | Mason P. On the Parameterization of the Orographic Drag. Technical Report, Proc. Seminar on Physical Parametrization for Numerical Models of the Atmosphere, ECMWF. 1985: 139-165. |
| [18] | Taylor P, Sykes R, Mason P. On the parametrization of drag over small-scale topography in neutrally stratifled boundary-layer flow. Bound-Layer Meteor, 1989, 49: 409–422. |
| [19] | Grant A L M, Mason P. Observations of boundary-layer structure over complex terrain. Quart J Roy Met Soc, 1990, 116: 159–186. DOI:10.1002/(ISSN)1477-870X |
| [20] | Newley T J. Turbulent Airflow over Hills. Cambridge: University of Cambridge, 1985. |
| [21] | Nappo C J. Mesoscale flow over complex terrain during the Eastern Tennessee Trajectory Experiment (ETTEX). J Appl Meteorol, 1977, 16: 1186–1196. DOI:10.1175/1520-0450(1977)016<1186:MFOCTD>2.0.CO;2 |
| [22] | Thompson R S. Note on the aerodynamic roughness-length for complex terrain. J Appl Meteorol, 1978, 17: 1402–1403. DOI:10.1175/1520-0450(1978)017<1402:NOTARL>2.0.CO;2 |
| [23] | Kustas W P, Brutsaert W. Wind profile constants in a neutral atmospheric boundary layer over complex terrain. Bound-Layer Meteor, 1986, 34: 35–54. DOI:10.1007/BF00120907 |
| [24] | Hopwood W P. Radiosonde observation of boundary layer characteristics over two types of complex terrain. Annales Geophysicae, 1991, 9: 224–225. |
| [25] | Rontu L. A study on parametrization of orography-related momentum fluxes in a synoptic-scale NWP model. Tellus, 2006, 58: 68–81. |
| [26] | Beljaars A C M, Brown A R, Wood N. A new parameterization of turbulent orographic form drag. Q J R Meteoro Soc, 2004, 130: 1327–1347. DOI:10.1256/qj.03.73 |
| [27] | Hobson J M, Wood N, Brown A R. Large-eddy simulations of neutrally steratified flow over surfaces with spatially varying roughness length. Q J R Neteorol Soc, 1999, 124: 1937–1958. |
| [28] | Yamada T, Mellor G. A simulation of the Wangara atmospheric boundary layer data. Journal of the Atmospheric Sciences, 1975, 32: 2309–2329. DOI:10.1175/1520-0469(1975)032<2309:ASOTWA>2.0.CO;2 |
| [29] | 胡江林, 沈学顺, 张红亮, 等. GRAPES模式动力框架的长期积分特征. 应用气象学报, 2007, 18, (3): 276–284. |
| [30] | 陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2007, 17, (6): 773–777. |
| [31] | 伍湘君, 金之雁, 黄丽萍, 等. GRAPES模式软件框架与实现. 应用气象学报, 2005, 16, (4): 539–546. DOI:10.11898/1001-7313.20050415 |
| [32] | 孙晶, 楼小凤, 胡志晋, 等. CAMS复杂云微物理方案与GRAPES模式耦合的数值试验. 应用气象学报, 2008, 19, (3): 315–325. DOI:10.11898/1001-7313.20080307 |
| [33] | 陈峰峰, 王光辉, 沈学顺, 等. Cascade插值方法在GRAPES模式中的应用. 应用气象学报, 2009, 20, (2): 164–170. DOI:10.11898/1001-7313.20090205 |
 2011, 22 (2): 169-181
2011, 22 (2): 169-181



