2. 国家气候中心,北京 100081
2. National Climate Center, Beijing 100081
极端天气气候事件对社会经济和人民生命财产具有巨大的破坏力,IPCC第4次评估报告列出了由极端天气和气候事件变化可能引起的气候变化影响的示例,其中极端高温事件列居首位。在全球变暖的大背景下,极端高温事件频繁影响北半球,且影响范围越来越广。2003年欧洲出现百年罕见的高温热浪,导致1.9万人死亡,与此同时,多个国家出现罕见干旱,并引发火灾;2009年夏季,我国很多地区日最高气温突破历史极值,部分地区持续拉响高温橙色警报。研究亦已表明,20世纪80年代开始我国气温升高,90年代进入加速增暖的阶段,极端高温事件的强度和频次变化显著,北方地区增温尤为明显,极端高温日数明显增多,而我国东部地区的高温日数有减小趋势,未来我国大部分地区的极端高温频次将呈增加趋势[1-8]。
目前,数理统计方法已经被广泛应用于研究极端天气气候事件[9-15],如通过极值分布理论来研究极端温度事件的统计特征[16-23],已有的研究方法大多基于所分析要素符合正态分布这一基本假设,事实并非如此,对于同一种气象要素而言,不同地区的概率分布型亦有可能不相同。欧进萍等[24]在研究哈尔滨气温的变化时指出,正态分布可以很好地描述各月极端气温,但对温度日较差因其存在一定偏度,拟合效果不佳,若仍然直接采用基于正态分布的数理方法来研究哈尔滨地区的日较差,得到的结论可能有一定偏差。
鉴于各种气象要素的概率分布存在不同程度的偏态特征,本文引进了一种偏态数据分析方法——Box-Cox变换,其作用在于将具有一定偏态分布的时间序列转换为近似符合正态分布的新序列,以便利用已有的数理统计方法研究数据的统计规律和特征,该方法在金融、生物医学等领域中有广泛应用[25-28]。本文基于偏态函数的偏态指数和最概然高温极值,探讨了我国夏季高温极值的概率分布特征及其在变暖前后的变化,并研究了二者对我国气温变化的响应。
1 资料和方法 1.1 资料资料取自国家气象信息中心气象资料室提供的中国国际交换站中无过多缺测记录的167个台站的日最高气温,资料长度为1961—2008年。
1.2 百分位阈值法在本文中取夏季同日资料样本第90百分位数作为高温极值阈值。Bonsal等[29]指出,如果某时间序列长度为n,将这n个值按升序排列x1,x2,…,xm,…,xn,某个值小于或等于xm的概率为
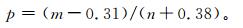
|
(1) |
式 (1) 中,m为xm的序号,即如果有100个值,那么样本第90百分位数为排序后的x90(p=89.35%) 和x91(p=90.35%) 的线性插值。式 (1) 常用于确定各种极端事件的百分位阈值,计算比较方便。按照式 (1) 的估计方法,将各站点资料中的夏季同日资料的日最高气温按升序排列,得到该日最高气温的第90百分位数,所有超过该百分位数的温度值即为该日的高温极值。
1.3 偏态分布函数在研究我国夏季高温极值分布时,通常会出现不同程度的正偏与负偏现象,若一律采用高斯分布函数拟合,势必会在统计问题中带来较大的偏差。Box-Cox变换为解决这一问题提供了新的途径,通过该变换后的数据满足正态性假定条件,可以据此求得夏季高温极值的偏态分布函数。
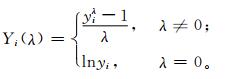
|
(2) |
式 (2) 中,λ是一个待定的变换参数,可利用极大似然法估计获得。
由变换后数据满足的正态性假定条件,可以推导出原高温极值序列的偏态分布函数形式:

|
(3) |
式 (3) 中,λ为高温极值序列经Box-Cox变换所得到的衡量偏态程度的指数,本文定义其为偏态指数;σ1为Box-Cox变换后新序列的标准差。λ<1,表明原始高温极值序列的分布呈正偏,即分布的右尾比左尾长;λ>1,表明原始高温极值数据序列分布呈负偏,即分布的左尾长于右尾。当λ=1时,式 (3) 可以写为

|
(4) |
显然,当λ=1时,式 (4) 是式 (3) 的特例,即呈现高斯分布。
图 1a、图 1b、图 1c分别为3种典型的夏季高温极值分布型:正偏、负偏、高斯分布,对应的偏态指数λ分别为-12.28,7.55,1.01。根据概率密度分布函数的物理意义,本文将偏态分布函数拟合曲线中概率密度最大值对应的高温极值定义为最概然高温极值,意味着在某站点最有可能出现的高温极值,简记为Tmaxp。从图 1不难发现,λ<1时,处于正偏,Tmaxp<T(T为夏季高温极值的均值),低于高温极值均值的极端温度偏多;λ>1时,处于负偏,Tmaxp>T,高于高温极值均值的温度偏多;λ接近1时,Tmaxp≈T,偏态函数与高斯函数拟合线几乎重合,这也从侧面验证了偏态函数的适用性。Tmaxp与T的偏离程度,既取决于偏态指数λ值偏离1的大小,也取决于分布峰的凸平度,即峰度系数的大小。

|
|
| 图 1. 我国夏季高温极值的正偏、负偏、高斯分布 (直方图对应夏季高温极值的概率统计分布,圈点线为高斯拟合,实点线为偏态函数拟合)(a) 海南东方站,(b) 浙江杭州站,(c) 内蒙古化德站 Fig 1. The positive skew, negative skew, and normal distribution of summer extreme high temperatures in China (the histogram is experience distribution, with Gaussian fitting in hollow points line, skewness fitting in solid points line) (a) Dongfang station in Hainan, (b) Hangzhou station in Zhejiang, (c) Huade station in Inner Mongolia | |
2 我国夏季高温极值的概率分布特征
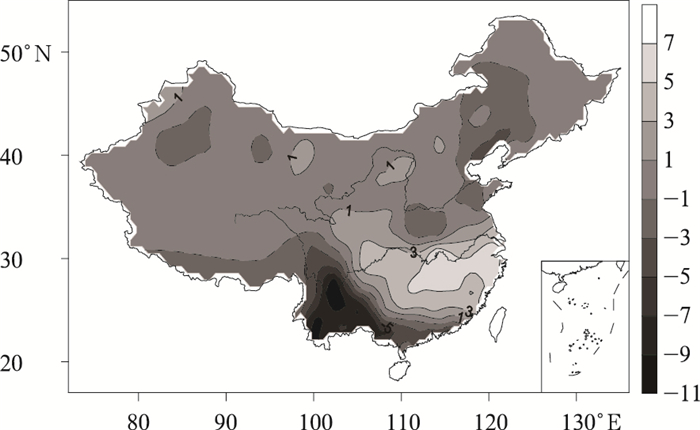
图 2展示了我国夏季高温极值的偏态指数的空间分布情况。除四川盆地和长江中下游及其以南地区外,我国其余大部分地区偏态指数λ<1,意味着在这些地区夏季高温极值的概率密度分布呈现正偏。西南地区东南部、华南大部、华北地区东部及辽宁北部、内蒙古中东部、河南北部、山东中西部、西藏南部等地偏态指数普遍在-3~-1之间,其中云南、广西西部、川西高原等地的偏态指数在-7~-3之间,云南大部地区小于-7,局部地区小于-9,这表明:我国西南地区东南部夏季高温极值正偏现象最为显著,其次是华北地区东部及内蒙古中东部等地。对于呈正偏分布地区,最概然温度低于高温极值的平均值,夏季异常高温出现的几率较小。长江中下游及其以南地区、四川盆地大部等地的偏态指数普遍大于1,表明上述地区的夏季高温极值分布主要呈现负偏态势,其中长江中下游及其以南地区的负偏更为明显,这意味着在这些地区最概然高温极值大于高温极值的平均值,即Tmaxp>T,在夏季更易出现高温极值。
|
|
| 图 2. 1961—2008年我国夏季高温极值的偏态指数分布图 Fig 2. The skewness index of summer extreme high temperatures in China during 1961—2008 | |
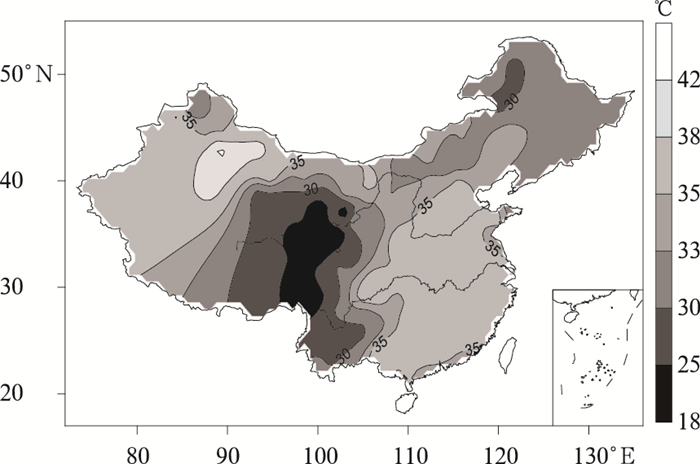
我国夏季最概然高温极值Tmaxp的范围为18~42℃(图 3),根据其值大小可以大致分为4个区域:我国中东部和西北西部地区为两个高值区,新疆吐鲁番的最概然高温极值最高,表明吐鲁番是我国高温极值强度最强的一个区域;东北地区及内蒙古大部为次高值区;西北地区中部和西南地区西部及云南等地为低值区,这一区域最概然高温极值普遍在30℃以下,其中青海东部局部地区的最概然高温极值在22℃以下,是我国夏季最概然高温极值最低的地区。结合图 2可知,该地区高温极值分布呈现正偏,最概然高温极值低于平均高温极值,可知其为我国极端高温事件最不易发生的区域。
|
|
| 图 3. 1961—2008年我国夏季最概然高温极值的分布图 Fig 3. The most probable extreme high temperature in China during 1961—2008 | |
3 我国夏季高温极值的演变特征
偏态指数λ可以定量地表征高温极值的分布型特征,即其相对于高斯拟合分布型的偏离程度,基于此,本文提出了有别于高温极值平均值的最概然高温极值Tmaxp,将最概然高温极值作为极端高温事件的背景场,来分析我国夏季高温极值的演变特征。很多研究已表明:我国自20世纪80年代开始变暖,为此将48年的资料分为1961—1980年和1981—2008年两个时段,来分析在变暖前和变暖后我国夏季高温极值的分布型以及高温极值的演变特征,并研究了二者之间的联系。
3.1 我国夏季高温极值偏态指数的变化特征将1981—2008年和1961—1980年两个时段的夏季高温极值偏态指数相减,可得到变暖前后我国夏季高温极值偏态指数变化的空间分布图 (图 4)。从图 4中不难发现,我国大部分地区的偏态指数呈减小态势,其中新疆大部、内蒙古、甘肃至四川等地偏态指数λ的减小,意味着其分布型由负偏向正偏过度,即最概然高温极值由大于高温极值均值向小于高温极值均值转变;而长江中下游以南地区,偏态指数λ减小主要体现为分布型负偏的减弱,且减弱趋势明显,这同时也表明最概然高温极值向高温极值平均值逼近。偏态指数λ增大的地区主要集中在河南大部、山东中西部、云南大部以及西藏东部,其分布型的变化主要体现为正偏减弱,亦表明这些地区的最概然高温极值趋向高温极值均值。
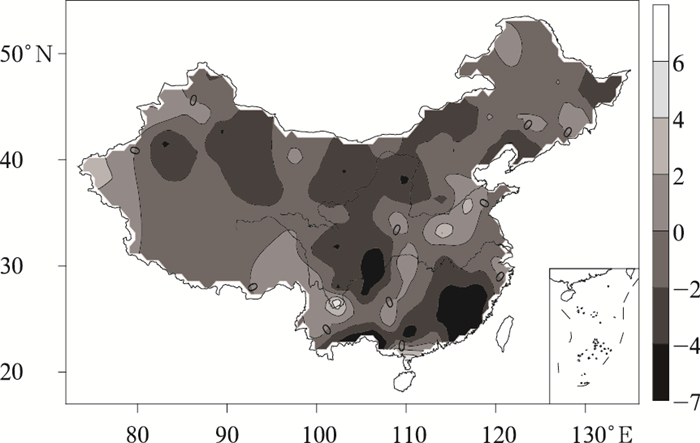
|
|
| 图 4. 20世纪80年代前后我国夏季高温极值偏态指数变化分布 Fig 4. The changes of the skewness index of extreme high temperatures in China before and after 1980s | |
3.2 我国夏季最概然高温极值的演变特征
类似于变暖前后偏态指数的分析,图 5给出了20世纪80年代变暖前后,我国夏季最概然高温极值变化图。华北中北部、东北大部及内蒙古大部、西北地区中部和东部、西南大部、华南大部等地区,即最概然高温极值Tmaxp相对次高值和低值区,最概然高温极值有增大趋势,且增温幅度较大,其增温最强的地区位于西藏中东部和内蒙古东北部,局地可达1.8℃左右;而在我国中东部和新疆大部,即最概然高温极值Tmaxp的高值区,最概然高温极值却呈减小趋势,江淮、江汉、黄淮西部以及新疆的西北部降温幅度最大,同样可达1.8℃左右。
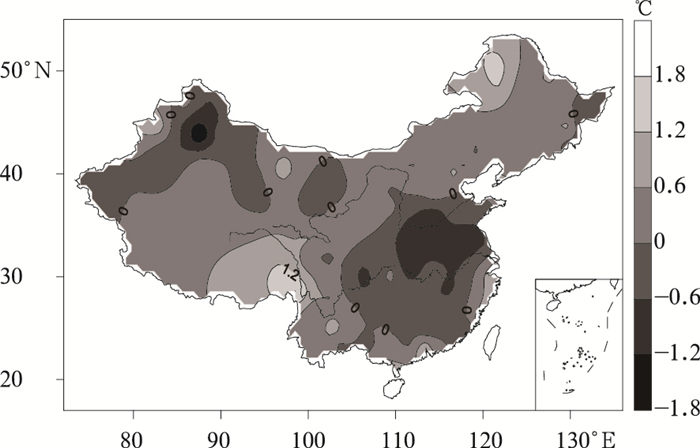
|
|
| 图 5. 20世纪80年代前后我国夏季最概然高温极值变化分布 Fig 5. The changes of the most probable extreme high temperature in China before and after 1980s | |
3.3 剔除不同尺度高温极值对偏态指数和最概然高温极值的影响
偏态指数λ的变化仅仅体现了概率分布形状的变化,其实质是数据分布结构的改变。在气温记录中,由于气候变化在不同时期内可能具有不同特征,或是在不同时间尺度下可能具有不同的规律,当剔除某个时间尺度内的高温极值,无论是该尺度内高温极值的个数,高温极值的强度,还是高温极值的聚散程度,都可能会导致其分布型或最概然高温极值Tmaxp发生改变。鉴于此,本文分别考虑了滑动剔除2年、5年、10年等3种不同时间尺度的高温极值对原始极值分布的偏态指数和最概然高温极值的影响。以滑动剔除2年尺度的极值为例,每次仅剔除2年尺度的极值,然后分别计算剔除极值后与未剔除前偏态指数之差,再以2年为步长滑动剔除2年极值,重复上述操作直至序列末尾。
图 6为剔除不同尺度极值后偏态指数λ变化的均值分布,图 6a, 图 6b,图 6c分别为剔除2年、5年、10年的情况。从图 6可知,剔除2年、5年、10年后,偏态指数λ的变化虽然在数值上有所差异,即被剔除极值的时间尺度越大,对偏态指数λ的影响越大,但偏态指数变化的空间分布却比较类似,无论是剔除2年、5年,还是10年的极值,除长江中下游以南大部地区的偏态指数λ影响相对较大外,我国其余大部地区受到的影响相对较小。

|
|
| 图 6. 剔除不同尺度极值后偏态指数变化的均值分布图 (a) 剔除2年尺度,(b) 剔除5年尺度,(c) 剔除10年尺度 Fig 6. The changes in skewness index after removing different scales extreme high temperatures (a) removing 2-year imescale, (b) removing 5-year timescale, (c) removing 10-year timescale | |
图 7展示了滑动剔除不同尺度极值后最概然高温极值Tmaxp变化的均值分布图,图 7a、图 7b、图 7c分别为剔除2年、5年、10年尺度的情况。无论是剔除2年、5年还是10年尺度的极值后,最概然高温极值Tmaxp所受到的影响都很小,且最概然高温极值Tmaxp平均变幅的空间分布基本一致,全国大部地区的最概然高温极值Tmaxp平均变幅在0.2℃以内。可见,滑动剔除10年尺度内的极值数据,最概然高温极值Tmaxp的变化相对比较稳定。这表明:最概然高温极值Tmaxp是衡量极端高温事件的较稳定量之一。
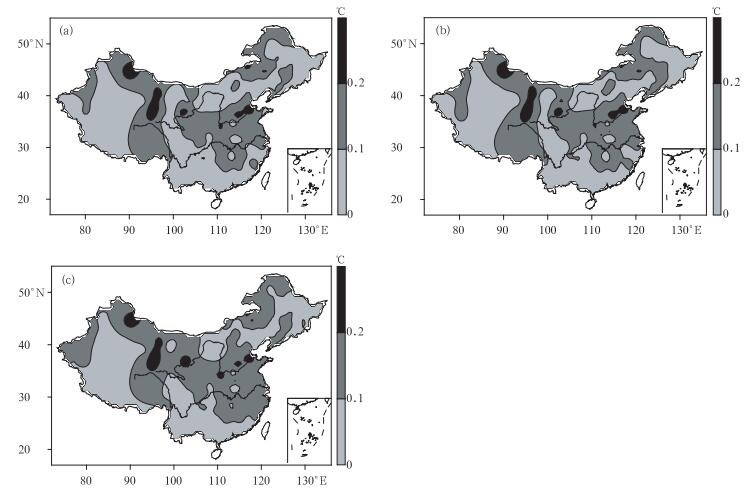
|
|
| 图 7. 剔除不同尺度极值后最概然高温极值变化的均值分布图 (a) 剔除2年尺度,(b) 剔除5年尺度,(c) 剔除10年尺度 Fig 7. The changes in the most probable extreme high temperature after removing different scales extreme high temperatures (a) removing 2-year timescale, (b) removing 5-year timescale, (c) removing 10-year timescale | |
4 结论
通过本文的研究,得到以下主要结论:
1) 利用偏态指数和最概然高温极值研究我国夏季高温极值的概率分布特征,结果表明:我国大部分台站夏季高温极值的概率分布为正偏分布型,西南地区东南部正偏尤为明显,而长江中下游以南地区负偏比较明显。夏季最概然高温极值的高值区位于我国东部和西北地区西部,东北地区及内蒙古大部为次高值区,西北地区中部和西南地区大部等地为低值区。
2) 20世纪80年代前后,我国中东部大部、西南地区中部及新疆大部、内蒙古东北部等地,偏态指数变化比较显著,正偏现象和负偏现象均呈现减弱的趋势,最概然高温极值明显向高温极值均值逼近。在最概然高温极值的高值区,呈降温趋势;最概然高温极值的相对次高值和低值区,有增温趋势。
3) 滑动剔除不同时间尺度的极值,偏态指数仅在长江中下游以南地区变化稍大些,而对我国其余大部地区高温极值分布型的影响很小;随时间尺度的增大,偏态指数所受影响越大。此外,数据的剔除对最概然高温极值几乎没有影响,可见它是个比较稳定的量,将其作为定义极端高温事件阈值的一种可能的新途径。
| [1] | 胡宜昌, 董文杰, 何勇. 21世纪初极端天气气候事件研究进展. 地球科学进展, 2007, 22, (10): 1066–1075. DOI:10.3321/j.issn:1001-8166.2007.10.011 |
| [2] | 魏凤英, 曹鸿兴, 王丽萍. 20世纪80—90年代中国气候增暖进程的统计事实. 应用气象学报, 2003, 14, (1): 79–86. |
| [3] | 王馥棠. 近十年来我国气候变暖影响研究的若干进展. 应用气象学报, 2002, 13, (6): 755–766. |
| [4] | 陈隆勋, 朱文琴, 王文, 等. 中国近45年来气候变化的研究. 气象学报, 1998, 56, (3): 257–271. DOI:10.11676/qxxb1998.023 |
| [5] | 丁一汇, 任国玉, 石广玉, 等. 气候变化国家评估报告 (Ⅰ):中国气候变化的历史和未来趋势. 气候变化研究进展, 2006, 2, (1): 4–8. |
| [6] | 张勇, 曹丽娟, 许吟隆, 等. 未来我国极端温度事件变化情景分析. 应用气象学报, 2008, 19, (6): 655–660. |
| [7] | 杨萍, 刘伟东, 王启光, 等. 近40年我国极端温度变化趋势和季节特征. 应用气象学报, 2010, 21, (1): 29–36. |
| [8] | 杨萍, 封国林, 刘伟东, 等. 空间点过程理论在极端气候事件中的应用研究. 应用气象学报, 2010, 21, (3): 352–359. |
| [9] | Render S, Petersen M R. Role of global warming on the statistics of record-breaking temperatures. Phys Rev E, 2006, 74: 0611141–06111414. |
| [10] | Györgyi G, Moloney N R, Rácz Z. Extreme statistics for time series: Distribution of the high relative to the initial value. Phys Rev E, 2007, 76: 0411191–04111912. |
| [11] | 封国林, 王启光, 侯威, 等. 气象领域极端事件的长程相关性. 物理学报, 2009, 58, (4): 2853–2861. DOI:10.7498/aps.58.2853 |
| [12] | 章大全, 钱忠华. 利用中值检测方法研究近50年中国极端气温变化趋势. 物理学报, 2008, 57, (7): 4634–4640. DOI:10.7498/aps.57.4634 |
| [13] | 侯威, 杨萍, 封国林. 中国极端干旱事件的年代际变化及其成因. 物理学报, 2008, 57, (6): 3932–3940. DOI:10.7498/aps.57.3932 |
| [14] | 龚志强, 王晓娟, 支蓉, 等. 中国近58年温度极端事件的区域特征及其与气候突变的联系. 物理学报, 2008, 58, (6): 4342–4353. |
| [15] | 熊安元. 长江中游持续暴雨期中尺度降水系统的统计分析. 应用气象学报, 1995, 6, (4): 496–500. |
| [16] | Sabhapandit S, Majumdar S N. Density of near-extreme events. Phys Rev Lett, 2007, 98: 142011–142014. |
| [17] | Györgyi G, Moloney N R, Ozogány K, et al. Finite-size scaling in extreme statistics. Phys Rev Lett, 2008, 100: 2106011–2106014. |
| [18] | Labraga J C, Villalba R. Climate in the Monte Desert: Past trends, present conditions, and future projections. Journal of Arid Environments, 2009, 73: 154–163. DOI:10.1016/j.jaridenv.2008.03.016 |
| [19] | Clarke R T, Paiva R D de, Uvo C B. Comparison of methods for analysis of extremes when records are fragmented: A case study using Amazon basin rainfall data. J Hydrol, 2009, 368: 26–29. DOI:10.1016/j.jhydrol.2009.01.025 |
| [20] | Xu Y, Xu C H, Gao X J, et al. Projected changes in temperature and precipitation extremes over the Yangtze River Basin of China in the 21st century. Quaternary International, 2009, 208: 44–52. DOI:10.1016/j.quaint.2008.12.020 |
| [21] | 丁裕国, 刘吉峰, 张耀存. 基于概率加权估计的中国极端气温时空分布模拟试验. 大气科学, 2004, 28, (5): 771–782. |
| [22] | 丁裕国, 郑春雨, 申红艳. 极端气候变化的研究进展. 沙漠与绿洲气象, 2008, 2, (6): 1–5. |
| [23] | 陈兴旺. 广义极值分布理论在重现期计算的应用. 气象与减灾研究, 2008, 31, (4): 52–54. |
| [24] | 欧进萍, 林迟. 基于结构全寿命设计需求的哈尔滨地区气温统计分析. 自然灾害学报, 2009, 18, (2): 4–14. |
| [25] | Box G E P, Cox D R. An analysis of transformations. J Roy Statist Soc (Ser B), 1964, 26: 211–252. |
| [26] | Buchinsky M. Quantile regression, Box-Cox transformation model, and the U S wage structure, 1963—1987. Journal of Econometrics, 1995, 65: 109–154. DOI:10.1016/0304-4076(94)01599-U |
| [27] | 薛跃, 盛党红. Box-Cox变换原理及其在财务比率正态分布中的作用. 南京理工大学学报, 2005, 29, (5): 627–630. |
| [28] | 吕纯濂, 陈舜华. 带有变量中误差非正态模型中的Box-Cox变换. 南京气象学院学报, 1997, 20, (1): 85–90. |
| [29] | Bonsal B R, Zhang X B, Vincent L A, et al. Characteristic of daily and extreme temperature over Canada. J Climate, 2001, 14: 1959–1976. DOI:10.1175/1520-0442(2001)014<1959:CODAET>2.0.CO;2 |
 2011, 22 (2): 145-151
2011, 22 (2): 145-151



