气候变化及其伴生的极端天气气候事件变化对经济社会发展有诸多不利影响。近年来，各国科学家对极端天气气候事件变化给予了越来越多的关注。特别是近年来我国夏季高温热浪频发，盛夏高温严重影响人们的生产和生活，并带来重大的国民经济损失，因此极端温度的研究一直倍受关注。国外许多专家针对美国、加拿大和日本等区域的极端气候事件进行了深入研究^[1-3]。国内专家对极端气温的研究也很多，任福民等^[4]、翟盘茂等^[5]研究了我国年、季极端气温变化趋势的时空特征，以及我国北方近50年温度极端事件变化。严中伟等研究了近几十年我国极端气候变化格局^[6]，很多学者研究了我国及部分地区年、季极端气温变化趋势的时空特征^[7-13]，张勇等^[14]还利用Hadley中心的模型展望了未来我国极端温度事件变化情景。但是，关于我国极端高温事件阈值指标的研究多借鉴国外现有算法，考虑到我国极端高温本身概率分布特征的并不多见。因此，针对我国极端高温事件阈值分布的规律性进行研究对探讨我国极端气候事件有重要意义。

国内外关于极端高温事件的指标有高温日数和一年中高温日持续在6 d以上的时段数，高温日数定义为最高气温值大于某固定阈值的天数。阈值有使用绝对值进行定义，例如使用35℃，38℃和40℃作为阈值^[15]；为了不同地区能够相互比较，最多见的是采用某个百分位值作为阈值，超过这个阈值被认为是极端气候事件。关于高温阈值，一般使用温度序列的第90百分位值作为极端值的阈值，但具体阈值划分和计算方法各种各样^{[13, 15-16]}，方法的合理性值得研究。本文将针对有关最高气温阈值的计算、极端气候事件阈值的确定以及阈值的全国分布等问题进行研究。

本文所用的最高气温资料取自国家气象信息中心，资料为1951年1月1日—2008年12月31日，均为全国基本和基准气象站资料，超过700个站。取1961年1月1日及2008年12月31日均有资料的站点，共计250个站，但其中仍有缺测情况，详见表 1。

表 1

表 1 我国最高气温资料集中资料缺测日数与站数 Table 1 The number of stations and data missing days in daily maximum temperature dataset 日数范围/d 站数 比例/% 0 117 47 1~3 82 33 4~6 20 8 7~10 5 2 11~365 14 5 ＞366 12 5

表 1 我国最高气温资料集中资料缺测日数与站数 Table 1 The number of stations and data missing days in daily maximum temperature dataset

由表 1可知，89.6%的测站缺测在10 d以内，包含224个站逐日最高气温资料。为了计算方便，首先对其中缺测资料进行恢复。

在资料恢复试验中，多利用相邻站作为需要恢复站点 (对象站) 的参考站，使用回归和判别分析方法进行插值和恢复^[17-19]，但由于通常同一地区测站密切相关，在用相邻站与对象站作多元回归和判别分析中，回归方程和判别方程会出现病态，使得方程不稳定，从而影响资料恢复的效果，而偏最小二乘回归方法可以克服这方面缺点，对上海地区的缺测资料恢复试验表明，偏最小二乘回归方法对于这种高相关性的站点之间的资料插补效果较好^[20]。

为了进行缺测资料恢复效果比较，选取若干站，检验缺测资料标准化恢复值的估计值_zj与实测值y_zj之差，并计算其均方根误差^[21]：

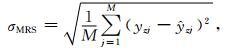
(1)

式 (1) 中，M为检验的站数。

确定使用的恢复方法后，恢复时使用标准距离选取6个相邻站，由于原资料已经过均一化和质量控制，相邻站气温序列均满足质量要求^[20-21]。

进行偏最小二乘回归分析的恢复中，由于6个相邻站相关性很好，故仅选取由它们构成的因子场的第1主分量进行恢复。表 2给出12个月最高气温100个测站恢复检验的均方根误差比较。

表 2

表 2 恢复最高气温检验的均方根误差比较 (单位：℃) Table 2 Mean root squire error for interpolated maximum temperature data (unit: ℃) 月份 平均值 均方根误差 1 1.10 0.37 2 1.10 0.49 3 1.04 0.26 4 1.46 0.42 5 1.63 0.46 6 2.23 0.27 7 2.59 0.51 8 2.56 0.83 9 2.16 0.62 10 1.48 0.47 11 1.26 0.56 12 1.14 0.32

表 2 恢复最高气温检验的均方根误差比较 (单位：℃) Table 2 Mean root squire error for interpolated maximum temperature data (unit: ℃)

从表 2各月恢复效果看，除夏季外，其他季节气温恢复效果很好，即使是夏季，也与单站月资料恢复效果相当 (与文献[19]结果比较)。

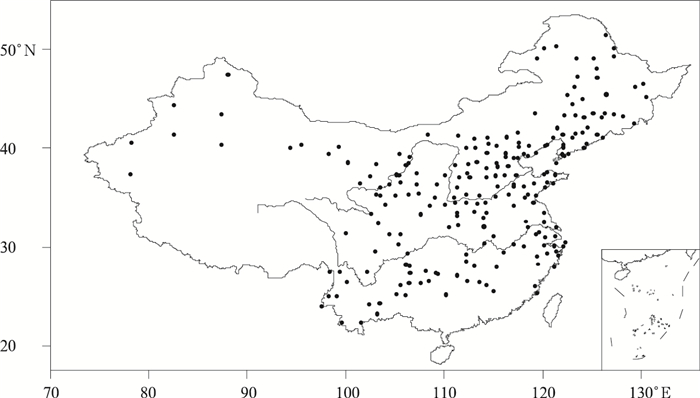
图 1给出本研究所用资料集的我国最高气温站点的地理分布。由图 1可知，选取的站点覆盖我国大部分地域，基本可以反映我国的最高气温气候的地理分布。

图 1

图 1. 我国最高气温站点的地理分布 Fig 1. The geographical distribution for maximum temperature stations in China

较为多见的是采用某个百分位值作为极端气候事件的阈值 (以下简称为阈值)。计算阈值的常用方法有以下两种。

方法1 将本文统计时段内某站逐日的气温序列，按大小升序排列，得到x₁，x₂，…，x_n，则百分位数为^[15]

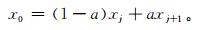
(2)

式 (2) 中，j=[p(n+1)], a=p(n+1)-j。j为降水量记录按大小升序排列后的序号；p为百分位值对应的概率；方括号表示数值取整；n为序列样本容量。

方法2 对气温序列处理与方法1类似，仍然将序列按大小升序排列，得到的升序序列，某个值小于序号为j对应的事件出现的概率为^[22-23]

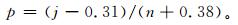
(3)

式 (3) 中，j为升序排列后的序号，如果n=30，第90百分位数对应的排序序号为27，按均匀分布，概率值应为27/30×100%=90%。因此，对应的气温值称为第90百分位值。如果取1年的气温序列，记录有365个值，那么第90百分位上的值，为排序后的328位置的气温 (理论计算概率值为89.9%) 和329位置的气温 (理论计算概率值为90.2%) 中间的线性插值，可以得到p=90%对应的百分位值。这一计算相当于仍然使用式 (2)，只需要将排列后的序号的计算改为

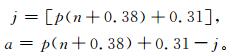
(4)

上述计算阈值的方法是基于气温变量遵从均匀分布。我国各站的最高气温是否遵从均匀分布，需要进行检验。对一个气温序列x₁，x₂，…，x_n，若遵从均匀分布，其数学期望和方差分别应该为

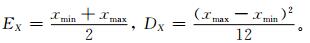
(5)

式 (5) 中，x_min，x_max分别为序列最小值和最大值。要检验最高气温总体是否来自均匀分布，可以检验实际气温序列的期望是否与均匀分布期望有显著差异。检验的统计量为^[24]

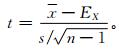
(6)

其遵从自由度为n-1的t分布。式 (6) 中，x，s分别为序列平均值和标准差；n为序列样本容量；E_X为均匀分布期望。

对夏季 (6—8月) 逐年224站的最高气温序列进行显著性检验，序列的样本数n=92。计算发现，平均74%的测站有显著差异 (显著性水平为0.05)，有显著差异站点占全部站点比例最大的年份 (1997年) 达到88%，最小的年份 (1988年) 也能够达到63%。尤其值得注意的是，大部分台站的概率分布并不遵从均匀分布。进一步计算逐年各站最高气温的夏季序列的偏度系数^[25]，也发现大部分台站的概率分布为负偏度。说明我国夏季最高气温序列大部分台站既不遵从均匀分布，也不遵从正态分布。因此，我国最高气温序列一般不能用均匀分布或正态分布来处理，即严格地说，使用传统计算方法计算阈值并不适合。

在最高气温序列百分位阈值确定中，为了克服传统计算方法带来的弊端，本文提出按日最高气温遵从的实际概率分布来确定百分位阈值。计算时首先对某站某年份的气温序列，确定样本频率分布的组数G。组数按照下式确定^[25]

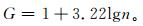
(7)

实际序列样本容量n =92，近似取为100，计算得到的组数G=7.44，最后组数取为7。求得变量的频率分布后，再利用累积频率分布便可确定百分位阈值。即将第90百分位与按分组后各组的累积频率值相比较，落入某两组的累积频率值时，采用线性插值求取第90百分位值，即为方法3。

传统方法1和方法2计算得到的阈值没有很大差异，但使用方法3所得到的阈值与它们相比较，一般有1℃以上的差异。以1997年为例，3种方法求得的高温阈值分别为39.3℃，39.3℃和40.5℃。表 3列出1997年224站夏季气温序列用3种不同方法得到的高温阈值的比较。

表 3

表 3 1997年夏季气温序列不同方法求取高温阈值的比较 (单位：℃) Table 3 The threshold values by 3 methods for summer temperature in 1997 (unit: ℃) 统计量 方法1 方法2 方法3 最大值 39.3 39.3 40.5 最小值 21.1 21.0 22.1 平均值 33.3 33.3 34.7

表 3 1997年夏季气温序列不同方法求取高温阈值的比较 (单位：℃) Table 3 The threshold values by 3 methods for summer temperature in 1997 (unit: ℃)

由表 3可知，方法1与方法2的阈值差别很小。而方法3与它们相比较，平均值差值超过1℃。实际上，使用3种方法得到的224站阈值序列，对任意两个时间序列阈值平均值，可以做差异的显著性检验，检验统计量可以取^[24]

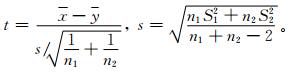
(8)

式 (8) 中，x，y，S₁，S₂分别为两个时间序列平均值和标准差，n₁，n₂分别为两个时间序列样本容量。对1997年夏季气温序列3种方法求取高温阈值计算发现，方法2与方法1比较，224站阈值平均值差异不显著。而方法3与方法1相比较，则有显著差异，其t值达到4.49，超过0.05显著性水平。

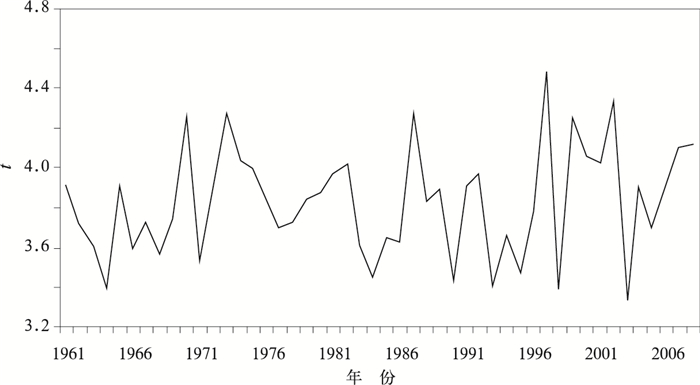
图 2给出了利用方法3与方法1计算我国224站夏季高温阈值平均值差异检验统计量t值的逐年变化。

图 2

图 2. 方法3与方法1的阈值平均值差异检验统计量t值的逐年变化 Fig 2. Annual differences of statistical values t calculated by Method 3 and Method 1

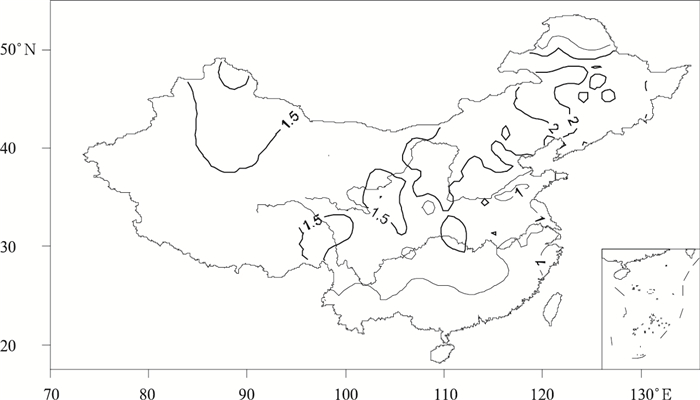
由图 2可知，各年份夏季序列全国高温阈值平均值，方法3与方法1的差异显著，其t值的逐年变化不大，最小值为3.33，最大值为4.49，此变化范围均超过0.05显著性水平。而方法2与方法1的差异不显著，最小值为-0.16，最大值为-0.10。说明本文提出的高温阈值计算方法所得到的阈值，与传统的阈值计算有显著差异。由于方法3与方法1的阈值平均值差异最大值出现在1997年，图 3给出利用方法3与方法1计算得到的1997年全国台站阈值差值的分布。

图 3

图 3. 1997年方法3与方法1计算的阈值差值的分布 (单位：℃) Fig 3. The geographical distribution for differences of thresholds calculated by Method 3 and Method 1(unit: ℃)

由图 3可见，差值较大的地方出现在我国东部，这是我国经济发达和城市人口集中的区域。作为最高气温气候事件的阈值，应该接近日常人们使用的最高气温 (即35℃) 的标准。计算发现，方法1、方法2和方法3超过35℃的阈值站数占总站数的比例，分别为24%，23%和38%。显然方法3更接近实际人们使用的标准。

一般以30年的平均值确定为气象要素极端气候事件的阈值^[19]。以30年作为滑动气候阶段样本，例如，选取1951—1980年，1952—1981年，直到1979—2008年的第19个滑动气候阶段的样本。为了比较气候阶段的阈值代表性，使用所有气候阶段平均阈值的离散度^[22]来度量。即

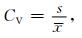
(9)

式 (9) 中，x和s分别为阈值在气候阶段中的平均值和标准差，显然C_V的量纲为1，便于不同地区的比较。C_V值大，表明气候阈值在各个气候阶段内变化幅度大，极端气候事件的阈值代表性差。一般C_V应小于1，若C_V＞1，则表示阈值变化的平均幅度比平均值大，即阈值的代表性较差。

对我国夏季最高气温序列按上述期间计算所有气候阶段平均阈值，结果发现使用方法3的气候阶段平均阈值的离散度为0.10，说明其气候阈值有代表性。表 4给出我国224站中夏季气温气候极端事件的阈值在最大值、最小值、平均值和大于35℃站数占所有气候阶段、站点比例的比较。

表 4

表 4 我国夏季气温气候极端事件阈值的比较 Table 4 The threshold values of climate extremes by 3 methods for summer temperature 项目 方法1 方法2 方法3 最大值/℃ 39.7 39.7 41.0 最小值/℃ 20.8 20.8 22.1 平均值/℃ 34.0 33.9 35.3 大于35℃站点所占比例/% 40 38 57

表 4 我国夏季气温气候极端事件阈值的比较 Table 4 The threshold values of climate extremes by 3 methods for summer temperature

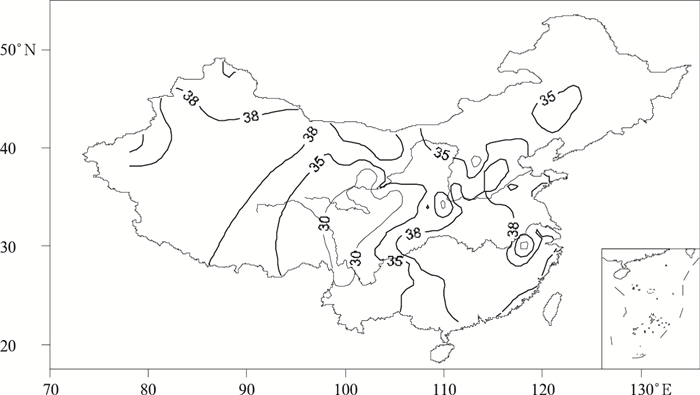
由表 4可知，在3种计算阈值方法中，只有方法3计算得到气候极端事件的阈值，224站的平均值能够达到35℃，大于35℃站数所占比例也最大，与日常人们使用的最高气温灾害阈值相接近。同时，气候阈值比个别年份的阈值，与日常人们使用的最高气温灾害阈值更接近，进一步说明气候阈值合理性。图 4给出使用方法3得出的夏季气温气候极端事件阈值的全国分布。

图 4

图 4. 我国夏季最高气温极端气候事件的阈值分布 (单位：℃) Fig 4. The distribution for threshold values of climate extremes in summer (unit: ℃)

由图 4可见，我国大部分地区，除西南、青海、东北大部和内蒙古外，最高气温极端气候事件的阈值均超过35℃。进一步说明人们日常使用的35℃高温阈值作为夏季高温事件标准合理。

本文在对1961—2008年我国224站最高气温资料进行整理的基础上，选取相邻站，用偏最小二乘法对缺测资料进行恢复，建立了较为完整的逐日最高气温资料集。用3种计算阈值的方法，对确定我国最高气温阈值进行计算比较研究，结果如下：

1) 用不同方法计算高温阈值的试验结果表明：本文提出根据最高气温的实际样本频率分布作为实际概率分布的近似，较传统求极端气候事件阈值的方法效果更好。

2) 使用30年气候阶段样本确定的我国最高气温气候极端事件阈值，能够比较接近日常使用的极端气候事件阈值，具有较好的稳定性和代表性。

3) 我国大部分地区，除西南地区、青海、东北地区大部和内蒙古外，最高气温极端气候事件的阈值均超过35℃，说明日常人们使用的35℃高温阈值作为夏季高温极端事件的标准合理。