在全球气候变化和人类活动的共同影响下，全球极端天气气候事件呈现出强度大、频次高、影响范围广等特点^[1]，近年来极端事件的发生给社会、经济和人民生活造成了严重的影响和损失。有关极端天气气候事件的变化已引起科学家们的高度关注，国内外对极端天气气候事件的研究主要集中在降水和温度的历史观测资料诊断分析与预估两个方面^[2-8]，较少涉及预测特别是短期气候预测方面。

在短期气候预测业务中，降水预测既是重点又是难点，倍受人们的关注，极端降水的预测则更为困难。目前动力气候预测模式已成为气象工作者的重要工具，在气候预测业务中得到广泛应用^[9-10]。但动力气候模式对大尺度环流的特征模拟较好，对空间尺度较小的降水、气温等地表气候要素的预测技巧较低^[11]。因而如何利用预测效果较好、技巧较高的大尺度模式信息用于降水、气温等中小尺度预报，降尺度方法就显得十分重要^[12]。近年提出的统计降尺度技术 (Statistical Downscaling, SD) 则能利用气候模式输出的具有较高预测技巧的大尺度信息，生成高时空分辨率的模拟序列，应用于气候预测、气候变化等方面，并取得了一系列成果，但这些工作主要用于月、季气候距平的预测^[13-15]或者极端事件模拟^[16-17]，而缺少极端事件预测信息，因此探讨统计降尺度方法在短期气候预测特别是极端气候事件预测方面的应用具有重要意义。

国家气候中心业务化的月动力预测气候模式 (DERF) 在短期气候预测特别是月尺度气候预测中发挥着重要作用。但该模式水平分辨率较粗，且日预测可信度较低，导致区域尺度或日尺度降水预测准确率偏低。考虑到统计降尺度方法的特点，将其引入区域降水预测和极端降水日数预测，对DERF输出进行统计降尺度处理，以期得到高时空分辨率的预测信息。

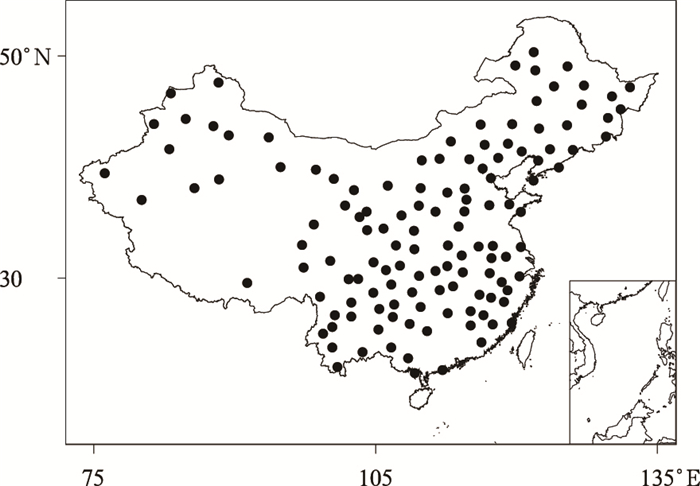
观测数据为国家气象信息中心提供的1961—2008年的20：00—20：00(北京时，下同) 站点逐日降水量，在此基础上计算预测起报日起1~10 d，11~20 d，21~30 d，31~40 d的旬降水量和1~30 d，11~40 d的月降水量, 并利用逐日降水数据逐年统计相应时段内的极端降水日数。然后分别以旬、月降水量和极端降水日数作为预报量建立统计降尺度模型。由于160个站中有133个站点逐日观测数据序列能够满足建模要求，因此只针对这些站点建模，图 1给出了各站点地理位置。

图 1

图 1. 气候观测站点地理位置 Fig 1. Location of climate stations

DERF数据为1982—2008年以来的回算和实时预测的逐候滚动的未来40 d的候平均200 hPa位势高度场 (H200)、500 hPa位势高度场 (H500)、700 hPa位势高度场 (H700)，200 hPa纬向风场 (U200)，700 hPa纬向风场 (U700)，200 hPa经向风场 (V200)，700 hPa经向风场 (V700)，海平面气压场 (SLP)。建模时，首先在候平均资料基础上分别计算6个预测时段的各时段平均值，计算时取每个时段回算或预测的集合平均值，集合成员最多40个，水平分辨率为2.5°×2.5°。

NCEP/NCAR再分析资料^[18]为每年72个候的候平均数据，由基于每天4个时次的数据处理而成，环流因子与NCEP相同，水平分辨率为2.5°×2.5°。建模时也需要首先在整理好的候平均数据基础上分别计算各环流因子每个预测时段的平均值。

关于极端降水的定义可分为绝对值和相对值两种，考虑到降水的区域性和季节性差异，采用相对指标来定义极端降水。根据WMO气候委员会 (CCI)/全球气候研究计划 (WCRP) 气候变化与可预测性计划 (CLIVAR) 气候变化检测、监测和指标专家组 (ETCCDMI) 有关定义和计算方法^①，将极端降水日数定义为时段内日降水量大于第90个百分位值的天数。每个站点逐月计算第90个百分位数，即对1971—2000年每个月内超过1 mm的降水量从小到大进行排序，计算第90个百分位对应值，作为极端降水量阈值。

① http://www.clivar.org/organization/etccd.

采用两步法和一步法两种降尺度方法预测极端降水日数，其中一步法以极端降水日数为预报量，与其高相关的DERF大尺度环流场为预报因子。两步法首先以降水距平百分率为预报量，然后以此作为控制条件，从随机天气发生器生成的逐日降水随机序列选择满足该给定条件的降水，计算极端降水日数。

综合动力模式预测与统计降尺度两种方法的优势，利用国家气象信息中心提供的我国133个站逐日降水资料、NCEP/NCAR再分析资料和DERF的回报资料，将DERF提供的具有较高预测技巧的大尺度信息统计降尺度到各观测站点，预测极端降水日数。

预报因子的选择是建立统计降尺度模型过程中一个非常重要的环节，不同的大尺度气候预报因子对预报量的模拟结果具有很大影响，对于不同季节、不同站点来说，其最优预报因子类型及其地理位置是不同的^[19-20]。首先，对每个观测站点及预测时段分别计算预报量与模式输出和NCEP再分析资料两种大尺度环流量之间的相关系数。然后在全球范围内搜索两种相关系数均达到0.05显著性水平的区域，并保证连通区域面积大于4×4网格点，最后将所有满足以上条件的区域代表性格点挑选出来，按照相关系数的大小进行排序，挑选前8个作为预报因子集，这样既保证了预报因子与预报量之间的强相关性，又保证了预报因子能够被DERF模式在较大的区域内准确地模拟出来。具体计算步骤如下。

① 逐站分别计算预报量与DERF和NCEP再分析资料各大尺度因子H200, H500, H700, U200, U700, V200, V700和SLP各格点的相关系数。

② 给定显著性水平，判断格点 (i, j) 及与之相邻的4个格点的相关系数是否均通过显著性检验，且与NCEP和DERF的相关系数同号，若符合这一条件，该点赋值为1，否则赋值为0。

③ 在② 的基础上，计算格点 (i, j) 邻近4个格点的平均值，作为 (i, j) 点的值。

④ 判断点 (i, j) 处的值是否大于周围80个格点的值，如果小于其中某个格点值，则赋值为0，否则保持原值不变，作为选取关键区的指标。

⑤ 对每个环流场全球所有网格点的非零关键区指标值从大到小排序，计算非零关键区个数。

⑥ 计算8个环流场所有非零关键区个数总和，如果数值小于7，转入⑦，如果大于8，转入⑧。

⑦ 选取所有非零关键区所在格点处的环流值作为预报因子。

⑧ 首先取每个环流场相关系数最高的格点作为预报因子，然后再依次从每个环流场选取相关系数次高的格点作为预报因子，依此类推，直到预报因子达到要求为止。预报因子选取流程见图 2。

图 2

图 2. 预报因子选取示意图 Fig 2. Scheme of predictor selection

这样，每个站点最大预报因子个数为8。

最后，利用最优子集回归方法和双评分准则，建立DERF模式的大尺度预报因子与站点极端降水日数的转换函数，预测延伸期旬、月内出现的极端降水日数。相似的方法已成功应用于站点月降水量的预测^[13]。

考虑到DERF与NCEP再分析资料的平均值和标准差的系统误差，对预报量和环流因子进行标准化处理后再进行建模。由于DERF回算资料较短，采用1982—2006年的DERF回算资料建立最优子集回归 (OSR) 模型并进行交叉检验，2007—2008年的DERF回算资料进行独立样本检验。

随机天气发生器 (WG) 是一种时间降尺度方法，国内外许多研究将GCMs与天气发生器技术相结合，用于研究气候变化对极端气候事件，农业生产、水土保持、水量与水质的潜在影响^[21-24]，可以提前几个月甚至1年为有关管理者提供决策信息支持。单纯的WG是根据历史观测序列计算相应的参数，生成的随机序列具有气候统计意义，并不能直接用于预测。为了充分利用DERF模式预测信息，并结合WG生成逐日序列的特点，提出两步法的概念用于极端降水日数预测，该方法曾成功应用于35℃高温日数的预测^[25]。

第1步以时段降水量为预报量，采用与2.1节相同的方法确定预报因子，然后应用OSR方法对DERF输出的大尺度环流信息进行降尺度，预测各站点降水距平百分率。用DERF回报的1982—2006年的资料进行交叉检验，2007—2008年资料进行独立样本检验。另外对DERF输出降水进行双线性插值处理，用于评估统计降尺度方法相对于模式直接预测的增值效应，说明其应用价值。

第2步应用国家气候中心开发的随机天气发生器 (BCCWG_V2.1) 生成逐日降水随机模拟序列^[17]，以第1步预测的降水距平百分率为控制条件，统计随机序列中满足设定条件的极端降水出现频率。

首先利用1961—2000年逐日气候观测数据计算BCCWG_V2.1天气发生器模型参数，包括降水转移概率矩阵，降水分布参数值，然后应用Monte-Carlo方法生成10000个逐日降水随机序列。在此序列和预测降水距平百分率基础上，依据以下两个条件计算极端降水日数：① 如果模拟降水距平百分率 (P_sim) 落于区间[x₁×P_pred，x₂×P_pred]，则记为极端事件发生年，并统计该时段内超过极端降水阈值的日数。② 统计极端事件发生年数 (记为n) 和极端事件发生日数 (记为N)，如果n超过100，则极端事件日数为预测时段天数×N/n。否则，极端事件日数记为0。x₁，x₂为降水距平百分率倍数，P_pred为预测的降水距平百分率。应用数值试验的方法，通过比较不同x₁，x₂取值时的预测结果与历史观测极端日数，最终确定合理的x₁，x₂值。

从BCCWG_V2.1模拟的10000个随机模拟序列中计算预测时段内超过极端阈值的发生频率，然后换算为预报时段内极端降水日数，称为WG随机预测，作为统计降尺度方法的参考，用于评估统计降尺度方法的有效性和增值效应。

针对两步法中的降水量预测，采用预报评分 (P)、随机技巧评分 (RATc)、气候技巧评分 (CLTc)、距平相关系数 (ACC) 和异常级预报评分 (TS)5种业务评分^[26]和对其进行评估。针对极端降水日数的预测，采用异常级评分对其评估。表 1列出了评估的预测量和相应的预测方法。

表 1

表 1 预报量及预测方法说明 Table 1 Description of predictants and predictors 预报量 方法名称 方法描述 降水量 方法1 方法2 OSR统计降尺度 模式直接预测 极端降水日数 方法3 方法4 方法5 一步法 两步法 WG随机预测

表 1 预报量及预测方法说明 Table 1 Description of predictants and predictors

应用标准差 (σ) 的概念对极端降水日数进行评估，首先利用建模所用的预测时段内极端降水日数序列计算标准差，然后根据表 2将预测和观测的极端降水日数转化成为六级概念，再计算实况与预报之差，根据表 3进行评分。对每个站点分别计算分值，所有站点平均值即为最终的异常级评分。

表 2

表 2 极端日数分级 Table 2 Classification of number of extreme precipitation days 分级文字描述 分级量化描述 分级标准 特多 3 >1.0σ 偏多 2 0.3σ~1.0σ 正常略多 1 0~0.3σ 正常略少 -1 -0.3σ~0 偏少 -2 -1.0σ~-0.3σ 特少 -3 < -1.0σ

表 2 极端日数分级 Table 2 Classification of number of extreme precipitation days

表 3

表 3 异常级评分表 Table 3 Abnormal class score 观测与预测异常级之差 0 -1或1 -2或2 -3或3 -4或4 -5或5 -6或6 评分 100 80 60 40 20 0 0

表 3 异常级评分表 Table 3 Abnormal class score

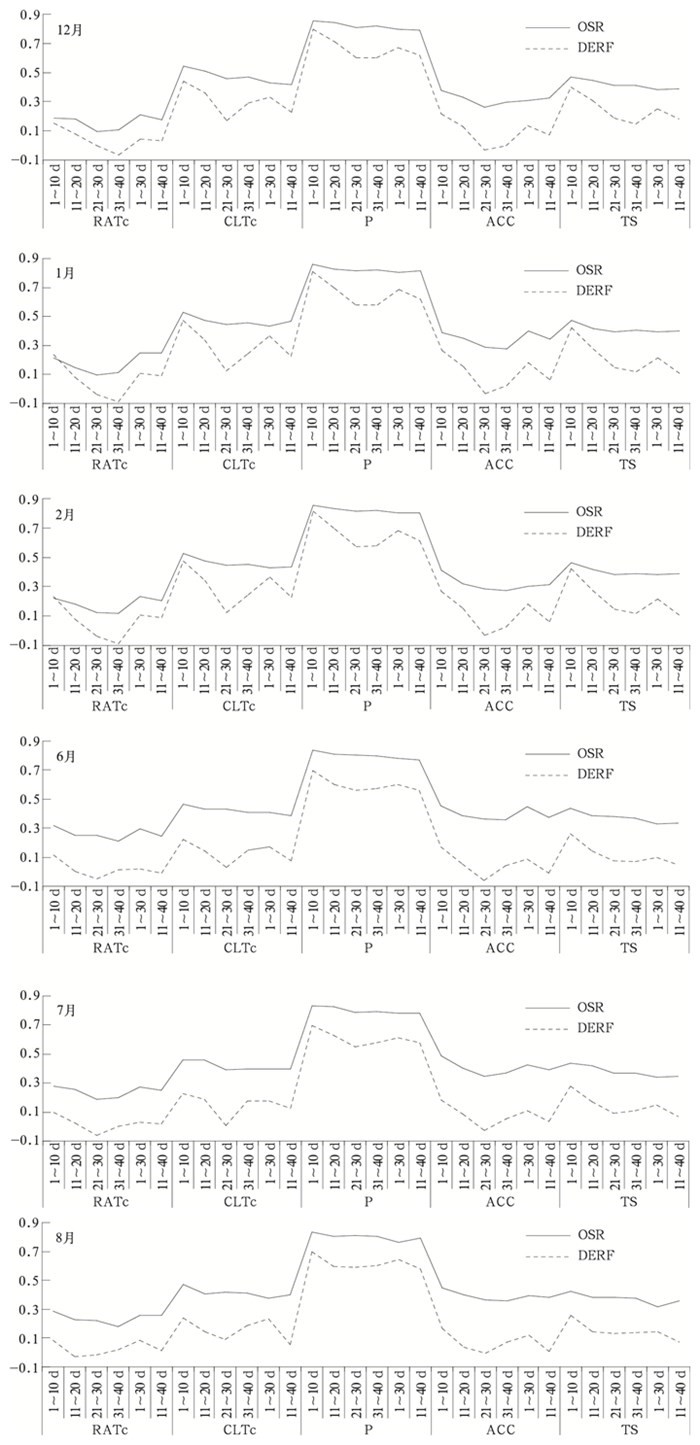
本文重点分析夏、冬两季每月1日起未来6个时段旬或月降水量的预测效果，图 3给出了5种业务评估指标1982—2006年交叉检验平均值的变化曲线。为了与其他几种评估指标保持单位一致，仅在图 3中将P评分值乘0.01换算为0~1之间的值。可以看出，相对于随机预测和气候预测，OSR统计降尺度方法的预测技巧评分均为正值，而模式直接预测则有正有负。OSR方法的异常级评分超过0.3，模式直接预测除1~10 d外，其他几个时段的异常级评分低于0.3。OSR方法的P评分在75~80之间，模式直接预测P评分除第1个时段较高外，其他几个时段均低于70。分析表明，与模式直接预测相比，OSR统计降尺度方法可显著提高降水量预测技巧，特别是后面几个预测时段，预测效果改善更为明显。

图 3

图 3. 5种业务评分的降水距平百分率交叉检验结果 Fig 3. Crossing validation of precipiation anomaly pertange for 5 kinds of operational scores

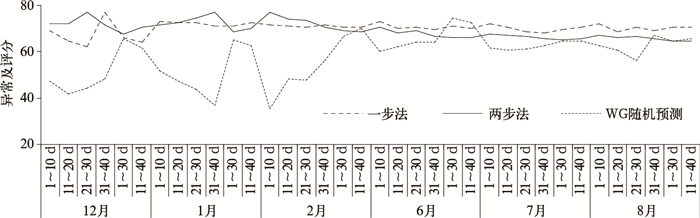
图 4给出了极端降水日数交叉检验异常级评分1982—2006年的平均值，可以看出两种统计降尺度方法的评分在60~80之间，大部分优于WG随机预测，冬季WG随机预测效果最差。其中一步法比较稳定，冬、夏两季变化不大。两步法对冬季极端降水日数的预测略优于一步法，一步法对夏季极端降水日数的预测略优于两步法。从预测时效看，两种统计降尺度方法均随时间后延预测技巧略呈下降趋势。

图 4

图 4. 极端降水日数交叉检验异常级评分 Fig 4. Abnormal class score of crossing validation for day number with extreme precipiation

为了进一步分析造成两种方法预测技巧差异原因，统计计算了1982—2006年每月1日起测的1~30 d内极端降水日数多年区域平均值，其中冬季12, 1, 2月依次为0.26 d，0.37 d，0.46 d；夏季6, 7, 8月依次为1.00 d，0.99 d，0.91 d；夏季极端降水日数出现频率明显多于冬季。分析认为当极端事件出现频率较高时，两步法还存在改进空间，可以通过改变判断极端降水事件发生的控制条件，即OSR降水距平百分率预测结果与天气发生器随机模拟序列的结合方式，今后将围绕这一问题进一步展开研究。

表 4列出了2007年和2008年夏、冬两季每月1日预测的1~30 d, 11~40 d两个时段的月降水量距平百分率预报评分P。除12月1日和1月1日两次预测，P评分表明OSR预测技巧高于DERF直接预测。

表 4

表 4 2007年和2008年夏、冬两季每月1日起测的月降水量距平百分率P评分 Table 4 P score for monthly precipiation anomaly percentange predicted on the first day of a month during summer and winter in 2007 and 2008 起测日期 预测时段/d OSR统计降尺度 模式直接预测 2007年 2008年 2007年 2008年 12-01 1~3011~40 6569* 7070* 6755 8169 01-01 1~3011~40 6970 7285* 7074 7865 02-01 1~3011~40 84*91* 80*77* 5655 7055 06-01 1~3011~40 70*69* 65*77* 5451 5245 07-01 1~3011~40 70*64* 5771* 5750 5949 08-01 1~3011~40 71*76* 7376* 4349 7463 注：*表明OSR统计降尺度预测技巧高于模式直接预测。

表 4 2007年和2008年夏、冬两季每月1日起测的月降水量距平百分率P评分 Table 4 P score for monthly precipiation anomaly percentange predicted on the first day of a month during summer and winter in 2007 and 2008

表 5给出了极端降水日数异常级评分的2007年和2008年的平均值。两种方法评估结果表明，对于这两年冬、夏季几个月的预测，均是两步法预测技巧高于一步法，大部分评分在60左右，与交叉检验多年平均值相当。

表 5

表 5 2007—2008年平均的夏、冬两季每月1日起测的极端降水日数异常级评分 Table 5 Abnomal class score for day number with extreme precipiation predicted on the first day of a month during summer and winter averaged of 2007 and 2008 起测日期 12-01 01-01 02-01 06-01 07-01 08-01 预测时段/d 1~30 11~40 1~30 11~40 1~30 11~40 1~30 11~40 1~30 11~40 1~30 11~40 两步法 58 57 66 65 65 61 62 56 64 56 61 52 一步法 38 28 33 22 40 29 39 18 35 24 41 28

表 5 2007—2008年平均的夏、冬两季每月1日起测的极端降水日数异常级评分 Table 5 Abnomal class score for day number with extreme precipiation predicted on the first day of a month during summer and winter averaged of 2007 and 2008

用OSR统计降尺度方法对DERF预测的大尺度信息进行降尺度处理，用1982—2006年的数据进行交叉建模检验，用5种评估指标进行评估，利用2007年和2008年数据进行独立样本检验。在此基础上用两步法和一步法分别预测极端降水日数，采用异常级评分对两种方法的预测技巧进行分析比较。通过分析比较，得出如下结论：

1) OSR统计降尺度方法的预测技巧明显高于模式直接预测的降水距平百分率，特别是11 d以后几个时段的预测。OSR方法的异常级评分超过0.3，模式直接预测除1~10 d外，其他几个时段的异常级评分低于0.3。OSR方法的P评分在75~80之间，模式直接预测P评分除第1个时段较高外，其他几个时段均低于70。

2) 两步法与一步法均优于WG随机预测。统计降尺度方法异常级评分在60~80之间，高于WG随机预测。从预测时效看，两种统计降尺度方法均随时间后延预测技巧略呈下降趋势。交叉检验结果表明：对于极端降水日数发生频率偏少的冬季，两步法预测技巧略高于一步法，而对于极端降水日数发生频率偏高的夏季，一步法预测技巧略高于两步法。

研究结果表明：基于DERF的OSR统计降尺度方法对于降水量预测具有较高预测技巧，能显著提高模式对于降水的预测。对于极端降水日数的预测，两种统计降尺度方法均具有一定的预测技巧，但需要在今后应用中不断总结以进一步改进完善。在用于短期气候预测时，可参考交叉检验评估结果，重点参考预测技巧高的区域和时段的结果。