高时空分辨率静止卫星可以用作识别大气中正在发生的动力和热力过程的有效指示, 可以监测小到单个对流云团, 大到行星尺度天气系统的发生、发展和演变[1]。但一个严重问题却阻碍了卫星资料的进一步应用, 那就是浩大的资料量与相对狭小的存储空间之间的矛盾, 如何对云图资料进行有效压缩存储已成为一个亟待解决的问题。气象卫星云图压缩属于图像压缩范畴, 图像的有失真压缩一般使用基于离散余弦变换 (DCT) 的JPEG方法, 但JPEG图像在大压缩比时, 往往会在水平和垂直方向出现晕圈、幻影, 产生“方块"效应, 这是因为对原始图像进行了分块的DCT变换和量化。如果不分块或分块很大而进行DCT变换与量化, 那么图像块中像素能量集中到少量系数, 效果将变得不明显, 即不利于对数据进行量化压缩, 同时还使得计算复杂度增加。
为了克服JPEG图像的缺点, 获得更好的压缩效果, 人们开始尝试用小波变换 (wavelet trans-form) 方法对图像进行压缩处理。1980年法国科学家Morlet在分析地震波高频成分时, 首先提出了小波变换, 引起了极大关注[2]。此后二十多年, 小波变换理论得到迅速发展, 并成为应用数学发展的一个新领域。小波变换技术是一种时间尺度分析方法, 具有多分辨率分析的特点, 而且在时频两域都具有表征信号局部特征的能力[3]。利用小波变换可以一次变换整幅图像, 不仅可以达到很高的压缩比, 而且不会出现JPEG重建图像中的“方块"效应[4]。
近年来, Mallat[5], Taubman等[6], Xiong等[7]先后利用小波变换方法对图像进行了压缩试验, 取得了很好的效果。但是, 目前在小波压缩的研究中, 大都使用接近于自然图像的Lena, Barbara等进行试验, 而气象卫星云图在图像灰度分布和小波系数分布等方面都与自然图像存在差异, 在实际压缩方案设计中必须予以考虑。利用卫星云图的特点, 获得较好压缩效果是本文的研究重点。
1 图像小波压缩原理及卫星云图特征 1.1 小波变换的快速算法小波变换是时间和频率的局域变换, 其基本思想是以小波函数为基底对信号进行分解, 根据信号属性可分为连续小波变换和离散小波变换[4, 8-11]。图像压缩采用离散小波变换, 通常使用Mallat提出的求解小波系数的快速塔形算法。该算法可以使离散小波变换以数字滤波器组的形式实现, 其小波分解公式为:
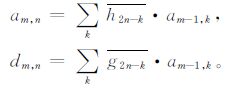
|
(1) |
同样, 有Mallat快速重构算法, 即
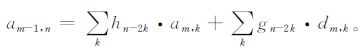
|
(2) |
其中, am, n表示信号的模糊分量, dm, n表示信号的细节部分。hn, gn分别表示低通滤波器和高通滤波器, 令hn=h-n, gn=g-n。
将小波变换由一维推广到二维, 就可适用于图像处理。二维图像的小波分解算法如下:
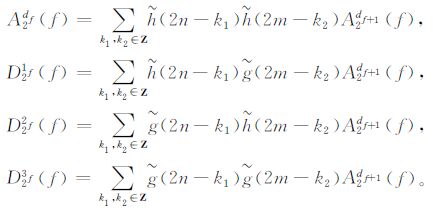
|
(3) |
其中, A2df(f) 表示A2df+1 (f) 的低频分量, D21f(f) 给出了A2df+1(f) 在y方向上的高频分量、D22f(f) 给出了x方向上的高频分量、D23f(f) 给出了x和y方向都是高频的分量。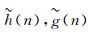
同样, 也可以通过A2df(f), D21f(f), D22f(f), D23f(f) 重构A2df+1(f):
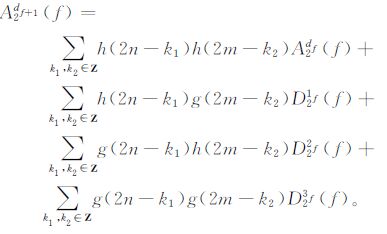
|
(4) |
小波变换用于图像编码的基本思想就是将图像进行多分辨率分解, 分解成不同空间、不同频率的子图像 (分量), 然后对子图像进行系数编码。系数编码是小波变换用于压缩的核心, 压缩的实质是对系数的量化压缩。图像经过小波变换后被分解成4个频带分量:低频分量、水平分量、垂直分量和对角线分量, 水平分量含有较多的水平边缘信息, 垂直分量含有较多的垂直边缘信息, 对角线分量含有水平和垂直两个方向的边缘信息。低频分量作为母分量, 还可以重复上述过程, 进一步分解成4个子分量。图像经过小波变换后生成的系数图像的数据总量与原图像的数据量相等, 即小波变换本身并不具有压缩功能, 之所以将它用于图像压缩, 是因为生成的系数图像具有与原图像不同的特性, 表现在:
能量集中性。经过小波变换后, 图像的能量主要集中于低频部分, 而水平、垂直和对角线部分的能量则较少; 水平、垂直和对角线部分表征了原图像在水平、垂直和对角线部分的边缘信息, 具有明显的方向特性。
空间-频率的局部化。每一个小波系数仅仅包含原始输入图像的一个局部特性, 通过小波变换编码, 可以将输入图像分解为几个几乎不重叠的频带, 每个子带的频率含量各不相同, 表示原始图像在某一空间局部位置上一定频率范围的信息含量。
重要系数的群集性。重要系数是指幅度超过一定值的系数。Servetto等通过研究发现, 在同一个分量图像内, 重要系数的分布群集性通常比同等边缘概率下的二维Poisson分布还要高。重要系数在空间上对应着纹理和边缘, 而纹理和边缘通常具有群集性[12]。
各分量系数之间的相似性。Shapiro通过对各类图像的统计分析后发现, 母分量和子分量的幅度 (取平方以消除符号的影响) 相关度一般为0.20.6, 比较集中于0.35附近[13]。因此可以利用这个特性进行相关的量化处理 (如零树量化)。
分量系数幅度的衰减性。对于一幅自然图像, 可以将其假设为一个马尔可夫随机场, 根据统计信号处理的理论可以证明子分量的幅度一般比母分量小, 从母分量到子分量的系数幅度呈指数衰减。子分量对恢复图像的贡献度也相应减少, 量化后需要保留的值也相应减小。
1.3 气象卫星云图的小波特性分析与自然图像相比, 气象卫星云图有其自身特点。它与自然图像的差异主要表现在两个方面:原始图像的灰度分布和小波系数分布。为了更好地描述卫星云图的特殊性质, 本文选择接近于自然图像的Barbara图像与3个通道 (红外、水汽、可见光) 的卫星云图进行对比分析 (图略)。这些图像都经过了bior3.7双正交滤波器的五级分解。
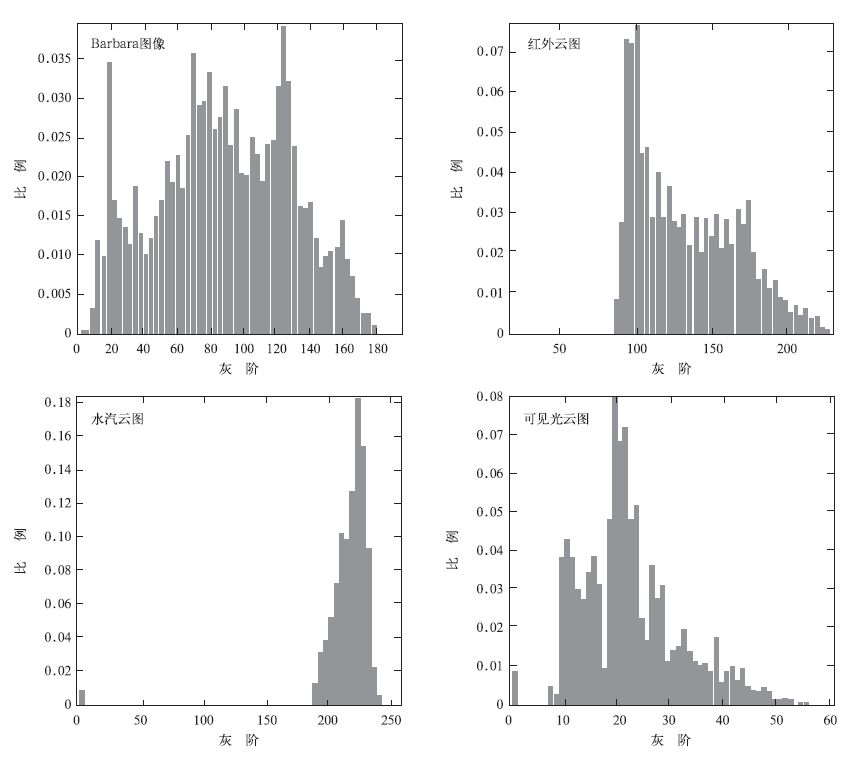
从原始图像的灰度分布上看: ①卫星云图的像素灰度范围较小, 相似区比例大。图 1给出了4幅图像的像素灰度统计直方图, Barbara图像的像素灰度分布为0~200的广大区域里, 跨度为200。与之相比, 卫星云图的灰度范围要小得多:红外云图的灰度范围为80~250, 跨度只有170, 水汽云图数值范围更窄, 只有不到70(180~245), 而可见光云图只有64个灰度等级, 跨度大约为45。卫星云图存在很大的相似区域, 在不同灰度级上像素分布非常有规律, 一般只有1个最大值, 且最大值与零点之间成缓慢的坡形过渡, 单调上升, 单调下降。而Barbara图像, 却存在多个大值点, 这是由于图片中存在多个独立物体所造成的。这种规律反映在小波系数分布上, 表现为低频分量比例更大, 高频分量比例较小。②卫星云图的像素间具有很强的相关性。这一点可以通过反映随机信号相关特性的自协方差矩阵的参数来说明, 式 (5) 和式 (6) 给出了自然图像和红外云图的自协方差矩阵, 所列自协方差矩阵中的元素已进行了归一化处理, 实际上是相关系数。从中可以看出, 如果将图像近似看成一阶马尔可夫过程, 则卫星云图的相关系数比自然图像的相关系数要大, 即卫星云图像素间的相关性 (或说像素间多余度) 要大于自然图像。
|
|
| 图 1. 原始图像灰度分布统计图 Fig 1. Gray scale statistics in original image | |

|
(5) |

|
(6) |
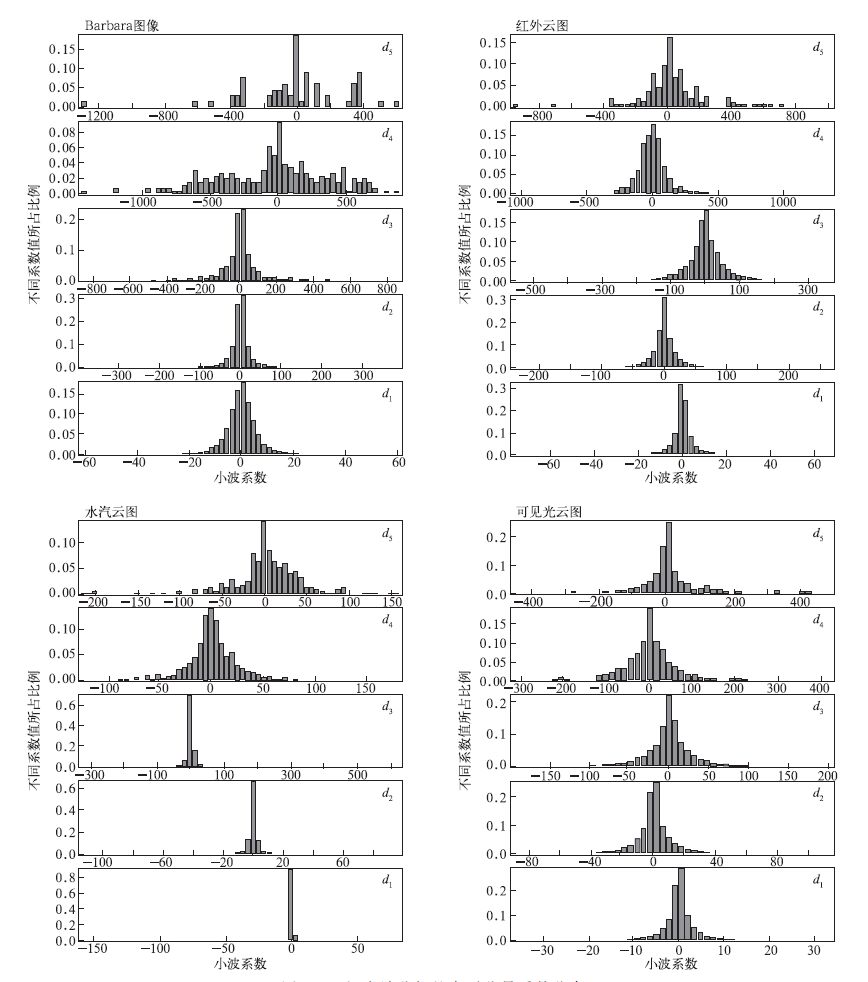
从小波系数分布上看: ①卫星云图的低频分量能量更为集中, 系数幅度更大。图 2是五级小波分解的低频分量系数分布图, 从图 2可以看出, Barbara图像的低频分量系数的数值范围较小, 且系数取值相对集中。卫星云图的低频分量系数的数值范围明显大于Barbara图像, 且取值分散。这说明卫星云图的能量更多地集中在低频部分②卫星云图的边缘分量系数幅度的衰减性更为明显。图 3给出了五级分解的水平分量系数 (包含水平边缘信息) 分布, 对于红外云图、水汽云图、可见光云图来说, 这种衰减一直维持到第5层, 还非常明显。而在Barbara图像上, 层次越高衰减越弱, 第4和第5层之间的系数值已相差不大。③卫星云图的边缘分量系数间存在明显的相关性和相似性。这种相关性不仅仅体现在同层小波系数之间, 不同层之间的相关性也高于自然图像。在卫星云图上 (图 3), 各层小波系数的分布规律与原始图像的灰度分布相似, 单调递增, 单调下降。而Barbara图像的系数分布就比较凌乱, 特别是在低分辨率层, 更为明显 (图 3)。边缘分量系数值更小, 近零点更多。图 3中, 红外云图和水汽云图的系数值都小于Barbara图像, 特别是水汽图像, 在第1层分解子图像中, 高频系数只有两个值:零或接近于零。

|
|
| 图 2. 五级小波分解的低频分量系数分布图 Fig 2. Low frequency component coefficient of five-step wavelet decomposed | |
|
|
| 图 3. 五级小波分解的水平分量系数分布 Fig 3. Horizontal component coefficient of five-step wavelet decomposed | |
以上几个特性, 对卫星云图的压缩非常重要, 如何更好地利用它们, 是实现卫星云图有效压缩的关键。而本文方案就是针对卫星云图的特性而设计。
2 基于零树小波编码的卫星云图压缩方案针对气象卫星云图特性, 本文设计完成了基于零树小波编码的气象卫星云图压缩方案。
2.1 卫星云图小波变换的实现 2.1.1 小波基 (小波滤波器组) 的选择正交性好且具有对称性的双正交滤波器是图像压缩的首选, 但常用的几种双正交滤波器组对卫星云图的压缩效果各不相同。
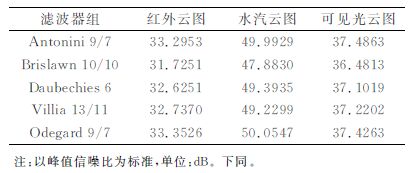
试验结果 (表 1) 表明:Antonini9/7滤波器组和Odegard9/7滤波器组的恢复图像质量远远好于其他滤波器组, 它们之间各有优势。考察两组滤波器在压缩比增大情况下的恢复图像质量。
|
|
表 1 各滤波器组恢复图像质量比较 Table 1 Comparison of the recovering image quality using different filters |
从表 2可以看出, 随着压缩比的增大, Odegard9/7滤波器组的优势也在增大, 在压缩比超过30:1后, 在所有通道上, Odegard9/7的图像质量都要好于Antonini9/7, 因此选择Odegard9/7滤波器组进行卫星云图的小波分解和重构。
|
|
表 2 Antoninni和Odegard恢复云图质量比较 Table 2 Comparison of Antoninni and Odegard recovering image |
2.1.2 卫星云图的分解与重构
卫星云图的小波分解与重构要在图像的行和列两个方向上进行, 每一级分解分为两个步骤:先将图像的每一行作为一个一维离散信号进行一级小波分解, 得到一个对行方向做完分解的系数矩阵; 然后将系数矩阵的每一列作为一个一维离散信号进行一级小波分解, 最后得到这一级分解以后的系数矩阵。在进行相应的重构时同样需要两个步骤, 先在列方向上进行一级小波重构; 再在行方向上进行一级小波重构。
2.1.3 分解级数的选择分解级数由两个因素决定: ①目标压缩比:在试验中希望达到的压缩比大约为60:1。②层次衰减性:卫星云图的高频系数幅值衰减直到五级分解时还很明显。
综合分析表明, 对卫星云图进行五级小波分解比较合适, 这样卫星云图的压缩比最大可达128:1(只保留最高级小波低频系数)。
2.2 小波系数的编码方案 2.2.1 改进的零树小波量化编码·零树编码算法
根据卫星云图小波分解系数相似性强、分量系数幅度层次衰减性明显的特点, 本文方案使用了最能体现小波系数相似性和层次性的零树编码算法[14-15]用以对小波系数的编码运算。主要步骤如下:
① 选择初始量化门限。
② 主扫描。使用当前量化门限, 按分解级由高到低比较各子带中尚未标明重要的, 且不属于当前门限下任何零树的小波系数, 产生以下4种码字并送至熵编码器。POS:系数幅值大于量化门限且符号为正; NEG:系数幅值大于量化门限且符号为负; ZTR:系数幅值小于量化门限且以该节点为根构成零树; IZ:系数幅值小于量化门限且以该节点为根不能构成零树。
③ 副扫描。对重要系数 (POS, NEG) 进行进一步的量化编码。
④ 将当前量化门限缩小一倍, 转至②。
⑤ 解码算法与编码完全对称 (解码值取每次量化区间的中值), 只需将输出改为输入。
·算法改进
为了提高编码效率, 根据卫星云图的特点, 本文对编码算法做了两点改进:最高层低频子带单独处理, 卫星云图的最高层低频子带集中了原始图像的绝大部分能量, 为了提高恢复图像的信噪比, 在量化过程中不对它进行零树编码, 而直接进行熵编码; 对红外和水汽云图最低层高频子带小波系数不编码, 对可见光云图编码方法不变, 红外和水汽云图的最低层高频子带系数值很小, 对重构图像的质量影响不大, 对它们进行多次扫描编码, 将造成时间和空间的过多的耗费。
2.2.2 熵编码方案对于零树编码输出的数据序列, 还要用熵编码对它进行进一步的压缩。算术编码是近似最优的熵编码算法, 因而成为各类小波编码器的首选。本文同样使用了算术编码作为作为熵编码方法。
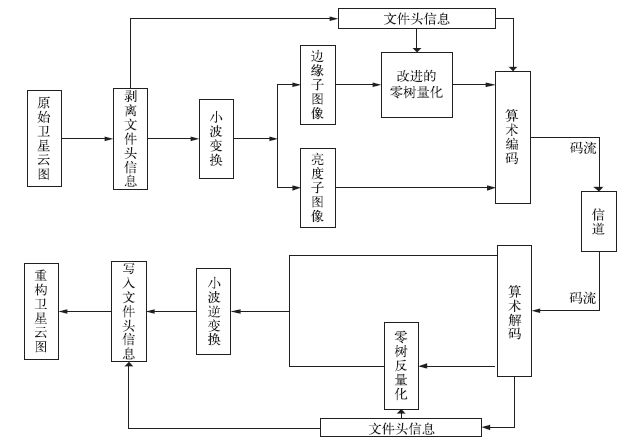
2.3 总体方案综上所述, 基于小波变换的气象卫星云图压缩方案的总体结构如图 4所示。
|
|
| 图 4. 基于小波变换的卫星云图压缩方案结构框图 Fig 4. Flow chart of meteorological satellite cloud image compression method based on wavelet transform | |
需要说明的是, 卫星云图文件由文件头信息和图像数据两部分构成, 在编码过程中, 本文根据卫星云图的存档格式进行了一致性转换:预先将文件头读出, 进行算术编码, 卫星图像的大小和类型也是从文件头信息中得到的。
3 结果分析 3.1 结果验证利用本文方案对红外、水汽、可见光等通道卫星云图进行了压缩实验, 恢复图像的质量采用峰值信噪比 (RPSN) 作为衡量标准 (式 (7)), 峰值信噪比越大, 图像失真越小。
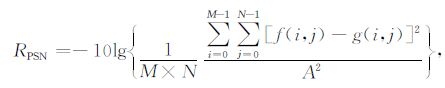
|
(7) |
式 (7) 中, f(i, j), g(i, j) 分别代表原图像和重建图像的像素值, A为最大像素值 (对于256色灰度图像, A取255), 图像尺寸为N×M, 单位dB。
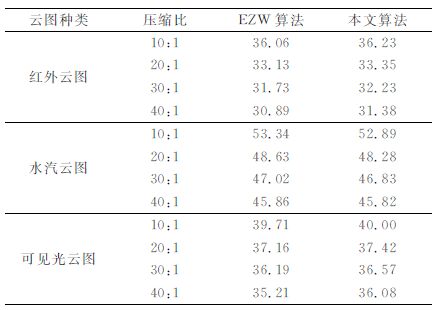
表 3列出了在不同压缩比 (10:1, 20:1, 30:1, 40:1) 的情况下, 本文算法和经典的嵌入式零树小波编码算法 (EZW算法) 对3类云图的压缩效果。其中, EZW算法仍使用通用的Antonini9/7滤波器组。试验结果显示, 在对红外云图和可见光云图的压缩上, 本文算法较EZW算法有一定改善。但在水汽云图的压缩上相差不大, 主要是由于在对水汽云图压缩时, 为了减少时间耗费, 将最高层系数抛弃的原因。不过, 随着压缩比的增大, 两者的压缩效果逐渐接近, 至40:1已相差无几。图 5给出了压缩比为30:1时3类图像的效果图, 其中水汽和可见光云图作了均衡化处理。与原始云图相比, 压缩后的图像在整体视觉效果上相差不大, 在云系细节上略有模糊, 但对于天气尺度云系分析影响不大。
|
|
表 3 EZW算法和本文算法压缩效果(峰值信噪比)比较 Table 3 Comparison between EZWmethod and the method in this paper |

|
|
| 图 5. 压缩比为30:1时恢复云图效果 Fig 5. Recovering cloud image at compression ratio of 30:1 | |
3.2 最大允许压缩比
一般认为, 由于人眼的视觉特性, 当峰值信噪比高于30后, 人眼很难再根据主观评价来分辨图像质量的好坏。也就是说, 如果恢复图像与原始图像的峰值信噪比大于30, 那么恢复图像质量可以满足要求。
但分析峰值信噪比计算公式 (式 (7)) 后发现:在图像的最大像素灰度值相似的情况下, 峰值信噪比的大小与图像灰度的相对取值范围有一定关系, 在同等质量条件下, 灰度范围越小, 峰值信噪比越大。由式 (7) 可见:峰值信噪比的大小由恢复图像和原始图像之间的灰度差异f(i, j)-g(i, j) 决定, 而灰度取值范围的缩小, 一般会导致绝对误差的缩小。而在峰值信噪比中, 灰度差异的参照值A取的是原始图像的最大像素灰度值 (一般取255), 并没有考虑像素的取值范围 (最大像素值与最小像素值之间的差异)。这种情况下, 图像的最大像素灰度值相似时, 可能会出现灰度范围越小, 峰值信噪比越大的情况。试验结果显示 (图略), 这个问题确实存在, 当峰值信噪比相同时, 水汽云图的图像质量要明显差于红外云图。其原因在于, 红外云图灰度值跨度为170, 而水汽云图灰度值跨度为70。因此, 在衡量最大允许压缩比时必须考虑灰度的取值范围。但由于小波压缩算法比较复杂, 还无法给出一个定量的衡量标准。只能以定性的方式, 辅以试验来寻找合适的压缩比。红外云图灰度值跨度大约为170, 最大值为240左右, 则其允许失真的峰值信噪比应稍大于30;水汽云图灰度值跨度大约为70, 最大值为240左右, 允许失真的峰值信噪比应远大于30;可见光云图灰度值跨度大约为45, 最大值为53左右, 允许失真的峰值信噪比应大于红外云图, 但小于水汽云图。
按照这个原则, 经过试验得出了3通道云图的近似最大压缩比:红外云图大约为40:1、水汽云图大约为60:1, 可见光云图大约为35:1。
4 小结本文在分析总结气象卫星云图特点的基础上, 设计并实现了基于小波变换的气象卫星云图的压缩方案。方案利用对卫星云图压缩效果最好的具有双正交性的Odegard9/7滤波器组对卫星云图进行了五级小波分解和重构。并根据卫星云图小波分解系数相似性强、分量系数幅度层次衰减性明显的特点, 使用改进后的零树编码算法对小波系数进行了编码运算。最后, 采用高效的自适应算术编码对输出数据流进行了进一步的压缩。
根据对式 (7) 的分析和试验对比, 本文提出了一个假定:在图像的最大像素灰度值相似的情况下, 峰值信噪比的大小与图像灰度的相对取值范围有一定关系, 在同等质量条件下, 灰度范围越小, 峰值信噪比越大。
这个假定已通过对卫星云图的压缩试验得到了部分验证, 但是否具有一般性还需进一步探讨。根据本文假定, 在失真允许情况下, 对红外云图的近似最大压缩比达40:1(峰值信噪比为31.38), 水汽云图达60:1(峰值信噪比为44.87)、可见光云图达35:1(峰值信噪比为36.89)。
卫星云图的有效压缩是提高卫星资料传输存储效率的重要前提, 本文算法提供了一种较为有效的压缩方案, 但主要应用于数据量较小的分区图像 (数据量小于3 MB), 大数据量的全分辨率圆盘图和极轨图像数据的压缩需要更高的压缩效率, 要实现大容量卫星数据高效压缩, 还需做大量工作。
| [1] | 方宗义, 覃丹宇. 暴雨云团的卫星监测和研究进. 应用气象学报, 2006, 17, (5): 583–593. |
| [2] | 谷德军, 王东晓, 纪忠萍, 郑彬. 墨西哥帽小波变换的影响域和计算方案新探讨. 应用气象学报, 2009, 20, (1): 62–69. |
| [3] | 孙卫国, 程炳岩. 交叉小波变换在区域气候分析中的应用. 应用气象学报, 2008, 19, (4): 479–487. |
| [4] | Burrus C S, Gopinath R A, Guo H T.Introduction to Wavelets and Wavelet Transforms.New Jersey:Prentice Hall Press, 1998. |
| [5] | Mallat S, Multifrequency channel decomposition of images and wavelet models, IEEE Transactions on Acoustics.. Speech and Signal Processing, 1989, 37, (12): 2091–2110. DOI:10.1109/29.45554 |
| [6] | Taubman D, Zakhor A, Mulirate 3-D subband coding of video. IEEE Transactions on Signal Processing, 1994, 4, (9): 572–588. |
| [7] | Xiong Z, Ramchandran K, Orchard M T, A comparative study of DCT-and wavelet-based image coding. IEEE Transactions on Circuits and Systems for Video Technology, 1999, 9, (5): 692–695. DOI:10.1109/76.780358 |
| [8] | Daubechies I, The wavelet transform:Time-frequency localization and signal analysis. IEEE Transactions on Information theory, 1990, 36, (5): 961–1005. DOI:10.1109/18.57199 |
| [9] | Chui C K, An Introduction to Wavelet,. London, UK: Academic Press, 1992. |
| [10] | 程正兴. 小波分析算法与应用. 西安: 西安交通大学出版社, 1998. |
| [11] | 陈武凡. 小波分析及其在图像处理中的应用. 北京: 科学出版社, 2002. |
| [12] | Servetto S D, Ramchandran K, Orchard M T, Image coding based on a morphological representation of wavelet data wavelet. IEEE Transactions on Image Processing, 1999, 8, (9): 1161–1174. DOI:10.1109/83.784429 |
| [13] | 吴建华, 占传杰, 黎鹰, 王顺长. GMS卫星红外云图数据压缩. 中国图象图形学报, 1999, 4, (1): 56–60. |
| [14] | Shapiro J, Embeded image coding using zerotrees of wavelet coefficients. IEEE Transactions on Signal Processing, 1993, 41, (12): 3445–3462. DOI:10.1109/78.258085 |
| [15] | Lewis A S, Knowles G, Image compression using 2-D wavelet transform. IEEE Transactions on Signal Processing, 1992, 1, (2): 244–250. |
 2010, 21 (4): 423-432
2010, 21 (4): 423-432