在大气变化过程中,降水是对人类活动影响最大的气象要素之一。然而降水普遍具有空间上和时间上的不均匀性和不连续性,当降水出现过多、过少或分布不均等异常时将导致洪涝干旱等气象灾害。因此,准确掌握降水量大小和分布对于防灾减灾起着关键性作用。
目前,通过雨量计观测是最直接、有效、也是最为常用的获得降水信息的方法,但雨量计观测在空间上分布不均匀,获得的也只是站点上的降水量,在空间上分布不连续,要得到规范网格上降水量 (或面降水量) 需要经过一些数学方法处理。为此许多科学家做了大量的研究和实践工作,发展出不少插值方法,常用的有:Cressman[1],Barnes[2],Gandin[3],Shepard[4]和Hulme[5]等,其基本思路是:利用站点上观测得到的降水量,通过建立未知网格点与已知站点之间的数学关系估测网格点上的降水量。国内日降水量插值研究较少[6-12];Bussieres等[13]和Chen等[14]分别对这些插值方法在日降水量和月降水量分析中的表现进行了对比检验,认为Gandin最优插值法有比较好的准确性和稳定性,效果最佳。但在小时时间尺度上运用何种数学关系的插值方法以及如何设置有关参数才更为有效,需要做进一步验证。
1 资料和方法本研究所用雨量计资料为广东、广西2007年5月20日—8月30日自动站逐小时降水量观测资料,在4.14×105km2面积上雨量计达到1766个。
所使用的客观插值方法为Shepard插值方法[4]和最优插值 (简称OI) 方法[3-5, 13-14]。Shepard方法是一种典型的考虑距离效应的插值方法,OI方法是考虑了格点与站点资料之间关系的一种插值方法,最早由Gardin提出,在应用中有比较好的效果。
为了检验插值方法的实际效果,本文采用交叉检验方法[15]。具体方案为:首先随机抽取10%的站点资料,用余下的90%站点值进行插值,比较所得降水量场上未被用来插值的站点上降水量插值结果与站点实际降水量的误差,然后在余下的90%站点里抽取10%站点,再用总场余下的90%站点值进行插值,比较被抽取站点上的误差,如此重复10次,保证每个站点都被选取。由此得到的降水量插值场和原站点降水量场进行对比,进行相关分析,并考查平均偏差、相对误差和均方根误差。
关于地形效应对降水影响的考虑,参考国外成果[16-17],本文定义考虑了地形影响效应的日降水量气候分析场。首先收集试验区域雨量站最近30年的日降水量资料,并计算出各站30年日气候平均值。然后通过傅立叶变换消除日气候平均序列的高频噪声,并用PRISM (Parameter-elevation Regres-sionson Independent Slope Model) 月气候分析场来校正上述计算出的日降水量气候场,使得校正后的日降水量气候场累积值与PRISM接近而时间变化又与校正前相似。PRISM是美国州立大学空间气候研究中心所开发的一种基于地理空间特征和回归统计方法生成气候图的模型[6-7, 18-19],它较好地体现了气象要素与地形要素之间的相关关系并辅助以专家知识系统以达到对具有强时空变异性的气象参数空间制图的目的[19]。其原理基于以下几个方面[7, 19]: ①高度对气象要素的影响。气象要素随着高度的变化而发生显著变化,一般情况,温度随着高度的增加而降低,而降水量则随着高度的增加而增加,至某一高度达到最大值后才转而逐渐向上递减[20-22],山区降水量随高度分布的规律很复杂,一般在不同地区有较大差异。②风阻挡等因素的影响。通过将某一复杂的山地景观区分为不同的“地形趋势面"[7, 18-19]来综合考虑地形要素对降水空间格局的影响。③垂直分层的影响。考虑在大气逆温和低湿条件下,气象要素并不是随高度变化表现出一种单调的变化,在垂直方向上将研究区分为若干层,在各层内讨论气象要素的变化梯度[19]。④距海岸远近的影响。大型水体对临近地区气象要素变化的影响强烈,濒海地区必须考虑海洋对气候的影响,以离海岸的远近来衡量其影响的强弱[18-19]。在PRISM中,认为高度是影响气象要素空间分布最重要的因素,并根据观测站点的高度值与气象要素的观测值,采取线性回归的方法,建立高度与气象要素之间的回归方程[6]。这里使用的PRISM月降水量气候场是由Daly等[23-24]用半客观半主观方法制作的考虑了地形效果的气候场。在制作中国地区的PRISM时,Daly等使用了超过2600个台站气候观测资料,是国际上被公认为最好的考虑了地形影响的降水量气候场。
在得到经过地形校正后的日降水量气候分析场后,逐时降水量分析场的计算将分两步实施。首先计算各测站上实测小时降水量与相应日期考虑了地形效应的日降水量气候值的比率 (当分母为零时,加上一个小量0.1),并用Shepard和OI方法将该比率内插到网格点上得到比率的分析场;然后将比率分析值与日降水量气候分析值相乘得到考虑地形影响效应的小时降水量分析场。这一方法可称之为比率法。由于日降水量气候分析值考虑了地形影响的气候效应,因此小时降水量从气候平均上也考虑了地形的影响效应。
2 Shepard和OI方法对雨量计资料的分析对比从2007年5月20日—8月30日雨量计降水量平均值分布图上 (图略) 可以看到,珠江三角洲地区雨量计站点比较密集,广东其他地区雨量计站点分布比较均匀,大的降水中心主要集中在沿海地区。相比之下,广西的西北部地区相对比较稀疏,而大的降水中心主要分布在西北部地区。总的来说,雨量计在空间上分布不均匀。
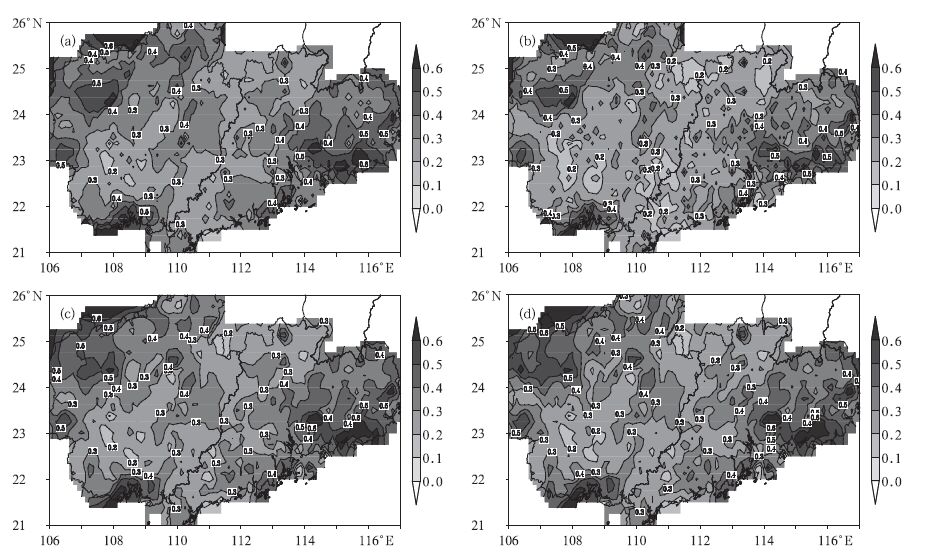
为了得到规范网格上降水量,采用Shepard和OI两种方法分别将雨量计逐时降水量插值到21°~26°N,106°~117°E范围0.125°×0.125°网格点上,从而比较两种方法的优异性。图 1a和图 1c是将降水量直接插值结果,图 1b和图 1d是考虑了地形影响效应的降水量气候分析场,用比率法插值的结果。由图 1可见,无论是用Shepard还是用OI方法进行直接插值,降水空间分布大体一致,大雨中心没有发生漂移,体现出广西西北部和广东东部沿海地区降水量较大的分布特征 (图 1a和图 1c),与实况样本分布也较吻合。相比之下,加入地形影响效应的降水量气候分析场得到的降水量插值分布场 (图 1b和图 1d) 更好地刻画了降水量大值中心分布,同时对逐小时0.4 mm以下降水量分布也有很好体现,尤其是OI方法,较真实地反映了雨量计站点降水量分布特征。
|
|
| 图 1. 2007年5月20日-8月30日21°~26°N, 106°~117°E区域雨量计观测值时间平均空间分布(单位:mm)(a)OI方法插值格点平均,(b)比率OI方法插值格点平均,(c)Shepard方法插值格点平均,(d)比率Shepard方法插值格点平均 Fig 1. Distribution of temporal mean gauge observations in the region of 21°-26°N, 106°-117°E from 20 May 2007 to 30 Aug 2007 by interpolation at grids (unit:mm)(a) OI, (b) OIratio, (c) Shepard, (d) Shepard ratio | |
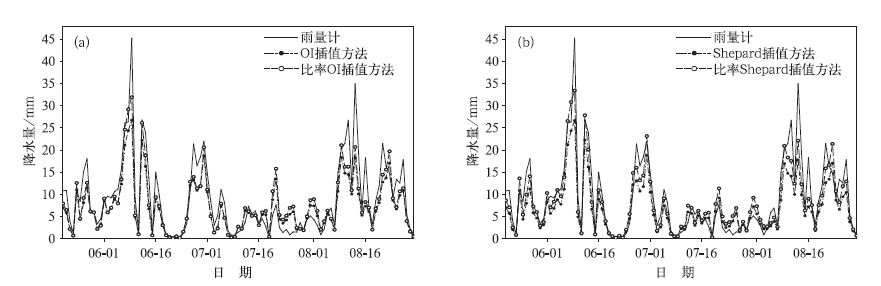
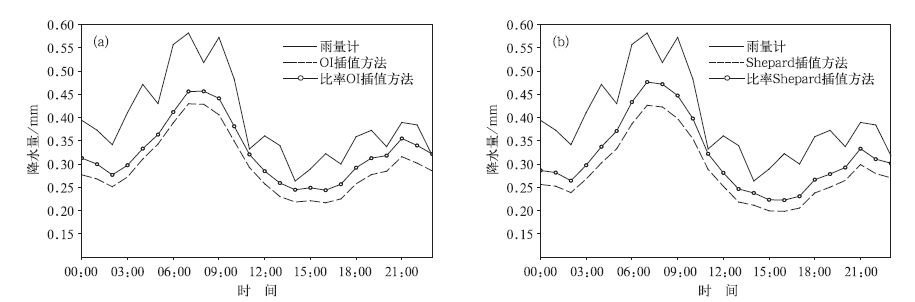
从客观分析得到的降水量场估算出站点上的降水量,并计算出分析区域内所有站点的日平均降水量,比较客观分析方法得到的日平均降水量与雨量计日平均降水量的时间变化,如图 2所示。从区域雨量计日平均降水量变化来看,2007年5月20日—8月30日,两广地区降水比较丰富,出现了多次明显的强降水过程,如6月、7月上旬和8月上旬。用OI和Shepard插值方法计算得到与之相一致的变化特征。从两者的相关系数来看,用比率OI插值方法得到的日平均降水量和雨量计站点降水量的相关最高,相关系数为0.93;其次为用比率Shepard插值方法,相关系数为0.92;再次为OI插值方法,相关系数为0.91;而用Shepard插值方法,相关系数为0.90。另外,从研究时段平均日变化来看 (图 3),雨量计站点逐时降水量具有明显的双峰型日变化特征,最高出现在07:00—08:00(世界时,下同),次高值出现在21:00,最低值出现在16:00和02:00,日变化特征很显著。由OI和Shepard插值方法得到的降水强度均偏低,这主要是内插值与站点观测值的空间代表性差异引起的,内插值的定义偏重代表网格内空间的平均,而站点观测值是空间上的测量值。不过反映的日变化特征仍很显著,与观测值的双峰型变化相一致。从图 3可以明显看出,考虑地形影响效应进行插值得到的结果与观测值更为接近。
|
|
| 图 2. 2007年5月20日-8月30日21°~26°N, 106°~117°E区域平均的逐日降水量变化曲线(a)OI与比率OI插值方法,(b)Shepard与比率Shepard插值方法 Fig 2. Variationof regional 24-hour mean precipitation in the region of 21°-26°N, 106°-117°E from 20 May 2007 to 30 August 2007(a) OI and OI ratio, (b) Shepard and Shepard ratio | |
|
|
| 图 3. 2007年5月20日-8月30日21°~26°N, 106°~117°E区域平均的降水日变化(a)OI和比率OI插值方法,(b)Shepard和比率Shepard插值方法 Fig 3. Diurnal variation of regional mean precipitation in the region of 21°-26°N, 106°-117°E from 20 May 2007 to 30 August 2007(a) OI and OI ratio, (b) Shepard and Shepard ratio | |
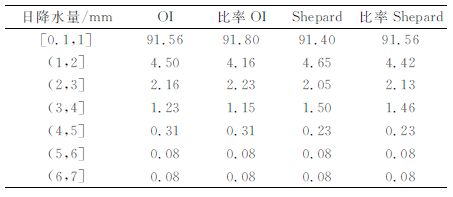
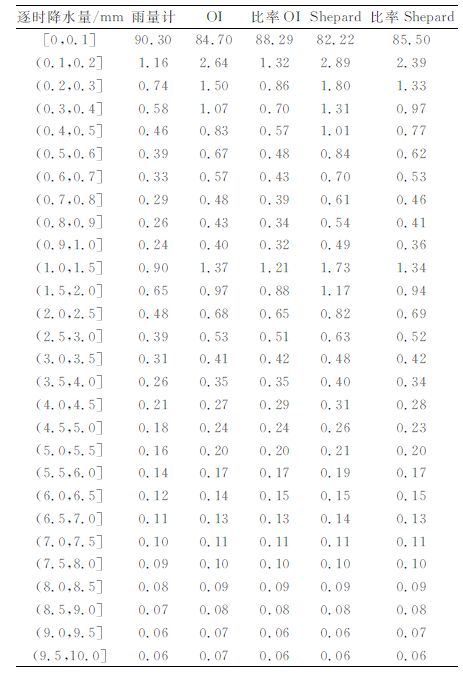
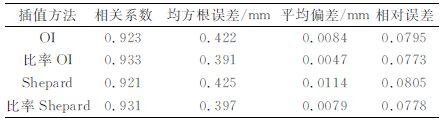
为了进一步比较用OI、比率OI和Shepard、比率Shepard4种插值方法得到的格点分析资料的可靠性及差异性,将插值得到的格点资料再分别回插到站点,并计算与原雨量计站点资料的相关系数、均方根误差、平均偏差和相对误差。从相关系数分布来看 (图略),无论是逐日变化还是日变化,在雨量计分布较密集的大部分地区,由4种方法得到的相关系数都大于0.4,相关显著 (达到0.01显著性水平),部分地区相关系数还高于0.8(如雨量计分布密集的广东)。相应地,均方根误差、平均偏差和相对误差也较小 (图略),说明由4种插值方法得到的格点资料与雨量计资料之间存在很好的对应关系。但是,在雨量计分布相对稀疏的广西西北地区,相关系数较低,均方根误差、平均偏差和相对误差均较大,因此使用插值得到的格点资料时应注意这一点。由于OI、比率OI和Shepard、比率Shepard4种插值方法间的细小差异性在空间分布图上不易体现,因此不便于比较。加之考虑到篇幅关系,在此仅以均方根误差百分比 (即用OI、比率OI和Shepard、比率Shepard方法得到的逐日格点降水值分别插回站点上,再与雨量计逐日降水值计算均方根误差在各个等级所占的百分比) 为例,给出其逐日变化情况 (表 1)。由表 1可以看出,用比率OI插值方法得到的均方根误差在1 mm以下所占的百分比最大,且该均方根误差所占等级百分比随等级增大而递减最明显,由此说明,加入地形影响效应的降水量气候分析场进行最优插值得到的结果与观测值更为接近。此外,从各逐时降水量等级出现概率来看,最大概率出现在1mm/h以下,达到90.3%,依次迅速递减。用OI和Shepard方法得到的降水概率密度分布也呈现相应变化特征,但1 mm以下逐小时降水量趋势估计偏低,1 mm以上逐小时降水量趋势估计偏高。相比之下,用比率法进行插值得到的概率分布密度要比直接进行插值得到的概率分布更能接近观测值。同时,表 2也表明用OI方法要比Shepard方法能更好地反映观测值的变化。此外,从雨量计降水日变化也能得出同样的结论。
|
|
表 1 OI、比率OI和Shepard、比率Shepard方法得到的均方根误差百分比(单位:%) Table 1 Contrast of root-mean-square error percentage between the gauge and grid interpolation by OI, OI ratio, Shepard and Shepard ratio (unit:%) |
|
|
表 2 逐时变化降水量概率密度分布(单位:%) Table 2 Hourly probability density distribution (unit : %) |
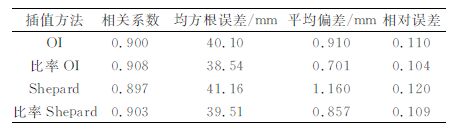
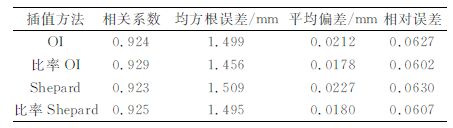
交叉检验方法是进一步验证以上方法有效性的一种重要途径,在此对上述4种客观分析方法用交叉检验方法进行检验,比较各种方案的误差和优劣。误差分析结果见表 3~表 5。可以看出,无论是月变化、逐日变化还是日变化,相关系数、均方根误差、平均误差以及相对误差均表明用Shepard方法直接插值的误差最大,和雨量计站点观测值的相关最小,其估值精度低于其他方法。而考虑地形影响效应,用比率OI方法插值得到的误差最小,能有效提高相关性,更好地估测出降水量的真实值。
|
|
表 3 降水量月变化OI和Shepard方法的交叉检验 Table 3 Cross-validation of monthly rain variation by OI as compared with Shepard |
|
|
表 4 降水量逐日变化OI和Shepard方法的交叉检验 Table 4 Cross-validation of daily rain variation by OI as compared with Shepard |
|
|
表 5 降水量日变化OI和Shepard方法的交叉检验 Table 5 Cross-validation of diurnal rain variation by OI as compared with Shepard |
3 小结
本文引入考虑地形影响效应的日降水量气候分析场,分别运用OI和Shepard两种插值方法对广东和广西2007年5月20日—8月30日汛期小时雨量计降水量进行插值,得到0.125°×0.125°分辨率的规范化网格分布,结果表明:
1) 无论是直接插值还是用降水比率 (引入考虑地形影响效应的日降水量气候分析场) 插值,降水量空间分布大体一致,大雨中心没有发生漂移。降水比率插值方法更好地刻画了降水大值中心分布,同时对0.4 mm/h以下降水量的分布也有很好体现,尤其是比率OI插值方法。
2) OI和Shepard两种插值方法均能很好地体现广东和广西雨量计站点降水量的季内变化和日变化特征,但插值结果较实况偏低,主要由内插值与站点观测值的空间代表性差异引起。降水比率OI插值方法得到的结果与实况更为接近。
3) 用降水比率插值方法得到的降水空间估值精度高于直接插值方法。
4) 交叉检验表明,考虑地形影响效应的降水比率OI方法为最优方法,能有效提高相关性并减少均方根误差和系统误差。
| [1] | Cressman G P, An operational objective an alysis system. Mon Wea Rev, 1959, 87: 367–374. DOI:10.1175/1520-0493(1959)087<0367:AOOAS>2.0.CO;2 |
| [2] | Barnes S L, A technique for maximizing details in numerical weather map analysis. J Appl Meteor, 1964, 3: 396–409. DOI:10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2 |
| [3] | Gandin L S, Objective Analysis of Meteorological Fields. Is-rael Program for Scientific Translations, 1965: 1–242. |
| [4] | Shepard D, A Two Dimensional Interpolation Function for Regu-larly Spaced Data.Proc 23rd National Conf of the Association for Computing Machinery. Princeton, NJ, ACM, 1968: 517–524. |
| [5] | Hulme M, A 1951-80 global land precipitation climatology for the evaluatuin of general circulation models. Climate Dyn, 1992, 7: 57–72. |
| [6] | 朱求安, 张万昌, 赵登忠. 基于PRISIM和泰森多边形的地形要素日降水量空间插值研究. 地理科学, 2005, 25, (2): 233–238. |
| [7] | 朱华忠, 罗天祥, DalyC. 中国高分辨率温度和降水模拟数据的验证. 地理研究, 2003, 22, (3): 349–359. |
| [8] | 蔡福, 于慧波, 矫玲玲, 等. 降水要素空间插值精度的比较---以东北地区为例. 资源科学, 2006, 28, (6): 73–79. |
| [9] | 刘登伟, 封志明, 杨艳昭. 海河流域降水空间插值方法的选取. 地球信息科学, 2006, 8, (4): 75–79. |
| [10] | 高歌, 龚乐冰, 赵珊珊, 等. 日降水量空间插值方法研究. 应用气象学报, 2007, 18, (5): 732–736. |
| [11] | 庄立伟, 王石立. 东北地区逐日气象要素的空间插值方法应用研究. 应用气象学报, 2003, 14, (5): 605–615. |
| [12] | 杨彬云, 吴荣军, 杨保东, 等. 近40年河北省地表干燥度的时空变化. 应用气象学报, 2009, 20, (6): 745–752. |
| [13] | Bussieres N, Hogg W, The objective analysis of daily rainfall by distance weighting schemes on a mesoscale grid. Atmos O-cean, 1989, 27: 521–541. DOI:10.1080/07055900.1989.9649350 |
| [14] | Chen M, Xie P, Janowiak J E, et al. Global land precipitati-on:A 50-year monthly analysis based on gauge observations. J Hydrometeor, 2002, 3: 249–266. DOI:10.1175/1525-7541(2002)003<0249:GLPAYM>2.0.CO;2 |
| [15] | 李海滨, 林忠辉, 刘苏峡. Kriging方法在区域土壤水分估值中的应用. 地理研究, 2001, 20, (4): 446–452. |
| [16] | Schaake J, Henkel A, Cong S.Application of PRISM Clima-tologies for Hydrologic Modeling and Forecasting in the Western US.18th AMS Conf on Hydrology, Seattle, WA, 2004. |
| [17] | Xie P P, Arkin P A, Analyses of global monthly precipitation using gauge observations, satellite estimates, and numericalmodel predictions. J Climate, 1996, 9: 840–858. DOI:10.1175/1520-0442(1996)009<0840:AOGMPU>2.0.CO;2 |
| [18] | Daly C, Neilson R P, Phillips D L, Astatistical-topographic model for mapping climatological precipitation over mountani-ous terrain. J Appl Meteor, 1994, 33: 140–158. DOI:10.1175/1520-0450(1994)033<0140:ASTMFM>2.0.CO;2 |
| [19] | Daly C, Wayne P G, George H T, et al. A knowledgy-based approach to the statistical of climate. Climate Research, 2002, 22: 99–113. DOI:10.3354/cr022099 |
| [20] | 汤懋苍. 祁连山区降水的地理分布特征. 地理学报, 1985, 40, (4): 323–332. |
| [21] | 张学成, 杨针娘. 祁连山冰沟流域水量平衡初析. 冰川冻土, 1991, 13, (1): 35–42. |
| [22] | 王根绪, 程国栋. 内陆河流域生态环境的空间分异特征. 地理科学, 1998, 18, (4): 355–361. |
| [23] | Daly C, Gibson W P, Doggett M, et al.Up-to-date Monthly Climate Maps for the Conterminous United States.Proc, 14th AMS Conf on Applied Climatology, 84th AMS Annual Meeting Combined Preprints, Amer Meteorological Soc, Se-attle, WA, 2004. |
| [24] | Daly C, Gibson W P, Doggett M, et al.AProbabilistic-spa-tial Approach to the Quality Control of Climate Observa-tions.Proc, 14th AMS Conf on Applied Climatology, 84th AMSAnnual Meeting Combined Preprints, Amer Meteoro-logical Soc, 2004. |
 2010, 21 (4): 416-422
2010, 21 (4): 416-422