2. 南京信息工程大学信息与控制学院, 南京 210044;
3. 广西壮族自治区气候中心, 南宁 530022
2. School of Information and Control Technologies, Nanjing University of formation Science & Technology, Nanjing 210044;
3. Climate Center of Guangxi Zhuang Autonomous Region, Nanning 530022
气候系统是一种耗散的高阶非线性系统, 在气候预测中, 对于处理非线性时序问题有独特优越性的人工神经网络等技术已得到了一定应用。如张迎春等[1]采用基于时间序列的BP (Back Propagation) 神经网络对克拉玛依沙漠进行气温预测分析; 金龙等[2]采用了基于遗传算法的BP神经网络进行短期气候预测建模研究; 陈永义等[3-4]首次将支持向量机方法引入到气象预报试验中, 冯汉中等[5]、燕东渭等[6]、刘科峰等[7]在此基础上进行了更深入的探索, 取得了较好的预报效果。
同时, 气候时间序列也具有典型的非平稳特征[8], 可以借助信号处理方法进行平稳化处理, 以获得更好的预测效果。Huang等[9]于1998年提出了一种新的信号处理方法———经验模态分解 (Empiri-cal Mode Decomposition, EMD)。它将非平稳信号按不同尺度的波动或趋势分解成若干个本征模态函数 (Intrinsic Mode Function, IMF) 分量及一个趋势分量的线性和。不同的IMF分量是平稳信号, 具有非线性特征, 也具有时间上的局域化特征。经验模式分解结果完全由信号本身决定, 是一种自适应信号分解方法, 其滤波特性与小波分解非常相似。目前, EMD算法已在多时间尺度分析[10]、时间序列预测[11]、故障诊断[12]等多个方面获得了较好的应用效果。
本文采用广西夏季的逐年降水距平百分率资料, 将EMD算法与支持向量机 (Support Vector Machine, SVM) 时间序列预测算法相结合, 进行短期气候预测。经验证, 相对于不使用EMD的BP神经网络和SVM进行的预测, 本文中提出的方案能够取得更好的效果。
1 经验模态分解 1.1 经验模态分解基本步骤EMD算法将时间信号X(t) 分解成一系列的IMF分量, 每个IMF具有如下两个特征:从全局特性上看, 极值点数必须和过零点数一致或者至多相差1个; 在某一个局部点, 极大值包络和极小值包络在该点的值的算术平均值是零。详细分解步骤如下[9]:
(1) 对于输入序列X(t) 进行标准化处理, 得到序列S(t)。判断S(t) 的极值数是否大于2:是, 则继续执行; 否, 则跳转到步骤 (4)。
(2) 定义H(t)=S(t), 在H(t) 中进行提取IMF分量的循环操作, 包括:
①提取H(t) 序列中的极大值和极小值。通过插值算法将极大值和极小值插值到整个时间段上, 得到max (t) 和min (t), 并计算算术平均值m(t)。
②令H(t)=H(t)-m(t)。此时的H(t) 有可能为IMF分量, 通过一系列的约束条件来加以判断:
(Ⅰ) 满足上述的IMF分量的两个特征。
(Ⅱ) 为了防止过分迭代, 设置H(t) 的最大迭代次数为200。
(Ⅲ) 通过限制两个连续的处理结果之间的标准差D的大小进行约束, 如式 (1) 所示。一般D的取值在0.2~0.3之间:
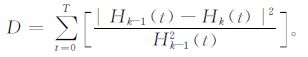
|
(1) |
③若以上条件都满足, FIM(t)=H(t), 跳出循环; 否则转到①继续迭代。
(3) 成功提取一个IMF分量, 并令S(t)=S(t)-FIM(t), 跳转到步骤 (1)。
(4) 此时所有的IMF分量都被提取出, 剩余的S(t) 则表现为一个单调或近似单调的趋势项, 称为趋势分量Rn(t)。时间序列实现分解:
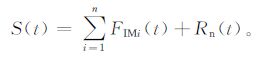
|
(2) |
根据上述的算法原理可以看出, 经验模态分解过程中最关键的一步是通过信号的极值点拟合信号包络线, 而目前尚未从理论上严格确定采用何种包络线算法[13]。文中采用的是应用最广泛的三次样条插值函数法。三次样条函数需要信号两端数据的一阶或二阶导数作为其边界已知条件, 而由EMD算法的原理可知, 无法直接获得两端点对应的极值, 因此许多学者运用多种方法来拟合信号的端点极值, 主要有黄大吉等[14]提出的极值延拓法, Zhao等[15]提出的镜像延拓法, 朱金龙等[16]提出的正交多项式拟合法以及邓拥军等[17]提出的线性神经网络法。
针对本文在短期气候预测方向的应用, 神经网络延拓方法的速度过慢[18], 无法适用实际需求; 镜像延拓法可能需截去一部分数据以获得极值点位置, 对于本文的短时间序列也不适合。因此将原序列首先进行标准化处理后, 分别采用极值延拓法和正交多项式拟合两种方法进行端点延拓, 对比结果如图 1所示。

|
|
| 图 1. 极值延拓法 (a) 与正交多项式拟合法 (b) 的EMD处理结果 Fig 1. Results of EMD based on extrema extending algorithm (a) and orthogonal polynomial fitting algorithm (b) | |
其中, 图 1a采用的是极值延拓法, 图 1b采用的是正交多项式拟合法。从分解结果可以看出, 运用两种端点延拓方法所得分量个数是一致的, 均为4个IMF分量和一个趋势分量; 且FIM1(t) 的振幅最大, 波长最短, 之后依次减小, 符合EMD算法的原理。不过, 从图 1b中可以看出, FIM2(t) 分量的左端点处出现了明显的振幅过大, 即所谓的端点飞翼现象, 这直接影响到了FIM3(t) 的值。从算法原理上看, 正交多项式拟合法[16]是通过构造一个正交多项式函数对离端点最近的有限个已知极值点 (由于序列较短, 这里取3个) 进行数据拟合, 拟合的标准是最小二乘法。不足之处在于, 为了获得最佳的拟合效果, 多项式阶数较高, 导致在端点处 (特别是时间序列的起始零点) 振幅过大, 曲线严重失真, 如图 1b中的FIM2(t) 分量; 当多项式取一阶或二阶时, 曲线会更加平滑, 但可能不满足最小二乘的条件; 并且所取的拟合极值点个数也是人为确定, 没有严格限制。而极值延拓法是根据序列内极值点出现的位置以及与端点的关系, 向两侧进行对称的延拓。对延长的新序列使用三次样条插值后, 再截去人为延拓的部分。由于使用了已知的极值点作为延拓的端点, 从而有效地避免了端点的飞翼现象。因此, 实际中采用极值延拓法作为端点极值拟合方法。
2 SVM时间序列预测 2.1 时间序列构造设有时间序列{x(1), x(2), …, x(N)}, 根据时间序列的历史数据{x(t), x(t-1), …, x(t-m+1)}预测未来t+k时刻的值x(t+k), 使其满足

|
(3) |
称为时间序列的预测。而将SVM应用于时间序列预测, 是指用SVM拟合函数F, 将时间序列建模与预测问题转换成SVM的回归估计。其中, 当k=1时, 称为单步预测; 当k>1时, 称为多步预测。这种多步预测为迭代式, 即每次进行的仍为单步预测, 将得到的结果作为下一步预测的输入, 来计算接下来的预测值。参数m称为嵌入维数, 一般根据实际情况选取。
2.2 基于SVM的时间序列预测SVM是一种基于统计学习理论的机器学习方法, 遵循结构风险最小化准则。相对于其他机器学习算法, 具有结构简单, 全局最优, 泛化能力好的特点, 更适合解决小样本情况下的学习问题[19]。本文采用由Suykens等[20]提出的一种SVM改进算法———最小二乘支持向量机 (least squares support vector machines, LS-SVM) 算法, 与传统SVM算法相比, 可降低计算复杂度, 提升求解速度。用于时间序列预测的LS-SVM回归算法关键步骤描述如下:
给定一个含N个样本的训练集{xk, yk}k=1N, 其中, xk为n维输入向量, yk是一维输出标量。首先通过非线性映射函数φ(xk) 将输入向量映射到特征空间, 并表示成最优化问题:
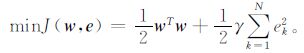
|
(4) |
约束条件为:
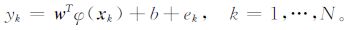
|
(5) |
式 (4)~(5) 中, w为权重向量, ek为松弛变量, b为偏置, γ是正则化参数, 它能够在训练误差和模型复杂度之间取一个折衷以便使所求的函数具有较好的泛化能力。接下来引入拉格朗日函数求解该优化问题:

|
(6) |
式 (6) 中, αk为拉格朗日乘子。根据KKT优化条件, 并定义核函数K(x, xk)=φT(x)φ(xk), 通过求解线性方程组得到回归的决策函数为:
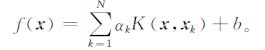
|
(7) |
这里, 核函数选取常用的径向基核函数:

|
(8) |
其中, σ为径向基核宽度, 和正则化参数γ一样均为待定参数。本文中选用交叉验证法[21]来优化模型参数。
3 基于EMD和SVM的短期气候预测本文将经验模态分解与支持向量机的时序预测方法相结合, 即首先通过经验模态分解算法将标准化处理后的时间序列分解为多个IMF分量和1个趋势分量, 并对每一个分量分别构造了1个SVM模型进行预测, 再将预测结果线性合成最终的预测序列。
试验中的数据资料来自广西全区88个气象观测站49年 (1957—2005年)6—8月逐年降水量距平百分率序列。由于6—8月是广西主要的降雨季节, 也是广西容易发生洪涝灾害的季节, 因此准确地预测降水量的变化趋势有很大的实际意义。介于降水量的逐年波动幅度较大, 在使用EMD分解前需进行标准化处理。这里采用z-score标准化方法[22], 即
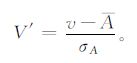
|
(9) |
式 (9) 中, v为原值, A和σA分别为序列的均值和标准差, 处理后得到标准化的距平百分率序列X(t)。使用EMD方法对X(t) 进行分解, 结果如图 1b所示。接下来, 将分解出的IMF1~IMF4分量以及Rn趋势分量通过构造不同的SVM进行预测。对每个SVM, 根据时序预测方法, 选择X(t) 中前40年的数据, 构成训练样本集{(xi, yi)|i=1, 2, …, 10}。其中xi包含30年数据, yi为对应后一年的值, 即
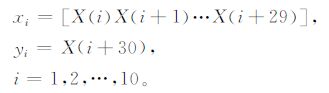
|
(10) |
预测X(t) 中后9个数据, 即1997—2005年的降水量, 并通过相对误差e和均方误差eav检验预测效果:
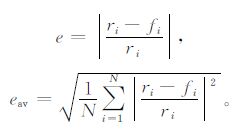
|
(11) |
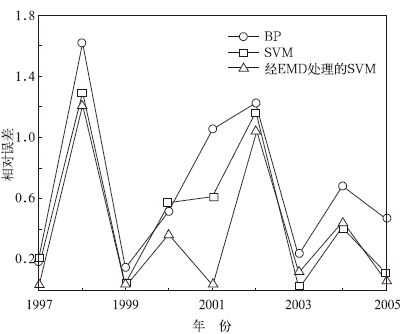
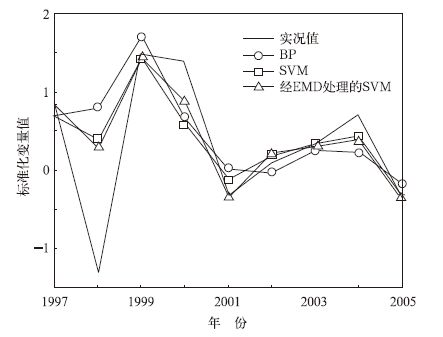
式 (11) 中, ri为实况值, fi为预测值。为了对比验证, 使用不经过EMD处理的BP神经网络和SVM算法进行预测。其中, BP神经网路采用单隐层结构, 隐层节点数设为8, 带有可变学习率和动量项系数。首先来看其拟合效果, 即用训练好的网络来预测这10组样本, 结果表明:运用3种方案均可达到接近100%的精度, 可见都具有很好的数据拟合能力。接下来进行预测, 所得相对误差和相对误差曲线图如表 1和图 2所示, 预测值与实况值的比较如图 3所示。
|
|
表 1 运用3种方案进行预测的相对误差 Table 1 The relative error of three schemes for forecast |
|
|
| 图 2. 运用3种方案进行预测的相对误差曲线 Fig 2. The relative error curve of three schemes for forecast | |
|
|
| 图 3. 预测值与实况值的比较 Fig 3. The comparison between predicted value and actual value | |
其中, 3种方案的均方误差分别为:0.8344, 0.6225和0.3681。
先比较SVM和BP神经网络方法。表 1中, 如果只对1997年做单步预测, 则BP神经网络方法的精度近似于SVM方法, 但随着步长的增加, 逐渐反映出了BP算法的不足。如在1998年和2001年, 降水量出现了明显的波动, 使得BP算法的误差均高出其他两种方法50%左右, 在预测曲线上表现为这一段更加平滑, 这暴露了BP算法的过学习性。在整体的误差变化中, 除了2000年, BP算法产生的误差几乎都是最大, 并且在2005年处还有增大的趋势。这说明了BP算法在处理类似于本文的小样本问题时, 泛化能力较弱, 而支持向量机算法以结构风险最小化为准则, 在样本数量有限的情况下可以更好地反映出变化规律。
经EMD处理后的SVM方法, 从误差曲线可以看出总体处理后趋势变化和原方法比较一致, 除2003年和2004年的误差略高, 其余年份都达到了更好的预测效果, 从均方根误差上可以更明显看出该方法的优势。说明EMD方法将原始序列分解为一系列具有平稳特性的分量, 反映出序列在不同时间尺度上的变化规律, 更适合于使用机器学习方法进行预测。而在对每个IMF分量分别使用SVM进行预测时, 较大的误差主要集中在IMF1和IMF2两分量中, 说明了由EMD处理出的高频分量有时仍带有一定的非平稳性, 在今后工作中需要对算法做进一步改善。
4 小结在对具有非线性、非平稳特性的气候时间序列进行短期气候预测中, 本文采用了经验模态分解方法, 对原始序列进行平稳化处理, 分解出若干IMF分量和一个趋势分量, 并分别对每个分量运用支持向量机算法进行预测, 将结果重构为最终的预测值。经过广西全区49年中的夏季降水量距平百分率数据测试, 验证了该方案的优越性, 能够更好地反映出降水量的变化趋势, 在短期气候预测领域具有较为广泛的应用前景。
| [1] | 张迎春, 肖冬荣, 赵远东. 基于时间序列神经网络的气象预测研究. 武汉理工大学学报 (交通科学与工程版), 2003, 27, (2): 237–240. |
| [2] | 金龙, 吴建生, 林开平, 等. 基于遗传算法的神经网络短期气候预测模型. 高原气象, 2005, 24, (6): 981–987. |
| [3] | 陈永义, 俞小鼎, 高学浩, 等. 处理非线性分类和回归问题的-种新方法 (I)--支持向量机方法简介. 应用气象学报, 2004, 15, (3): 345–354. |
| [4] | 冯汉中, 陈永义. 处理非线性分类和回归问题的一种新方法 (Ⅱ)--支持向量机方法在天气预报中的应用. 应用气象学报, 2004, 15, (3): 355–365. |
| [5] | 冯汉中, 陈永义, 成永勤, 等. 双流机场低能见度天气预报方法研究. 应用气象学报, 2006, 17, (1): 94–99. |
| [6] | 燕东渭, 孙田文, 杨艳, 等. 支持向量数据描述在西北暴雨预报中的应用试验. 应用气象学报, 2007, 18, (5): 676–681. |
| [7] | 刘科峰, 张韧, 洪梅, 等. 基于最小二乘支持向量机的副热带高压预测模型. 应用气象学报, 2009, 20, (3): 354–359. |
| [8] | 林振山, 汪曙光. 近四百年北半球气温变化的分析:EMD方法的应用. 热带气象学报, 2004, 24, (1): 90–96. |
| [9] | Huang N E, Zhcng Shen, The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Times Series Aanalysis. London, 1998: 903–995. |
| [10] | 黄伟, 杨志刚, 丁志宏. 基于EMD的官厅水库天然年径流量变化多时间尺度分析. 水资源与水工程学报, 2008, 19, (1): 49–52. |
| [11] | 李楠, 曾兴雯. 基于EMD和神经网络的时间序列预测. 西安邮电学院学报, 2007, 12, (1): 51–54. |
| [12] | 林瑞霖, 周平. 基于EMD和神经网络的气阀机构故障诊断研究. 海军工程大学学报, 2008, 20, (2): 48–51. |
| [13] | 钟佑明, 金涛, 秦树人. 希尔伯特-黄变换中的-种新包络线算法. 数据采集与处理, 2005, 20, (1): 13–14. |
| [14] | 黄大吉, 赵进平, 苏纪兰. 希尔伯特-黄变换的端点延拓. 海洋学报, 2003, 25, (1): 1–11. |
| [15] | Zhao J P, Huang D J, Mirror extending and circular spline function for empirical mode decomposition method. Journal of ZhejiangUniversity, 2001, 2, (3): 247–252. |
| [16] | 朱金龙, 邱晓晖. 正交多项式拟合在EMD算法端点问题中的应用. 计算机工程与应用, 2006, 23: 72–74. |
| [17] | 邓拥军, 王伟, 钱成春, 等. EMD方法及Hilbert变换中边界问题的处理. 科学通报, 2001, 46, (3): 257–263. |
| [18] | 于伟凯. EMD时频分析方法的理论研究与应用. 秦皇岛: 燕山大学, 2006. |
| [19] | 杜熊禹. 用于数据挖掘的支持向量机算法研究. 成都: 电子科技大学, 2007. |
| [20] | Suykens J A K, Lukas L, Vandewalle J, Least squares suppert vecter machine classifiers. Neural Processing Letters, 1999, 9, (3): 293–300. DOI:10.1023/A:1018628609742 |
| [21] | 董春曦, 饶鲜, 杨绍全, 等. 支持向量机参数选择方法研究. 系统工程与电子技术, 2004, 26, (8): 1117–1120. |
| [22] | HanJiawei, MichelineKamber. 数据挖掘概念与技术. 范明, 孟小峰, 译北京: 机械工业出版社, 2008: 46. |
 2010, 21 (3): 366-371
2010, 21 (3): 366-371


