2. 国家气候中心,北京 100081
2. National Climate Center, Beijing 100081
经过几十年的发展,数值天气预报取得了很大进步,天气形势的可用预报目前为5 7d[1-2]。在短期天气预报取得成功的基础上,世界上主要的数值预报中心均在努力研发各种技术来提高天气预报的准确率与时效。但目前对更长时间尺度,如6 15d预报技巧仍然很低,需要进一步提高预报能力[3]。
由可预报性理论研究可知,逐日预报的可预报期限不超过2 3周,15d以内的逐日预报在理论上是可行的[4-7]。但由于大气本身的不稳定性及非线性相互作用和模式误差的存在,使得预报误差随时间不断增大,以至5d以上逐日预报的可预报信息被掩盖,预报技巧偏低。为了减小数值模式的预报误差,主要有两个努力方向:一方面,通过改进观测和同化系统,减小初值的不确定性;另一方面,通过增加分辨率,改进物理过程和动力框架等使得数值模式更接近于实际大气。在发展数值模式的同时,利用历史资料订正数值模式预报结果的一系列统计经验方法被提出[8-9]。我国学者很早就提出了在数值预报中引入历史资料的重要性和可能性[10-11],围绕如何有效结合历史资料和动力模式,开展了一系列很有特色的研究[12-16]。一些科学家提出和发展了一种将天气学经验与动力预报相结合的相似-动力方法[17-23],该方法在简单的准地转模式和复杂的业务模式上均取得了成功,使预报准确率得到明显提高,显示出较好的应用前景。
相似-动力方法的困难在于相似场的选取,由于数值预报模式的自由度巨大 (107),要对这么大自由度变量在历史上找到很好的相似,在现有历史资料条件下很困难。为了避开这个困难,已有的研究[20, 22-23]用500hPa高度场来判别相似,但仅用一层资料不能很好地代表初值所处状态。同时,随着预报时间的增加,中小尺度的分量已不可预报,选取相似时仍保留该部分信息会对可预报分量产生干扰。已有研究表明[24-25],强迫耗散的非线性系统的长期行为会收缩到一个有限的自由度较少的吸引子上,初值在支撑低维气候吸引子的基上投影的自由度就会大大缩小,同时还能有效消除小尺度高频分量。因此,本文针对6 15d的预报时段,通过压缩自由度,提出了一种新的初始场相似判别方法,定义了多变量的综合相似指数。基于该定义分析初值相似程度与其误差演变之间的关系,并将该方法与用单一500hPa高度场来判别相似进行比较。此外,还分析了相似初值间模式预报误差的空间分布特征。初步试验表明:利用相似初值的模式预报误差具有相似性特点,相似-动力方法能有效提高模式的预报技巧,为进一步改进6 15d数值天气预报提供支持。
1 原理与方法大气是强迫耗散的非线性系统,理论上讲,在外源强迫下,大气会向外源非线性适应,它的长期行为会收缩到一个有限的自由度较少的吸引子上。数学上就是从高维相空间向低维吸引子演化,耗散使众多小尺度变量变为无关变量,最后剩下支撑吸引子的少数自由度。利用已经掌握的大量历史天气资料能找到一组支撑该吸引子的正交基。由于这组基是支撑低维气候吸引子的,其自由度大大减小。同时,某一气象要素场在这组基上的投影将不再包括那些小尺度、高频的快变分量[3, 24-25],为延长数值天气预报时效提供了可能。
1.1 压缩自由度一组支撑气候吸引子的正交基可以通过经验正交函数 (EOF) 来获取[24-25]。对Rm空间而言,存在着h个线性无关向量 (h < m),它所张开的子空间覆盖了吸引子,即用前面h个特征向量就可以准确地描述气象要素场在气候吸引子上的状态。这样就得到了一组Rh空间的标准正交基。在考虑了下垫面外界强迫等因子的季节变化和年际变化后,经验正交函数对大气要素场的展开精度是稳定的[26]。将该原理与方法应用到月延伸期预报中,预报技巧有明显改进[25]。
对模式变量在6 15 d预报时段内30年 (1971—2000年) 的各层逐日谱系数距平场Ψm×n进行EOF分解。记为
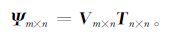
|
(1) |
式 (1) 中,m,n分别为空间点和时间点,Vm×n为标准化正交基,即特征向量,Tn×n为时间系数,即主分量。为简单起见,可由累积解释方差大于一定阈值的前h个主分量来反映原变量场变化的大部分信息,以此减小初值的维数。简便起见,这里取累积方差贡献率达到80%时的特征向量个数,而把其余的特征向量认为是随机误差造成的。即
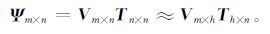
|
(2) |
同时,各变量垂直层之间也存在相关性,为了消除该相关性,进一步缩小自由度,再将各变量所有层的前几个主分量的矩阵进行组合,记为Tp×n(p=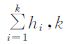
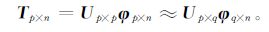
|
(3) |
式 (3) 中,Up×p为标准化正交基,φp×n为时间系数。
最终可将k层的Ψm×n减小自由度到φq×n上。某一时刻初始场的各变量可分别由各自的支撑气候吸引子基底V和U依次展开,得到压缩自由度后的初始场。即
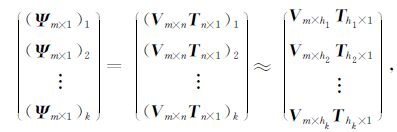
|
(4) |
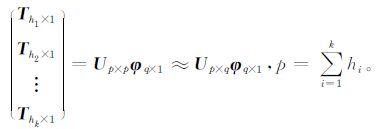
|
(5) |
减小自由度后,对初值的各变量可用较小自由度的φq×1来近似代表原变量所有层的异常状态。将j时刻的第i个主分量进行标准化,有
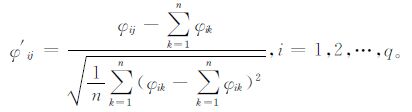
|
(6) |
那么两个场之间的相似指数(I)可定义为:
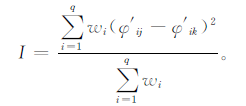
|
(7) |
式 (7) 中,j和k分别代表两个时刻的场,wi为各个主分量的权重,取各主分量的解释方差。分别计算出每个变量的相似指数,取其平均为整个初始场的相似指数,即初值相似指数 (IA)。相似指数越小,表示两个场越相似。
误差相似指数 (Ie) 的计算与初值相似指数的计算类似,但为了体现不同预报时间误差相似指数之间的差异,式 (6) 的分母依然用观测资料各个主分量的方差。如果初值相似指数与对应的误差相似指数值相当,则表示误差场之间的差异和初始场之间的差异很接近,相似初值提供的误差信息就无意义了。值得注意的是,这里定义的初值相似指数和误差相似指数都是在气候吸引子上,滤去了小尺度分量。
2 结果和分析 2.1 模式和资料本文所用的大气环流模式是国家气候中心月尺度动力延伸业务预报模式T63L16,该模式采用全球谱模式形式,水平方向采用三角形截断 (近似于1.875°×1.875°),垂直方向为16层,采用η混合坐标系[27]。
初始场使用的是T63模式所需的同化后的谱系数资料,可近似视为观测资料。大气部分包含每日4次 (00:00(世界时,下同),06:00,12:00和18:00) 的涡度、散度、温度、比湿和地面气压对数5个变量,本文用16层涡度、散度、温度和比湿的12:00资料。误差场是为观测场与模式预报场之间的差,仍是5个变量,每24h输出1次,由于初值的相似性会随积分时间而衰减,更新相似场和误差订正的时间间隔要小于5d,为了节省计算量,本文只计算了1 5d的预报误差。500hPa高度场采用NCEP/NCAR再分析资料。
2.2 初值相似与误差相似的关系大气本身的不稳定性会导致误差增长,意味着初始很小的误差,都将不可避免地在一段时间后导致天气预报技巧完全丧失,即对初值很敏感。集合预报结果也表明,很相近的集合初值经过一段时间后预报结果可能会差异很大。但同时也应该注意到,即使在误差增长最快的一些方向上加入了初始扰动,其预报结果中仍有很多一致的部分。因此,集合平均通过滤掉预报中不确定成分,保留集合成员中一致部分的倾向能提高预报质量。集合预报结果表明有些分量在预报时段内差异很小,即这些分量在初值上的差异并没有显著放大,为模式在该时段内的可预报分量。因此,初值在可预报分量上的投影如果很接近,那么在预报时段内,由于其初始误差并不显著增长,预报误差也会很接近。
从上面的分析可以看出,对差异很小的集合预报初值,在可预报分量上其误差具有一致性,那么对历史相似而言,模式预报误差是否有着类似的关系?为了考察初值相似时,其对应的模式预报误差间的相近程度,使用国家气候中心T63L16大气环流模式进行逐日预报试验来探讨。
本文围绕利用相似-动力方法提高6 15d数值预报而进行研究,该方法中误差订正间隔一般为24h,即在初始时刻选取相似参考态,以相似参考态24h的预报误差来订正模式预报24h的误差,用订正后的预报值重新选取相似,进而可估计下一个24h的预报误差 (但由于计算量的原因,考虑到大气状态特征存在一段时间的持续,因此订正后的24h预报值的相似参考态直接取初值相似参考态24h后的实况值,并以此为初值,估计下一个24h的预报误差,每隔5d利用订正后的预报值重新选取相似),依此循环,直至预报结束[21]。因此这里只分析1 5d的预报误差情况,特别是24h的预报误差。
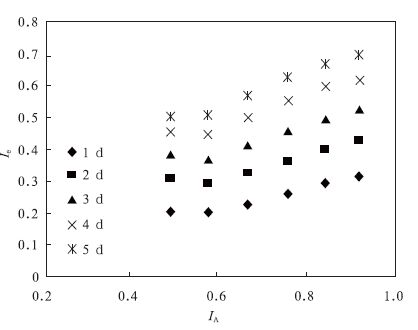
为了减少计算量,以1月为例,对1971—2000年的1月1—30日12:00的观测资料用式 (1) (3) 的方法压缩自由度。为了从整体上给出相似初值间模式预报误差的演变情况,用式 (4) (7) 计算1968—2008年的1月14—18日两两之间的初值相似指数和预报误差相似指数,舍去同一年两两之间的结果。图 1给出了1 5d预报误差的相似指数随初值相似指数的变化。为了避免随机性的影响,将初值相似指数分为0.4 0.5,0.5 0.6,0.6 0.7,0.7 0.8,0.8 0.9和0.9 1.0共6段。横坐标为各段初值相似指数 (IA) 的平均值,纵坐标为预报误差相似指数 (Ie) 的平均值。从图 1中可以看出,1 5d的误差相似指数都随着初值相似指数的增大而增大,表明初值越相似,预报误差的相似性越高,即两个很相近的初始状态,在较短时间内预报误差有很好的一致性。误差的相似性随预报时效延长而减小,当预报时效达到5d时,误差相似指数和初值相似指数相当,表明相似初值提供的误差信息已经非常有限了,因此订正间隔应小于5d,并在此时用预报场重新选取更相近的相似状态是必要的[23]。
|
|
| 图 1. 1 5d预报误差的相似指数随初值相似程度的演变 Fig 1. The evolution of analogue index of forecast error with the analogue degree of initial value | |
针对如何减小预报误差,除了改进数值模式外,模式误差订正技术也得到了很大发展,它主要通过两种方式进行,一是后处理订正,另一种则是过程订正。后处理订正没有考虑预报过程中内部误差和外部误差的非线性相互作用,而过程订正通过将短期的预报误差看作是模式状态的函数,从而实现在积分过程中逐步订正预报误差,阻止预报误差增长。然而,数值模式的预报误差依赖于初始流型,为了考虑模式误差的流型依赖性,常采用统计方法建立预报误差与模式变量的联系[28],这类方法需要预先设定二者间的函数形式,用最优估计方法确定函数中的各个参数,使其对训练样本的拟合最佳,原理和统计上的回归方法类似。实际上,预先设定的函数形式是否为误差和模式变量真实关系的合理描述需要研究,且这种函数形式具有模式依赖性,不便于移植。在相似-动力方法中,利用历史相似提供的预报误差对预报误差进行预报,不但考虑了模式的系统性误差,还包含了与相似初值相近流型的模式误差演变信息。同时,压缩自由度后,仅保留了可预报性更强的大尺度分量,即误差增长较为缓慢的分量。大尺度分量上差异较小的相似初值,其模式预报误差的演变也具有较高的相似性,依此订正预报误差,而不涉及预报误差与模式变量统计具体的函数形式,避免了直接建立预报误差与模式变量统计联系的困难。
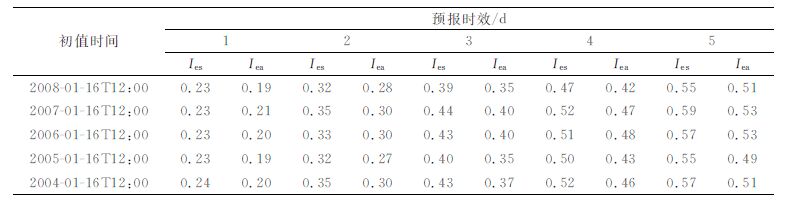
有研究表明,在积分过程中引入定常的系统误差就能起到改进预报技巧的作用[28]。为了进一步说明用相似初值的模式预报误差对实际预报误差进行估计的有效性,比较了起始个例预报误差与历史相似个例预报误差、系统误差之间的相似程度。不失一般性,本文以2004—2008年的1月16日12:005个个例作为初值选取相似,选取范围为1968到初值所在年份的前一年,所在日期的前后15d,如2008年1月16日的选取范围为1968—2007年的1月1—31日,取4个最好相似个例的平均预报误差为相似个例的预报误差。相似选取范围内全部个例的预报误差平均定义为系统误差,近似代表了气候漂移。表 1给出了起始个例预报误差与相似个例预报误差 (Iea)、系统误差 (Ies) 的相似指数随预报时间的演变。从表 1可以看出,对5个个例,相似个例的预报误差均比系统误差更接近于起始个例的预报误差。同时,相似个例与起始个例预报误差的接近程度存在差异,2008年、2004年和2005年选到的相似程度较高,4个最优历史相似个例的平均相似指数分别为0.49,0.50和0.51,2006年和2007年选到的相似程度较低,相似指数为0.53和0.52。比较初值相似指数和预报误差相似指数可以看出,2008年和2005年的起始个例与相似个例预报误差更接近的原因是其初值相似性更高,而2006年和2007年的两个个例初值相似性要差一些。说明预报误差的相似程度与初值间的相似程度密切相关,初值间的相似指数越小,预报误差的一致性也就越高。对在历史资料中能找到很好相似的个例,相似-动力方法能有效减小预报误差,相反,某些极端事件的个例很难找到历史相似,该方法的订正效果可能会不明显。但已知初值间的相似程度,可对相似-动力方法预报结果的可信度进行预报。
|
|
表 1 起始个例预报误差与相似个例预报误差、系统误差的相似指数随预报时长的演变 Table 1 The evolution of analogue index of forecast error on initial case, analogue case and system error with leading time |
2.3 与500hPa高度场选取相似的比较
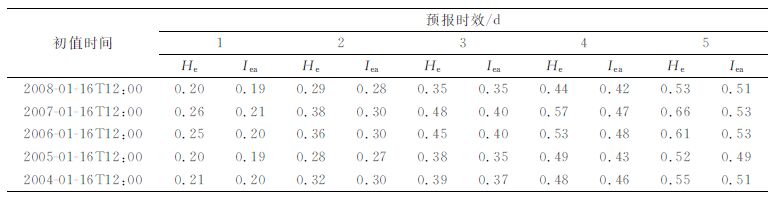
已有研究表明,用500hPa高度场判别的相似初值,在一定时间内,模式预报误差演变仍有相似性[29],利用这种相似性,在积分过程中订正预报误差取得了较好的预报效果[20-22]。但是,仅用500hPa高度场选取相似显然不能表示大气的整体状态。下面用本文定义的相似指数和用500hPa高度场分别选取相似,比较误差相似指数的变化情况。不同时刻500hPa高度场之间的相似程度用欧氏距离来度量[22],距离越小越相似,历史相似选取范围与前面一致。这里仍用2004—2008年的1月16日12:00作为初值,分别用相似指数和500hPa高度场各选取4个最好相似,分析其误差演变情况,结果参见表 2,500 hPa高度场选取的相似场对应的模式预报误差相似指数用He表示。5个个例均表明,用本文采取的相似指数方案要优于仅用500hPa高度场选取的相似,说明用初值中所有变量的信息比仅用500hPa高度场更能代表初值所处的状态;同时,由于用500hPa高度场选取相似,没有考虑不同尺度分量的可预报性问题,包含了不可预报的中小尺度分量,而这部分分量对初值敏感,即使初始状态很相近,但模式预报误差仍可能不具有相似性。
|
|
表 2 两种相似选取方案估计的预报误差与实际预报误差相似指数随预报时长演变 Table 2 The comparison of the evolution of analogue index of estimated forecast error and real forecast error with leading time |
2.4 预报误差相似性的空间分布
为了考察起始个例预报误差与历史相似个例预报误差的空间分布特征,以温度场为例,图 2给出了2008年1月16日12:00的起始个例及其4个相似个例24h预报误差的对比分析。从图 2可以看出,在模式第7层 (约453hPa),起始个例和4个相似个例的预报误差有很高的相似性,在全球大部分地区为大片的负值区,空间分布和误差大小都非常接近;中低纬度地区的误差分布相对均匀;在北半球高纬度地区都有两个明显的正值区,分别位于中西伯利亚北部和北美大陆的北部,误差大小相当,1999年的个例误差略偏大。4个相似个例在白令海峡均存在正误差中心,但2008年个例的正误差中心很弱。南半球高纬度地区存在一些小的正误差中心,5张图的区域和大小都很接近。总的来说,用4个相似个例估计的预报误差与起始个例预报误差的相似性很明显。

|
|
| 图 2. 2008年1月16日12:00及其4个最相似个例在η=7层 (约453hPa) 的24h温度场预报误差 Fig 2. 24-hour forecast error of temperature at η=7 (about 453 hPa) at 12: 00 16 January 2008 and its first 4 analogues | |
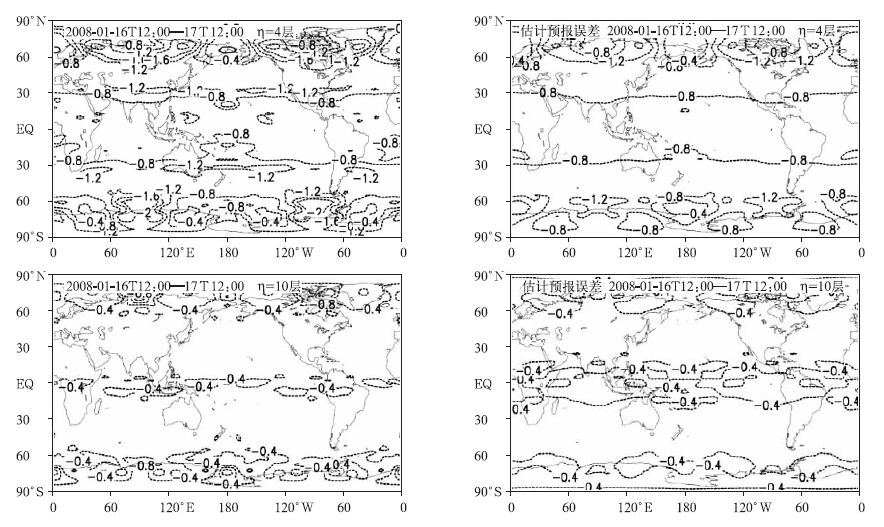
图 3给出了第4层 (约216hPa) 和第10层 (约735hPa) 起始个例和4个相似个例估计的24h预报误差的空间分布图。从图 3可以看出,和第7层的结果类似,在第4层,4个相似个例估计的预报误差,不论是中心还是大小,都与起始个例的预报误差非常接近。而第10层差异稍大,起始个例有3个误差中心,分别位于北半球高纬度地区的中西伯利亚北部、白令海峡和北美大陆北部,但相似个例估计的预报误差中这3个中心均不存在,同时,对南半球的误差中心也估计偏弱,这可能与模式在各垂直层的预报技巧不同有关。由于在选取相似时考虑了所有层次的情况,因此这种误差的相似性在各个层次都存在,订正后能提高模式在各层的预报效果,改进模式的整体预报能力。
|
|
| 图 3. 2008年1月16日12:00及其4个最相似个例估计的24h温度场预报误差 (η=4层,约216hPa; η=10层,约735hPa) Fig 3. 24-hour forecast error of temperature at 12:00 16 January 2008 and its first 4 analogues (η=4, about 216hPa; η=0, about 735 hPa) | |
综上所述,起始个例与相似个例的预报误差具有很好的相似性。可预报性研究表明,大尺度具有更高的可预报性,即大尺度上初始很小的扰动其预报结果的差异不会显著放大。压缩自由度后,不包含小尺度的分量和特征,在大尺度分量上很接近的相似初值,在较短的预报时效内,预报误差的差异不会显著放大,因此具有较好的相似性。利用这种相似性对模式的预报误差进行预报,有望改进模式的预报技巧。同时,各分量误差的相似性与初值差异程度和各分量的可预报期限密切相关。
2.5 数值试验为了进一步论证相似初值间模式预报误差的相似性及相似-动力方法利用这种相似性改进预报技巧的有效性,利用数值模式进行了预报试验。本文以2004—2008年的1月16日12:00的5个例为例,用相似-动力方法进行了6 15d预报,给出了初步的预报技巧检验。
预报方案 (ANA) 如下:前5d直接由T63模式预报获得;从第6天开始,每24h用式 (4) 和式 (5) 压缩自由度,式 (6) 和式 (7) 用于选取相似参考态;以4个最优相似参考态的24h预报误差的算术平均估计预报误差;用估计的预报误差订正模式预报;用订正后的预报值重新选取相似,进而可估计下一个24h的预报误差,并进行订正 (由于计算量的原因,同时考虑到大气状态特征存在一段时间的持续,因此订正后的24h预报值的相似参考态直接取初值相似参考态24h后的实况值,并以此为初值,估计下一个24h的预报误差,每隔5d利用订正后的预报值重新选取相似); 依此循环,直至预报结束。用T63模式直接积分15d,不进行任何处理作为控制试验 (CTRL)。检验用距平相关系数 (ACC) 和均方根误差 (RMSE) 评分。
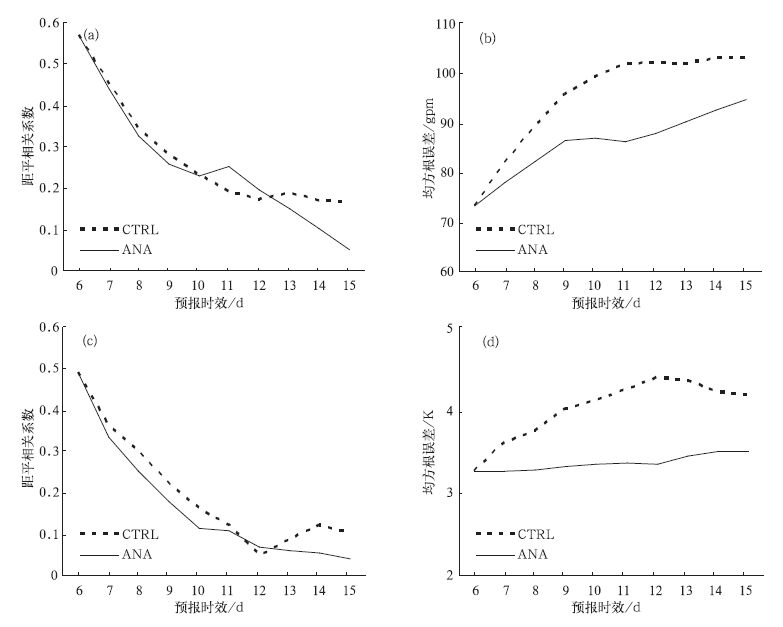
表 3给出了5个个例平均的全球6 15d平均500hPa高度场和温度场的预报评分,可以看出,500hPa高度场和温度场的距平相关系数和控制试验相当,均方根误差分别减小了5.5gpm和0.6K。这可能与本文选取相似的方法有关,仅考虑了数值的接近程度,而未考虑空间分布型的相似性,这有待深入研究。不同尺度的波 (即纬向Fourier展开的波数) 均方根误差减小的程度不同,500hPa高度场纬向1 3波的超长波改进最明显,均方根误差减小了8.4gpm对天气尺度的波 (4 9波) 改进较小,0波甚至略差于控制预报。500hPa温度场则对天气尺度以上波的均方根误差均有改进,0波改进大,减小了0.6K。
|
|
表 3 5个个例平均的全球6~15d平均500hPa高度场和温度场的预报评分 Table 3 6—15-day average score of 5 cases of 500hPa geopotential height and temperature |
图 4给出了全球500hPa高度场和温度场的逐日预报与实况的ACC和RMSE,可以看出,与控制预报相比,ACC在大部分时间略低于控制预报,这与表 3一致。不论是对高度场还是温度场,相似动力方法的RMSE都得到了明显的减小。这说明利用相似初值的模式预报误差具有相似性的特点,能有助于消除相当一部分预报误差。
15d以内的逐日预报在理论上是可行的,在该时间范围内,天气尺度以上的分量是可预报的,因此,可用数值模式进行确定性预报,而对天气尺度以下的小尺度分量,由于受到可预报性的限制,确定性预报将不再可行,必须转为概率预报。本文的误差订正只对不包含小尺度分量的部分进行,初步试验表明:能有效改进大尺度可预报分量的确定性预报,避免了小尺度分量预报误差的快速增长对预报效果的影响,当然,针对可预报分量确定性预报的订正,与可预报分量的多寡密切相关,就6 15d而言,由于天气尺度以上是可预报的,可预报分量的预报误差在总的预报误差中占有相当大的比例,结合历史资料,用统计方法减小该部分的预报误差,有助于提高预报模式的预报性能,初步的检验结果证实了这点。下一步将在预报过程中引入不可预报分量的概率预报,以达到对可预报分量和不可预报分量采用不同的预报方案和策略。值得注意的是,本文相似选取和误差订正是针对模式的所有变量和层次进行的,因此预报结果的改善对各个变量的各个层次都存在。同时,下一步将对特定的预报变量 (如500hPa高度场),采用有针对的相似选取和误差订正方案。
|
|
| 图 4. 5个个例平均的500hPa高度场的逐日预报与实况的距平相关系数 (a),均方根误差 (b) 和500hPa温度场的逐日预报与实况的距平相关系数 (c),均方根误差 (d) Fig 4. The daily ACC averaged over 5 cases of 500hPa geopotential height (a) andtemperature (c), and thedaily RMS Eaveraged over 5 cases of 500hPa geopotential height (b) and temperature (d) | |
3 结论与讨论
对中期天气预报,普遍共识是以数值模式为主,同时结合统计的优点能有效提高预报水平。相似-动力方法是结合统计和动力的最优方法之一,但该方法面临的困难之一是由于自由度太大,相似场选取困难。本文通过在支撑气候吸引子的基上压缩自由度,提出了一种新的相似判别方法。这种方法减小了自由度,避免了自由度太大选取相似的困难;同时,气象要素场在气候吸引子支撑基上的投影将不包括小尺度的快变分量,避免了混沌分量对初值敏感的问题,使得初值的相似性得以持续。基于该方案分析初值相似程度与其误差演变之间的关系,并与用单一500hPa高度场来判别相似进行比较。分析表明,误差的相似程度与初值的相似程度成正比,相似初值提供的预报误差信息很接近于实际的预报误差。初值越相似,其短期误差演变的相似性也越高,这证实了相似-动力方法的有效性,为进一步提高数值预报技巧提供了支持。这类途径可不从正面改进数值模式的动力框架、物理过程、计算方案等,而从历史资料的角度亦能有效获得数值模式的预报误差信息,达到提高预报技巧的目的。与已有的用500hPa高度场选取相似相比,模式初值在气候吸引子上的相似更能代表整个初始场状态的相似。同时,在空间分布特征上,相似初值间的模式预报误差也有很好的一致性。初步试验表明,利用相似初值的模式预报误差具有相似性的特点,相似-动力方法能有效提高模式的预报技巧,为进一步改进6 15d数值天气预报提供支持。
理论研究表明,当数值预报模式完全准确时,相似-动力方法的预报结果蜕化为动力学方法的预报结果,当历史相似完全准确时,蜕化为统计学方法的预报结果。因此,相似-动力方法依赖于数值模式,随着数值模式的不断改进,能更好地描述预报时段内实际大气的可预报分量,相似-动力方法也将有更好的应用前景。同时也应注意到,本文是从观测资料中提取支撑气候吸引子的正交基,滤除掉小尺度分量,基向量个数的截取仍待研究。此外,在当前的模式条件下,由于模式的缺陷,并不是对观测资料中的所有大尺度信息都是可预报的,具有模式依赖性,对所用模式的可预报分量也有待进一步研究。
| [1] | Simmons A J, Hollingsworth A, Someaspects of the improve-ment in skill of numericalweather prediction. Quart J Roy Mete-orol Soc, 2002, 128: 647–677. DOI:10.1256/003590002321042135 |
| [2] | 陈德辉, 薛纪善. 数值天气预报业务模式现状与展望. 气象学报, 2004, 62, (5): 623–633. |
| [3] | 丑纪范, 谢志辉, 王式功. 建立6-15天数值天气预报业务系统的另类途径. 军事气象水文, 2006, (3): 4–9. |
| [4] | Lorenz E N, A study of the predictability of a 28-variable at-mospheric model. Tellus, 1965, 17: 321–333. DOI:10.1111/tus.1965.17.issue-3 |
| [5] | Lorenz E N, Atmospheric predictability experiments with a large numerical model. Tellus, 1982, 34: 505–513. DOI:10.1111/tus.1982.34.issue-6 |
| [6] | Ding R Q, Li J P, Nonlinear finite-time Lyapunov exponent and predictability. Physics Letters A, 2007, 364: 396–400. DOI:10.1016/j.physleta.2006.11.094 |
| [7] | Mu M, Duan W S, Xu H, Applications of conditional nonlinear optimal perturbation in predictability study and sen-sitivity analysis of weather and climate. Advances in Atmospheric Sciences, 2006, 23: 992–1002. DOI:10.1007/s00376-006-0992-3 |
| [8] | Glahn H R, Lowry D A, The use of model output statistics(MOS)in objective weather forecasting. Journal of Applied Meteorology, 1972, 11: 1203–1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2 |
| [9] | Hamill T M, Whitaker J S, Probabilistic quantitative precipi-tation forecasts based on reforecast analogs:Theory and ap-plication. Monthly Weather Review, 2006, 134: 3209–3229. DOI:10.1175/MWR3237.1 |
| [10] | 顾震潮. 天气数值预报中过去资料的使用问题. 气象学报, 1958, 29, (3): 176–184. |
| [11] | 丑纪范. 为什么要动力-统计相结合?--兼论如何结合. 高原气象, 1986, 5, (4): 367–372. |
| [12] | 郑庆林, 杜行远. 使用多时刻观测资料的数值天气预报新模式. 中国科学a辑, 1973, 16, (3): 289–297. |
| [13] | 曹鸿兴. 大气运动的自忆性方程. 中国科学b辑, 1993, 23, (1): 104–112. |
| [14] | 封国林, 曹鸿兴, 谷湘潜. 一种提高数值模式时间差分计算精度的新格式--回溯时间积分格式. 应用气象学报, 2002, 13, (2): 207–217. |
| [15] | 陈伯民, 纪立人, 杨培才. 改善月动力延伸预报水平的一种新途径. 科学通报, 2003, 48, (5): 513–520. |
| [16] | 曹鸿兴, 谷湘潜. 自忆谱模式制作中期天气预报的试验. 应用气象学报, 2000, 11, (4): 455–466. |
| [17] | 邱崇践, 丑纪范. 天气预报的相似-动力方法. 大气科学, 1989, 13, (1): 22–28. |
| [18] | 黄建平, 王绍武. 相似-动力模式的季节预报试验. 中国科学b辑, 1991, 21, (2): 216–224. |
| [19] | Huang J P, Yi Y H, Wang S W, Ananalogue-dynami-cal long-range numerical weather prediction system incorpora-ting historical evolution. Quarterly Journal of the Royal Meteorological Society, 1993, 119: 547–565. DOI:10.1002/(ISSN)1477-870X |
| [20] | 鲍名, 倪允琪, 丑纪范. 相似-动力模式的月平均环流预报试验. 科学通报, 2004, 49, (11): 1112–1115. |
| [21] | 丑纪范, 任宏利. 数值天气预报--另类途径的必要性和可行性. 应用气象学报, 2006, 17, (2): 240–244. |
| [22] | Gao L, Ren H L, Li J P, Analogue correction method of errors and its application to numerical weather prediction. Chinese Physics, 2006, 15, (4): 882–889. DOI:10.1088/1009-1963/15/4/038 |
| [23] | 任宏利, 张培群, 李维京. 基于多个参考态更新的动力相似预报方法及应用. 物理学报, 2006, 55, (8): 4388–4396. |
| [24] | 张邦林, 丑纪范. 经验正交函数在气候数值模拟中的应用. 中国科学b辑, 1991, 21, (4): 442–448. |
| [25] | 张培群, 丑纪范. 改进月延伸预报的一种方法. 高原气象, 1997, 16, (4): 376–388. |
| [26] | 张邦林, 丑纪范. 经验正交函数展开精度的稳定性研究. 气象学报, 1992, 50, (3): 342–345. |
| [27] | 董敏. 国家气侯中心大气环流模式--基本原理和使用说明. 北京:气象出版社, 2001: 5–15. |
| [28] | Danforth C M, Kalnay E, Miyoshi T, Estimating and correc-ting global weather model error. Monthly Weather Review, 2007, 135, (2): 281–299. DOI:10.1175/MWR3289.1 |
| [29] | 任宏利, 封国林, 张培群. 论动力相似预报的物理基础问题. 地球科学进展, 2007, 22, (10): 1027–1035. |
 2010, 21 (2): 139-148
2010, 21 (2): 139-148