2. 中国气象科学研究院, 北京100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081
动力气象学理论在区分了不同动力过程的时空尺度之后得到了快速发展,尺度分析作为一种手段奠定了大气动力学基础,而时空尺度概念也由此成为动力气象学发展到相当高度的标志之一。对各种尺度天气现象及其大气动力学性质和规律的认识成为动力气象的主要任务,而数值模拟和数值天气预报则是实现这一认识过程的手段和实践应用。20世纪20年代,Richardson[1]首次数值预报失败正是对大气动力过程的多尺度性缺乏充分认识而致。到20世纪中叶,Charney等[2]则针对天气尺度过程采用简化的动力方程组成功给出了500hPa高度和涡度预报场。随着大气动力学和计算数学理论的发展,人们认识到大气动力的非线性和数值计算的稳定性问题直接导致了Richardson数值预报的失败,而大气的动力学特性与天气系统的时空尺度密切相关已经成为众所周知的事实。
就数值预报的时间尺度来讲,3d内的短期、两周以内的中期数值预报和月季尺度的长期数值预报机理不同,所采取的方法也应不同。由于大气动力过程的非线性和混沌现象的存在,中、长期数值天气预报和气候预测不可能在确定论的框架下实现,集合预报技术和动力统计预报[3-5]提供了处理这一尺度预报的可行方案。本文将撇开1周以上的预报,针对短、中期数值天气预报的发展来介绍多尺度数值预报模式发展的趋势和一些新的计算技术方案。
从20世纪50年代首次数值预报[2]成功后,数值预报模式开始逐步向多样化、复杂化发展。60年代大气环流模式出现,其后也成功地开发了海洋环流模式。从70年代后期的全球和区域预报模式,到80年代的云系可分辨模式、大涡模拟,以及耦合大气海洋模式等,模式的动力和物理过程不断复杂化、精细化、多样化、丰富化,而且计算网格也随着计算机的进步而不断缩小。特别是进入21世纪,以日本地球模拟器为代表的巨型机的计算能力达到每秒几十万亿次,数值模式向全球和细网格发展[6],从而模糊了大气环流模式和中尺度大气动力模式的区别,出现了全球中尺度模式和数值模拟。
由于计算能力和计算技术的进步,近年来多尺度预报和模拟的概念开始在气象领域流行。当初计算能力和计算理论薄弱,气象学不得不采用尺度分离方法研究大气现象,这种方法推动了大气动力学的发展。但随着计算技术和处理能力的提高,在短、中期数值预报领域采用精细多尺度模式模拟/预报的外部条件已经成熟,各个国家也在不断努力开发通用模式,包括我国的GRAPES模式[7-9]。大气运动本身就是多种尺度大气动力过程相互作用的统一,能量分布也是在运动过程中实现了各种尺度间的相互转换,数值模式正从界定时空尺度的单一模式向通用多尺度模式回归。就数值模式本身而言,如何构造多尺度大气模式成为大家关心的问题。本文结合当前最新研究成果,从网格设计、计算方法及其动力学性质、物理过程等几个方面予以介绍,从而探讨我国多尺度数值预报系统未来发展的方向和任务。
1 水平网格配置和球面网格系统模式水平网格上的变量分布形式对模式的动力学性质有很大影响,所以建立模式时应首先考虑该问题。早在1977年,Arakawa等[10]就对平面上给出了5种变量分布形式,即A,B,C,D和E网格,并在模式计算中给出了离散化方法讨论。此后,这些网格被大气模式广泛采用,特别是Arakawa-C网格近年成为大气数值模式的主流,这主要是因为它对罗斯贝变形半径较大流体有较好的频散性质和在计算散度和涡度时的便利性和高精度等优点的存在。
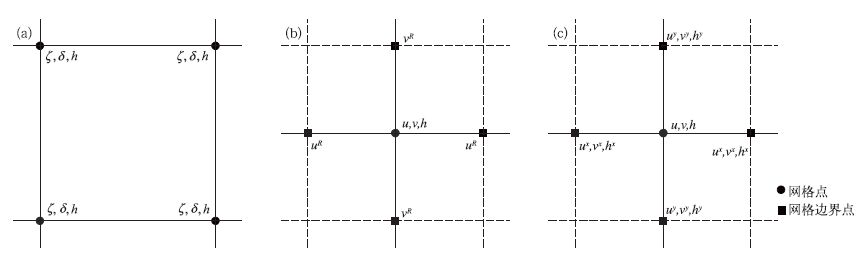
Randall[11]从频散关系讨论了这几种网格和一种Z网格 (图 1a) 的动力学性质,指出Arakawa-A网格在低分辨率具有较好的频散关系,而C网格则在高分辨率时具有较好的表现。对于Z网格,采用散度和涡度代替水平风作为预报变量,不论对于高分辨率还是低分辨率都有很好的频散性质,所以对于谱模式是一种极好的选择。可见,Arakawa-A和C网格对于同一个模式在不同分辨率情况下应用时并不能都保证有好的动力学效果,而Z网格虽然较好,但对一般以水平风速u,v为变量的格点模式应用起来并不方便。McGregor[12]又提出了一种R网格 (图 1b) 分布,实际上是对Arakawa-A网格的一种改造。即在A网格的边界上增加风场的 (类似C网格) 跳点风分量配置,但跳点风分量非直接通过动力计算获得,而是采用高阶特殊插值计算获得,并可以保证非跳点网格点和跳点网格点上风场的等价转换。这种方法可以应用跳点上的风场计算模式重力波相关项,无论在相对于Rossby变形半径的大网格还是小网格上对该网格上的波动频散特性都有很大改进。但是,边界上风速插值的计算破坏了波动在平面上的对称性,也增加了额外的计算。
|
|
| 图 1. Z网格 (a)、R网格 (b) 和M网格 (c) 示意图 Fig 1. SchematicplotsoftheZgrid (a), Rgrid (b) and M grid (c) | |
Xiao等[13]定义了一种多变量矩 (multi-mo-ment) 的网格分布,简称M网格 (图 1c)。这种网格通过在网格的边界和角点上附加变量矩,使单一网格上的信息量大增,从而增强每一个网格上变量的动力特性描述。这种网格对网格体积内定义体积积分平均值 (即图 1c中的●点变量),在网格边界上定义面积积分平均值,还可以在边界线上定义线积分平均值 (即■点值),也可以在点上定义变量 (图中虚线交点,本文没有定义),这就得到一组多变量矩的变量。从数学上来讲就可以在一个单一网格上构造高阶的变量插值函数,提高计算精度。对于二维网格,最简单的M网格就是定义了网格内面积平均量和在边界上定义了线积分平均量 (图 1c) 的系统。
对线性化浅水波方程采用波动解,在M网格上的解析结果显示,这种网格配置无论网格距大或者小都具有较好的数值频散[13],这与Z网格具有相似的频散关系。也就是说,在M网格上数值频散的解析解和线性浅水波方程的解析频散关系非常接近,对各种波段的波都具有很好的刻画能力。而且,这种网格的变量配置较简单,可以构造高阶的数值计算方案,适用于CIP-CSLR,PRM和PPM等多变量型半拉格朗日平流方案。对比R网格和M网格结构可以发现,两种网格的类似点就是在非跳点网格上增加了一个跳点网格的风场变量,可以用来计算重力波相关项。同时,保持了非跳点网格上的风场计算,从而同时获得跳点和非跳点网格的频散特性。所不同的是R网格基本上基于数学插值计算获得跳点风场,而M网格中的积分量则是基于数学计算和模式动力强迫两方面的控制,更具客观性。
从大气动力学各种尺度现象相互作用的理论基础出发,为了更好地描述地球大气各种尺度现象,应采用全球数值模式,否则模式将无法描述行星尺度的大气动力过程,同时全球模式也不必考虑侧边界条件的问题。对于全球模式而言,球面网格的选取当然成为制约模式性能的关键,比如常规经纬度坐标由于极点的奇异性使矢量场表达出现困难,且经度线随纬度升高而收缩使模式网格距随纬度减小,稳定的积分时间步长受到限制,积分计算时间大幅度增加。而采用准均匀网格的优点在于可以方便地提高或降低模式分辨率,更适合于多尺度预报和模拟。因此,采用准均匀的网格系统成为多尺度模式开发的追求之一。
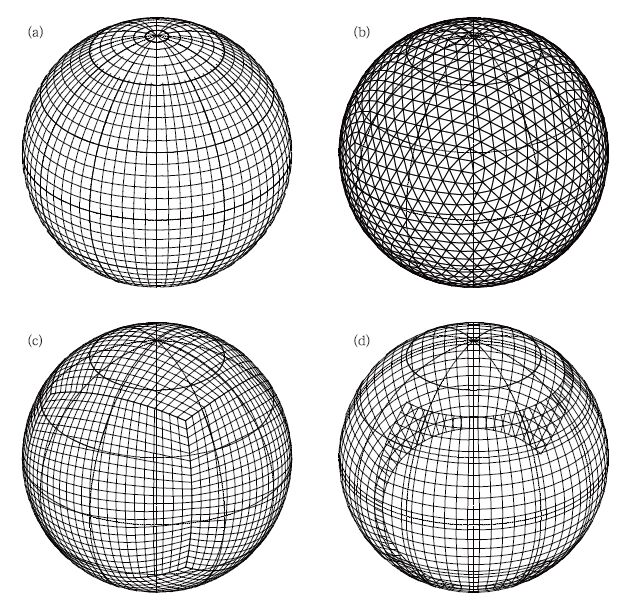
目前较为常用的球面网格有常规经纬度网格、递减经纬度网格、正方体网格、正二十面体网格、阴阳网格和Voronoi网格。关于准均匀网格的研究和应用Williamson[14]给出了介绍。图 2给出了几种近年发展且被广泛关注的球面准均匀网格系统。这些网格的划分一般可以帮助有效解决模式积分过程中计算时间步长被少数小格距网格限制过死的问题,同时为模式在更细网格上的应用提供了方便。递减经纬度网格中,网格距的变化仍然较大,因为网格的递减率受到计算方案和极点限制;另外,还要面临纬向计算守恒性的困难。极点的存在,使这一网格还是无法解决矢量场表示的奇异性问题。立方体网格和正二十面体网格则没有上述问题,既克服了极点坐标的奇异性,又容易满足平流计算守恒性,是两个很好的坐标系。美国NOAA GFDL,MIT,海军研究生院、澳大利亚CSIRO、欧洲ECMWF等机构都在使用立方体网格研发模式和算法。但是,在立方体的8个顶点,实际上对应的是8个弱奇异点,计算上仍需留意,只是问题不如常规经纬度坐标严重而已。在立方体网格的6个表面上,矢量场风量 (u,v) 的转换关系也较为复杂,12个棱上的矢量表达更是如此。德国和日本研究机构采用正二十面体的五角形 (最终可分为三角形) 网格建立全球大气模式,其中日本海洋研究开发机构的NICAM模式已经发展成为可以分辨积云的全球动力模式。正二十面体是不规则网格,常规的有限差分算法无法在这里应用,它同样存在弱奇异点。从多尺度计算的观点看,正二十面体网格的嵌套计算非常困难,而渐变网格则又使这种准均匀网格的优点丧失,显然存在一些问题。
|
|
| 图 2. 大气模式中4种较为常用的准均匀网格系统 (a) 递减网格,(b) 正二十面体网格,(c) 立方体网格,(d) 阴阳网格 Fig 2. The fourquasi-uniform spherical grids used for global atmospheric models (a) reducedgrid, (b) icosahydrongrid, (c) cubedgrid, (d) Yin-Yanggrid | |
由图 2d可知,阴阳网格是由阴网格和阳网格两个区域组成的一个球面网格体系,每一个网格区域是常规经纬度网格中的低纬度 (45°S 45°N) 部分,这部分网格的格距变化小,呈准均匀分布,最小与最大格距比为槡2/2。同时,由于只取了常规经纬度网格的低纬部分,自然不包含极点,并远离极区,没有奇异点,经度线随纬度的升高而靠拢的问题并不突出,这对改善计算精度、提高积分运算效率有很好的帮助。还要强调的是,阴阳两个计算区域具有相同的网格结构和格点数,它们相互旋转对称,因此在程序设计上非常简便,可以共用一套源程序计算。那么,只要针对阳网格设计一个区域模式,在阴网格上同时调用这一程序就可以得到全球模式系统,因此可以极其方便地进行全球和区域模式间的转换,实现全球和区域模式通用一个源代码。这样的模式既可以用于全球大气环流计算,又可以用于局地现象的模拟,在粗网格上的细网格嵌套计算和网格自动细化也非常容易,因为所有网格都是规则分布的。这种嵌套不存在模式间的不协调和不平衡,在多尺度计算中表现出很大的优势,因此在通用模式设计中得到重视。
由于阴阳两个区域的存在,使得全球物理量的守恒问题变得突出。事实上,对大气环流模式和气候变化问题而言,计算的守恒性对模式结果和效果非常重要。为此,Peng等[15]针对阴阳网格开发了一个基于有限体积的通量强迫守恒计算方案,有效解决了阴阳网格上采用通量平流方程形式积分的局地和全球守恒问题,在浅水波方程应用中获得了很好的效果。但是,对于平流形式的方程这种方法无法使用,只能通过强迫球面积分总质量、并加以调整分配来实现全球质量守恒的约束。因此,考虑一个全球/区域通用的多尺度数值预报模式应用,应该采用通量形式动力和热力控制方程,同时可以采用有限体积法求解。目前,日本开发的阴阳网格上的大气海洋耦合模式和固体地球动力模式已进入试验应用阶段。对我国多尺度模式GRAPES在阴阳网格上的改进是正在实施的科研任务之一,以获得模式在高纬度地区计算精度和计算效率的改善,并增加模式应用的灵活性。
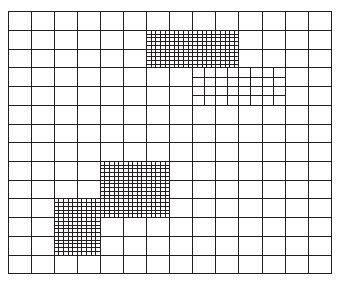
在多尺度计算技术中除了要求网格具有较好的计算动力学特性和较强的格距适应性外,还可以利用双向嵌套计算技术 (图 3) 实现粗细网格的信息交换和相互补充。这种技术早就在中尺度模式中得到广泛应用,但仍然是多尺度预报的一种重要手段。随着计算技术的提高,嵌套网格的边界处理、并行计算问题都得到较好解决,而且可以采用模式变量判断嵌套开始和结束的时间、嵌套的区域,从而实现多个嵌套区域同时计算并分别启动和结束,使模式既可以兼顾分辨率又能节约时间。这样的嵌套技术可以方便地应用于阴阳网格GRAPES模式的改进之中,提高多尺度预报性能和应用灵活性。
|
|
| 图 3. 自动双向嵌套计算 Fig 3. Automatictwo-waynestingtechnology | |
除了水平网格配置和变量分布对多尺度预报/模拟的重要作用之外,垂直坐标的选择和变量配置对模式效果也影响极大。
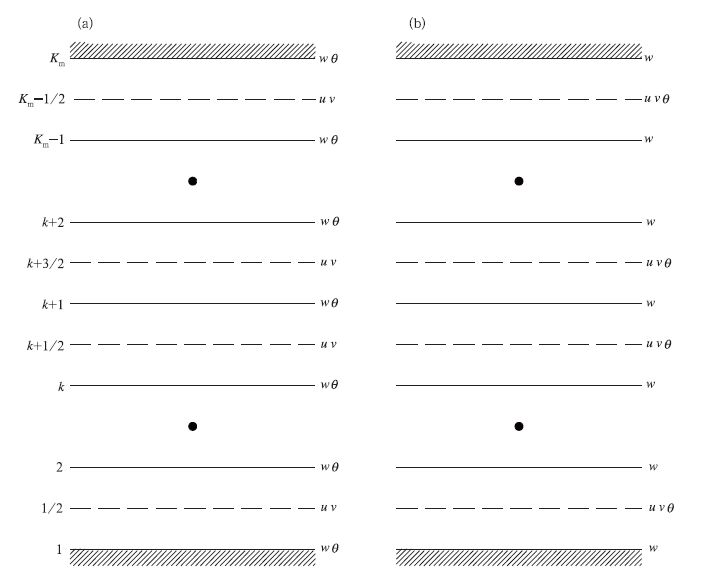
2 垂直坐标和地形处理方案大气的垂直分层结构和斜压性决定了数值模式在垂直方向上也须多层离散化,特别是大气垂直厚度远比其水平尺度小,且垂直方向重力波、声波快波的存在对模式垂直分层有更高要求,模式的垂直分层较水平格距更小,对计算稳定性的要求更高。垂直方向差分运算和计算解的频散关系同样受到变量分布的影响,对模式的总体性能和物理量守恒关系作用极大。Charney-Phillips (CP) 跳点网格是Charney和Phillips[16]1953年提出 (图 4),并成为准地转模式的标准离散方式,因为CP网格上差分方程的准地转位涡守恒非常容易构造。但直到20世纪90年代中期,CP网格在原始方程模式中并没有得到广泛应用。而Lorenz[17]提出的垂直离散法 (LZ网格) 可以构造对非绝热无摩擦过程的能量、平均位温和位温扰动等的守恒格式,从而广泛应用于大气模式。但是,研究发现LZ网格存在虚假计算解[18-19],这是由于采用垂直平均温度和中央差分法计算时两邻层间的气层厚度由它们的平均温度决定的,从而造成了垂直方向温度相对于垂直质量通量自由度的过剩[20],而在CP网格体系中温度和垂直速度具有相同的自由度,不存在这样的计算解。另外,根据Arakawa等[21]的讨论,LZ网格中由于大气斜压不稳定而存在虚假的短波振动,这主要由于位涡在垂直方向上的自由度过剩而产生虚假的斜压不稳定。试验发现,LZ网格不可避免地产生垂直方向温度变量的“之"字振荡,无法正确表现绝热冷却 (或加热) 与温度之间的调整关系,位温扰动的垂直传播被错误“驻留"; 但CP网格正确表达了这一热力学过程,无论对长波和短波过程都能正确反映位温扰动的垂直传播,有利于改善模式对非绝热加热过程的计算效果。
|
|
| 图 4. CP网格配置 (a) 和LZ网格配置 (b) 示意图 Fig 4. IllustrationsofvariablesonCPgrid (a) andLZgrid (b) | |
采用σ坐标系,Arakawa等[22]给出了静力平衡下原始方程模式LZ垂直变量网格分布的计算特性分析比较,指出了CP网格比LZ网格更容易构建能量守恒差分格式。Arakawa等[20]则通过数值试验证明了LZ网格中短波会被放大。当然,考虑大气模式与陆面和海洋模式的耦合,CP网格中温度与水平风的跳层分布使得温度水平湍流计算需采用相应的平均算法,无疑会增加计算误差和计算复杂性;在同样问题上,LZ网格则会增加温度垂直湍流的误差和计算量。总体而言,CP网格对于多尺度模式具有更大的优越性,因为它对虚假小尺度波动和垂直方向的虚假计算解有强的抵抗能力,同时CP网格较LZ网格能更正确地描述波动的垂直传播和绝热加热过程。由于多尺度问题的复杂性和对模式越来越高的要求,许多通用模式开始采用CP网格,如英国气象局UM模式或哈德莱研究中心HadGEM模式、中国气象局GRAPES模式[23-24]等。
另外一个重要问题就是模式的地形处理。在以往计算能力较差、模式分辨率较低的时候,为了方便处理下边界条件普遍采用地形追随 (σ或z*) 坐标,但随着模式分辨率的提高,局地地形的坡度会变得很大,地形追随坐标可以严重破坏三维坐标系的正交性,从而使这一坐标系下的大气动力方程本身出现严重误差[25]。这种坐标系用于多尺度模式构建时,就会在细网格模式或精细预报中产生严重问题。当然,建立数值模式最直接方法就是采用垂直方向高度 (z) 坐标,就不会出现坐标轴正交性被破坏的问题,但这种方法需要面对下垫面地形和下边界条件的处理。
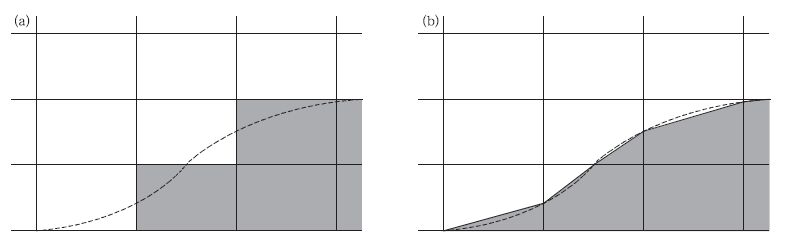
为了简化模式地形处理,Mesinger等[26]设计了一种网格阶梯模式地形处理方法 (Eta模式),后来又被改进为部分网格阶梯地形 (图 5a)。在这种方法中,网格内地形是平坦的,网格间存在地形的不连续变化。阶梯地形虽然对陡地形处理较好,但是这种地形处理在地形比较平滑时会产生对地形重力波的极大歪曲[27]。另一种应用于z坐标系的是线性“切削"地形 (图 5b),这种方法在网格内给出地形的线性垂直廓线来决定地形坡度,使网格内也能表现地形的变化,试验表明这种地形处理对垂直两维非静力模式积分有非常好的动力效果[28],无论对平缓地形还是陡峭地形都可真实反映地形重力波传播。显然,对于多尺度通用模式而言适应性较好的地形处理是不可少的,但这种线性切削地形在三维模式中的应用还有困难,有待进一步开发。
|
|
| 图 5. 网格阶梯地形 (a) 和切削网格地形 (b) 示意图 (虚线为实际地形高度,阴影为模式地形高度) Fig 5. Illustrations of step model topography (a) and shaved-cell topography (b) (dashed line shows true terrain, shaded area shows modal terrain) | |
3 模式动力框架
模式动力框架决定了模式大气的基本动力特性,应用于多尺度通用模式的动力框架首先应该是可以描述各种尺度动力过程、没有假设条件和近似的大气动力学方程组,但是考虑到声波对天气系统发展变化不起作用,可以采用一些近似处理,以滤掉声波。当前世界上最新研究开发的通用模式或多尺度模式大多采用了非静力平衡近似,而且无近似、完全可压缩大气被区域和全球高分辨率模式广泛采用[29]。同时由于计算条件的改善,考虑深厚大气、三维科氏力作用等,甚至有研究开始考虑椭球地球来更加真实地表现地球大气运动。
完全可压缩或半可压缩非静力模式的积分必须考虑声波和重力波的计算。在高空急流之外,声波和重力波往往比风速大数倍,使得积分时间步长受到快波的严格限制。另一方面,由于模式分辨率不断提高,格点模式重新占据主导地位。格点模式的平流和扩散过程可以采用空间差分和时间显式积分方法计算,也可对平流过程采用半拉格朗日法计算,缓解计算稳定性限制,而快波部分的积分可分为3种[29],即完全显式 (AE)、水平显式垂直隐式 (HE-VI) 和全隐式 (HIVI)。在完全显式计算中通常采用时间分离方法分别计算平流和快波过程,而HEVI法则考虑了模式水平和垂直方向尺度的较大差异,而在垂直方向采用隐式计算方法缓解计算稳定性对时间步长的限制。HIVI由于在水平和垂直方向都采用隐式计算方法完全解决了计算稳定性的限制,但是必须以矩阵转换求解Helmholtz方程为代价。
求解Helmholtz过程中不可避免地要进行大量矩阵变形求解,当模式分辨率提高后,使计算量随分辨率呈指数增加,所以许多模式仍采用HEVI进行积分。动力框架的性能关系到整个模式的计算精度和数值解的收敛性,改进和确认多尺度预报模式的动力性能也须对其动力框架进行一系列检验。有关模式动力性能的检验评估问题,历来受到研究开发人员的重视,并开发了相关简化的动力学试验如平流试验、山丘重力波试验、Held-Suarez试验、热泡和冷泡变形运动等。
为解决高分辨率模式求解快波时的困难,近年研究者开始尝试新的求解方法,如特征线法显式求解。根据波流统一的物理概念,运用数学工具将快波传播过程转换成平流运算形式,采用半拉格朗日代替半隐式积分方法计算,不但可以克服计算稳定性的约束,还可以避免求解大型矩阵。Erbes[30]给出了平面直角坐标系中一维浅水波方程重力波的特征线计算和结果,Ogata等[31]得以成功向两维扩展,并获得了较好的计算效果。Peng等[32]则对球面浅水波方程在阴阳网格中实践了重力波的二维特征线算法求解,可以在不涉及矩阵变换的情况下使计算完全稳定,是多尺度模式新型快波计算方法开发的一个有益尝试。
在特征线方法中,最终将重力波传播和风场的平流过程统一,得到在纬向的平流计算方程:
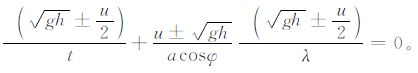
|
(1) |
式 (1) 中,φ,λ分别为纬度和经度,u,h表示纬向风和位势高度。由式 (1) 可看到,重力波传播和平流过程被统一起来,不但是平流的载体,也同时是客体、被输送。与风场不同的是,重力波向正反两个方向传播,所以位势高度场是两个方向波动传播以及风平流结果的叠加。
另外,网格模式的平流过程计算越来越多地选用半拉格朗日方法,这不但因为它可以克服计算稳定性的限制,而且可以保持很好的波动相速和振幅,还可以根据需要构造守恒算法。CIP算法是其中的一种,由于它采用了Hermit插值算法,从而可以在利用相同格点情况下获得更多的次网格信息[33],这在多尺度模式中将表现出更为优越的性质。在GRAPES模式中具有较好性能的Cascade插值法得到应用[34]。
4 模式物理过程物理过程的重要性众所周知,但在以往大气环流模式和分辨率较低的中尺度模式中,由于很多物理过程不可直接分辨而采用参数化的方法在模式中体现。参数化的应用是与模式分辨率息息相关的,随着模式分辨率变化参数选择也应变化,而且在模式分辨率提高到足够高时,原本低分辨模式不可分辨的过程可以被高分辨模式直接分辨,参数化方法必须重新考虑,或者必须改变。基于这一观点,在多尺度模式中需要真实的物理过程计算,开发新的表达方法,兼顾对多种尺度天气过程的影响,才能使之成为通用的模式物理过程。
在这一方面,近年来各种新的、但又是最直接的方法开始在大气模式中应用,如大涡模拟方法、微物理过程直接计算等。这些方法首先考虑了高分辨率情况下的高精度近似,从物理规律本身来描述物理过程变化,一般来说这种描述在高分辨率时较为准确,而低分辨率时则无法正确反映物理过程对模式大气的贡献。另一种是保留参数化并提高参数化的精度或将参数化概念与显式计算方法结合,如高阶湍流闭合方法、超级 (积云对流) 参数化[35]等。
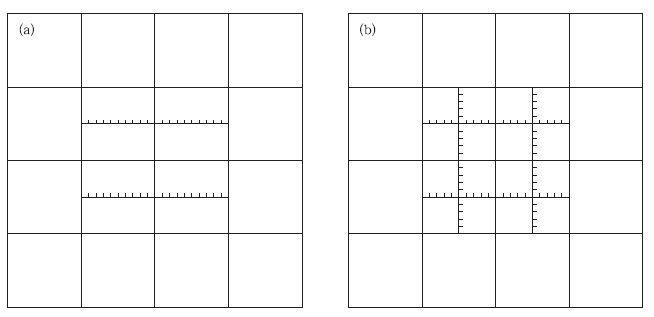
近年来计算能力的快速提高,使微物理过程计算、云谱模式、高阶湍流闭合方案广泛试验并应用于模式,超级参数化方法的实用研究也引起关注。模式垂直扩散的高阶湍流闭合计算也由于计算精度的提高,可以更好地描述层云形成和降水,从而提高模式性能。虽然湍流闭合方案不可避免对湍流项采用参数化,但更高阶的闭合方案可获得更高的计算精度。传统的微物理过程计算和积云对流参数化共存也可以满足对多种分辨率数值预报中水汽循环计算,主要通过开关来人为控制积云对流参数化的有无,在应用于多尺度模拟或通用模式时会出现不同尺度模式间的物理过程不连续。超级参数化则利用云分辨模式计算网格内的对流和热量再分配,有效地将显式微物理过程计算和参数化概念统一起来。具体讲,就是对每一个较粗的模式网格,在某一网格内采用垂直二维或准三维云分辨模式来显式计算次网格水汽循环 (图 6),计算在双向嵌套框架下完成,从而给模式反馈准确的物理量 (水物质和热量) 变化,不存在不同尺度模式间的物理过程不连续问题。采用简单的二维或准三维显式云模式计算网格内次网格过程可以有效节约模式积分时间,又可以提高模式计算效率和计算精度。
|
|
| 图 6. 二维 (a) 和准三维 (b) 云分辨模式进行超级参数化示意图 (小标尺表示云可分辨网格) Fig 6. Two-dimensional (a) and quasi-three-dimensional (b) super parameterization with cloud-resolving model with in acoarse cell (the scale with a cell shows cloud resolving grid size) | |
计算能力的提高可直接在全球模式中采用云分辨模式,比如日本海洋研究开发机构的NICAM模式在7km的分辨率下直接采用详细的微物理过程 (舍弃积云对流参数化) 成功再现了热带对流云团的生命过程,及云团和对流云单体之间的作用关系,并准确描述了云单体和组织性云团相反的运动方向。但必须注意,虽说目前的计算能力达到每秒几百万亿次,但要实现几公里网格上的中长期预报或者气候变化预测还为时过早,寻求一些近似的快捷途径仍然是当前的重要任务。
5 小结和讨论计算条件的改善以及科研和实际预报业务的需要,对多尺度预报和模式开发提出了进一步的要求,大气动力学和计算技术的发展使大家可以选用能够更好保持大气动力学特性的离散化方法、计算方法、以及边界和地形处理等,对大气中复杂物理过程的进一步认识可以在高分辨率模式中选择更直接的计算。以上总结的仅是近年多尺度通用模式新技术发展的部分内容,更多相关的新理论新方法还有待数值预报界的同仁进一步补充和交流。无疑,对于多尺度预报而言,非静力平衡近似既可以满足高分辨率计算,又可以满足低分辩率计算的需要;同样,变量离散化的M网格分布可以同时改进高分辨率和低分辨率模式的频散关系。考虑坐标的正交性,直接采用z垂直坐标对多尺度模式大有裨益,因为高分辨率模式中随着地形坡度的增加地形追随坐标会表现出很大的误差。采用全球和区域通用的动力框架、灵活方便的全球与区域切换开关、以及任意时空点的多重嵌套技术等可以方便多尺度预报的实施,还可以减少模式间的频散适应时间。
由于物理过程的复杂性和认知的局限性,在多尺度预报中采用统一的计算方案确实存在困难。超级参数化是积云对流过程计算一个较好的选择,因为对于任何分辨率的网格都可以细化到云可分辨网格上计算云效果;湍流垂直混合和扩散采用高阶方案或大涡模拟或成为未来的主流,但要求的计算资源非常之大,当今业务预报还难以做到。现有大气环流模式的辐射过程已经较精细,随着多尺度模式中模式分辨率的提高,水汽和云预报精度的提高反过来会提高云长短波辐射的计算。总之,这些方法有的已经成熟应用,有的还在进一步的发展和验证之中,有必要关注和试验,以提高多尺度模式开发、模拟和预报的水平。
对于GRAPES模式的前瞻性研究开发也在科研课题的资助下进行,对非静力平衡模式大气采用阴阳网格、M网格变量分布、三维科氏力计算等方案是改造的重点,构造易于并行运算、(阴/阳、全球/区域) 通用源代码、自由嵌套等多尺度计算技术应用将体现于模式发展之中。关于GRAPES现有多尺度预报技术,读者可参考文献[7-8, 23-24],有助于对模式发展的全面了解。
| [1] | Richardson L F, Weather Prediction by Numerical Process. Lon-don: Cambridge University Press, 1922. |
| [2] | Charney J G, Fiortoft R, von Neumann J, Numerical inte-gration of the barotropic vorticity equation. Tellus, 1950, 2: 237–254. DOI:10.1111/tus.1950.2.issue-4 |
| [3] | 丑纪范, 谢志辉, 王式功. 建立6-15天数值天气预报业务系统的另类途径. 军事气象水文, 2006, 12: 4–9. |
| [4] | 丑纪范. 天气数值预报中使用过去资料的问题. 中国科学a辑, 1974, 17, (6): 635–644. |
| [5] | 邱崇践, 丑纪范. 改进数值天气预报的一个新途径. 中国科学b辑, 1987, 17, (8): 903–910. |
| [6] | Ohfuchi W, Nakamura H, Yoshioka M, 10-km mesh meso-scale resolving simulations of the global atmosphere on the Earth Simulater-Preliminary outcomes of AFES(AGCM for the Earth Simulator). J Earth Simulator, 2004, 1: 5–31. |
| [7] | 张人禾, 沈学顺. 中国国家级新一代业务数值预报系统GRAPES的发展. 科学通报, 2008, 53, (20): 2393–2395. |
| [8] | 陈德辉, 沈学顺. 新-代数值预报系统GRAPES的研究进展. 应用气象学报, 2006, 17, (6): 773–777. |
| [9] | 胡江林, 沈学顺, 张红亮. GRAPES模式动力框架的长期积分特征. 应用气象学报, 2007, 18, (3): 276–284. |
| [10] | Arakawa A, Lamb V R, Computational design of the basic dynamical processes of the UCLA general circulation model. Methods in Computational Physics, 1977, 17: 173–265. |
| [11] | Randall D A, Geostrophic adjustment and the finite-difference shallow-water equations. Monthly Weather Review, 1994, 122: 1371–1377. DOI:10.1175/1520-0493(1994)122<1371:GAATFD>2.0.CO;2 |
| [12] | McGregor J L, Geostrophic adjustment foe reversibly stag-gered grids. Monthly Weather Review, 2005, 133: 1119–1128. DOI:10.1175/MWR2908.1 |
| [13] | Xiao F, Peng X, Shen X, A finite-volume grid using multi-moments for geostrophic adjustment. Monthly Weather Review, 2006, 134: 2515–2526. DOI:10.1175/MWR3197.1 |
| [14] | Williamson D L, The evolution of dynamical cores for global atmospheric models. Journal of the Meteorological Society of Japan, 2007, 85B: 241–269. DOI:10.2151/jmsj.85B.241 |
| [15] | Peng X, Xiao F, Takahashi K, Conservative constraint for a quasi-uniform overset grid on the sphere. Quarterly Journal of the Royal Meteorological Society, 2006, 132: 979–996. DOI:10.1256/qj.05.18 |
| [16] | Chaney J G, Phillips N A, Numerical integration of the qua-si-geostrophic equations for barotropic and simple baroclinic flows. Journal of Meteorology, 1953, 10: 71–99. DOI:10.1175/1520-0469(1953)010<0071:NIOTQG>2.0.CO;2 |
| [17] | Lorenz E N, Energy and numerical weather prediction. Tel-lus, 1960, 12: 364–373. |
| [18] | Tokioka T, Some consideration on vertical differencing. Journal of the Meteorological Society of Japan, 1978, 56: 89–111. |
| [19] | Hollingsworth A, A Spurious Mode in"Lorenz" Arrangement of Φ and T Which Does not Exist in the"Charney-Phillips"Ar-rangement. ECMWF Tech Memo, 1995, 211: 1–12. |
| [20] | Arakawa A, Konor C S, Vertical differencing of the primitive equations based on the Charney-Phillips grid in hybrid σp vertical conrdinates. Monthly Weather Review, 1996. |
| [21] | Arakawa A, Moorthi S Baroclinic instability in vertically discrete system. Journal of the Atmospheric Sciences, 1996, 124: 511–528. |
| [22] | Arakawa A, Suarez M J, Vertical differencing of the primi-tive equations in Sigma coordinates. Monthly Weather Review, 1983, 111: 34–45. DOI:10.1175/1520-0493(1983)111<0034:VDOTPE>2.0.CO;2 |
| [23] | 陈德辉, 杨学胜, 张红亮. 多尺度非静力通用模式框架的设计策略. 应用气象学报, 2003, 14, (4): 452–461. |
| [24] | 薛纪善, 陈德辉. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 2008: 1-383. |
| [25] | Thompson J F, Warsi Z, Mastin C, Numerical Grid Genera-tion:Foundations and Applications. North-Holland:Elsevier Science Publishing Company, 1985. |
| [26] | Mesinger F, Janjic Z, Nickovic S, The step-mountain coordinate:Model description and performance for cases al-pine lee cyciogenesis and foe a case of an Appalachian redevel-opment. Monthly Weather Review, 1988, 116: 1493–1518. DOI:10.1175/1520-0493(1988)116<1493:TSMCMD>2.0.CO;2 |
| [27] | Gallus W, Klemp J, Behavior of flow over step orography. Monthly Weather Review, 2000, 128: 1153–1164. DOI:10.1175/1520-0493(2000)128<1153:BOFOSO>2.0.CO;2 |
| [28] | Yamazaki H, Satomura T, Vertically combined shaved cell method in a z-coordinate nonhydrostatic atmospheric model. Atmospheric Science Letters, 2008. DOI:10.1002/asl.187 |
| [29] | Saito K, Ishida J, Aranami K, Nonhydrostatic atmos-pheric models and operational development at JMA. J Meteo-ro Soc Japan, 2007, 85, (85B): 271–304. |
| [30] | Erbes G, A, semi-Lagrangian method of Characteristics for the shallow-water equations. Monthly Weather Review, 1993, 121: 3443–3452. DOI:10.1175/1520-0493(1993)121<3443:ASLMOC>2.0.CO;2 |
| [31] | Ogata Y, Yabe T, Multi-dimensional semi-Lagrangian char-acteristic approach to the shallow water equations by CIP method. International J Comput Eng Sci, 2004, 5: 699–730. DOI:10.1142/S1465876304002642 |
| [32] | Peng X, Chang Y, Li X, Application of the character-istic CIP method to shallow water model on sphere. Adv At-mos Sci, 2010, 27. DOI:10.1007/s00376-009-9148-6 |
| [33] | Yabe T, Tanaka R, Nakamura T, An exactly conser-vative semi-Lagrangian scheme(CIP-CSL)in one dimension. Mon Wea Rea, 2001, 129: 332–344. DOI:10.1175/1520-0493(2001)129<0332:AECSLS>2.0.CO;2 |
| [34] | 陈峰峰, 王光辉, 沈学顺. Cascade插值方法在GRAPES 模式中的应用. 应用气象学报, 2009, 20, (2): 164–170. |
| [35] | Randall D, Khairoutdinov M, Arakawa A, Breaking the cloud parameterization deadlock. Bull Amer Metero Soc, 2003, 84: 1547–1564. DOI:10.1175/BAMS-84-11-1547 |
 2010, 21 (2): 129-138
2010, 21 (2): 129-138

