应用气象学报  2010, 21 (1): 83-88   PDF    
引用本文
赵南, 甘璐, 沈新勇. 涡旋流自发辐射惯性重力波的初步解析研究[J]. 应用气象学报, 2010, 21(1): 83-88.
Zhao Nan, Gan Lu, Shen Xinyong. A Preliminary Analytical Study on the Spontaneous Emission of Inertia gravity Waves from Vortical Flows[J]. Journal of Applied Meteorological Science, 2010, 21(1): 83-88  
涡旋流自发辐射惯性重力波的初步解析研究
赵南1,2, 甘璐1, 沈新勇2,3     
1. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081;
2. 南京信息工程大学气象灾害省部共建教育部重点实验室, 南京 210044;
3. 马里兰大学大气海洋科学系, 马里兰 20742, 美国
2009-04-14 收到, 2009-10-19 收到修改稿.
资助项目: 灾害天气国家重点实验室科研业务费、国家自然科学基金项目（40775033）、公益性行业科研专项经费项目（GYHY200806009）、国家重点基础研究发展规划项目（2009CB421503，2004CB418301）及江苏省青蓝工程（2009）共同资助    
摘要: 平衡流（或粗略地说涡旋流）调整目前被认为是惯性重力波产生的一种新的机制并被称为自发辐射问题。基于f平面上正压模式，该文对涡旋流自发辐射惯性重力波这一问题进行了初步解析研究。首先，通过该模式讨论了慢流形和平衡流的概念并强调了平衡流的涡旋运动特征。假定Froude数F＜＜1且Rossby数ε=O（1）（即近似为平衡流的涡旋流包括了梯度风和其他非地转成分），于是基本方程可以写为有关惯性重力波的非齐次波动方程，其非齐次项与涡旋流的非平衡性质有关，而对于严格平衡的涡旋流，非齐次项消失, 故涡旋流的非平衡性实际上提供了惯性重力波的强迫源, 通过找出该方程的格林函数给出了反映自发辐射的非齐次解。在远离波源的区域，该非齐次解可以展开为远场形式，包括单极、偶极和四极辐射, 另一方面，在波源区域以内及其附近，解的近场形式可以看作是慢流形的近似表达式。结果表明：与涡旋流相伴随的辐合/辐散运动主要由两部分组成，即由它自发辐射出的惯性重力波以及从属于平衡流的缓慢变化的辐合/辐散运动。与Ford的匹配渐近展开方法相比较，尽管不能给出更高阶近似，但格林函数法得到的非齐次解形式，在描写自发辐射方面更具物理直观性。
关键词: 平衡流    慢流形    惯性重力波    自发辐射    解析研究    
A Preliminary Analytical Study on the Spontaneous Emission of Inertia gravity Waves from Vortical Flows
Zhao Nan1,2, Gan Lu1, Shen Xinyong2,3     
1. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
2. Key Laboratory of Meteorological Disaster of Ministry of Ed ucation, Nanj ing University of In formation Science & Technology, Nanj ing 210044;
3. Department of Atmospheric and Oceanic Science, University of Mary land, College Park, Mary land 20742, US A
Abstract: The emission of inertia gravity waves from the adjustment of balanced flows (or, basically, vortical flows) is currently regarded as a new mechanism of the pro duction of inertia gravity waves and referred as the spontaneous emission. Base d on f plane barotropic model, a preliminary analytical study on the spontaneou s emission of inertia gravity waves from vortical flows is conducted. First of all, the concept of slow manifold and balanced flow are discussed via this model and vortical property of the balanced flow is emphasized. Then, by assuming tha t the Froude number F and Rossby number satisfy and (implying that vortic al flow approximately balanced flow that includes gradient wind and other ageost rophic contributions), the basic equations are simplified to an inhomogeneous wa ve equation of inertia gravity wave, while the inhomogeneous term is related to the imbalance of the vortical flow. This inhomogeneous term vanishes when vorti cal flow is exactly balanced. So the imbalance of the vortical flow provides a f orcing or source to the inertia gravity wave. The Green function of this equa tion is found to give the inhomogeneous solution standing for the spontaneous em ission. In the field far from the wave "source", this inhomogeneous solution c an be expanded into far field form, including wave emission of monopole, dipole and quadrupole types. On the other hand, within or near to the "source" field, the near field form can serve as an approximate expression of the slow manifo ld. These results indicate that the convergence/divergence fields accompanied wi th vortical flows is composed of two main parts, i.e., the spontaneous emission o f inertia gravity waves from vortical flows and slow varying convergence/diver gence filed slaved to the adjustment of balanced flow. Although higher order ap proximation solution has already been given by Ford (2000) using method of match ed asymptotic expansions, the Green function solution can depict the spontaneo us emission in a more physical way.
Key words: balanced flow     slow manifold     inertia gravity wave     spontaneous emission     analy tical study    
引言

在中高纬度地区，气象学上有意义的波动主要包括惯性重力波和Rossby波.从波的物理性质来说，惯性重力波的存在与稳定的大气层结下的浮力振荡及科氏力有密切关系，而惯性重力波以外的其他波动则主要依赖于大气运动的地转平衡.另外，从波的时间尺度运动学特征而言，前者为较快且与辐散、辐合运动相关；而后者相对较慢并与涡旋运动相关联.尽管主要的天气、气候现象与Rossby波的活动直接相关，近年来研究表明，惯性重力波引起的垂直动量输送在维持中层大气的环流及其变率中扮演着重要角色[1-2]，同时惯性重力波也可以触发对流活动，因而最终会对天气、气候产生影响.这使得人们开始重视对惯性重力波的研究.众所周知，惯性重力波产生的主要来源除了地形强迫、Kelvin-Helmholtz切变不稳定和对流不稳定等行为对稳定层结大气的冲击之外[3-5]，人们也已经认识到地转调整过程伴随着惯性重力波.近年来，随着慢流形、平衡流及PV反演等一些基本理论问题研究的进展[6-15]，人们对于上述最后一种惯性重力波的产生机理有了更加深刻而全面的认识，即提出并研究了一般的平衡流调整过程中释放惯性重力波的问题，并将其看作是一种惯性重力波产生的新机制.在这一机制中所谓的平衡流是一个基础性概念.在研究大气运动时通常习惯于将其划分为波和流两种形态，前者的主要特征是具有在大气中传播的性质，而后者具有相对稳定少变的性质.有关波与流的区分方法通常依据所研究的问题不同有所差异，因而没有统一的划分方法.在侧重研究惯性重力波的激发与作用时，可以将除去惯性重力波后的部分称为流.由于这种流是一种相对缓慢调整且满足某种平衡关系的运动，通常称其为平衡流，显然Ross-by波也被包含在其中.但平衡流远非仅仅由这些以及其他准地转运动模态构成，其内涵远比单纯的地转平衡更为丰富.本文将从平衡流与惯性重力波相互关系角度，解析地分析平衡流释放惯性重力波问题.

1 平衡流与涡旋流

首先，需要通过适当方式给出平衡流的准确定义.由此引出了一系列理论问题的研究 (详细讨论见文献[6]).为了叙述方便，以下以f平面上正压模式为例进行说明.将其散度、涡度和连续方程写为

(1)
(2)
(3)

其中，u=curl-1 ζ+div-1 δ，H为流体静态厚度，F，G为某种泛函.其他符号都取其通常的意义.为了区分惯性重力波和所谓的平衡流，需要注意主要由散度δ描述的惯性重力波相对于主要由涡度ζ描述的平衡流是一种快过程，而后者是一种慢过程.这两种过程通过控制方程式 (1)~(3) 复杂地耦合在一起，因此如果严格定义平衡流必须设法在式 (1)~(3) 中将两种过程的描述分离开来.通常这种解耦的可能性是有条件的，并限于某种特定运动形态.一般地，如果快变量δ与慢变量ζ间存在某种 (泛函) 关系

(4)

将式 (4) 代入式 (1)，并在时间偏导中引入式 (2) 和式 (3) 右端后，使得

(5)

成立，则此时式 (1)~(3) 退化为

(6)
(7)

式 (6)~(7) 所描述的是不包括惯性重力波的有旋运动，称之为慢流形式 (4) 上的平衡运动.而称式 (5) 为 (超) 平衡方程.将关系式 (4) 在 (δ，ζ，φ) 所张成的相态空间中对应的广义曲面称为慢流形 (slow manmanifold)，它是动力学系统式 (1)~(3) 的所谓不变流形，换句话说，一旦相态位于其上则其运动将永远被限制在它上面而不能逸出.将满足上述性质的大气运动定义为平衡流.显然，平衡流的存在依赖于慢流形的存在，而后者原则上需要通过求解超平衡方程 (最一般情况是泛函方程) 来确定.

作为式 (4) 的特殊情况，慢流形的另一种更为常见的定义方式为

(8)

即平衡流为不包括辐合、辐散的涡旋运动.此时式 (5) 变为

(9)

称式 (9) 为平衡方程.从平衡方程各项构成来看，这里所指的平衡流本质上反映了不包括惯性重力波贡献的惯性力、科氏力和气压梯度力之间的某种平衡关系.因此原则上它可以是各种尺度上的平衡关系 (准地转平衡仅仅是大尺度情形下的近似)，它可以是梯度风平衡甚至是中小尺度的涡动.其共同特征与大气涡旋运动分量有关.从这点来看，所谓平衡流并不限于大尺度的准地转平衡.

理论分析表明，除了一些特殊情况如满足地转平衡的平行流及轴对称同心流之外，严格满足上述定义的平衡流是不存在的[9，11-12].但在模糊慢流形的概念下[12]，它仍然是一个很好的近似概念.由于这样定义的平衡流以涡旋运动为其主要特征，作为近似概念称其为涡旋流.

2 自发辐射的解析解及其性质 2.1 自发辐射

可以证明由式 (1)~(3) 有

(10)

这里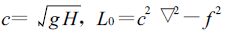为Helmhol tz算子.可以看出，式 (10) 左端为线性惯性重力波算子∂2/∂t2-L0作用于散度场δ，而方程的右端由非线性项组成.惯性重力波自发辐射 (Lig thill[16]，Ford等[12]) 的核心思想是方程右端的主要贡献在Froude数F=U/c＜＜1时，可以近似认为主要来自非定常的涡旋运动.因此，它可以看作是某种给定惯性重力波的“波源”.与由某种外在的初始扰动所导致的自由惯性重力波比较而言，它被视为由涡旋流自发产生的惯性重力波，故称波自发辐射.事实上，当Froude数F＜＜1且Rossby数ε=0(1)，即中小尺度缓慢流速运动时可以证明

(11)

证明中散度量纲由连续方程式 (3) 的线性部分可知，有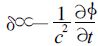.若考虑其中的时间尺度为1/ f，同时在式 (1) 中假定气压梯度力与惯性离心力相同量级，得到的量级为U2，则δ的量级为fF2.而涡度的量级可以直接由速度和空间尺度的量级估出即有ζ∝U/L，考虑到Rossby数ε=U/ f L，可以得到式 (11).此时有

(12)

故式 (10) 可以写为

(13)

其中

(14)

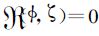
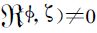
与δ无关，可以视为涡旋流对惯性重力波的外源强迫.容易证明在式 (8) 或式 (9) 所给出的平衡流条件能够严格满足的情况下.但是除了一些非常特殊的情况 (通常是一些对称流) 下，平衡流条件不能严格满足，而与这种严格平衡流的偏离密切相关，正是这种偏离是惯性重力波强迫源.由该“波源”向外放射惯性重力波的物理图像可以作如下理解:假定涡旋流被限制在一个有限的区域内 (图 1，阴影区)，该区域可以视为“波源”区，其中任意一点为r′，则远离该区域的r处可以观测到由“波源”区放射出来的纯粹的惯性重力波.

图 1. 被限制在一个有限的区域内 (阴影区D) 的涡旋流自发辐射惯性重力波示意图 Fig 1. The sketch map of spontaneousemission of inertia-g ravity waves fromvertical flow confined to afiniteregion (shadow part D)

2.2 解析解

当用式 (13) 描述自发辐射时，可以通过格林函数得到其精确解.设G为其格林函数，则有

(15)

对式 (15) 进行时间变量的傅氏变换有

(16)

其中G是G的傅氏变换.由Helmholtz方程的格林函数[17]可得

(17)

这里H0(1)为Hankel函数.式 (17) 的傅氏逆变换F-1给出格林函数

(18)

其中，用到了以下公式[18]

(19)
(20)

于是式 (13) 的解为

(21)

这里Ψ代表r-r′＜c(t-t′) 的积分区域，并且已考虑r-r′ >c(t-t′) 区域的格林函数为纯虚数，对散度场无贡献.任意时刻t在r处的惯性重力波的振幅由较早所有时刻t′各个r′处强迫效应的累计决定.若将r-r′=c(t-t′) 视为纯粹的重力波的波阵面，则式 (21) 显示，这种影响与r距波阵面的距离成反比，且波阵面过该点之后的影响以惯性振荡为主，而波阵面过该点之前则无影响.总之，惯性重力波主要表现为纯粹的重力波波阵面附近的扰动.图 2给出反映格林函数时空结构的等值线图，上述主要特征得到清楚反映.

图 2. 反映格林函数时空结构的等值线图 (已经进行了无量纲化，仅在负位相区域 (阴影区) 画出等值线0.000，-0.025，-0.050，-0.075，-0.125，-0.20，-0.30，-0.40，-0.50) Fig 2. The contour map of the non-dimensio nalizedspatio-tem poral struc ture of the Green function (contour lines are drawn only in the negative phase (shadows) at 0.000, -0.025, -0.050, -0.075, -0.125, -0.20, -0.30, -0.40, -0.50)

2.3 远场近似---多极辐射

若涡旋流的空间尺度为L，流速的尺度为U，则由它辐射出的惯性重力波的特征频率为U/L.由惯性重力波的频散关系及F=U/c，可得惯性重力波的特征波长≥2πL/F，由此可以看出在描述波动性质时通常应当考虑

(22)

即惯性重力波的特征尺度远大于涡旋流的尺度.此时式 (21) 可以在r′=0附近展开得到，

(23)

这里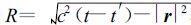，且

(24)
(25)
(26)

这里D代表涡旋流集中的区域，考虑Rossby数ε=O(1) 的情形，该区域比较集中.而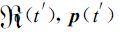和q(t′) 分别为标量、向量和张量.它们分别为单极子、偶极子和四极子，取决于涡旋场的分布.Ford等[12]使用远场和近场渐进匹配摄动法的分析结果指出对于Froude数F＜＜1的情形下，自发辐射以四极辐射为主.

2.4 近场近似---慢流形的表达

另一方面当以式 (4) 作为慢流形的一般定义时，式 (13) 可以用作寻找这种慢流形的具体表达.一般地，可以将其解看作包括惯性重力波在内的模糊慢流形的表达.如果在其中滤去惯性重力波，其余部分即可认为是慢流形.可以证明，在涡旋流区域D内惯性重力波算子∂2 /∂t2-L0中有

(27)

式 (27) 中，“ ≈”是因为在F＜＜1且Rossby数ε=O(1) 的情况下，有c2/L2=(ε/F)2 f2＞＞f 2.如果强制∂2 /∂t2=0，于是

(28)

为Helmholtz方程，通过格林函数法可以求解出近似慢流形表达式

(29)

其中，K0为零阶MacDonald函数[19]

(30)

比较式 (21) 和式 (29) 可知，与涡旋流伴随的辐合辐散可以有两部分组成:①惯性重力波的辐合辐散，它是相对快变的振荡/传播运动；②从属于平衡流的辐合辐散，是相对缓慢的调整.

3 小结和讨论

本文从f平面正压模式出发，解析地研究了涡旋流或平衡流通过自发辐射产生惯性重力波的问题.首先通过格林函数给出了涡旋流自发辐射惯性重力波的解析解，在此基础上通过其远场近似研究了自发辐射的具体形式即多极辐射问题，并且通过涡旋流近场近似给出了刻画其平衡流性质的慢流形的表达式.据此可将辐合辐散运动分为两部分:从属于平衡流的散度场以及由平衡流自发辐射出的惯性重力波.

在上述讨论中，散度场远弱于涡度场是自发辐射占主导地位的前提条件.然而对于严格成立的平衡流如满足地转平衡的平行流及轴对称同心流的特殊情况下有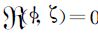，即不存在自发辐射源.此时式 (10) 右端不能忽略散度的贡献，而惯性重力波的产生则主要是来源于平衡流的切变不稳定，如惯性不稳定和Kelvin-Helmholtz不稳定 (层结大气情形).这种情况下，以稳定性问题为主.在一般情况下，严格的平衡流不能存在，而作为近似概念的平衡流并不构成原始方程的解，也就无从提出稳定性问题，此时只有自发辐射问题.需要指出这两类问题的区别是，前者需要外在的初始扰动，后者由涡旋流自发产生.

参考文献
[1] Dunkerton T J, The role of gravity waves in the quasi-biennial oscillation. Journal of Geophysical Research, 1997, 102: 26053–26076. DOI:10.1029/96JD02999
[2] Holton J R, Role of gravity-wave-induced drag and diffusion in the momentum budget of the mesosphere. Journal of the Atmospheric Sciences, 1982, 39: 791–799. DOI:10.1175/1520-0469(1982)039<0791:TROGWI>2.0.CO;2
[3] 王晓芳, 崔春光, 胡伯戚. 与水平风切变强度不均匀相联系的CISK惯性重力波. 应用气象学报, 2007, 18, (6): 760–768.
[4] 吴洪, 林锦瑞. 垂直切变基流中东西向地形对惯性重力波稳定性的影响. 应用气象学报, 1997, 8, (2): 242–246.
[5] 王永中, 夏友龙. CISK影响下的线性和非线性惯性重力波. 应用气象学报, 1996, 7, (1): 82–88.
[6] 赵南, 沈新勇, 丁一汇. 大气运动的慢流形概论. 地球科学进展, 2007, 22, (4): 331–340.
[7] Lorenz E N, Attractor sets and quasi-geostrophic equilibrium. Journal of the Atmospheric Sciences, 1980, 37: 1685–1699. DOI:10.1175/1520-0469(1980)037<1685:ASAQGE>2.0.CO;2
[8] Lorenz E N, On the existence of a slow manifold. Journal of the Atmospheric Sciences, 1986, 43: 1547–1557. DOI:10.1175/1520-0469(1986)043<1547:OTEOAS>2.0.CO;2
[9] Lorenz E N, Krishnamurthy V, On the nonexistence of a slow manifold. Journal of the Atmospheric Sciences, 1987, 44: 2940–2950. DOI:10.1175/1520-0469(1987)044<2940:OTNOAS>2.0.CO;2
[10] Vautard R, Legras B, Invariant manifolds, quasi-geostrophy and initialization. Journal of the Atmospheric Sciences, 1986, 43: 565–584. DOI:10.1175/1520-0469(1986)043<0565:IMQGAI>2.0.CO;2
[11] Lorenz E N, The slow manifold-Whet is it. Journal of the Atmospheric Sciences, 1992, 49: 2449–2451. DOI:10.1175/1520-0469(1992)049<2449:TSMII>2.0.CO;2
[12] Ford R, McIntyre M E, Norton W A, Balance and the slow quasimanifold:Some explicit results. Journal of the Atmospheric Sciences, 2000, 57: 1236–1254. DOI:10.1175/1520-0469(2000)057<1236:BATSQS>2.0.CO;2
[13] McIntyre M E, Balance.Potential-vorticity Inversion, Lighhill Radiation, and the Slow Quasimanifold∥Proc IUTAM/IUGG/ Royal I rish Academy Symposium on Ad vanced in Math ematical Modelling of Atmos phere and Ocean.Ireland, 2000.
[14] Warn T, Bokhove O, Shepherd T G, et al. Rossby number expansions, slaving principles, and balance dynamics, Quarterly. Journal of the Royal Meteorological Society, 1995, 121: 723–739. DOI:10.1002/(ISSN)1477-870X
[15] Vallis G K, Potential vorticity and balanced equation of motion for rotating and stratified flows. Quarterly Journal of the Royal Meteorological Society, 1996, 122: 291–322. DOI:10.1002/(ISSN)1477-870X
[16] Lighthill M J.On Sound Generated Aerodynamically, I:General Theory∥Proceedings of the Royal Society of London.1952, A211 :564-587.
[17] 郭敦仁. 数学物理方法. 北京: 人民教育出版社, 1979.
[18] 路季平. 积分变换及在物理海洋学中的应用. 北京: 海洋出版社, 1984.
[19] 刘式适, 刘式达. 特殊函数. 北京: 气象出版社, 1988.