2. 国家气象中心, 北京 100081;
3. 北京市观象台, 北京 100089
2. National Meteorological Center, Beijing 100081;
3. Beijing Weather Observatory, Beijing 100089
浙江省地处亚热带, 有着绵长曲折的海岸线, 受太平洋西行台风的影响, 近年来, 人口密度不断加大, 台风灾害影响越来越引人关注[1-3], 一个客观、科学的灾害影响评估方法将有助于防灾减灾工作的有效开展。目前, 国内很多学者对此做了相关研究。李春梅等[4]将层次分析法和专家打分法应用于广东省热带气旋灾害影响评估模式中; 卢峰本等[5]利用逐步回归方法对防城港市的热带气旋造成的灾情进行了定量评估研究; 樊琦等[6-7]基于模糊数学方法提出了灾害评估模型。这些研究多数考虑了台风的风、雨等因素, 但较少考虑承灾体的影响时间、天文大潮等因子, 且具体到浙江省的研究更少。本文在利用模糊数学方法建立模型的基础上, 加入台风影响时间、致灾因子、孕灾环境等10个因子, 对灾情进行定量评估, 并采用冯利华[8]提出的灾级概念得到实际灾情灾级指数, 用以检验模型效果, 取得了较为理想的结果。模型中, 只要获得台风预测资料及影响地区经济社会信息, 即可进行灾前预评估、灾中和灾后的快速评估, 从而为政府及相关部门应急决策管理提供参考依据。
1 资料和因子选取 1.1 资料来源热带气旋资料取自《热带气旋年鉴》[9], 人口、耕地面积和国内生产总值均取自于《浙江统计年鉴》[10], 热带气旋造成的损失资料来源于国家气象中心的统计数据。考虑到社会经济发展, 取经济与当前较接近的2000-2006年资料进行分析。在21个影响浙江省的热带气旋中选取20个, 剔除1个灾情资料无法获全的台风。
1.2 因子选取 1.2.1 评价指数的因子选取台风灾害的主要类型有暴雨灾害、狂风灾害、风暴潮灾害等。重大热带气旋灾害多数是由其带来的狂风、暴雨和大海潮的共同影响以及其灾害链所形成的[11-12]。因此, 选用热带气旋影响到浙江时的最低气压、最大风速、天文大潮指数以及24 h和过程降水量极值、持续时间、范围作为评价指数的关键因子。此外, 由于浙江各地区的经济发展不平衡, 人口密度也相差较大, 同一台风在不同地区造成的灾害也不同, 所以模型也考虑了影响区域人口、耕地面积以及GDP。这样, 共选取10个因子放入模型中进行计算:A1为过程最大降水量, A2为24 h最大降水量, A3为浙江最大风速, A4为浙江最低气压, A5为影响持续时间, A6为影响范围(50 mm以上降水和6级以上大风影响的站点), A7为影响区域GDP, A8为影响区域的人口, A9为影响区域耕地面积, A10为登陆时的天文大潮指数。
1.2.2 灾级指数的因子选取热带气旋灾害不论是成因还是形式都是复杂多样的, 但它所造成的社会损失最终可以归结为人员伤亡和财产损失两个方面[13]。在人员伤亡中, 死亡是一种重大损失, 但是受伤也不容忽视。而财产损失则包括直接经济损失和间接经济损失两个部分, 由于间接经济损失难以计算, 故一般只考虑直接经济损失。这样, 在灾级指数计算中本文考虑死亡人数、受伤人数和直接经济损失3个因子。
1.3 资料处理影响区域GDP为浙江省各市GDP乘以影响各市范围的比例累加所得; 影响区域人口以及耕地面积为全省人口和耕地乘以影响范围的比例所得; 天文大潮在登陆时遇农历初一、初二、初三或十五、十六、十七时考虑, 否则不考虑; 过程最大降水量、24 h最大降水量、最大风速均直接使用观测或预报值; 持续时间为台风影响浙江的时间; 影响范围以站为单位。
2 评价模型的建立 2.1 隶属函数的确定模糊数学是一门研究模糊性现象的数学, 而现代数学和集合论是密切相关的, 因此模糊集也就用来研究模糊现象, 常用隶属函数来刻画, 以实现定量描述模糊性事物[14-15]。隶属函数的确定在一定程度上具有主观性和经验性, 确定方法一般有模糊统计法、典型函数法等。本模型中采用典型函数法的戒下型函数[16-17], 表达式如下:
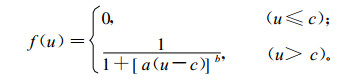
|
(1) |
式(1) 中, f (u) 为因子u的隶属函数; a, b, c均为参数, 且a > 0, b < 0, c > 0。
戒下型函数的分布, 可以表示台风灾害轻重程度。当因子u的值大于某一界值c (因子u历年统计值的最小值) 时, 认为可以成灾, 否则不成灾。规定b=-2;c=umin; 令u的历年统计最大值为umax, 所对应隶属函数的值为0.99, 这样通过式(1) 可得a值。另外, 在计算时a值偏大, 因此定义一个经验系数K, 使a值能够有利于隶属度的计算:
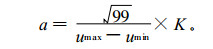
|
(2) |
经多次试验计算, 取K为0.3较为合适。
2.2 评价矩阵的确定设有n个台风等待评价, m个影响因子来进行评价, 则每个因子的评价集为Ri=(ri1, ri2, …, rin), i=1, 2, …m, 从而可以得到m个影响因子评价矩阵R, 矩阵中的每1个元素都是通过隶属度公式(式(1)) 计算得到的, 因此当a, b, c确定后, 便可以求出每个台风的各灾情因子隶属度值, 这样, 总的评价矩阵可以表示为:
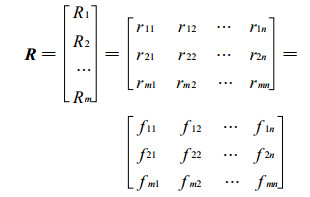
|
(3) |
模型中权重系数的大小反映了各参评因子的相对重要程度, 因子取值将直接影响到评价结果。常用的定权方法有:专家咨询法、调查统计法等, 但这些方法过多依赖于人的主观经验和难以收集的统计数据。因此, 为客观、准确地确定权重值, 李登峰等[18]利用加权平均规划法得到的权重计算在实际应用中效果较好。此方法首先建立多目标决策模型:
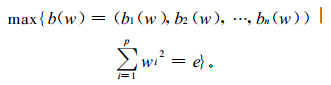
|
(4) |
式 (4) 中, 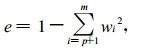
由于本文中的影响因子权重均未知, 所以p=m, d=1(待定因子的权重之和为1)。
将上述多目标决策问题等权重集结为等价的非线性规划问题, 最终解得权重表达式为
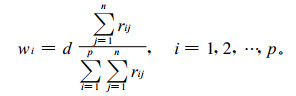
|
(5) |
利用权重计算式, 即式(5)可得各影响因子的权重分配, 见表 1。
|
|
表 1 各因子权重分配 Table 1 Weighting of various factors allocation |
由表 1可见, 通过加权平均规划法得到的各因子权重基本反映了其对综合评价指数的贡献。其中, 最低气压、最大风速、过程最大降水量3个因子的贡献力度最大, 影响持续时间、影响范围因子次之, 紧接着后面依次是影响区域GDP, 24 h最大降水量、登陆时天文大潮指数、影响区域耕地面积和人口因子。可以看出, 模型除了24 h最大降水量因子以外, 大体上都将自然灾变因素放在了首位, 其次是经济因素和社会因素, 这与台风致灾原因、过程等理论知识和实际经验基本一致, 表明此方法所得的权重分配是合理的。
2.4 综合评价指数的计算方法在确定了评价矩阵R和因子权重集W后, 即可从模糊变换原理得到综合评价指数集B:
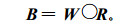
|
(6) |
B就是n件事物的模糊综合评价指数集, 指数越大表示灾害程度越严重。在这里, “ ○ ”为广义模糊算子, 其算法有多种模型, 这里采用加权平均型模型, 即
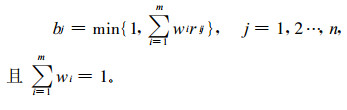
|
(7) |
本文引用文献[8]提出的灾级概念, 计算了台风灾害的灾级指数。方法如下:首先将死亡人数(s)、受伤人数(h)、直接经济损失(q)3个因子换算成规范化指数, 即当s≥100人, h≥1000人, q≥1000万元时, 利用对数函数换算成规范化指数, 其表达式为
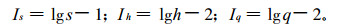
|
当s < 100人, h < 1000人, q < 1000万时, 则利用线性函数换算成规范化指数, 表达式为
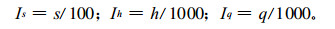
|
计算灾级指数G, 即
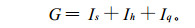
|
(8) |
该指标G具体反映了现实灾情的大小, 所以用来检验评价模型的评估效果。
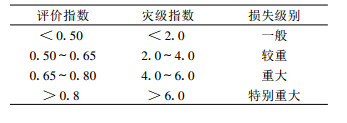
4 台风灾害的综合模糊评价 4.1 评价指数和灾级指数的计算及分级考虑到模型要在将来工作中应用, 资料的选取应尽量与当前社会环境接近。因此, 选取2000-2006年影响浙江省的20个台风, 计算各个例的评价指数和灾级指数。由于评价指数是根据评估模型和灾害影响关键因子计算出来的, 所以可以预测灾情的大小, 而灾级指数是根据灾后实际灾情资料计算出来的, 客观地反应受灾情况。为了确定评估效果, 将评价指数和灾级指数均分成4个等级, 各级域值如表 2所示。
|
|
表 2 灾害损失、灾级指数与评价指数分级 Table 2 The classification of every disaster grade, loss and evaluation index |
4.2 评估结果分析
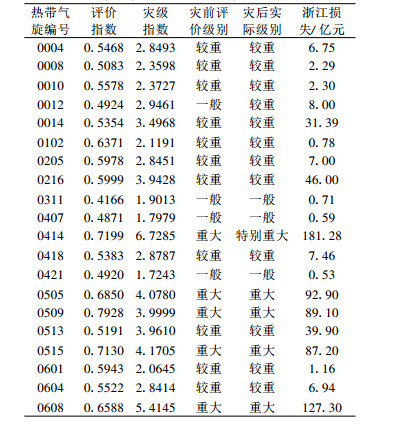
利用上述等级域值将20个台风两指数分别划定其所属级别并列于表 3中, 对比灾前评价级别和灾后实际级别可以看出, 模型全部个例两指数同级的一致率达到了90 %, 且错报等级也仅差一级。仅在0012号、0414号台风评估偏轻, 其中0414号台风造成的受伤人数过大, 达数千人, 这种人为因素和偶然因素的综合影响, 是目前评估技术所不能达到的, 所以评估级别稍轻。
|
|
表 3 2000-2006年影响浙江省的台风个例评价指数与灾级指数的对比分析 Table 3 The comparison of disaster grade and evaluation index of every tropical cyclone influence on Zhejiang Province during 2000-2006 |
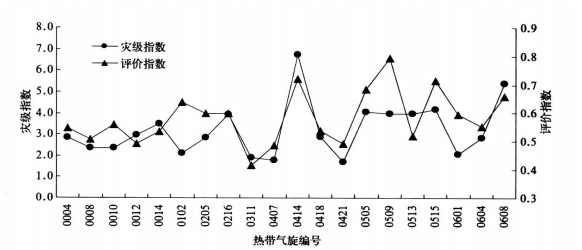
另外, 在这20个台风中, 评价指数和灾级指数的对应关系也比较明显(图 1), 两序列的相关系数达到0.6692, 通过0.01显著性检验。由于样本数只有20个, 因此需用无偏相关系数加以校正, 校正后相关系数为0.6807, 仍通过0.01显著性检验, 说明两指数存在显著的相关关系, 从而可以判断出在得到评价指数的情况下对于反映实际灾情的灾级指数具有一定指示意义。以上这些均表明, 模型能较好地预测和评估台风造成的灾情, 对防灾减灾提供决策依据, 为应急管理提供战略储备。
|
|
| 图 1. 2000-2006年影响浙江省的台风个例评价指数和灾级指数变化 Fig 1. The variety of the disaster grade and evaluation index of every tropical cyclone influence on Zhejiang Province during 2000-2006 | |
5 小结
采用模糊数学建立的热带气旋灾情评估模型, 对2000-2006年影响浙江的台风灾情损失进行评估, 结果表明:评估分布与实际的灾情均很接近, 切实反映出了各因子对实际灾情的影响程度, 表明该模型具有较高的准确率, 是一种较好的灾情评价方法。由于模型中选取的致灾因子均可在灾前得到预测值, 所以灾前政府部门可以利用评估结果积极采取应急措施, 加大防灾减灾力度, 将灾害所造成的社会影响减少到最小。
目前, 我国气象灾害评估工作虽然得到较大的发展, 但仍有很多不完善的地方需要积累经验继续改善, 比如:历史灾情资料的收集、整理困难; 评估指标等级不统一; 评估技术和方法不成熟等。这些都是将来一段时间内应急工作中需要解决并不断创新的关键点。
| [1] | 吕振平, 姚月伟. 浙江省台风灾害及应急机制建设. 灾害学, 2006, 21, (3): 69–71. |
| [2] | 薛根元, 俞善贤, 何风翩, 等. 云娜台风灾害特点与浙江省台风灾害初步研究. 自然灾害学报, 2006, 15, (4): 39–47. |
| [3] | 刘庭杰, 施能, 顾骏强. 浙江省台风灾害的统计分析. 灾害学, 2002, 17, (4): 64–71. |
| [4] | 李春梅, 罗晓玲, 刘锦銮. 层次分析法在热带气旋灾害影响评估模式中的应用. 热带气象学报, 2006, 22, (3): 223–228. |
| [5] | 卢峰本, 黄滢, 许文龙. 影响防城港市的热带气旋灾害评估方法. 广西气象, 2005, 26, (2): 14–15. |
| [6] | 樊琦, 梁必骐. 热带气旋灾害经济损失的模糊数学评测. 气象科学, 2000, 20, (3): 360–366. |
| [7] | 樊琦, 梁必骐. 热带气旋灾情的预测及评估. 地理学报, 2000, 55, (增刊): 52–55. |
| [8] | 冯利华. 灾害损失的定量计算. 灾害学, 1993, 8, (2): 17–19. |
| [9] | 中国气象局. 热带气旋年鉴. 北京: 气象出版社, 2000-2006. |
| [10] | 浙江统计局. 浙江统计年鉴. 北京: 中国统计出版社, 2000-2006. |
| [11] | 曹祥村, 袁群哲, 杨继鉝, 等. 2005年登陆我国热带气旋特征分析. 应用气象学报, 2007, 18, (3): 412–416. |
| [12] | 陈联寿. 热带气旋研究和业务预报技术的发展. 应用气象学报, 2006, 17, (6): 672–681. |
| [13] | Emanuel K, Increasing destructiveness of tropical cyclones over the past 30 years. Nature, 2005, 436: 686–688. DOI:10.1038/nature03906 |
| [14] | 彭祖赠, 孙韫玉. 模糊数学及其应用. 武汉: 武汉大学出版社, 2002: 1-465. |
| [15] | 贺仲雄. 模糊数学与应用. 天津: 天津科技出版社, 1988: 15-75. |
| [16] | 周浩亮. 模糊数学基本理论及其应用. 建井技术, 1994, (21): 70–80. |
| [17] | 梁必骐, 樊琦, 杨洁, 等. 热带气旋灾害的模糊数学评价. 热带气象学报, 1999, 15, (4): 305–311. |
| [18] | 李登峰, 程春田, 陈守煜. 部分信息不完全的多目标决策方法. 控制与决策, 1998, 13, (1): 83–86. |
 2009, 20 (6): 772-776
2009, 20 (6): 772-776