发生干旱的原因是多方面的, 影响干旱严重程度的因子很多, 干旱指标的确定是一个复杂问题, 单一干旱指数无法满足要求。综合气象干旱指数[1]是以标准化降水指数[2]、相对湿润指数和降水量为基础建立的一种综合指数, 它既考虑了降水对干旱的影响, 也考虑了蒸散对干旱的影响, 既考虑了近期(5~10 d) 的水分供需状况, 也考虑了前期 (前30~90 d) 的旱情累积效应, 能够较好地反映气象干旱状况。但计算综合气象干旱指数时需要最近5 d和前30 d的潜在蒸散量, 而潜在蒸散量ET0没有实测值, 只能通过有关公式进行估算。多年来国内外对此开展了大量的对比分析研究[3-6], 提出的估算方法多达几十种, 归纳起来可分为4种类型, 即辐射法、温度法、综合法、蒸发皿法, 其中考虑了能量平衡和水汽扩散理论的Penman-Monteith公式综合反映了蒸发潜热所需要的能量和水汽移动必须具有的动力结构, 具有理论基础坚实, 物理意义明确, 能够反映各气候要素的综合影响等特点, 而且计算结果准确, 适用于不同气候类型地区潜在蒸散量的计算, 1990年, 该方法被FAO专家组成员定为计算潜在蒸散量的标准方法加以推广并不断修正, 我国学者利用此方法在生态环境、作物需水、北方干旱化等方面相继开展了一些研究[7-12], 但由于该公式涉及的气象要素较多, 在实际业务中要实时获得所需全部气象要素非常困难, 因此难于在业务中应用。基于温度资料的ET0估算方法, 简单易行, 便于业务化应用, 但计算精度较差, 国内有些学者, 对一些常用温度法的计算精度作过对比分析[13-16], 由于研究区域不同, 不同学者所得结论也不一致, 说明温度法的估算精度存在明显的地域差异, 本文以综合气象干旱指数的业务化应用为目标, 通过对常用的Thornthw aite温度法和H argreaves温度法的对比, 以期建立可供业务应用的四川省潜在蒸散量估算模型。
1 ET0计算方法比较 1.1 ET0常用计算方法的优缺点目前用于ET0估算的常用方法包括PenmanMonteith法、Thornthwaite法和Hargreaves法。
FAO-56 Penman-Monteith法(简称PM法)是联合国粮农组织推荐计算ET0的标准方法[17], 然而使用PM法计算ET0涉及到最高气温、最低气温、相对湿度、风速、日照时数等多个气象要素, 从气象台站传送的实时资料中无法获得PM公式所需的全部气象数据, 尤其是日照时数数据不能即时获得, 因此在实时业务中该公式无法使用。
Thornthwaite法[18]是一种基于温度的ET0估算方法, 最初基于美国中东部地区的试验数据而提出, 它仅需要月平均气温, 数据容易获得, 但Thornthwaite法计算得到的是月潜在蒸散量, 而计算综合气象干旱指数时不仅需要前1个月的ET0, 而且需要前3个月和近5d的ET0, 用Thornthwaite法计算较为困难。
Hargreaves法[19]也是一种基于温度的ET0估算方法, 在美国西北部较干旱的气候条件下建立, FAO-56推荐在资料缺乏地区计算ET0的替代方法, 该方法仅需要最高、最低气温两个参数, 在气象台站实时资料传输中含有这两个参数, 应用该方法可实现ET0的业务化计算。
1.2 两种基于温度方法的比较在四川盆地和川西高原各选取3个有代表性的站点, 分别采用PM法、Thormthwaite法和Hargreaves法计算各站点1971-2000年逐年逐月的潜在蒸散量, 在此基础上, 计算潜在蒸散量的多年平均值及Thornthwaite法和Hargreaves法计算值与PM法标准值的误差大小, 并对两种基于温度方法的ET0年值序列和月值序列进行对比分析。
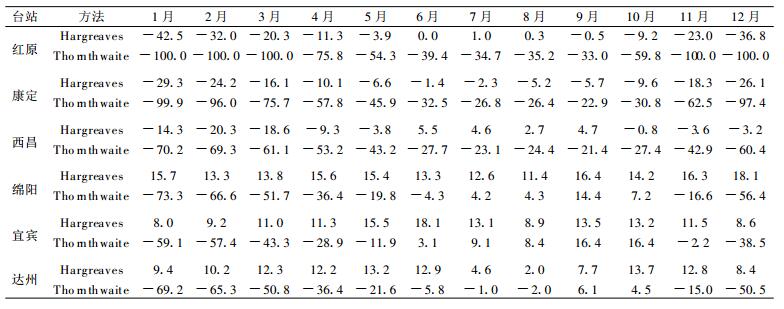
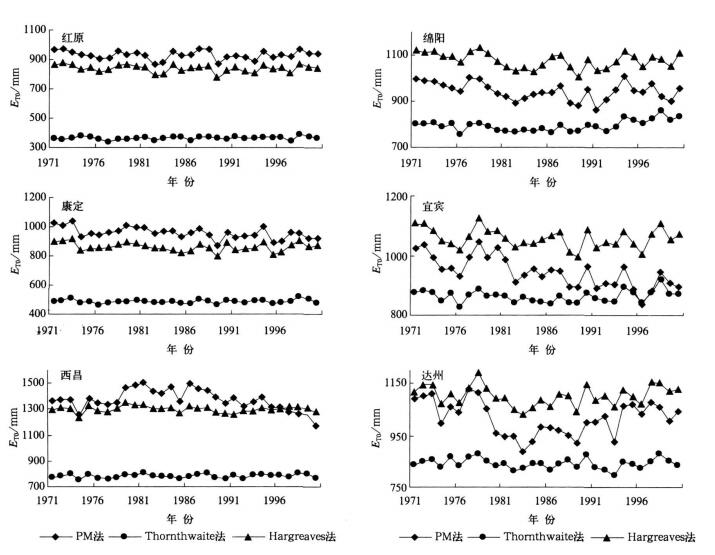
1.2.1 ET0年值比较图 1是PM, Thornthwaite和Hargreaves 3种方法估算的ET0年际变化对比, 由图 1可见:Hargreaves法与PM法的历年变化趋势基本一致, 二者吻合较好, 表明Hargreaves法能较好地反映ET0的年际变化特征, 而Thornthwaite法计算值波动较小, 与PM差异较大, 不能反映ET0的年际变化。Thornthwaite法在川西高原 (红原、康定、西昌) 和四川盆地 (绵阳、宜宾、达州) 均比PM法计算值小, 而Hargreaves法则不同, 在川西高原比PM法计算值小, 在四川盆地则相反。
|
|
| 图 1. PM 法与 Thornthwaite 法和 Hargreaves 法估算的ET0逐年变化 Fig 1. ET0 annual change comparison based on PM, Thornthwaite and Hargreaves | |
|
|
表 1 Thornthwaite法和 Hargreaves 法估算误差比较 (单位:%) Table 1 Estimation error comparison of Thornthwaite and Hargreaves (unit:%) |
表 1给出了Thornthwaite法和Hargreaves法各月ET0估算值与PM法计算值的平均相对误差。对于年潜在蒸散量, 四川盆地和川西高原的Thornthwaite法值均偏小, 四川盆地ET0误差为-10%~-20%, 川西高原则可达-40%~-60%。与Thornthwaite法相比, Hargreaves法计算值的ET0更接近PM法计算值 (宜宾除外), 误差一般为10%~15%, 与Thornthwaite法不同, Hargreaves法在川西高原计算值偏小而在盆地却偏大。
1.2.2 ET0月值比较图 2是PM, Thornthwaite和Hargreaves 3种方法估算的ET0月变化对比, 由图 2和表 1可以看出:川西高原各月Thornthwaite法计算ET0均低于PM法, 而四川盆地夏(秋)季则高于PM法计算值, 且误差大小具有明显的季节特征, 即冬季大, 夏季小, 这是由于Thornthwaite法主要取决于温度高低所致, 冬季由于温度低, Thormthwaite法计算值偏小, 特别是在川西高原, 冬季气温往往低于0℃, 此时Thornthwaite法计算值为0, 误差最大, 达到-100%, 随气温升高, Thornthwaite法计算值逐渐增大, 与PM法计算值差距逐渐缩小, 到夏季, 四川盆地甚至会超过PM法计算值。Hargreaves法计算值在四川盆地各月及西昌6-9月均高于PM法计算值, 而红原、康定两站Hargreaves法计算误差具有明显的冬季大、夏季小的特征, 这与Hargreaves法在高湿地区高估ET0而在高风速地区低估ET0的特性[14]相符。四川盆地属高湿度低风速地区, Hargreaves法高估ET0;而在川西高原南部(西昌)干、湿季分明地区, Hargreaves法在干季 (10月-次年5月)低估ET0, 而湿季(6-9月)高估ET0;在川西高原北部 (红原、康定), 冬季空气干燥、湿度低, 而夏季则相对湿润, Hargreaves法在冬季低估ET0, 而夏季则接近或高于ET0。Hargreaves法与Thornthwaite法比较, 除四川盆地夏(秋)季节Hargreaves法计算误差略大于Thormthwaite法外, 其余季节Hargreaves法误差均显著小于Thornthwaite法, 特别是在川西高原, 这表明, 在四川地区特别是在川西高原, Hargreaves法比Thornthwaite法具有更高的估算精度, Hargreaves法更适合用于四川地区ET0的业务化估算。

|
|
| 图 2. PM 法与 Thornthwaite 法和 Hargreaves 法估算的ET0逐月变化 Fig 2. ET0 monthly change comparison based on PM, Thornthwaite and Hargreaves | |
2 业务化ET0估算模型的建立
PM法是ET0估算的标准方法, 但需要的气象要素较多, 难于业务化应用, Thormthwaite法和Hargreaves法都是基于温度的ET0估算方法, 涉及的气象要素少, 便于业务化应用, 但在四川地区, Thormthwaite法的计算精度较Hargreaves法低, 本文将Hargreaves法作为ET0估算的基本方法, 但FAO-56[14]指出:将Hargreaves法应用于一个新的地区时应用PM法计算结果进行检验, 必要时利用回归分析对月、年计算值求出对该式的校正系数, 由于PM法考虑了风速和湿度大小对ET0的影响, 通常, 用PM法计算比直接用Hargreaves法计算具有更高的估算精度。图 1、图 2和表 1表明, 在四川地区, 无论是年潜在蒸散量还是月潜在蒸散量, Hargreaves法与PM法之间均存在较大误差, 特别是在川西高原冬季误差更大。因此, 本文利用四川省156个气象台站1971 -2000年共4342个ET0_PM(PM法计算的ET0) 和ET0_HG(Hargreaves法估算的ET0)数据对, 以ET0_PM为标准, 应用统计回归方法, 对ET0_HG加以订正, 以建立具有较高精度、可用于业务化应用的四川省ET0估算模型。
在综合气象干旱指数计算中不仅涉及到月和季潜在蒸散量的计算, 而且涉及日潜在蒸散量的计算, 本文主要讨论日潜在蒸散量估算模型的建立, 月、季、年潜在蒸散量由日潜在蒸散量累加而得, 不再另外建立估算模型。
为了提高估算精度, 应建立全年365 d共365个ET0估算模型, 但这样过于繁琐, 实际上, 在1个月的时间间隔之内, 由于气候条件基本相同, 其ET0估算模型的差异很小, 因此, 本文按月建立日潜在蒸散量估算模型。在用PM法和Hargreaves法计算某月的日平均潜在蒸散量时, Tmax, Tmin等相关气象要素均用其日值的月平均值, 而地球外辐射Ra则用该月15日的值代替。
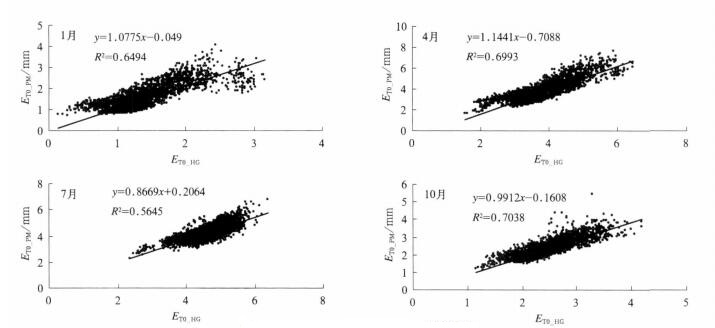
ET0_PM与ET0_HG之间的相关性:图 3所示的是1, 4, 7, 10月ET0_PM与ET0_HG之间的点聚图, 分别代表春、夏、秋、冬4个季节ET0_PM与ET0_HG之间的对应关系。
|
|
| 图 3. ET0_PM与ET0_HG之间的点聚图 Fig 3. Poly-point plan between ET0_PM andET0_HG | |
从图 3可知, ET0_PM与ET0_HG之间均存在明显的线性相关关系, 即两者之间关系式可表达为
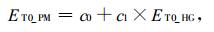
|
(1) |
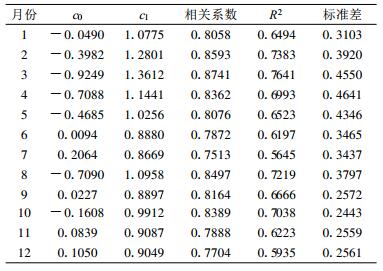
式(1)中, c0, c1为回归系数, 随季节而变, 各月的相关分析结果见表 2。
|
|
表 2 ET0_PM与ET0_HG之间的统计关系 Table 2 Statistics relation between ET0_PM and ET0_HG |
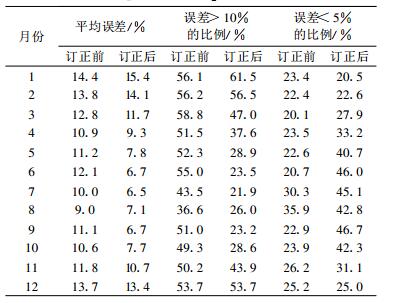
表 2所示各月相关系数均在0.75以上, 通过0.05显著性检验。将表 2所列回归系数代入式(1), 对1971-2000年逐日ET0_HG加以订正, 并计算出订正后的逐月ET0, 再与PM法计算的ET0值进行比较, 比较结果见表 3。
从表 3可见:3-11月, 订正后的误差平均值比订正前有所降低, 误差大于10%所占的比例减少较多, 而误差小于5%所占的比例则有较大提高, 这表明订正后的ET0估算精度总体好于订正前的估算精度, 但误差仍然较大, 11月-次年3月平均误差都在10%以上, 特别是1-2月, 订正后的误差反而比订正前大, 其原因是川西高原1-2月是全年湿度最低的月份, 而此时风速也相对较大(略小于最大的3 -4月), 致使此时Hargreaves法低估ET0最突出, 鉴于此, 必须作进一步的订正。
|
|
表 3 订正前后ET0_HG的精度比较 Table 3 Error comparison of ET0_HG before and after revised |
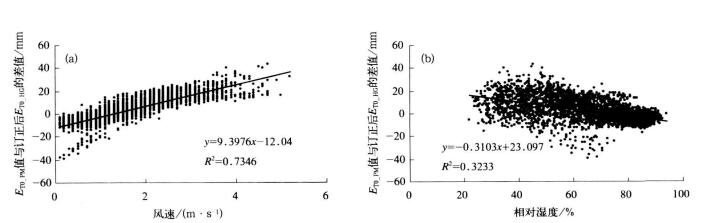
由于ET0_HG没有考虑风和空气湿度对蒸散的影响, 因此, 它与ET0_PM值的差异必定与风速和湿度有关, 图 4给出了1月ET0_PM值减去订正后ET0_HG值的差值与月平均风速和月平均相对湿度的对应关系。
从图 4可以看出:ET0_PM与ET0_HG的差值与风速和相对湿度确实存在明显的线性关系, 因此, ET0_PM可进一步估算:
|
|
| 图 4. 订正后 ET0与风速(a)和湿度(b)的关系 Fig 4. Relationship of revised ET0 to wind speed(a)and humidity(b), respectively | |
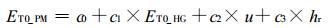
|
(2) |
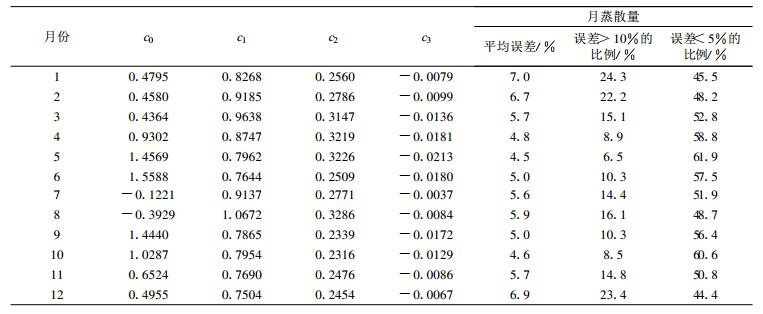
式(2)中, ET0_PM为PM法计算的日蒸散量, ET0_HG为Hargreaves法计算的日蒸散量, u为日平均风速, hr为日平均相对湿度, c0, c1, c2, c3为回归系数。根据式(2)所建立的各月ET0估算模型及估算精度见表 4。
从表 4可见:风速与蒸散呈正相关(c2为正), 而空气湿度与蒸散呈负相关(c3为负)。对比表 4与表 3发现:引入风速和湿度后, 误差大于10%所占的比例显著降低, 而误差小于5%所占的比例显著提高, 与此同时, 各月蒸散量的平均误差均在下降, 特别是11月-次年3月下降更为显著, 全年各月平均误差均降到了10%以下。就误差分布来看(以1月为例, 其他月份类似, 图略):引入风速和湿度之前, 误差较大, 地域特征明显, 四川盆地大部为10%~20%, 川西高原一般都在-10%以下, 在川西高原东北、西北部和西南部, 误差都在-20 %以下, 引入风速和湿度之后, 误差显著降低, 四川省绝大部分地区都在-10 %~10 %之间, 由此表明:引入风速和湿度之后, ET0的估算精度有了明显提高, 误差可以控制在10%以内, 能够用于业务应用。
|
|
表 4 ET0业务化估算模型及估算精度 Table 4 ET0 operational model and estimation accuracy |
3 应用实例
根据式(2)和表 4所列回归系数, 对2006年四川省特大伏旱期间的潜在蒸散量进行估算, 并利用综合气象干旱指数进行旱情的逐日跟踪监测, 从逐日旱情分布图(略)可以看出:7月中旬开始出现旱情, 7月下旬旱情发展加重, 受旱区域扩大, 到8月中旬旱情发展到鼎盛阶段。此时, 受旱区域最广, 旱情强度最强, 到9月上旬, 大部分地方的旱情都得到缓解或解除, 这一监测结果, 比较真实地反映了当时的旱情发展状况, 与同期农业气象站点的土壤墒情观测数据对比发现, 旱情重的地区土壤墒情普遍较差, 而旱情轻的地区土壤墒情普遍较好, 以土壤墒情60%作为干旱的划分标准, 两者受旱站点的吻合程度在70%以上, 这表明用本文建立的ET0估算模型计算的综合气象干旱指数, 对四川省气候干旱有较好的监测能力。
4 小结本文对比分析了PM法、Thormthwaite法和Hargreaves法3种潜在蒸散量(ET0) 估算方法的优劣, 提出了可供业务化应用的潜在蒸散量估算模型, 并通过实例对ET0估算模型和综合气象干旱指数监测四川省旱情的可靠性和可行性进行了验证, 主要结论如下:
1) PM法是估算潜在蒸散量的标准方法, 但其涉及的气象要素较多, 目前无法实现业务化应用;Thormthwaite法和Hargreaves法都是基于温度的ET0估算方法, 涉及的气象要素少, 便于业务化应用, 但对四川地区来说, Thormthwaite法的估算值显著偏低, 其估算精度远不及Hargreaves法的精度高, 在川西高原更是如此。
2) Hargreaves法估算值与PM法标准值之间存在显著正相关关系, 经线性订正后, Hargreaves法估算值的精度总体有所提高, 但误差仍然较大, 特别是冬季, 订正效果不明显。
3) PM法标准值与Hargreaves法估算值之间的差异是由于Hargreaves法没有考虑风速和空气湿度对潜在蒸散量的影响造成的, 这种差异与风速呈显著正相关, 而与空气湿度呈显著负相关, 将风速和空气湿度引入订正模型后, 订正效果显著改善, 平均相对误差能够控制在10%以内。
4) 基于ET0业务化估算模型计算的综合气象干旱指数对四川省干旱具有一定的监测能力, 所反映的旱情分布与土壤墒情信息基本一致, 可在业务中加以应用
| [1] | 张强, 高歌. 我国近50年旱涝灾害时空变化及监测预警服务. 科技导报, 2004, 7: 21–24. |
| [2] | 张顺谦, 侯美亭, 王素艳. 基于信息扩散和模糊集方法的四川盆地气候干旱综合评价. 自然资源学报, 2008, 23, (4): 713–723. |
| [3] | Jensen M E, Burman R D, Allen R G, Evapotranspiration and Irrigation Water Requirements. ASCEManuals and Reports on Engineering Practice, 1990, 70: 332. |
| [4] | 李玉霖, 崔建垣, 张铜. 参考作物蒸散量计算方法的比较研究. 中国沙漠, 2002, 22, (4): 372–376. |
| [5] | 刘绍民, 孙中平, 李小文, 等. 蒸散量测定与估算方法的对比研究. 自然资源学报, 2003, 18, (2): 161–167. |
| [6] | 毛飞, 张光智, 徐祥德. 参考作物蒸散量的多种计算方法及其结果的比较. 应用气象学报, 2000, 11, (增刊): 128–136. |
| [7] | 郭建平, 高素华, 毛飞. 中国北方地区干旱化趋势与防御对策研究. 自然灾害学报, 2001, 10, (3): 32–36. |
| [8] | 封志明, 杨艳昭, 丁晓强, 等. 甘肃地区参考作物蒸散量时空变化研究. 农业工程学报, 2004, 20, (1): 99–103. |
| [9] | 高歌, 陈德亮, 任国玉, 等. 1956~2000年中国潜在蒸散量变化趋势. 地理研究, 2006, 25, (3): 378–387. |
| [10] | 杨启国, 张旭东, 杨兴国, 等. 旱作小麦农田实际蒸散量计算模式研究. 干旱地区农业研究, 2005, 23, (1): 34–38. |
| [11] | 吕厚荃, 钱拴, 杨霏云, 等. 华北地区玉米田实际蒸散量的计算. 应用气象学报, 2003, 14, (6): 722–728. |
| [12] | 马晓群, 张辉. 近30年安徽省地表干湿时空变化及对农业影响. 应用气象学报, 2007, 18, (6): 783–790. |
| [13] | 王新华, 郭美华, 徐中民. 分别利用Hargreaves和PM公式计算西北干旱区ET0的比较. 农业工程学报, 2006, 22, (10): 21–25. |
| [14] | 丁加丽, 彭世彰, 徐俊增, 等. 基于温度资料的参考作物蒸发蒸腾量计算方法. 河海大学学报 (自然科学版), 2007, 35, (6): 633–637. |
| [15] | 刘晓英, 李玉中, 王庆锁. 几种基于温度的参考作物蒸散量计算方法的评价. 农业工程学报, 2006, 22, (6): 12–18. |
| [16] | 范丽萍, 贾忠华, 罗纨, 等. 西安地区Priestley-Taylor和Hargreaves方法应用比较. 水资源与水工程学报, 2007, 18, (2): 53–57. |
| [17] | Allen R G, Pereira L S, Raes D, et al. Crop Evapotran spiration-Guidelines for Computing Crop Water Requirements FAO Irrigation and Drainage. Paper No.56 (Electric Publication). Rome:FAO, 1998. |
| [18] | Thornthwaite C W, An approach toward a rational classification of climate. Geographic Review, 1948, 38: 55–94. |
| [19] | Hargreaves G H, Samani Z A, Reference crop evapotranspiration from temperature. Applied Engineering in Agriculture, 1985, 1, (2): 96–99. DOI:10.13031/2013.26773 |
 2009, 20 (6): 729-736
2009, 20 (6): 729-736