应用气象学报  2009, 20 (6): 706-712   PDF    
引用本文
林春泽, 智协飞, 韩艳, 王靖宇. 基于TIGGE资料的地面气温多模式超级集合预报[J]. 应用气象学报, 2009, 20(6): 706-712.
Lin Chunze, Zhi Xiefei, Han Yan, Wang Jingyu. Multi-model Superensemble Forecasts of the Surface Temperature Using the TIGGE Data[J]. Journal of Applied Meteorological Science, 2009, 20(6): 706-712  
基于TIGGE资料的地面气温多模式超级集合预报
林春泽1,2, 智协飞1, 韩艳1, 王靖宇1     
1. 南京信息工程大学, 南京 210044;
2. 中国气象局武汉暴雨研究所, 武汉 430074
2009-01-04 收到, 2016-01-13 收到修改稿.
资助项目: 2007年度公益性行业 (气象) 科研专项“面向TIGGE的集合预报关键应用技术研究”(GYHY (QX)2007-6-1) 和2005年江苏省“六大人才高峰”项目共同资助    
摘要: 基于TIGGE资料, 采用均方根误差分别对欧洲中期天气预报中心、日本气象厅、美国国家环境预报中心和英国气象局4个中心集合预报的地面气温场集合平均结果进行检验评估, 比较各中心地面气温的预报效果。并利用超级集合、多模式集合平均和消除偏差集合平均3种方法对4个中心的地面气温预报进行集成, 同时对预报结果进行分析。结果表明: 2007年夏季日本气象厅与欧洲中期天气预报中心在北半球大部分地区预报效果最好, 各中心在不同地区预报效果不同。超级集合与消除偏差集合平均降低了预报误差, 预报效果优于最好的单个中心预报和多模式集合平均。对于较长的预报时效, 消除偏差集合平均表现出了更好的预报性能。
关键词: TIGGE    集合平均    超级集合    消除偏差集合平均    
Multi-model Superensemble Forecasts of the Surface Temperature Using the TIGGE Data
Lin Chunze1,2, Zhi Xiefei1, Han Yan1, Wang Jingyu1     
1. Nanjing University of Information Science & Technology, Nanjing 210044;
2. Wuhan Institute of Heavy Rain, CMA, Wuhan 430074
Abstract: Based on the TIGGE data, the ensemble mean outcomes of the 24-168 hours ensemble forecasts for the surface temperature in the Northern Hemisphere during the summer of 2007 are provided by ECMWF, JMA, NCEP and UKMO. Root-mean-square errors (RMSE) of the results are examined.The multi-model ensemble forecasts of the surface temperature for the forecast period from August 1 to 31 of 2007 are conducted by utilizing the superensemble, the multi-model ensemblemean, and the bias-removed ensemble mean.The forecast skills of these multi-model ensemble methods are investigated.The results show that the JMA model performs best for 24-hour and 48-hour forecasts, but for 72-hour to 168-hour forecasts the ECM WF model is the one with the highest skill. Forecast skills of these four models of different operational forecast centers are quite different over various regions.The JMA model performs best in the United States and Europe, while in China the UKMO model is the best one. Actually, none of the four models is perfect for all regions in the Northern Hemisphere.Therefore, it is necessary to utilize the multi-model superensemble methodology to improve the forecast skill. The multi-model superensemble and the bias-removed ensemble mean reduce the RMSE of the surface temperature forecast considerably.Both methods show an improvement on the forecast skill over the best single model forecast and the multimodel ensemblemean.In early (late) phase of the forecast period, the multi-model superensemble produces a smaller (larger) RMSE than the bias-removed ensemble mean for the 24-hour and 48-hour forecasts.For the 72-hour to 168-hour forecasts, both the multi-model superensemble and the the bias-removed ensemble mean lead to smaller RMSE than the multi-model ensemble mean and single models during the first two weeks of the forecast period.Never theless, two weeks later the RMSE of the superensemble forecast increases rapidly, and exceeds that of the bias-removed ensemble mean.The RMSE of the multi-model superensemble forecast may even exceed that of the single model forecast at the end of the forecast period. Weight coefficients of multi-model superensemble methodology remain unchanged during the fixed training period. It's expected that an improved multi-model superensemble methodology with flexible training period when statistical weights of the multi-models vary with time may further improve the forecast skill.
Key words: TIGGE     ensemble mean     superensemble     bias-removed ensemble mean    
引言

Lorenz[1]最早提出集合数值预报的思想, Leith[2]将Lorenz的非线性理论与Epstein[3]的动力随机预报理论方法相结合, 提出了可用于实际预报的蒙特卡罗方法。从此, 集合数值天气预报开始由理论研究向实际应用迈进。进入20世纪90年代, 集合预报技术在许多国家气象部门相继投入业务使用。近年来, 世界气象组织 (WMO)发起的THO RPEX科学计划中的TIGGE计划提出了建立全球交互式大集合预报, 以改进1~14d天气预报。中国气象局、欧洲中期天气预报中心和美国国家大气研究中心作为WMO设立的3个TIGGE资料中心, 每天接收数十个国家的集合预报资料。比较各中心的预报效果和如何充分利用各中心的集合预报资料提高预报准确率已成为各国气象部门的研究热点。多模式集合技术是一个充分利用各中心模式预报结果以减小模式系统性偏差的有效途径, 而超级集合预报技术又是目前预报效果最好的方法之一。Krishnamurti等[4]最早提出超级集合预报方法, 对于某一气象要素预报, 在每一个格点上, 超级集合方法根据参与集合的各个模式在该格点上训练期的表现分配不同的统计权重[5]。然后, 这些权重被用于预报期进行多模式超级集合预报, 效果好的模式获得权重多, 而效果差的模式获得权重少, 从而降低单个模式的偏差, 提高预报准确率。该方法具有有效改进短期气候预测技巧、提高中短期预报准确率和简便实用等优点, 在国际上得到了广泛研究与应用[5-10]。

超级集合预报属于一种非等权的集成预报方法。随着我国数值预报技术的发展, 包括该方法在内的各种集成预报方法成为我国气象工作者的研究热点[11-16]。陈丽娟等[13]借用超级集合思想对我国汛期降水预测的各大单位预报结果进行集成, 结果表明:集合预报效果比较稳定, 多数情况下优于单个成员预报。赵声蓉[14]应用神经网络方法对3个国家不同的业务模式2m温度预报进行集成试验, 发现集成的温度预报效果明显好于单个模式的预报, 并且不存在明显的系统误差。

本文主要对欧洲中期天气预报中心(ECMWF)、日本气象厅(JMA)、美国国家环境预报中心(NCEP)以及英国气象局(UKMO)4个中心集合预报资料中, 地面气温场的集合平均结果进行检验评估, 并对4个中心的地面气温预报进行超级集合预报试验, 分析超级集合预报误差, 并同各个模式的集合平均及多模式等权平均结果的误差进行比较。

1 资料和方法 1.1 资料

本文所用资料包括ECMWF, JMA, NCEP和UKMO集合数值预报资料的集合平均资料以及NCEP/NCAR再分析资料。

① TIGGE资料:选取4个中心全球集合预报模式2007年6月1日-8月31日逐日12:00(世界时, 下同) 起报的地面气温的各自集合平均资料, 预报区域为10°N以北所有区域, 分辨率为2.5°×2.5°, 预报时效为24~168 h, 间隔为24h。

② NCEP/NCAR再分析资料:选取2007年6月1日-9月7日逐日12:00地面气温资料, 格点分辨率与预报资料相同, 用于检验预报效果。

1.2 方法

超级集合预报方法将选取的时间序列分为两部分, 即训练期和预报期。在训练期使用超级集合预报值与观测值做多元线性回归分析, 确定参与超级集合的各个模式的回归(权重)系数, 权重随空间变化随时间不变, 相应的权重系数用于预报期的超级集合预报[6-8]。

超级集合预报模型由式(1)构建, 在一个给定的格点上, 对于某一预报时效某一气象要素有:

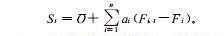
(1)

式(1)中, St为超级集合预报值, O为训练期观测值平均, ai为回归系数(权重), Fi, t为第i个模式的预报值, Fi为第i个模式在训练期的预报值平均, n为参与超级集合的模式总数, t为时间。

在训练期, 回归系数ai由式(2)中的误差项G最小化计算而得[8] :

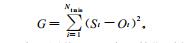
(2)

式(2)中, Ot为观测值, Ntrain为训练期时间样本总数。在预报期, 将在训练期得到的ai代入到式(1) 中, 对其他格点也做同样的计算, 即可进行超级集合预报。

几种常规的多模式集合方法包括简单的多模式集合平均(EMN)、消除偏差集合平均(BRE)等[8]。简单的多模式集合平均可由式(3)定义, 消除偏差集合平均可由式(4)定义:

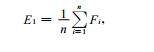
(3)
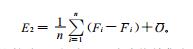
(4)

比较式(1)与式(4), 消除偏差集合平均给予参与集合的每个模式相同权重, 好的模式与差的模式对集合预报的贡献相同, 而超级集合通过各个模式在训练期表现给予不同的权重来量化它们对集合预报的贡献, 好的模式给予的权重多, 差的模式给予的权重少。进行超级集合预报试验时可以根据这两种方法做对比分析, 以评价超级集合预报技巧。

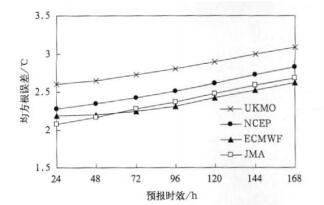
2 地面气温集合预报误差评估

以温度预报的均方根误差作为衡量预报效果的指标, 计算2007年6月1日-8月31日4个中心地面气温预报在北半球大部地区(10°~87.5°N, 0°~357.5°)的区域平均均方根误差。如图 1所示, 对于北半球大部地区4个中心预报的均方根误差随预报时效增加而增大, 但增幅并不大, 预报时效从24 h增加到168 h均方根误差增加0.5 ℃左右, UKMO误差最大, NCEP次之, ECMWF与JMA的误差最小。JMA的24h, 48 h预报效果最好, 误差为2.07℃和2.16℃。UKMO的24h, 48h预报效果最差, 误差为2.6℃和2.65℃。4个中心中, ECMWF的72~168 h预报误差最小, 预报效果最好。

图 1. 2007年6月1日-8月31日地面气温预报在北半球区域平均均方根误差 Fig 1. The mean RMS error of the surface temperature forecast in the Northern Hemisphere from 1 June to 31 August 2007

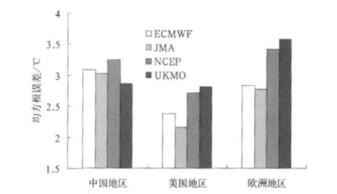
分别计算2007年6月1日-8月31日中国(15°~55°N, 70°~135°E)、美国(25°~55°N, 125°~70°W)和欧洲(30°~55°N, 0°~40°E)3个地区各中心地面气温预报的区域平均均方根误差, 图 2为72 h地面气温预报在3个区域的平均均方根误差。由图 2可知, 在中国地区, UKMO预报的均方根误差小于其他3个中心, 预报效果最好, ECMWF与JMA比较接近, NCEP误差最大。在美国地区, JMA的预报效果最好, UKM O最差, JMA72h预报均方根误差比UKMO小0.66℃左右。在欧洲地区, JMA的预报效果最好, 其次是ECMWF, UKMO的预报均方根误差最大。这表明, 不同模式在不同地区的预报性能各有优劣, 并不存在任何地区都优于其他模式的“完美”模式。对于其他预报时效, 也可以得到类似的结论(图略)。因此, 使用多模式集成预报方法降低预报误差显得尤为必要。

图 2. 2007年6月1日- 8月31地面气温72h预报区域平均均方根误差 Fig 2. The mean RMS error of the surface temperature 72-hour forecast in China, USA and Europe from 1 June to 31 August 2007

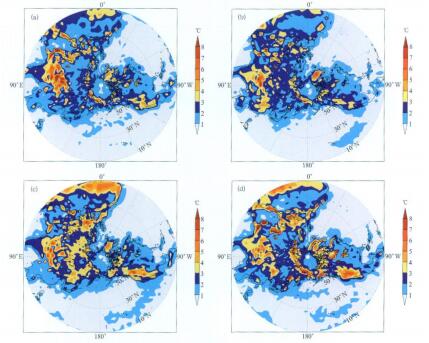
图 3给出2007年6-8月共92d4个中心24h地面气温预报均方根误差在北半球的分布。从图 3可见, 每个中心的地面气温预报均方根误差在亚洲大陆地区误差都较大, 在北美地区较小。均方根误差在2℃以下的区域ECMWF最大, 均方根误差在3℃以下的区域JMA最大。比较4个中心地面气温预报均方根误差分布可以看到, ECM WF和JMA的地面气温预报的均方根误差比其他中心小, 48h和72h的均方根误差分布(图略)与24h情况基本一致。96h, 120h, 144h, 168h地面气温预报的均方根误差地理分布(图略)也与24h基本一致, ECMWF的均方根误差分布差异较其他3个中心更小。

图 3. 2007年6月1日-8月31日ECMWF（a），JMA（b），NCEP（c）和UKMO（d）地面气温24h预报均方根误差地理分布 Fig 3. Dist ribution of the RMS error of the 24 -hour surface temperature fo recast for ECMWF(a), JMA(b), NCEP(c)and UKMO(d)from 1 June to 31 August 2007

3 超级集合预报试验结果

通过对4个中心的地面气温预报效果检验, 可以了解到各个中心在不同区域的预报效果不同, 各个中心的数值预报模式都有系统性偏差。针对4个中心的地面温度预报, 选取6月1日-7月31日作为训练期, 8月1-31日作为预报期, NCEP/NCAR再分析资料的地面气温资料作为观测值, 进行超级集合预报(SUP)试验。同时, 应用多模式集合平均(EMN)和消除偏差集合平均(BRE)两种方法对4个中心的预报进行集成, 比较这3种多模式集成方法的预报效果, 并对超级集合预报结果进行分析。

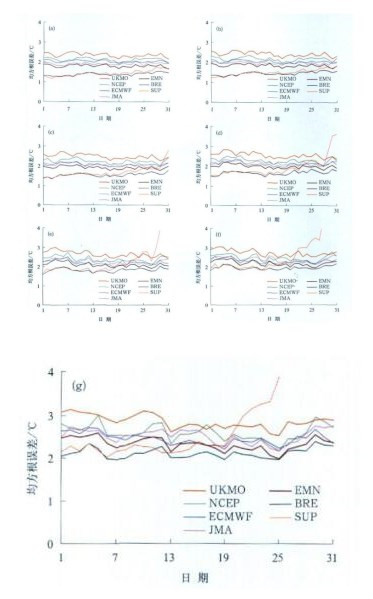
图 4分别给出了研究区域预报期8月1-31日预报时效为24~168h4个中心和3种集合方法地面温度预报每天的区域平均均方根误差。由图 4可知, 24h, 48h的预报3种集成方法都降低了预报误差, 超级集合预报与消除偏差集合预报平均效果明显好于各个中心的预报。在预报期, 超级集合预报与消除偏差集合预报平均均方根误差随预报时间的后移有递增趋势, 两种方法预报效果相当。预报期的前几天超级集合预报效果略好于消除偏差集合平均, 但差异不太明显。两种方法在预报期的均方根误差比多模式集合平均的误差降低了0.5℃左右, 明显优于多模式集合平均预报。超级集合与消除偏差集合平均72~96 h的预报效果相当, 在预报期的后几天, 超级集合预报的均方根误差增长很快, 超过了消除偏差集合平均预报。120~168 h的预报, 在预报期的前半段, 超级集合预报与消除偏差集合平均预报均好于各中心集合预报及4个中心的集合平均, 但随着预报时间的后移, 超级集合预报的均方根误差增长较快, 在预报期的后期超过了4个中心集合平均和各中心的集合预报。

图 4. 2007年8月1-31日24h(a), 48h(b), 72h(c), 96h(d), 120h(e), 144h(f)和168h(g)地面温度预报区域平均均方根误差 Fig 4. The mean RMS error of the surface temperature forecast for 24 hours(a), 48hours(b), 72 hours(c), 96 hours(d), 120 hours(e), 144 hours(f)and 168 hours(g)from 1 June to 31 August 2007

综上所述, 超级集合与消除偏差集合平均两种方法对24h, 48h预报改善的效果相当, 在预报期前期, 超级集合预报的均方根误差小于消除偏差集合平均的误差, 但后期超级集合预报的均方根误差超过了消除偏差集合平均的误差。对于72~168h预报, 预报期前两周超级集合预报的均方根误差和消除偏差集合平均的误差相当, 两周后超级集合预报的均方根误差增长很快, 超过了消除偏差集合平均的误差。

图 5分别给出了JMA集合预报、多模式集合平均、消除偏差集合平均和超级集合在31 d预报期内地面气温24 h预报平均均方根误差分布。从图 5可见, 多模式集合平均对降低误差效果并不明显。超级集合预报均方根误差大于3℃的区域明显减少, 多模式超级集合有效地减小了预报误差, 好于最好的JMA预报和集合平均预报。超级集合预报与消除偏差集合平均预报的均方根误差分布较为一致, 两种方法预报效果相当。对于48 h的预报(图略), 超级集合预报与消除偏差集合平均预报改善了预报效果, 好于单个中心集合预报和4个中心的集合平均, 消除偏差集合平均预报的均方根误差大值区域小于超级集合预报。

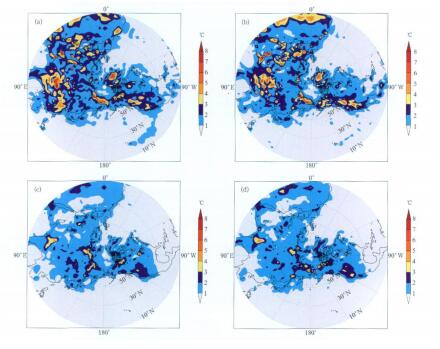
图 5. 2007年8月1-31日JMA集合预报(a)、多模式集合平均(b)、消除偏差集合平均(c)和超级集合(d)地面温度24h预报平均均方根误差分布 Fig 5. Distribution of the RMS error of 24-hour surface temper ature forecast for JMA(a), EMN(b), BRE(c)and SUP(d)from 1 to 31 August 2007

4 结论与讨论

本文对ECMWF, JMA, NCEP, UKMO2007年夏季的24~168h全球集合预报中地面温度场的集合平均结果进行了评估, 并对4个中心地面温度预报进行超级集合预报试验, 比较了多模式超级集合与多模式集合平均、消除偏差集合平均的预报效果, 得到以下结论:

1)2007年夏季, 各中心集合预报地面气温预报效果明显不同, JMA的24h, 48h预报误差最小, ECMWF的72~168h预报误差最小, 预报效果最好。在中国地区, UMKO预报效果最好, 在美国和欧洲地区, JMA的预报效果最好。

2)4个中心的集合平均在一定程度上减小了各中心预报的系统性误差, 预报效果优于最好的单个中心预报, 但预报效果的改善不明显。消除偏差集合平均使预报的均方根误差得到明显降低, 预报效果优于最好的单个中心预报和集合平均。

3) 多模式超级集合与消除偏差集合平均两种方法对24h, 48 h预报改善的效果相当。对于72~168h预报, 在预报期前期两者相当, 但随着预报期的增长超级集合预报误差增长很快, 而消除偏差集合平均预报较为稳定。

超级集合预报的权重系数随空间变化, 但随时间不变。选取2007年6-7月共61d作为训练期计算权重系数, 用于2007年8月的预报, 权重系数随着预报时间后移会逐渐失效, 尤其当预报时效较长时, 权重系数失效得更快, 导致预报误差快速增长。预报期前期, 超级集合的预报误差都较小。这表明, 如果采用滑动训练期, 权重系数随时间变化, 有可能进一步改善超级集合预报效果。

致谢 感谢德国波恩大学气象系Andreas Hense教授提供优越的客座研究条件, Jan Keller博士帮助处理了部分集合预报资料。
参考文献
[1] Lorenz E N, A study of the predictability of 28-variable atmosphere model. Tellus, 1969, 21: 739–759.
[2] Leith C E, Theoretical skill of Monte Carlo forecasts. Mon Wea Rev, 1974, 102: 409–418. DOI:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2
[3] Epstein E S, Stochastic dynamic prediction. Tellus, 1969, 21: 739–759.
[4] Krishnamurti T N, Kishtawal C M, LaRow T, et al. Improved weather and seasonal climate forecasts from multimodel superensemble. science, 1999, 285: 1548–1550. DOI:10.1126/science.285.5433.1548
[5] Vijaya Kumar T S V, Sanjay J, Basu B K, et al. Experimental superensemble forecasts of tropical cyclones over the Bay of Bengal. Nat Hazards, 2007, 41: 471–485. DOI:10.1007/s11069-006-9055-4
[6] Krishnamurti T N, Kishtawal C M, Shin D W, et al. Improving tropical precipitation forecasts from multianalysis superen semble. J Climate, 2000, 13: 4217–4227. DOI:10.1175/1520-0442(2000)013<4217:ITPFFA>2.0.CO;2
[7] Krishnamurti T N, Kishtawal C M, Zhan Zhang, et al. Multimodel ensemble forecasts for weather and seasonal climate. J Climate, 2000, 13: 4197–4216.
[8] Cartwright T J, Krishnamurti T N, Warm season mesoscale superensemble precipitation forecasts in the southeastern United States. Wea Forecasting, 2007, 22: 873–886.
[9] Krishnamurti T N, Gnanaseelan C, Chakraborty A, Prediction of the diurnal change using a multimodel superensemble. Mon Wea Rev, 2007, 135: 3613–3632.
[10] Yun W T, Stefanova L, Krishnamurti T N, Improvement of the multimodel superen semble technique for seasonal forecasts. J Climate, 2003, 16: 3834–3840. DOI:10.1175/1520-0442(2003)016<3834:IOTMST>2.0.CO;2
[11] 魏凤英. 全国夏季降水区域动态权重集成预报实验. 应用气象学报, 1999, 10, (4): 402–409.
[12] 陈丽娟, 许力, 王永光. 超级集合思想在汛期降水预测集成中的应用. 气象, 2005, 31, (5): 52–54.
[13] 陈丽娟, 王盘兴. 一种新的集合预报权重平均方法. 应用气象学报, 2006, 17, (4): 488–493.
[14] 赵声蓉. 多模式温度集成预报. 应用气象学报, 2006, 17, (1): 52–58.
[15] 周兵, 赵翠光, 赵声蓉. 多模式集合预报技术及其分析与检验. 应用气象学报, 2006, 17, (增刊): 104–109.
[16] 马清, 龚建东, 李莉, 等. 超级集合预报的误差订正与集成研究. 气象, 2008, 34, (3): 42–48.