应用气象学报  2009, 20 (6): 692-698   PDF    
引用本文
张强, 熊安元, 张金艳, 冯明农, 王伯民. 晴雨(雪) 和气温预报评分方法的初步研究[J]. 应用气象学报, 2009, 20(6): 692-698.
Zhang Qiang, Xiong Anyuan, Zhang Jinyan, Feng Mingnong, Wang Bomin. Preliminary Study on the Scoring Methods of Cloud-free Rainfall/Snowfall and Air Temperature Forecasts[J]. Journal of Applied Meteorological Science, 2009, 20(6): 692-698  
晴雨(雪) 和气温预报评分方法的初步研究
张强1, 熊安元1, 张金艳2, 冯明农1, 王伯民1     
1. 国家气象信息中心, 北京 100081;
2. 国家气象中心, 北京 100081
2008-09-23 收到, 2009-09-15 收到修改稿.
资助项目: 中国气象局2007年度多轨道业务建设项目“多轨道业务产品检验及效果评估”(910208002001) 和2008年中国气象局业务建设项目“预报预测体系产品检验及质量评分”(200209003002-001) 共同资助    
摘要: 利用全国逐日天气预报产品和对应实况数据, 分析了目前普遍使用的晴雨(雪) 和气温预报评分方法存在的问题, 并进行了改进尝试和研究。结果表明:由于没有考虑降水概率的影响, 在降水概率全国差异较大的多数月份, 晴雨(雪) 预报正确率与单站无降水频率表现为正相关, 具有无降水频率越大评分越高的趋势; 采用绝对标准值(1 ℃或2 ℃) 作为阈值进行气温预报准确率评分, 评分结果与气温日际变化呈明显负相关, 气温日际变化偏小则评分值偏高的趋势比较明显。该文提出的晴雨(雪) 和气温预报改进评分方法能有效减少降水概率和气温日际变化对晴雨(雪) 和气温预报评分的影响, 提高不同气候背景地区天气预报评分结果的可比性, 在天气预报质量检验和评估业务中具有一定的应用和推广价值。
关键词: 晴雨(雪)    气温    天气预报    评分方法    
Preliminary Study on the Scoring Methods of Cloud-free Rainfall/Snowfall and Air Temperature Forecasts
Zhang Qiang1, Xiong Anyuan1, Zhang Jinyan2, Feng Mingnong1, Wang Bomin1     
1. National Meteorological Information Center, Beijing 100081;
2. National Meteorological Center, Beijing 100081
Abstract: Scientific and reasonable forecast scoring method is fundamental for evaluating the efficiency of the weather forecast objectively.By comparing forecast results with the corresponding observed data of 373 stations in China, the problems in existing forecast scoring method of the cloud-free rainfall/snow fall and temperature are investigated. Experimental amendments are made to the method, too. As a widely used method, forecast accuracy of the cloud-free rainfall/snowfall proves to be simple and practical in judging the effects of forecast to some extent.But without considering influence of rainfall probability, the forecast accuracy cannot distinguish blind prediction or persistent prediction accuracy effectively, and may bring abnormal high value even some mistakes.Skill-score of the cloud-free rainfall/snowfall forecast accuracy is positively correlated to the no-rainfall frequency at a single station during the months when regional rainfall probability difference is significant. In terms of temperature forecast, daily variation of the air temperature is a significant factor that affects the skill-score.When adopting 1℃ or 2℃ as the absolute standard value threshold, the skill-score of temperature forecasting is negatively correlated to the daily temperature variation. PF method and Index Threshold method are proposed in order to reduce the influences of rainfall probability and daily temperature variation.The results indicate the forecast score of precipitation by PF method is not closely correlated with rainfall frequency at single station during the months when regional rainfall probability difference is dominant in China. When adopting 2/3 or 1/2 as the index threshold, the linear regression coefficient between the daily temperature variation and the temperature forecast score can be significantly reduced.The correlation coefficient also decreases obviously with the value down to below 0.15, which is clearly lower than adopting the absolute standard value threshold. In other words, skill-score of temperature forecast using Index Threshold method is less sensitive to the daily temperature variation than using forecast accuracy method. Above all, the new methods proposed can effectively reduce the influences of rainfall probability and daily temperature variation on the skill-score of the cloud-free rainfall/snowfall and air temperature. It also improves the comparability of the weather forecast scores in the regions with different climate background. Therefore, it can be applied to the quality test and assessment on the weather forecast.
Key words: cloud-free rainfall/snowfall     temperature     weather forecast     forecast scores    
引言

天气预报作为气象部门重要的社会公益服务产品, 越来越受到社会和公众的广泛关注。为提高天气预报准确率, 增加社会满意度, 我国各级气象部门和广大气象科技人员进行了长期不懈的努力, 进行了许多思考和探讨[1-6]。近几年, 越来越多的地方气象部门通过建立天气预报质量评分系统[7-9], 开展天气预报的质量检验工作, 这对提高地方天气预报水平起到了积极的作用。2007年, 中国气象局专门设立了业务建设项目“多轨道气象业务产品检验及效果评估”, 在该项目支持下, 国家气象信息中心成功建立了国家级气象业务产品质量检验平台, 并基于该平台对全国天气预报产品开展了定期质量检验和评估业务, 这对促进和提高全国天气预报水平具有积极作用。

对天气预报的质量进行检验和评估, 根据检验和评估的不同对象和目的, 可以采用不同方法。不同的质量评分方法从不同侧面或角度表现了天气预报的质量和效果, 具有其各自的长处和短处。中国气象局于1990年下发了《重要天气预报质量评分办法》, 对主要天气现象预报检验制定了一套详细的评分方法, 但使用中发现存在一些问题[10-11], 2005年中国气象局又在全国下发了《中短期天气预报质量检验办法》 ①, 该办法中规定的各种检验方法主要针对单站和区域的天气预报质量, 是目前国内普遍使用的业务试行标准。国内科研人员近几年进行的一些相关研究[12-16], 基本上是对这些方法的应用和解释。宫春宁等[17]通过对内蒙古2003-2005年的预报质量评分, 曾指出现有的检验方法仍不能全面反映预报工作的质量状况和预报员的真实水平, 并对天气预报质量检验问题进行了讨论。国家气象信息中心近两年来对全国各省(区、市) 降水和气温预报产品进行晴雨(雪) 预报正确率和气温预报准确率检验和对比分析表明, 其评估结果基本上反映了我国天气预报的客观水平, 但另一方面, 由于我国幅员辽阔、各地天气气候特征差异明显的客观因素, 造成各地天气预报的难度存在较大差异, 采用晴雨(雪) 和气温预报正(准) 确率检验方法不能完全准确、客观反映各省(区、市) 降水和气温预报技术的能力和水平, 评分结果在不同地域间的可比性较差。针对上述情况, 本文对晴雨(雪) 和气温天气预报的检验方法进行了改进尝试和研究。

①中国气象局. 《关于下发中短期天气预报质量检验办法(试行) 的通知》(气发〔2005〕109号)

1 资料和基本概念 1.1 资料来源及处理

本文进行预报评分方法对比试验所用的资料包括两部分:每日通过9210通讯线路上传到国家气象信息中心的全国373个地市级城市天气预报产品②; 从国家气象信息中心实时库中获取的全国每日天气实况数据。全国天气预报产品取每日08: 00-08: 00 (北京时, 下同) 和20: 00-20: 00的0～24 h预报。

②中国气象局预测减灾司. 《关于传输城镇天气预报的通知》(气预函〔2006〕27号).

1.2 预报评分与预报准确率的区别

预报评分与预报准确率是两个不同概念。预报准确率反映预报与实况差别的客观情况。预报评分则反映预报员的技术水平, 既要体现预报与实况差别的客观情况, 也要体现天气变化程度不同对预报准确率的影响。

检验预报与实况差别的大小, 可以采用两种不同的标准:绝对标准和相对标准。绝对标准是指对于不同的站采用统一的固定阈值进行预报检验。绝对标准适用于预报准确率的统计。相对标准是指对于不同站不采用统一的固定阈值, 而是根据检验目的采用一定规则计算各自的阈值进行预报检验。与天气变化程度有关的相对标准适用于预报评分的统计。本文主要从预报评分角度对晴雨(雪) 和气温预报的质量检验方法的优劣进行讨论和对比。

2 晴雨(雪) 天气预报质量检验 2.1 现有预报检验方法

对于离散型预报量, 常用的预报检验方法包括预报正确率、预报成功率和预报技巧评分3种。其中预报正确率是目前晴雨(雪) 预报检验最常使用的检验方法, 也是本文分析研究的重点, 具体计算公式为

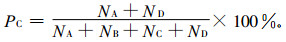
(1)

式(1) 中, NA为有降水预报正确站(次) 数, NB为空报站(次) 数, NC为漏报站(次) 数, ND为无降水预报正确的站(次) 数。

2.2 预报正确率影响因子分析

预报正确率简单实用、计算方便, 能在一定程度上反映晴雨(雪) 预报的优劣, 但它没有考虑降水概率对预报正确率的重要影响, 因而不能有效区别盲目预报或持续性预报造成的预报正确率异常偏高, 甚至会造成一些假象[18]。由式(1) 可看出, 预报正确率取决于NA和ND, 如果降水概率很小, 即使每天报无降水, 其预报正确率也会很高。同样, 如果降水概率很大, 即使每天报有降水, 其预报正确率也很高。所以, 预报正确率虽然是对预报和实况比较情况的客观反映, 但是对于降水概率差别很大的不同地区, 由于其预报技术难度差别很大, 用降水预报正确率作为标准进行预报评分并不适合。

2.3 与降水概率有关的错报减分法

充分考虑了降水概率对晴雨(雪) 预报评分的影响, 本文提出了与降水概率有关的错报减分评分法(简称错报减分法), 用于对晴雨(雪) 天气预报的评分, 试图尽可能减小降水概率对晴雨(雪) 预报检验的影响。对错报进行减分处理, 错报1次, 减1次分, 减分值随降水概率改变, 降水概率越接近50 %, 减分值越小, 降水概率越接近0或100 %, 减分值越大。这种思路实际上是根据不同地区晴雨(雪) 预报难度的不同, 对相同的预报结果在分数上进行了区分, 从而体现预报员的实际水平。

错报减分法的难点在于根据预报同时段历史资料计算的降水概率确定错报减分值的具体算法。预报正确率可以改写为

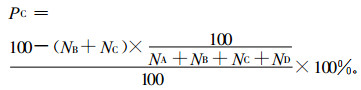
(2)

如果用k表示晴雨(雪) 预报为错报次数, 则k=NB+NC, 用d1表示错报对应的减分值, 则d1=100/(NA +NB+NC +ND)。式(2) 可表示为PC=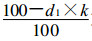×100 %。根据错报减分法的设计思路, 就是通过改变d1的算法, 确定新的减分值, 使其成为与降水概率相关的变量, 且满足两个基本条件: ①减分值随降水概率改变, 降水概率越接近50 %, 减分值越小, 降水概率越接近0或100 %, 减分值越大; ②全报对时得满分, 全报错时得零分或负分。

假定有n次预报, 其相应预报时段的历史统计资料中有降水出现为a次, 无降水为b次, 则n=a +b。如果用d表示错报时新的减分值, 用PF表示错报减分法得到的预报评分, 则可表示为

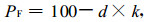
(3)
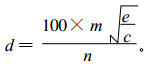
(4)

式(4) 中, c=(a +1)×(b +1), m为调幅参数, m越大, 减分值d的差别越小。

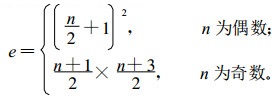
(5)

以上评分公式具有如下特点: ①当降水概率等于50 %时, d=d1, 预报评分PF等同于预报正确率PC, 即预报正确率是错报减分法在降水概率等于50 %的一种特例; ②当n确定时, a, b相差越多, c值越小, 表明降水概率越接近50 %, 减分值越小, 降水概率越接近0或100 %, 减分值越大; ③全报对时(k=0), 预报评分PF=100;如果全部报错时(k=n), 当降水概率等于50 %时, 预报评分PF=0, 当降水概率大于或小于50 %时, 预报评分小于0; ④降水次数a与无降水次数b在公式中的地位完全相同, 可以互换; ⑤调整调幅参数m的值, 可以改变减分值的幅度, 适当调整降水概率对评分的影响程度。

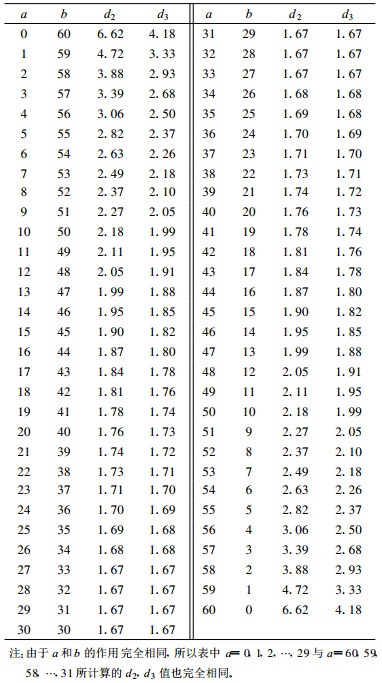
表 1显示了当预报次数为60次时, 利用式(4) 计算出的降水次数a和无降水次数b对应的减分值。可以看出, 表 1中减分值与降水次数的数据对应关系体现了错报减分法的设计思路, 降低了对持续性有降水或无降水天气做出正确预报的评分, 相对提高了对降水概率为50 %的天气做出正确预报的评分。

表 1 预报次数n=60时不同降水次数a或无降水次数b的减分值d(d2, d3分别为m=2, m=3时的计算值) Table 1 Relationship between the score-d and the different rainfall frequency (a or b) (d2 computed by m=2, d3 computed by m=3)

2.4 预报评分对比检验

错报减分法是否有效地消除或减小了降水概率对晴雨(雪) 预报评分的影响, 可以通过错报减分法的评分与降水概率的相关系数进行检验。利用全国373个城市每日08: 00-08: 00和20: 00-20: 00的0～24 h时晴雨(雪) 预报和相应气象站点实况资料对预报正确率(简称PC)、错报减分法(简称PF; m=2时, 简称PF1; m=3时, 简称PF2) 3种评分方法进行统计检验和比较。用3种方法分别对373个城市站点逐站计算2007年1, 4, 7, 10月的预报评分统计, 形成全国各月的站点无降水概率序列(此处用同时段实况资料代替历史实况资料计算降水概率) 和3个预报评分序列, 分别计算无降水概率序列和各预报评分序列数据的相关系数。计算结果如表 2所示。

表 2 各评分方法统计结果与单站无降水概率相关系数检验 Table 2 The correlation coefficient of comparing rainfall frequency with the forecast score of precipitation by different method

表 2的统计结果表明:从全国情况看, 在降水概率全国差异较大的1, 4, 10月PC评分与无降水概率表现为正相关, 而在全国降水概率普遍较大的7月, PC评分与无降水概率呈很弱的负相关; 而PF评分统计值与单站无降水概率在1, 4, 10月的相关很微弱, 在7月则与PC评分基本相当。显然, PF评分对于减少降水概率对晴雨(雪) 预报评分的影响有一定效果。

2.5 错报减分法的应用

错报减分法适用于月的晴雨(雪) 预报评分, 也可用于雨季等具有某种降水特点时段的晴雨(雪) 预报评分。需要注意的是, 由于1年中降水的时间分布一般很不均匀, 因此, 错报减分法不适合直接用于计算年的晴雨(雪) 预报评分, 年的晴雨(雪) 预报评分只能是12个月预报评分的平均值。另外, 错报减分法只适用于单站预报评分, 不直接应用于区域(多站点) 的总体评分, 区域总体评分可以通过计算单站评分的平均值获得。

3 气温预报质量检验 3.1 现有预报检验方法

气温天气预报, 通常指日最低和最高气温的预报, 属于连续性预报量。对于连续性预报量, 常用的预报检验方法包括平均绝对误差、均方根误差和预报准确率3种。其中, 预报准确率是目前最常使用的气温预报检验方法, 也是本研究的重点, 计算方法为

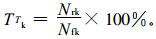
(6)

式(6) 中, Nrk为预报正确的次数, Nfk为预报的总次数。如果Fi为第i次气温(最低气温或最高气温) 预报值, Oi为第i次气温实况值, Tk为预报准确率阈值(通常取固定值1 ℃或2 ℃), 当|Fi-Oi|≤Tk, 为预报正确。

3.2 预报准确率影响因子分析

对全国城市最低、最高气温天气预报的评分进行分析发现, 以预报阈值取1 ℃(或2 ℃) 的气温预报准确率作为气温预报评分的标准, 其预报评分在不同程度上反映了各地的预报技术水平, 但对于气温日际变化不同的区域, 呈现有气温日际变化越大评分越低的趋势。也就是说, 影响预报准确率的因子除了预报技术水平以外, 还有气温日际变化这一因子。减小气温日际变化的因素对气温预报评分的影响, 以提高预报评分合理性, 可以通过改变气温预报准确率阈值来实现, 即将原来1 ℃(或2 ℃) 的固定值改变为与台站气温日际变化相关的一个相对标准值。本文研究提出了新的阈值(Tk) 的取值方法, 用于对气温预报的评分, 试图减小气温日际变化对气温预报检验的影响。

3.3 阈值Tk取值方法

新的气温预报准确率阈值Tk的取值方法采用与气温日际变化量值有关的指数函数方式计算, 简称指数阈值:

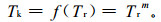
(7)

式(7) 中, Tr为气温日际变化绝对值的平均值, m是指数, 为调幅参数, 取值在0～1之间。

3.4 预报评分对比检验

本文取m=1, 2/3, 1/2, 1/3计算的4个阈值和两个固定阈值进行预报准确率评分对比检验, 分别用Tk1～Tk6表示6个阈值: Tk1=1, Tk2=2, Tk3=Tr, Tk4=Tr2/3, Tk5=Tr1/2, Tk6=Tr1/3。利用实况资料, 分别计算出2007年1, 4, 7, 10月全国373个城市单站最低、最高气温的Tk3, Tk4, Tk5, Tk6值。鉴于气温预报的精确度为1 ℃, 因而计算中设定Tk3～Tk6的最小值为1 ℃(即将小于1 ℃的Tk3～Tk6修正为1 ℃)。

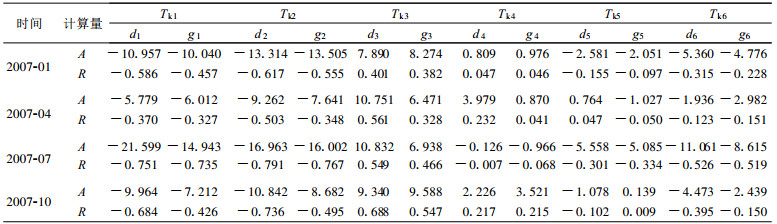
用Tk1～Tk6共6个阈值分别计算出2007年1, 4, 7, 10月全国373个城市单站每日08: 00-08: 00和20: 00-20: 00的0～24 h最低气温预报评分。然后, 分别计算最低气温预报评分序列与各站逐月日际变化平均值(Tr) 序列的直线回归斜率A和相关系数R。同样方法计算出单站最高气温预报评分与最高气温日际变化的直线回归斜率A和相关系数R。计算结果见表 3(最低、最高气温的计算结果分别用d1～d6和g1～g6表示)。

表 3 不同阈值下最低、最高气温预报评分结果与最低、最高气温日际变化平均值直线回归斜率(A) 和相关系数(R) Table 3 The linear regression coeff icient (A) and the correlation coefficient (R) between the daily changing of the air temperature and the forecast score of daily minimum/maximum temperature by adopting the different standard value as the threshold

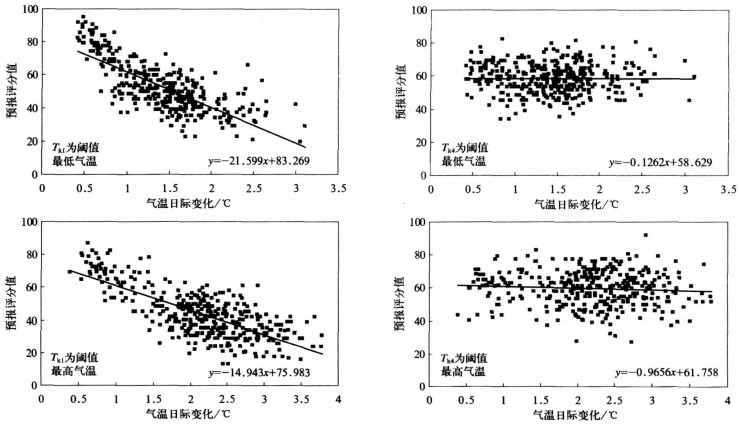
表 3数据表明, 以1 ℃或2 ℃绝对标准值(Tk1, Tk2) 作为阈值, 预报评分值与气温日际变化呈负相关, 直线回归斜率绝对值为5. 779～21. 599, 相关系数为-0. 327～-0. 791, 气温日际变化偏小则评分值偏高的趋势比较明显; 以日际变化绝对值的平均值(Tk3) 作为阈值, 正好与1 ℃或2 ℃绝对标准值作为阈值的效果相反, 预报评分值与气温日际变化呈正相关, 直线回归斜率为6. 471～10. 832, 相关系数为0. 328～0. 688, 气温日际变化偏小评分值偏低的趋势比较明显; 以m=2/3, 1/2计算的阈值(Tk4, Tk5), 预报评分值与气温日际变化的直线回归斜率绝对值明显减小, 在0. 126～5. 558之间, 相关系数绝对值也明显减小, 大多在0. 150以下, 也就是说, 预报评分值随气温日际变化值的变化相对于阈值取1 ℃或2 ℃计算的预报准确率随气温日际变化值的变化小得多。以气温日际变化相对较大的7月为例, 从Tk1和Tk4作为阈值时最低、最高气温预报评分值和气温日际变化值之间的线性趋势(图 1) 可以明显看出这种差别。

图 1. 全国373站2007年7月最低、最高气温预报评分值和气温日际变化之间的线性趋势 Fig 1. Comparison of the daily changing of air temperature and the forecast scores of daily minimum/ maximum temperature of 373 stations over China in July 2007

另外, 结果显示:以1 ℃和2 ℃绝对标准值(Tk1, Tk2) 作为阈值的评分值差别比较大, 以m=2/3, 1/2计算的阈值(Tk4, Tk5), 其评分值整体上介于以1 ℃和2 ℃绝对标准值(Tk1, Tk2) 作为阈值的评分值之间, 全国最低评分和最高评分的差值低于Tk1统计结果, 与Tk2统计结果基本相当, 评分结果相对更为合理。

显然, 以m=2/3, 1/2计算的阈值(Tk4, Tk5) 进行气温预报准确率的评分, 可以有效减少气温日际变化不同对预报评分的影响, 评分结果也更为合理。

3.5 指数阈值评分的应用

m=2/3, 1/2的指数阈值评分适用于月的气温预报评分, 也可用于某些特定时段的气温预报评分。同样需要注意的是, 由于1年中日最低、最高气温的日际变化在不同的季节差别很大, 因此指数阈值评分不适合直接用来计算年的气温预报评分, 年的气温预报评分只能是12个月的预报评分的平均值。另外, 指数阈值评分也只适用于单站预报评分, 区域(多站点) 总体评分可以通过计算单站评分的平均值获得。

4 小结

1) 降水概率对晴雨(雪) 预报评分具有重要影响。不考虑降水概率的晴雨(雪) 预报正确率评分(PC评分) 简单实用, 但其评分结果与单站无降水频率在降水概率全国差异较大的多数月份呈正相关, 具有无降水频率越大评分越高的趋势。本研究提出的与降水概率有关的错报减分法(PF评分), 其评分值与单站无降水频率在各月的相关都很微弱, 对于减少降水概率对晴雨(雪) 预报评分的影响具有一定效果。另外, 错报减分法实际是对预报正确率评分的扩展, 当降水概率等于50 %时, 预报评分PF等同于预报正确率PC, 即预报正确率是错报减分法在降水概率等于50 %的一种特例。

2) 气温日际变化对气温预报评分具有重要影响。采用全国统一固定阈值的气温预报准确率评分, 其预报评分在不同程度上反映了各地的预报技术水平, 但对于气温日际变化不同的区域, 评分结果与气温日际变化呈明显负相关, 气温日际变化偏小则评分值偏高的趋势比较明显。采用与气温日际变化有关的指数阈值评分, 在指数m=2/3, 1/2时, 可以有效减少气温日际变化不同对预报评分的影响, 其评分结果整体上介于以1 ℃和2 ℃绝对标准值作为阈值的评分值之间, 全国最低评分和最高评分的差值低于1 ℃统计结果, 与2 ℃统计结果基本相当, 评分结果相对更为合理。

科学合理的预报评分方法可以比较客观地反映不同地区天气预报工作的能力和水平, 有助于推动各地区预报工作的发展。本研究对晴雨(雪) 和气温预报检验方法的改进进行了初步的探索, 从评分的对比结果看, 效果比较理想, 在天气预报质量检验和评估业务中具有一定的应用推广价值。

参考文献
[1] 李泽椿, 毕宝贵, 朱彤, 等. 近30年中国天气预报业务进展. 气象, 2004, 30, (12): 4–10.
[2] 章国材. 预报员在未来天气预报中的作用探讨. 气象, 2004, 30, (7): 8–11.
[3] 汤懋苍. 短期天气预报与短期气候预测发展道路的对比思索. 干旱气象, 2004, 22, (1): 57–64.
[4] 矫梅燕, 龚建东, 周兵, 等. 天气预报的业务技术进展. 应用气象学报, 2006, 17, (5): 594–601.
[5] 矫梅燕. 关于提高天气预报准确率的几个问题. 气象, 2007, 33, (11): 3–8.
[6] 伍荣生, 谈哲敏, 王元. 我国业务天气预报发展的若干问题思考. 气象科学, 2007, 27, (1): 112–118.
[7] 汪高明, 张火平. 天气预报质量评估监控系统的研究与开发. 湖北气象, 2004, (2): 20–22.
[8] 李建明, 王晖, 郝家学, 等. 中短期天气预报质量检验系统. 山东气象, 2006, 26, (3): 18–20.
[9] 黄阁, 韩秀君, 盛永. 辽宁省分县指导预报评分检验系统. 气象与环境学报, 2007, 23, (4): 33–38.
[10] 栾东红, 姜延浩, 黄本锋, 等. 完善县级气象台站短期天气预报质量评分办法的初探. 山东气象, 2006, 26, (4): 52–54.
[11] 黄海洪, 郑凤琴, 孙崇智. 一种新型降水预报评分方法. 气象, 2004, 30, (9): 35–38.
[12] 邓雪娇, 胡胜, 闫敬华. 主客观天气预报质量对比分析. 应用气象学报, 2003, 14, (6): 729–738.
[13] 王雨. 2003年主汛期及淮河强降水过程中外数值模式降水预报检验. 天气与气候, 2004, (1): 78–87.
[14] 王雨, 闫之辉. 2004年汛期(5-9月) 主客观降水预报检验. 热带气象学报, 2006, 22, (4): 331–339.
[15] 周兵, 赵翠光, 赵声蓉. 多模式集合预报技术及其分析与检验. 应用气象学报, 2006, 17, (增刊): 104–109.
[16] 漆梁波, 曹晓岗, 夏立, 等. 上海区域要素客观预报方法效果检验. 气象, 2007, 33, (9): 9–18.
[17] 宫春宁, 李一平, 付丽娟. 天气预报质量及影响因素的探讨. 内蒙古气象, 2007, (6): 9–11.
[18] 余剑莉. 统计天气预报. 北京: 气象出版社, 1994.