在海洋大气边界层中, 存在着不同层高的大气折射陷获层, 使部分电磁波被陷获在一定厚度的大气边界层内传播, 这种现象称为大气波导。由于大气波导的存在, 改变了电磁波的传播特征, 使电磁波能够克服地球曲率的限制, 实现超远距离传播, 使雷达等电子装备具有超视距探测的能力。
大气波导一般分为蒸发波导、表面波导、抬升波导[1]。对海上电子装备影响最大的是海上蒸发波导, 它普遍存在于我国周边海区, 特别在我国低纬度热带海区可利用的蒸发波导出现概率约为80%, 中高纬度海区约为40%~50%。国外资料显示, 美、俄已在20世纪50, 60年代开展了波导现象及其在军事上的应用研究[2]。美国的Paulus-Jeske模型[3] (简称PJ模型) 是早期最成功、并被广泛使用的蒸发波导模型, 1978年被美国海军用作业务化预报模型, 并且嵌入美海军的高级折射效果预报系统AREPS, 用以评估预报海上电磁波传播, 一直延用至今。此外, 还有LKB蒸发波导模型[4], Babin蒸发波导模型[5], Naval Postgraduate School模型(NPS模型)[6], 欧洲中尺度预报系统的Musson-Genon-Gauthier-Bruth模型(MGB模型)[5]等。国内大气波导方面的研究开展较晚, 但也取得了一些成果, 刘成果等对PJ模型进行了部分改进, 建立基于伪折射率概念的蒸发波导模型[7]。戴福山[8]在Babin模型的基础上, 提出了局地相似蒸发波导模型。各种模型建立的目的在于更加准确地提供大气波导特征量, 为波导环境下的电磁波传播评估提供输入。
但是, 目前在波导诊断模型的研究中仍然存在不足, 主要表现为:经验关系函数应用多, 诊断精度难以保障。例如PJ, MGB模型, 主要是依赖了Richardson数和Obukhov长度之间的经验关系, 而且许多经验关系是通过陆上试验总结得出的, 对于下垫面是海洋的情况试验较少; 低风速条件下Monin-Obukhov相似理论的实用性问题; 海水盐度对于水汽压的影响; 蒸发波导高度微分迭代计算的收敛性问题。本文在借鉴综合国外研究的基础上避免和克服上述不足, 并通过系统的海上试验进一步阐明基于通量算法的蒸发波导诊断模型效果。
1 基于通量算法的蒸发波导诊断模型由于蒸发波导常发生于近海面层, 因此MoninObukhov相似理论成为处理这类问题的基础。本文建立的基于通量算法的蒸发波导模型 (简称Flux模型)将相似理论与通量算法结合, 首先求得各气象要素垂直廓线分布, 进而得到修正折射率廓线, 根据修正折射率最小值对应的高度, 确定波导高度。
1.1 确定各气象要素廓线长期开展的 TOGA COARE[9-11]调查所改进的海气通量计算方法已被广泛使用[12-14], 算法所用到的函数关系均来自于大洋试验。本文借鉴TOGA COARE Bulk Model 3.0与Monin-Obukhov相似理论, 确定表层的风速、温度、比湿的特征尺度u*, θ*, q*。
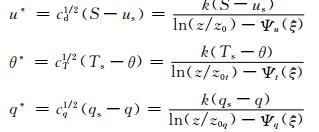
|
(1) |
式(1)中, 风应力、感热、潜热的输送系数cd, cT, cq采用Geernaert等[15]给出的形式; k=0.4, z为垂直高度; S, θ, q为z高度处的水平风速、气温和比湿; us是近海面的风场, 一般取为零; T s是海表水温; qs是海面通过饱和状态修正的比湿; z0, z0t, z0q分别是风速、温度和比湿的粗糙度; Ψu, Ψt, Ψ q是稳定度ξ的函数, 称为普适函数。ξ, z0, z0t, z0q, Ψu, Ψt, Ψq采用文献[10]的方法确定。如果已知某一高度z处的气象要素数据, 通过式(1)迭代计算确定u*, q*, θ*, 从而得到温度、比湿廓线。同时, 利用大气静力学方程和理想气体方程可得到气压廓线。
1.2 拓展Monin-Obukhov相似理论经典的Monin-Obukhov相似理论仅适用于u*不为零的情况, 然而在局地对流情况下, 即使水平平均矢量风的模为零, 也会由于垂直对流活动引起水平运动。因此, 本文借鉴Godfrey等[16]的研究成果拓展相似理论的适用范围, 引入阵性风速项wg, 修正了新的地面风速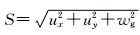

|
(2) |
式(2)中, w*是自由对流速度特征尺度; β为经验常数, 一般取1.25。Fb为浮力通量项, 代表湍流的波动性。zi为对流层高度, 这里取600 m, Tv为虚温。
1.3 确定蒸发波导高度已知温度、比湿、气压廓线, 根据无简化近似的大气折射指数N的计算式(3)[17]和大气修正折射率式(4)得到修正折射率M的廓线, 则廓线上M的最小值对应的高度即为蒸发波导高度。

|
(3) |
式(3)中, P, e分别是总大气压和水汽分压, 单位为hPa; T是气温, 单位为K。
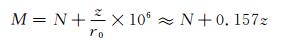
|
(4) |
式(4)中, r0是地球半径, 单位为m; z是高度, 单位为m。
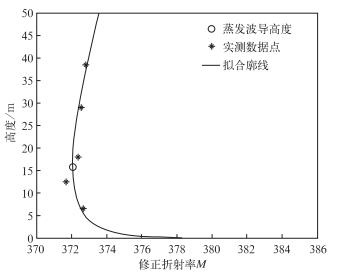
2 模型实测对比分析利用2002年5月平潭岛铁塔数据, 进行实测数据拟合, 建立模型实测对比标准廓线(如图 1所示)。观测铁塔高约40 m, 分5层布设传感器, 连续观测大气压、大气温度、风速、风向和相对湿度等相关要素, 各层距离平均海面高度分别为6.5 m, 12.5 m, 18 m, 29 m和38 m。本文采用Babin[5]提出的对数最小二乘法拟合确定M廓线。

|
(5) |
式(5)中, z′为已知常数, 取0.001; A, B, C为待定系数, 通过最小二乘法拟合确定。函数确定后从0到50 m, 每间隔0.1 m计算M值, M最小值点对应的高度为蒸发波导高度。
|
|
| 图 1. 实测数据拟合廓线图 Fig 1. Profile of least squares log-linear curve fit to the tower data | |
2.1 波导高度散点图对比分析
选取2002年5月26-27日平潭岛铁塔10 min平均的82组实测数据, 利用曲线拟合计算实测蒸发波导高度, 与模型计算的高度进行对比。
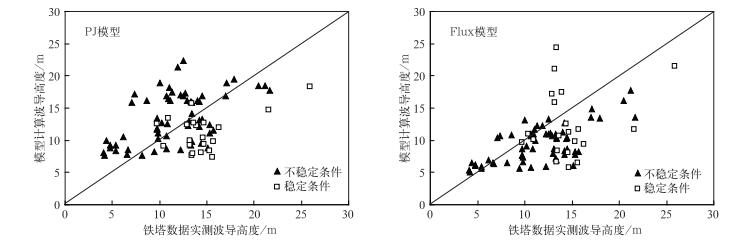
图 2显示了不同稳定度条件下两模型的评估效果, 总体上讲, Flux模型与实测结果较为接近, 明显优于PJ模型。另外, 两模型在稳定条件下的计算精度低于不稳定条件。
|
|
| 图 2. 模型计算蒸发波导高度与实测高度对比散点图 Fig 2. Plot of PJ and Flux Model duct height versus boatde-rived duct height for the tower data | |
2.2 关于修正折射率M的对比分析
为了进一步评估模型的优劣及模型间的差异, 利用5月26日2 min平均实测数据, 针对3种关于修正折射率M的评估标准进行对比分析。
标准1 平均M梯度比较, 即计算铁塔相邻高度的M梯度以至整个铁塔高度。模型也进行相应的类似计算, 求铁塔实测M梯度均值与模型计算的均方根误差。计算得到Flux模型的均方根误差为0.0377, PJ模型的均方根误差为0.0799, 可以看出, Flux模型计算得到的修正折射率误差小于PJ模型。
标准2 M值的均方根偏差, 即计算铁塔5个高度上修正折射率平均值


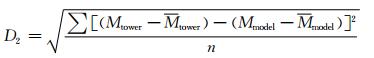
|
(6) |
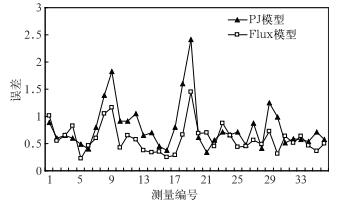
|
|
| 图 3. 标准2的计算结果 Fig 3. The result of Standard 2 | |
由图 3可见, 除在个别点以外, Flux模型的偏差量明显比PJ模型小。
标准3 比较M廓线, 主要是通过铁塔数据的拟合的M廓线与模型计算的M廓线比较。采用对应高度上相同间隔的小段(如0.2 m), 计算这一小段上的M梯度, 累加M梯度至整个廓线高度, 求均方根偏差。
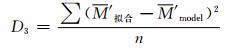
|
(7) |
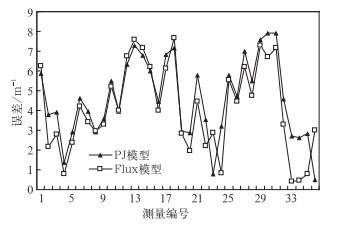
模型计算廓线的修正折射率M梯度与铁塔实测值的误差如图 4所示, Flux模型总体上偏差量相对较小, 仅有7次误差量大于PJ模型, 但偏差距离不大。
|
|
| 图 4. 标准3计算结果 Fig 4. The result of Standard 3 | |
2.3 不同稳定度条件下的M廓线对比
考虑到模型在ξ≥0和ξ < 0条件下使用的普适函数不同, M廓线的计算也有不同, 所以下文按照不同的稳定度条件进行M廓线的对比。
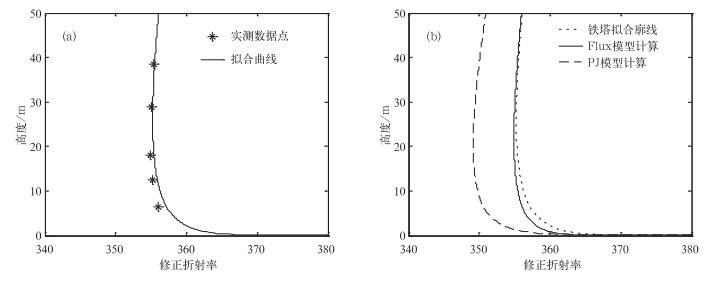
①稳定条件 2002年5月26日12:00(北京时, 下同)实测数据:大气压为1011 hPa、大气温度为23.524 ℃、风速为6.3 m/s、相对湿度为72%、水温为22.7 ℃。图 5为稳定条件下铁塔、模型的M廓线图。
|
|
| 图 5. 稳定条件下铁塔(a)、模型(b)的M廓线 Fig 5. Plot of modified refractivity profile as deter mined by the tow er data(a)for comparison with the models(b)from Ping tan Island in the stable cases | |
经过计算, Flux模型的误差率为0.8212 m -1, 而PJ模型的误差率为3.2192 m -1。PJ模型误差较大。从图 5可看出, 图 5a铁塔实测资料拟合情况较好。图 5b中Flux廓线、PJ廓线曲率与拟合曲线相似, 但PJ廓线在相同高度上的M值与拟合曲线相差较大, 所以不能与拟合曲线完全吻合, 存在一定的水平偏差量ΔM, 这与标准2的结论一致。
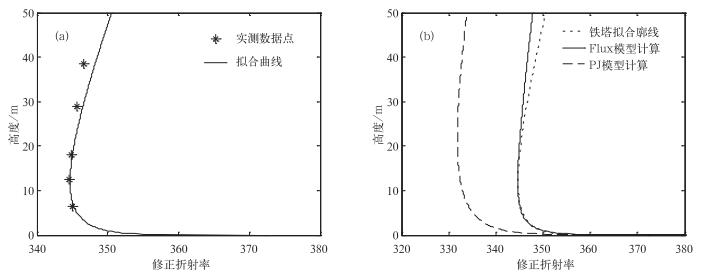
②不稳定条件 2002年5月26日02 : 00实测数据:大气压为1010.5 hPa、大气温度为22.7 ℃、风速为4.3 m/s、相对湿度为79%、水温23.1 ℃。图 6为不稳定条件下铁塔、模型的M廓线图。
经过计算, Flux模型的偏差为2.3946 m -1, 而PJ模型的结果为2.9149 m -1。从图 6中看出, 根据5个测量高度实测值拟合的曲线情况较好, PJ模型计算的廓线曲率与拟合曲线相似, 但在相同高度上的M值与拟合曲线仍然存在水平偏差量ΔM, 仅在1 m以下很小的高度上M值相差较小。
|
|
| 图 6. 不稳定条件下铁塔(a)、模型(b)的M廓线 Fig 6. As in Fig. 5, but for the unstable cases | |
对Flux模型、PJ模型多项对比显示, 总体上Flux模型要优于PJ模型。但值得注意的是, 蒸发波导高度虽然是一个十分关键的代表量, 但不能完全代表大气环境状况。而M廓线不仅包含了蒸发波导高度的信息, 而且其曲率形态表征了整层的大气环境情况, 这对于海上电磁传播评估尤为重要。同时, 发现当模型评估的蒸发波导高度准确时, M廓线未必和实际情况吻合, 这方面Flux模型略优于PJ模型。
3 雷达探测配合试验2002年6月1日在平潭岛海域进行了大气波导环境监测与RM-1070导航雷达探测配合试验[14-15]。试验过程中使用了监测铁塔、系留汽艇等手段, 不仅监测到蒸发波导, 还监测了表面波导和抬升波导等异常折射条件。这里主要通过蒸发波导环境下雷达电磁波传播特征分析、探测威力的评估进一步验证模型的准确性。
利用6月1日23 : 00观测数据:少云, 东北风5~6级, 能见度约5 n mile, 浪高1 m, 气温为23.9 ℃, 水温为24.4 ℃, 气压为1006.8 hPa, 风速为7.6 m/s, 湿度为83%进行试验验证。此时为落潮时, 因此天线高度订正为16.2 m, 探测目标雷达反射面积约为20000 m 2, 慢起伏, 目标高度10 m, 雷达正常理论视距为15.9 n mile(约29.4 km)。实际雷达可观测到148°方向62.9 km的海上目标, 由此可见雷达已发生超视距。
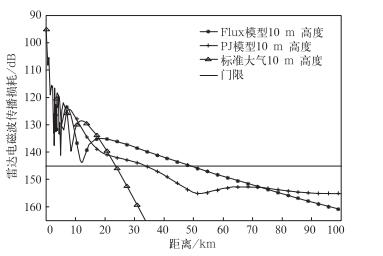
应用电磁波传播PEM模型[18]利用PJ模型、Flux模型诊断的蒸发波导环境数据, 计算雷达电磁波的传播损耗, 评估雷达最大探测距离。图 7显示的是10 m高度上的单程传播损耗随距离的变化。在满足探测概率0.9, 虚警概率10-6条件下, 计算雷达能够探测到目标所需的最大单程传播损耗为145.1 dB, 这里称之为单程传播损耗的门限, 传播损耗小于这一门限表示目标能被探测到。
|
|
| 图 7. 雷达电磁波单程传播损耗随距离分布 Fig 7. Plot of the radar wave one-way propagation loss distribution | |
依据图 7可以预测雷达的最大作用距离, 如果当时为标准大气环境, 探测距离仅为23 km, 而实际看到了62.9 km的目标, 显然说明海上存在大气波导。利用Flux模型评估的最大探测距离为49 km, 误差为22.1%;利用PJ模型评估的最大探测距离为34 km, 误差45.9%, 由此可见, Flux模型更加接近实况。
4 结论与讨论基于TOGA COARE 3.0通量算法的蒸发波导模型, 考虑了阵风项, 理论上更加完备, 能够提供更为精确的蒸发波导高度信息。其次, 通过波导高度、廓线形态的比较分析, Flux模型与实际吻合较好, 特别是在不稳定条件下效果更好, 并且能够为海上雷达性能的评估应用提供更为准确的波导环境诊断信息。
然而, 由于海上试验数据有限, 还需进一步开展更加全面的检验性试验。此外, 基于通量算法的蒸发波导模型依据Monin-Obukov近地层相似理论, 这就无法避免水平均一的假设。由于不同海域气象要素的水平分布特征不同, 模型的准确程度也就不同。因此, 应该在不同海域开展海上试验, 结合我国各海域不同大气水文特点, 尽量减少模型中的经验系数和假设, 增强模型适用性。
| [1] | 姚展予, 赵柏林, 李万彪, 等. 大气波导特征分析及其对电磁波传播的影响. 气象学报, 2000, 58, (5): 605–616. |
| [2] | Hitney H V, Richter J H, Integrated Refractive Effects Prediction System (IRE PS). Naval Engineers Journal, 1976, 88, (2): 257–262. DOI:10.1111/nej.1976.88.issue-2 |
| [3] | Paulus R A, Practical Application of the IREPSE vaporation Duct Model. Naval Ocean System Center Technical Report, 1984. |
| [4] | Liu W T, Katsaros K B, Businger J A, Bulk parameterization of air-sea exchanges of heat and water vapor including the molecular constraints at the interface. J Atmos Sci, 1979, 36: 1722–1735. DOI:10.1175/1520-0469(1979)036<1722:BPOASE>2.0.CO;2 |
| [5] | Babin S M, A New Model of the Oceanic Evaporation Duct and Its Comparison with Current Models. University of Maryland, 1996. |
| [6] | Newton D A, COAMPS Modeled Surface Layer Refractivity in the Roughness and Evaporation Duct Experiment 2001. Naval Postgraduate School, 2003. |
| [7] | 刘成果, 黄际英, 江成荫, 等. 用伪折射率和相似理论计算海上蒸发波导剖面. 电子学报, 2001, 29, (7): 970–972. |
| [8] | 戴福山. 大气波导及其军事应用. 北京: 解放军出版社, 2002. |
| [9] | Fairall C W, Hare J E, Edson J B, et al. Bulk parameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean Response Experiment. J Geophys Res, 1996: 3747–3764. |
| [10] | Fairall C W, Bradley E F, Measurement and parameterization of the air-sea gas transfer. Bound-Layer Meteor, 2000, 96: 63–105. |
| [11] | Fairall C W, Bradley E F, Bulk parameterization of air-sea fluxes:Updates and verification for the COARE algorithm. J Climate, 2003, 2: 571–592. |
| [12] | 阎俊岳. 中国邻海海-气热量、水汽通量计算和分析. 应用气象学报, 1999, 10, (1): 9–19. |
| [13] | 姚华栋, 任雪娟, 马开玉. 1998年南海季风试验期间海-气通量的估算. 应用气象学报, 2003, 14, (1): 87–92. |
| [14] | 姚华栋, 李骥, 丁一汇. TOGA-COARE IOP海表通量估算. 气象学报, 1996, 54, (6): 693–708. |
| [15] | Geernaert G L, Plan W J, Surface Waves and Fluxes. Boston: Kluwer Academic Publishers, 1990. |
| [16] | Godfrey J S, Beljaars A C M, On the turbulent fluxes of buoyancy, heat, and moisture at the air-sea interface at low wind speeds. J Geophys Res, 1991, 96: 22043–22048. DOI:10.1029/91JC02015 |
| [17] | Bean B R, Dutton E J, Radio Meteorology. New York: Dover Publications, 1968. |
| [18] | 黄小毛, 张永刚, 唐海川, 等. 大气波导对雷达异常探测影响的评估与试验分析. 电子学报, 2006, 34, (4): 722–725. |
 2009, 20 (5): 628-633
2009, 20 (5): 628-633

