2. 海军海洋水文气象中心, 北京 100073
2. Marine Hydrometeorologic Center, Bei jing 100073
天气过程中, 云内部微物理特征的演变对认识降水的形成、发展、消亡规律有重要作用。水凝物热力学相态作为主要的云微物理特征之一, 在人工影响天气、飞机积冰等研究领域有十分重要的地位, 其在降水过程中的演变一直受到广泛关注, 但探测手段缺乏也一直制约着这方面研究的开展。近年来, 随着双偏振技术在气象雷达上的逐步应用, 通过雷达探测反演云粒子相态成为可能。双偏振雷达可提供更多的雷达参量, 包括水平极化时测得的反射率因子 (Zhh)、垂直极化时测得的反射率因子 (Zvv)、差分反射率 (Zdr)、差示传播相移 (Φdp)、差示传播相位常数 (Kdp)、零滞后相关系数 (ρhv(0)) 和线性退偏比 (LDR) 等, 这些参量对降水粒子的大小、排列方式、密度、形状、空间取向、介电常数等特征有着不同的敏感度。利用这些参量就可以对降水粒子的相态进行反演, 在此方面的研究国内外已取得不少成果[1-8], 逐步形成了应用较广的模糊逻辑算法[9-18], 但在这些已有研究中, 大都仅对一次雷达探测数据进行分析, 利用连续的多次探测数据, 对天气演变过程中云粒子相态变化情况进行分析较少。
本文针对发展较为稳定的层状云, 联合利用双偏振雷达探测量和温度廓线数据, 建立了基于模糊逻辑技术的云粒子相态反演算法, 并利用连续的雷达RHI探测数据对一次层状云降水过程中水凝物相态演变进行了分析。
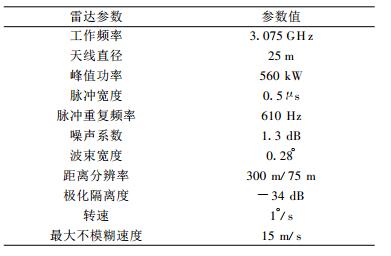
1 资料介绍本文所使用的雷达数据来自英国的CAMRa(Chilbolton Advanced Meteorological Radar)雷达 (http:∥www.met.rdg.ac.uk/radar/), CAMRa雷达位于英国南部的Chilbolton (51.43700°N, 1.14450°W), 频率3. 075 GHz, 具备双偏振能力, 部分参数如表 1所示。雷达数据时间为2003年6月6日。
|
|
表 1 CAMRa雷达性能 Table 1 CAMRa characteristics |
本文所使用的常规观测资料来自全球探空数据(RAOBs)3743号观测站 (51.20000°N, 1.80000°W) 的温度廓线数据, 此数据与雷达资料在空间上虽然不完全一致, 但对结构稳定的云层来说这两点距离已很接近, 同时本文的算法中并没有使用全部温度廓线信息, 只是使用它来确定几个特定温度对应的高度, 如0℃,-40℃等, 考虑到在雷达的探测路径上得到每一点的温度信息并不现实, 所以本文的算法中做了如下假设:对于发展较为稳定的云层, 特定等温层高度在雷达探测范围内保持不变。
2 算法描述及反演参量的选取参考Liu等[13]的研究成果, 本文使用了模糊逻辑分类法, 算法包括模糊化、规则推导、汇总和退模糊4部分[17]。
在云相态的反演中, 温度廓线有重要的参考意义, 探空数据提供了不同高度层的温度数据, 而温度是云滴呈现不同相态的决定性因素之一, 在温度小于-40℃时, 云中只存在冰相粒子, 在温度大于0℃时, 冰相粒子开始融化, 所以云中多为液态粒子, 而在-40~0℃之间, 就可能有冰相和混合相以及过冷的液态水等相态存在。由于在大气垂直分布中, 一般情况下, 温度随高度增加而递减, 所以在应用中将温度换算成对应的高度层, 而且仅使用了0℃和-40℃所对应的高度层 (分别记为h 0和h1)。
CAMRa雷达具有很高的敏感度和很窄的波束宽度, 在本文中其水平反射率因子Zhh用来对云及降水区域进行界定, 认为Zhh小于一定阈值的回波区域为非气象回波区。由于Zhh同单位体积内粒子总后向散射截面积 (粒子大小) 以及粒子的介电常数有关, 所以Zhh也用来对云相态进行判断, 例如, 对于CAMRa雷达, 当Zhh大于50 dBz时, 认为是强的降雨或大的冰雹。
线性退偏比LDR是接收到的正交极化分量与同极化分量比值的对数值。对于水平极化波, 球形粒子和轴对称粒子将会返回相同极化的回波, 趋近于-∞。LDR与粒子的形状、形状的不规则性、热力学相态、介电常数和在偏振平面上的倾斜角有关。在实际的云相态反演中, LDR也起重要参考作用。
差分反射率Zdr与粒子的大小和椭率有关, 它直接反映了粒子的形状和大小, 进而据此可以判断云粒子的相态, 这是因为冰晶粒子多为不规则形状, 而小的云滴往往具有较规则的球形。同时, 由于大量的大尺度粒子能够产生大的反射率因子, 所以它们也能严重影响LDR。例如, 大雨或冰雹也会产生大的Zdr, 所以结合温度的观测, 利用Zdr可以对云滴相态进行初步判断。
3 成员函数的选取参考已有研究成果, 本文选用Beta函数作为成员函数, 其表达式为:
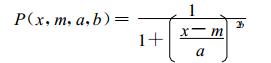
|
((1)) |
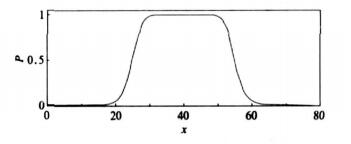
式 (1) 中, m, a, b为形状参数, x为输入变量, P为输出变量。Beta函数的形状是以x=m为对称轴的类梯形形式 (图 1), 其边角过渡平滑, 当x=m时, P取最大值1, 当x=m±a时, P=0. 5, 最小值趋向0;参数b代表了函数的陡峭程度, b越大函数越陡峭, 其典型的形状如图 1所示, 其中m=40, a=15, b=5。
|
|
| 图 1. Beta函数示意图 Fig 1. The shape of Beta function | |
不同相态的降水粒子与双偏振雷达的每个探测量都有一种对应关系, 例如, 大的冰雹粒子总与较大的雷达反射率相对应, 而小的云滴粒子产生小的反射率值, 不规则的大冰晶会产生大的差分反射率等。Beta函数可描述相态与雷达量之间的这种对应关系, 对应不同的雷达探测量x, 函数值P(x) 表示当雷达探测量取值为x时, 对应某种相态的合理程度 (或概率), P(x)=1表示对应某种粒子相态的概率最大, P(x) 趋向于0则不可能出现此种相态的粒子, 介于0~1之间的函数值表示一种模糊的不确定的对应关系, 值越大, 对应关系越强。例如, 当雷达反射率因子取值在30~50 dBz之间时, 相应的粒子相态为大雨滴是完全可信的, 而对于小云滴则认为是不可能的, 即对于雷达反射率因子, 此时相态大雨滴的成员函数为1, 相态小云滴的成员函数为0。
不同相态成员函数的建立基于其与雷达探测量之间的经验取值对应关系, 近年来已有大量研究探讨了双偏振雷达探测量与不同粒子相态的对应关系, 例如, Straka等[14]总结给出了大量的不同相态与不同雷达探测量间的阈值关系。
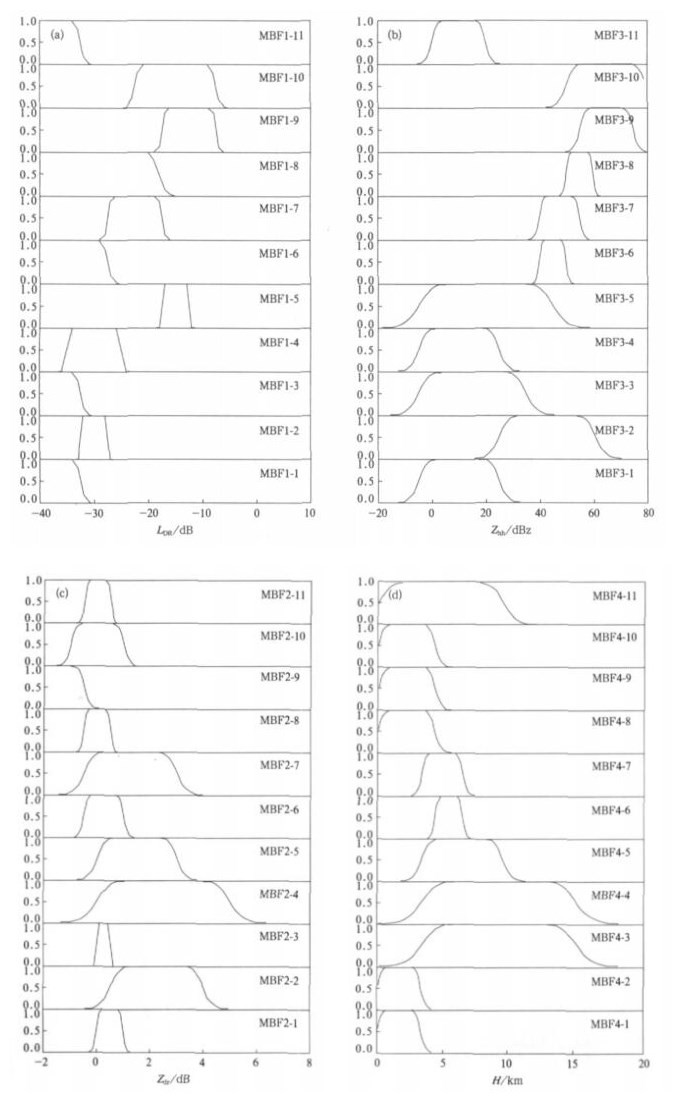
Liu等[13]利用S波段双偏振雷达建立了基于模糊逻辑的云相态反演算法, 其成员函数所用到的阈值关系是以机载实测数据为真值, 采用人工神经网络方法确定的。本文参考其研究成果, 建立了不同相态的成员函数, 具体参数见表 2, 其中所有成员函数中参数b都取为5, 图 2a~2d给出了相应函数的形状, 其中图 2d为h 0=3. 3 km, h1=9. 4 km时的高度成员函数, 这两个值分别代表了温度0℃和-40℃对应高度, 是通过RAOBs温度廓线 (图略) 得出的。其中的文字MBFi-j表示参量i对应相态j的成员函数 (membership function), i从1到4依次对应参量LDR, Zdr, Zhh和高度H, j从1到11依次对应相态毛毛雨、雨、低密度干冰晶、高密度干冰晶、湿冰晶、干霰、湿霰、小冰雹、大冰雹、雨夹雪和液态云滴。
|
|
表 2 4个输入参量对应10种相态的成员函数参数 Table 2 Membership function values of 4 input variables for 10 types of hydrometeors |
|
|
| 图 2. 各参量对应不同相态的成员函数示意图 (a)LDR, (b)Zhh, (c)Zdr, (d)H Fig 2. Membership functions of 4 input variables for its 10 fuzzy sets (a)LDR, (b)Zhh, (c)Zdr, (d)H | |
4 反演结果及分析
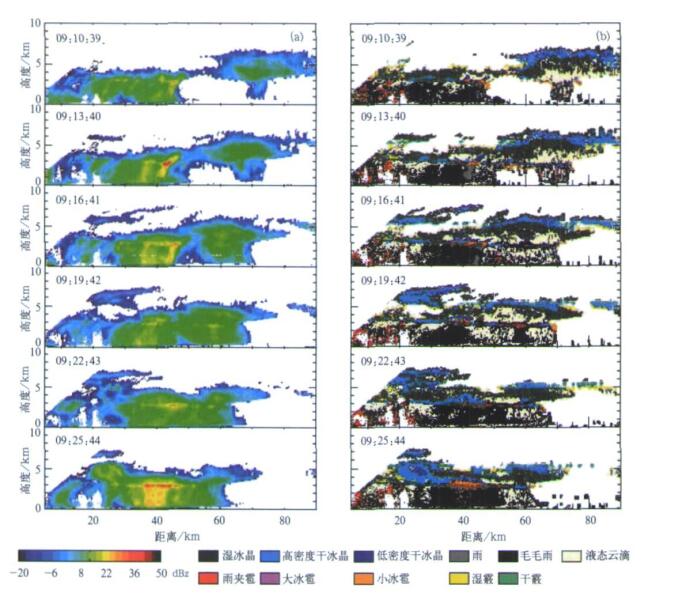
2003年6月6日09:10:39-09:49:52 (世界时,下同) 雷达做RHI扫描, 方位角为330°, 每181s进行一次扫描, 从雷达回波图中可以看出这是一次层状云降水逐步发展并消亡的过程, 利用其反射率因子图像可将其划分为发展、成熟、消亡3个阶段, 时间跨度依次为09:10:39 -09:25:44,09:28:45-09:34:47和09:37:48-09:49:52。针对3个阶段, 利用LDR, Zdr, Zhh和温度廓线数据, 使用模糊逻辑算法对水凝物相态进行反演, 图 3~5依次给出了3个阶段的雷达反射率因子和相态反演结果图。
|
|
| 图 3. 发展阶段的雷达反射率因子 (a) 和相态分类结果 (b) Fig 3. CAMRa Zhh(a) and classification results (b) during initial phase | |
|
|
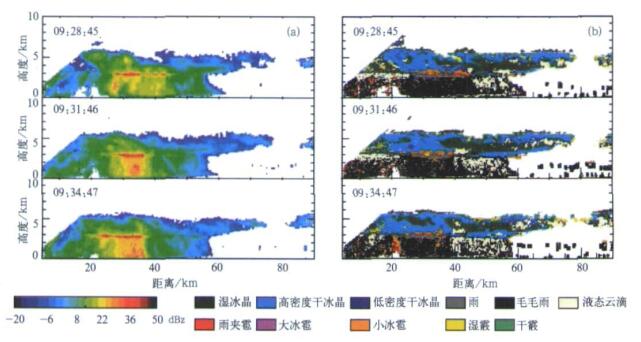
| 图 4. 成熟阶段的雷达反射率因子 (a) 和相态分类结果 (b) Fig 4. CAMRa Zhh(a) and classification results (b) during mature phase | |
|
|
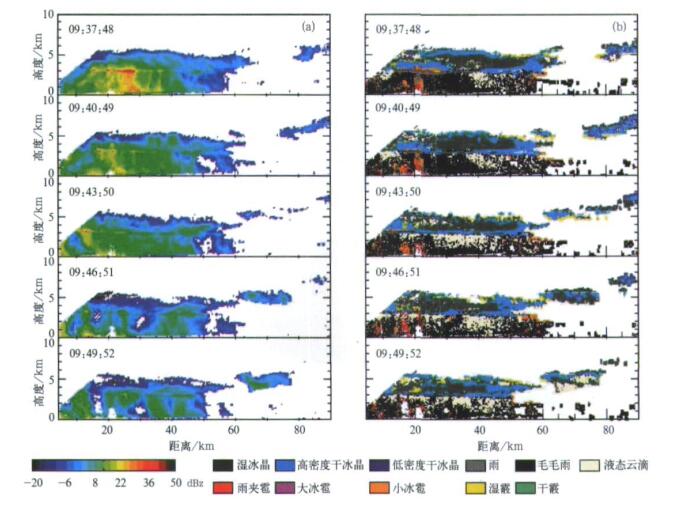
| 图 5. 消散阶段的雷达反射率因子 (a) 和相态分类结果 (b) Fig 5. CAMRa Zhh(a) and classification results (b) during dissipating phase | |
初始阶段:开始存在明显的两部分云体, 对于左侧云体, 通过此前的雷达回波 (图略) 可知为前一降水过程逐步减弱后的降水层状云, 内部有较为明显的零度层亮带出现, 其高度在3~4 km之间, 从相态反演结果可以看出零度层亮带以上云体粒子相态主要为冰相, 上部主要为湿冰晶, 之下为层状分布的高密度干冰晶, 零度层亮带为冰相与液相的过渡区域, 在此区域中雷达回波的大值区 (45 km左右) 有小冰雹存在, 零度层亮带以下主要为液相的毛毛雨滴和大雨滴组成, 而距离20 km处附近出现的大冰雹通过差分反射率图 (图略) 可知为污染所致。对于右侧的非降水高层云, 其云体大部在4 km高度以上, 最上部为冻结程度较高的高密度干冰晶, 其下依次为湿冰晶、液态云滴, 呈层状分布; 4 km以下区域, 为散落的液态粒子, 冰晶融化、散落、碰撞过程是其形成的主要原因, 但由于蒸发作用而没有降落到地面, 其存在并进一步发展是降水形成的信号。随后, 左侧云体中对流云开始发展, 内部逐步出现两个明显的回波大值区, 发展较旺盛时, 大值区相态几乎全部为液态, 并且其上的冰晶也融化成液态, 然而随着右侧层状云的逐步发展并与之相接, 左侧云体没能得到进一步发展, 大值区迅速减弱, 但4 km以上区域继续保持液态, 右侧云体中心大值区逐步形成, 分层的相态结构逐步减弱, 中心区域处的液态粒子逐步演变成冰相与液相共存的混合体, 而其上出现较大范围的液态小粒子。随着两部分云体的进一步合并, 大值区也合并成一个强度更强的区域, 而其上的液态粒子逐步转化为冰相, 而中心大值区域逐步发展成大的冰相与液态粒子, 逐步形成降水。
成熟阶段:云体相态较为稳定, 范围较大的大值区以上冰相粒子进一步冻结, 湿冰晶逐步转变为高密度干冰晶, 中部3 km高度附近是大的冰相粒子与大的液态粒子共存的过渡区域, 其下形成降水。消散阶段:云体上部干冰晶范围逐步减小, 湿冰晶范围逐步扩大, 呈现高密度干冰晶包裹湿冰晶的情况, 高度中部区域尺度较大的冰相和液相粒子消失, 零度层亮带逐步消失, 其下粒子相态为液态云滴或大的雨滴。
综上可见, 在此次层状云降水过程中, 初始阶段层状云相态呈现分层结构, 从上至下依次为高密度干冰晶、湿冰晶和液态云滴。随着进一步发展, 云体中心出现回波大值区, 分层结构逐步被打破, 初始阶段大值区中回波最强的区域为大的冰相粒子, 其他区域均为液态, 随后回波大值区上部粒子开始向冰相转化, 这一过程大约经历18 min, 到成熟阶段, 这部分粒子进一步冻结为高密度干冰晶, 持续大约10 min, 随后降水逐步减弱, 零度层亮带逐步消失, 零度层以上云粒子相态呈现高密度干冰晶包裹湿冰晶的情况。
5 小结本文建立了基于双偏振雷达RHI探测量与温度廓线数据的云粒子相态反演模糊逻辑算法, 所使用的探测量包括反射率因子、线性退偏比和差分反射率, 针对发展较为稳定的降水层状云对水凝物粒子相态进行分类反演, 反演出的相态包括毛毛雨、雨、低密度干冰晶、高密度干冰晶、湿冰晶、干霰、湿霰、小冰雹、大冰雹、雨夹雪和液态云滴等11种, 并使用连续观测的雷达数据对一次较为完整的层状云降水过程进行了分析, 将降水过程分为初始、成熟、消散3个阶段, 对每个阶段中水凝物相态进行反演, 对其变化情况进行分析, 得到如下结论:
1) 双偏振雷达的连续探测可用来分析降水过程中水凝物粒子的演变情况。
2) 初始阶段层状云相态呈现分层结构, 从上至5期程周杰等:双偏振雷达对一次水凝物相态演变过程的分析599下依次为高密度干冰晶、湿冰晶和液态云滴; 初始阶段云体中的回波大值区核心区域为大的冰相粒子, 其余部分为液态粒子。
3) 在初始到成熟的阶段演变中, 回波大值区上部液态粒子逐步向冰相转化。
4) 消散阶段云中零度层亮带逐步消失, 温度零度层以上云粒子结构呈现高密度干冰晶包裹湿冰晶的情况。
本文提供了一种研究云微物理结构的思路, 但也存在一些问题值得进一步讨论, 例如, Beta型成员函数轴对称结构的合理性、反演结果中毛毛雨面积过大等, 同时结果验证工作也有待开展。
致谢 感谢英国卢瑟福阿普尔顿 (Rutherford Appleton) 实验室提供了本文所需的CAMRa双偏振雷达数据。| [1] | Seliga T A, Bringivn V N, Potential use of radar differential reflectivity measurements at orthogonal polarizations for measuring precipitation. J Appl Meteor, 1976, 15: 69–76. DOI:10.1175/1520-0450(1976)015<0069:PUORDR>2.0.CO;2 |
| [2] | 刘黎平, 张鸿发, 王致君, 等. 利用双线偏振雷达识别冰雹方法初探. 高原气象, 1993, 12, (3): 333–337. |
| [3] | Aydin K, Seliga T A, Balaji V, Remote sensing of hail with a dual linear polarization radar. J Climate Appl Meteor, 1986, 25: 1475–1484. DOI:10.1175/1520-0450(1986)025<1475:RSOHWA>2.0.CO;2 |
| [4] | Bringi V N, Seliga T A, Aydin K, Hail detection with a differential reflectivity radar. Science, 1984, 225: 1145–1147. DOI:10.1126/science.225.4667.1145 |
| [5] | Hall P M, Goddard J W F, Cherry S M, Identification of hydrometeors and other targets by dual-polarization radar. Radio Sci, 1984, 19: 132–140. DOI:10.1029/RS019i001p00132 |
| [6] | Bringi V N, Vivekanandan J, Tuttle J D, Multiparameter radar measurements in Colorado convective storms.Part Ⅱ:Hail detections tudies. J At mos Sci, 1986, 43: 2564–2577. |
| [7] | 刘黎平, 钱永甫, 王致君. 用双线偏振雷达研究云内降水粒子相态及尺度的空间分布. 气象学报, 1996, 54, (5): 590–598. |
| [8] | 漆梁波, 肖辉, 黄美元, 等. 双线偏振雷达识别冰雹的数值研究. 大气科学, 2002, 26, (2): 230–240. |
| [9] | 刘黎平. 双线偏振多普勒天气雷达估测混合区降雨和降雹方法的理论研究. 大气科学, 2002, 26, (6): 761–772. |
| [10] | Straka J M, Zrnic D S, An Algorithm to Deduce Hydrometeor Types and Contents from Multi-parameter Radar Data. Preprints, 26th Conf on Radar Meteorology, 1993: 513–515. |
| [11] | Zrnic D S, Ryzhkov A V, Polarimetry for weather surveillance radar. Bull Amer Meteor Soc, 1999, 80: 389–406. DOI:10.1175/1520-0477(1999)080<0389:PFWSR>2.0.CO;2 |
| [12] | Vivekanandan J, Zrnic D S, Ellis S M, et al. Cloud microphysics retrieval using S-band dual-polarization radar measurements. Bull Amer Meteor Soc, 1999, 80: 381–388. DOI:10.1175/1520-0477(1999)080<0381:CMRUSB>2.0.CO;2 |
| [13] | Liu H, Chandrasekar V, Classification of hydrometeor type based on polarimetric radar measurements:Development of fuzzy logic and neuro-fuzzy systems, and in situ verification. J Atmos Ocean Technol, 2000, 17: 140–164. DOI:10.1175/1520-0426(2000)017<0140:COHBOP>2.0.CO;2 |
| [14] | Straka J M, Zrnic D S, Bulk hydrometeor classification and quantification using polarimetric radar data:Synthesis of relations. J Appl Meteor, 2000, 39: 1341–1372. DOI:10.1175/1520-0450(2000)039<1341:BHCAQU>2.0.CO;2 |
| [15] | Zrnic D S, Ryzhkov A, Straka J, et al. Testing a procedure for automatic classification of hydrometeor types. J Atmos Ocean Technol, 2001, 18: 892–913. DOI:10.1175/1520-0426(2001)018<0892:TAPFAC>2.0.CO;2 |
| [16] | Aydin K, Singh J, Cloud ice crystal classification using a 95 GHz polarimetric radar. J Atmos Oceanic Technol, 2004, 21: 1679–1688. DOI:10.1175/JTECH1671.1 |
| [17] | 曹俊武, 刘黎平, 葛润生. 模糊逻辑法在双线偏振雷达识别降水粒子相态中的研究. 大气科学, 2005, 29, (5): 827–836. |
| [18] | 曹俊武, 刘黎平, 陈晓辉, 等. 3836C波段双线偏振多普勒雷达及其在一次降水过程中的应用研究. 应用气象学报, 2006, 17, (2): 192–200. |
 2009, 20 (5): 594-601
2009, 20 (5): 594-601