2. 中国科学院研究生院, 北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049
利用闪电定位系统可以实时获得闪电发生的时空分布、强度和极性等特征, 这些参量不仅对雷电监测和防御非常重要, 对灾害性天气的监测和预警也具有重要作用[1]。到达时间 (time-of-arrival, TOA) 闪电定位系统的研究工作始于Proctor[2]的五站定位系统。由于其具有较高的探测性能和定位精度, 在闪电定位系统中广泛应用。LPATS (Lightning Position and Tracking System)[3]、LMA (Lightning Mapping Array)[4]等闪电探测系统都采用了TOA定位方法, 美国国家闪电监测网 (National Lightning Detection Network, NLDN)[5]则采用TOA和磁定向 (DF) 联合定位方法。TOA定位方法也是我国闪电监测网广泛使用的主要方法之一。
闪电定位系统中, 如何采用科学的定位算法有效减小定位误差是人们普遍关注的问题。定位算法是闪电定位系统的核心技术之一, 它关系到能否充分利用闪电监测网获得的基本数据进行有效定位, 因而直接影响闪电数据的质量和应用。早在20世纪60年代, 国外已经开展闪电定位算法的研究工作。Lewis等[6]、Oetzel等[7]利用地面无线电频率测量闪电到达时间, 进行了定位和误差分析比较。Holle等[8]利用改进的双曲线方程来确定球面闪电辐射源的二维位置, 该方法已应用于LPA TS闪电定位系统中。Koshak等[9]提出适用于TOA闪电定位系统的“超平面模型”, 并发现站网几何分布、测站数目、辐射源位置、计时误差和天线定位误差是影响定位精度的主要因素。我国在闪电定位算法方面也开展了大量研究工作。蒋正龙[10]详细分析了湖南省雷电定位系统的定位原理和方法。赵文光等[11]建立了基于球面坐标的闪电综合定位模型。在多站探测情况下, 该模型能够利用时间和方位信息对闪电进行综合定位。
定位误差是表征闪电定位系统性能的重要参数和系统指标。研究表明:系统的定位精度与定位模型、闪电判据、场地延时误差、GPS时钟误差、测站距离、地形地貌等复杂因素有关[12]。国外有关闪电定位误差的研究主要分为两类。一类研究针对定位中的随机误差, 利用最小二乘法对闪电位置进行优化处理。另一类研究集中在如何确定场地误差。Mach等[12]首先发展了利用闪电方位信息计算场地误差的方法, 并利用全方位照相记录与DF资料进行对比来确定系统的定位误差。Schutte等[13]利用无线电交互发射和接收性质不变原理, 分析了实测DF场地误差对定位结果的影响。Ronald等[4]建立了闪电定位系统距离误差几何模型Δr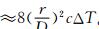
闪电定位系统的误差分析研究在闪电监测网的实际应用中具有重要作用。一方面, 定位误差能够对监测网的定位效果进行描述, 帮助数据使用者掌握定位数据的精度和质量[19]。另一方面, 不同测站分布的误差分析能够为站址的合理选择提供依据。测站数目和布站方式对闪电定位系统的探测精度有很大影响, 合理的站点布局不仅可以提高定位精度, 还可以充分利用站点资源, 以尽量少的测站达到尽量高的定位精度[20]。基于以上目的, 本文侧重于时间差定位系统的误差分析, 在时间差闪电定位算法的基础上, 利用蒙特卡罗计算机模拟方法, 对闪电定位误差进行定量评估, 并详细分析探测子站数目、布站方式和站址基线长度对定位结果的影响。研究结果能够为闪电监测网的站址选择、子站布设等实际工作提供重要参考依据。
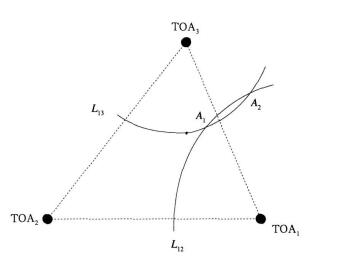
1 TOA闪电定位原理到达时间法是通过测量闪电产生的电磁脉冲信号到达不同测站的时间差来进行闪电定位的技术方法[21]。两个以上放置于不同位置的探测子站探测闪电电磁脉冲到达本站的绝对时间, 每两个测站之间的时间差构成一条双曲线, 两条双曲线的交点就是闪电的发生位置。图 1中TOA 1, TOA2, TOA 3为3个时间差探测子站, 设闪电信号到达各站的时间分别为t1, t2, t3, 可得出探测子站的时间差分别为Δt12, Δt13, Δt23。TOA 1与TOA 2确定的双曲线为L12, TOA 1与TOA 3确定的双曲线为L13, L 12与L13的交点A1即为闪电发生的真实位置, 另一个交点A2称为“伪点”[8], 可以通过辅助条件加以排除。当测站数目大于3时, 多于3条的双曲线不可能交于一点, 此时需要采用优化算法计算闪电最可能发生的位置[22]。
|
|
| 图 1. TOA定位原理示意图 Fig 1. Sketch map of TOA locating technique | |
TOA闪电定位系统一般包括4个或4个以上的探测子站, 以确保定位结果的唯一性。WMO《气象仪器和观测方法指南》建议, TOA区域闪电定位系统的站点数目以4~6站为宜[23]。由于TOA定位系统中几乎不存在场地误差, 利用GPS技术把各测站的时间同步到纳秒级, 当时间误差≤1 μs时, 最大定位误差≤1 km, 因此具有相对较高的定位精度。
2 基于TOA的闪电定位算法 2.1 定位算法TOA闪电定位算法能够利用子站的到达时间信息, 确定闪电的位置和发生时间。在地闪定位系统的算法设计中, 未考虑闪电高度的影响, 并且忽略了大气折射, 认为从闪电源到探测站的传输路径为直线。计算中用到的地球半径R=6378.137 km, 光速C=3×108 m · s -1。假设 (x, y, t) 是闪电的真实位置和发生时间, (xi, yi, ti) 是第i个探测子站的位置和到达时间。假定有N (N≥4) 个测站同时接收到该闪电信号, 则对第i站有:
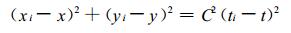
|
(1) |
对j站有:
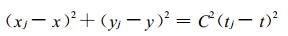
|
(2) |
将式 (1) 和 (2) 的展开式相减得
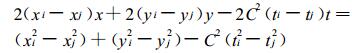
|
(3) |
对于包含N个探测子站的闪电定位系统, 两两测站之间的组合有C2N种, 因此能够建立C2N个类似于式 (3) 的方程。当进行组合的两个测站到达时间差Δt≤1 μs时, 由这两个测站组成的方程不参与计算。
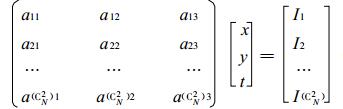
|
(4) |
其中, a i1=2(xi-x j), a i2=2(y i-y j), ai3=-2C2(ti-tj), I i=(x2 i-x2j)+(y2 i-y 2 j)-2C (t2 i-t2j) (i, j=1, 2, …, C2 N)
将方程写成矩阵形式
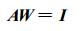
|
(5) |
式 (5) 中, A, W, I分别为系数矩阵、变量矩阵和常数列矩阵。当系数矩阵A为非奇异可逆矩阵时[24], 该矩阵方程的解为
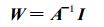
|
(6) |
对于一个N≥4的多站定位系统, 进行闪电定位前应进行闪电事件的同步检验, 以确定哪些测站接收到的信号来自于同一个闪电。闪电事件同步检验主要包括时间差检验和闪电特征检验两个方面。
2.2.1 时间差检验根据双曲线定义, 若探测子站A, B的时间差Δt AB满足以下条件, 则认为两站接收到的信号可能来自同一闪电:
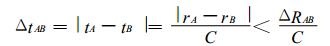
|
(7) |
式 (7) 中, tA, tB分别表示闪电到达A站和B站的时间, r A, rB表示闪电与A, B站的距离, ΔRAB表示A, B两站之间的距离。若满足此判据, 则认为A, B两站接收到的脉冲信号可能来自同一闪电, 可参与多站定位计算。
2.2.2 闪电特征检验满足时间差条件的脉冲信号如果具有不同的闪电特征, 也不能认为是同一个闪电信号。例如, 两个探测站接收到的闪电信号满足时间差条件, 但一个是正地闪, 一个是负地闪, 则不能将二者归为同一个闪电。因此, 除满足时间差条件外, 闪电同步判据中还应包括对闪电特征的检验。闪电特征检验应至少包括闪电类别 (云闪、地闪) 检验和电流极性 (正、负) 检验, 将闪电特征与时间差统一考虑, 以增加闪电事件同步检验的严格性。
3 定位误差分析利用时差法进行闪电定位时, 误差来源主要有两种:一种是闪电定位仪的测量误差, 这主要取决于GPS的测时精度; 另一种是探测子站的数目和布站方式[4]。本研究在观测条件一定的情况下, 分析了测站数目、布站方式和基线长度对定位结果的影响。
闪电定位系统中探测子站的记录时间为真实闪电传播时间和测时误差之和。根据子站记录时间进行双曲线交汇得到的闪电位置与实际位置存在一定偏差, 这个偏差就是该点的定位误差。为了对闪电定位误差进行定量评估, 采用蒙特卡罗计算机模拟方法, 选择研究区域经纬度范围为7°×7°, 中心经纬度为39.0°N, 116.0°E。在研究区域内任意给定一个闪电位置, 其到各个测站的准确时间可知, 然后增加均值为0、均方差为1 μs (u=0, ζ=1 μs) 的正态分布随机误差, 由计算值得到一个新的闪电位置, 则计算的闪电位置和给定的闪电位置之差就是该点的定位误差。在模拟过程中, 假设闪电定位系统中的所有探测子站均参与定位计算[14, 25-26], 并将研究区域等分成19881(即141×141) 个网格, 网格大小为0.05°×0.05°。每个网格中模拟发生1000个闪电, 因此共模拟了19881000(即19881×1000) 个闪电, 1000个闪电定位误差的平均值认为是该网格点的定位误差。通过计算每个网格点的误差, 得到整个区域的误差分布。定位误差计算主要包括以下步骤:①计算闪电从网格中心到每个测站的到达时间; ②在到达时间上增加随机时间误差, 模拟闪电的真实传输情况; ③利用TOA定位算法对闪电进行定位; ④计算定位结果与真实值之差, 即闪电的定位误差; ⑤每个网格模拟发生1000个闪电, 其定位误差的平均值作为该网格点的定位误差。
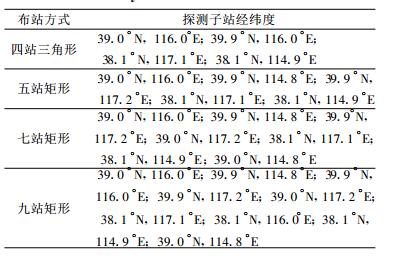
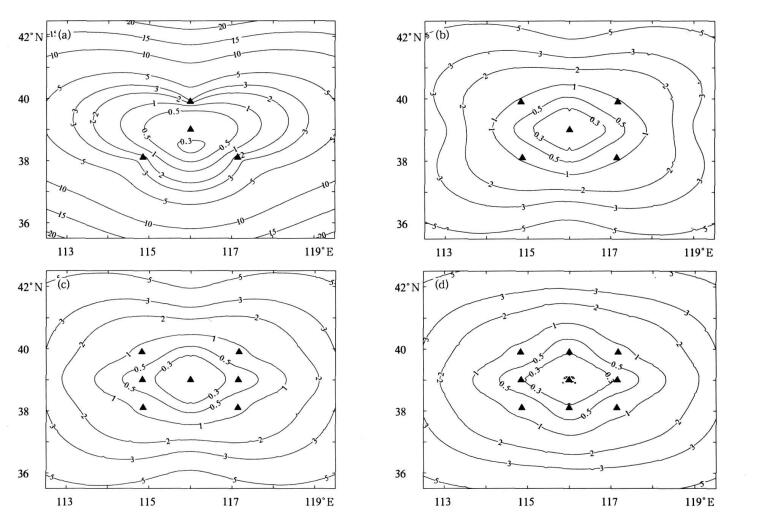
4 结果分析 4.1 测站数目对定位结果的影响在闪电定位系统中, 探测子站的数目是系统定位精度的主要影响因素之一。为了分析测站数目对定位结果的影响, 选择环绕中心站的准对称布站方式, 对四站、五站、七站和九站4种相似结构的布站方式进行比较。为了排除站网覆盖区域不同而产生的定位结果差异, 规定探测子站在经度和纬度上的最大站距均为200 km, 准对称布站方式下探测子站的经纬度坐标见表 1。图 2给出了4种布站方式下, 不同测站数目定位系统的误差等值线图。从图 2可以看出, 在准对称布站方式下, 九站定位系统的误差最小, 研究区域内最大定位误差为5 km, 五站和七站系统的定位结果其次。四站三角形系统的定位误差最大, 研究区域内出现了20 km的高误差。从图 2中可以看出, 定位误差与闪电到站网中心的距离有密切关系。闪电距离探测网络中心越远, 其定位误差越大。此外, 在布站方式相同的条件下, 测站数目越多, 定位误差小于1 km的区域面积越大。
|
|
表 1 准对称布站方式下探测子站经纬度坐标 Table 1 Longitude and latitude of stations in symmetrical network |
|
|
| 图 2. 准对称布站方式下不同测站数目的误差等值线 (单位:km; 三角形表示探测子站) (a) 四站三角形网络, (b) 五站矩形网络, (c) 七站矩形网络, (d) 九站矩形网络 Fig 2. Contour map of locating error versus different station number in symmetrical networks (unit:km; triangle denotes locating station)(a) triangle network with four stations, (b) rectangle network with five stations, (c) rectangle network with seven stations, (d) rectangle network with nine sta tions | |
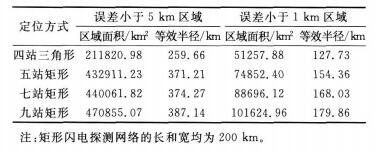
为了定量分析误差的大小, 引入两个物理量:①误差小于5 km和1 km区域的面积 (单位:km2); ②误差小于5 km和1 km区域的等效半径 (单位: km)。表 2给出了准对称布站方式下, 不同测站数目定位系统中两个物理量的计算结果。可以看出, 四站三角形系统等效半径最小, 分别为259.66 km和127.73 km; 五站矩形和七站矩形系统的等效半径依次增大; 九站矩形系统的等效半径最大, 分别为387.14 km和179.86 km。四站三角形、五站矩形、七站矩形、九站矩形的误差小于5 km和1 km区域的面积和等效半径依次增大, 定位误差依次减小。从4种定位结果的比较中可以看出, 在相同的准对称布站方式下, 随着测站数目的增多, 误差小于5 km和1 km的区域面积逐渐增大, 等效半径也逐渐增大, 定位误差逐渐减小。
|
|
表 2 准对称布站方式下测站数目的定位结果物理量比较 Table 2 Locating error of different station number with symmetrical network |
4.2 布站方式对定位结果的影响
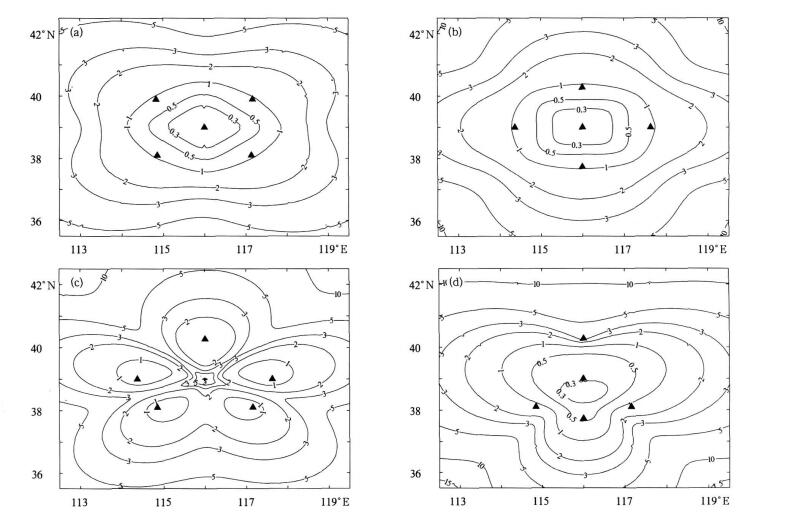
在闪电定位系统中, 不同的站点布设方式可以达到不同的定位效果。合理的站点布局不仅可以充分利用站点资源, 而且对提高定位精度、扩大探测区域具有十分重要的作用。在观测条件确定的前提下, 如何使辐射源在受控区域内具有较高的定位精度, 关键是选择最优的站址布局方案。以五站定位系统为例, 分析了矩形、菱形、星形、三角形4种布站方式对定位结果的影响。为了消除站距不同而造成的定位结果差异, 规定所有子站到达探测网络中心的距离均为100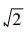
|
|
| 图 3. 五站定位系统中不同布站方式的定位误差等值线 (单位:km; 三角形表示探测子站) (a) 矩形网络, (b) 菱形网络, (c) 星形网络, (d) 三角形网络 Fig 3. Contour map of locating error versus different network geometry with five stations (unit:km; triangle denotes locating station)(a) rectangle network, (b) diamond network, (c) star network, (d) triangle network | |
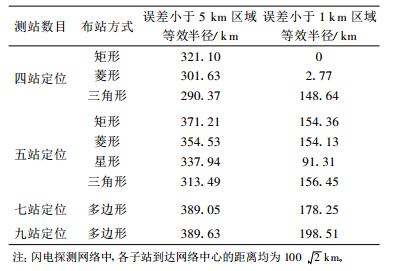
表 3给出了四站、五站、七站和九站定位系统中不同布站方式下的定位结果。所有探测子站到达网络中心的距离均为100 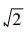
|
|
表 3 不同测站数目、不同布站方式下的定位结果物理量比较 Table 3 Comparison of locating errors with different stations number and network geometry |
4.3 基线长度对定位结果的影响
TOA闪电定位系统根据其基线长度可分为3种基本类型:①超短基线系统 (几十到几百米); ②短基线系统 (几十公里); ③长基线系统 (几百到几千公里)[22]。超短基线系统设备简单且不存在多站同步问题, 但由于定位精度较差、有效探测距离短而未被广泛使用。目前, TOA闪电定位系统大多采用短基线和长基线多站观测, 基线长度为几十到几百公里, 可以对脉冲类波形进行很好的定位。随着GPS系统的广泛应用, TOA闪电辐射源定位系统的定位精度将得到较大提高。
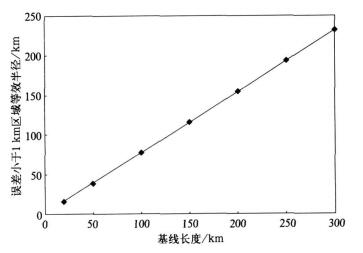
为了检验基线长度对定位结果的影响, 以五站定位系统为例, 采取正方形加中心站的布站方式, 随机时间误差设为1 μs, 分析基线长度 (正方形边长) 分别为20, 50, 100, 150, 200, 250, 300 km 7种情况下的定位误差。从图 4可以看出, 在测站数目、布站方式和随机时间误差不变的情况下, 误差小于1 km区域等效半径随基线长度的增加而增大, 二者呈线性正相关。在仪器有效探测范围内, 基线长度越长, 探测子站之间的距离越大, 探测网所覆盖的区域越大。由于网络覆盖区域内的定位精度较高, 因此整个研究范围内定位误差小于1 km的区域面积增大。以上给出的只是理想情况下的理论分析结果, 在实际站网确定基线长度时, 应对仪器的探测性能、GPS测时精度、地形地貌、探测网的具体用途等多种因素进行综合考虑。
|
|
| 图 4. 误差小于1 km等效半径随基线长度的变化 Fig 4. Radius of area where locating error is less than 1 km versus baseline of the network | |
5 讨论
在四站定位系统中发现, 矩形站网布局的定位结果存在一个高误差区域, 这个区域位于矩形两条相互垂直的对称轴上 (图 5)。这是由于当站网呈矩形分布时, 定位系统的4个探测子站相对于中心点呈对称分布, 两条对称轴上的点到两侧子站的距离相等, 因此理论传播时间相同。此时的到达时间差主要取决于随机时间误差, 因而很小的扰动就会给定位结果带来很大误差。Koshak等[9]在闪电线性定位算法研究时曾发现同样问题并指出, 当闪电位于或非常接近于四站矩形的两条对称轴时, 定位误差将快速增大。这是由于当闪电位于上述区域时, 矩阵方程AW=I中的A变为奇异矩阵, A的最小特征值接近于0, A -1变得非常大, 因此造成很大的定位误差。Koshak等称矩形对称轴及其附近区域为四站矩形探测网络的盲区, 闪电距离对称轴越近, 其定位误差就越大。对于任何一个定位网络, 如果探测子站在某个方向上成线性排列, 那么就会出现类似问题, 从而在测站排列方向上不能对闪电进行准确定位[4]。按照Ronald等[4]的布局原则:一个好的闪电定位站网, 必须保证对于任一雷电波形, 在其传输方向的垂直方向上都至少有3个间距足够大的测站 (文献[4]中图 11)。按照这种布局原则, 在4.2节的四站矩形站网中心增加1个测站形成五站系统, 结果显示定位误差明显减小, 高误差区域消除。因此, 在实际站网布设工作中应当尽量避免四站矩形这种对称布站方式, 通过在矩形中心增加一个探测子站的方法来减小误差。

|
|
| 图 5. 四站矩形定位系统的高误差区域 (单位:km) Fig 5. High locating errors in a rectangle network with four stations (unit:km) | |
6 结论
利用蒙特卡罗模拟方法, 实现了对TOA闪电定位误差的计算机模拟, 探讨了测站数目、布站方式和站址基线长度对定位结果的影响, 主要得出以下结论:
1) 闪电定位系统中, 定位误差不是简单地随测站数目的增多而减小, 定位误差与子站的布设方式紧密相关。就矩形、菱形、星形和三角形4种几何布局来看, 矩形加中心站布局具有相对较高的定位精度。
2) 闪电定位系统中, 探测网络覆盖区域外的定位误差大于区域内的定位误差, 且误差随着与网络中心距离的增加而增大。当定位系统的子站布设方式一定时, 子站数目越多, 定位误差越小。
3) 区域闪电定位系统应至少包含4个探测子站。一个好的闪电定位站网, 必须保证对于任一雷电波形, 在其传输方向的垂直方向上都至少有3个间距足够大的测站。四站矩形站网存在的定位盲区, 可通过在中心位置加布1个站来消除。
4) 在仪器允许的探测范围内, 站址基线越长, 站网覆盖区域越大, 定位误差越小。在实际站网布设中, 应当综合考虑仪器探测性能、GPS测时精度、地形地貌、站网用途等多种因素来确定站址基线长度。
我国多个地区采用时间差和磁定向联合定位方法的闪电定位系统, 对于该系统的定位误差理论分析和试验检验, 以及定位算法的优化设计仍然需要进一步研究。
致谢 感谢中国科学技术大学陶善昌教授在文章修改过程中提出的宝贵意见和建议。| [1] | 张义军, 周秀骥. 雷电研究的回顾和进展. 应用气象学报, 2006, 17, (6): 829–834. |
| [2] | Proctor D E, A hyperbolic system for obtaining VHF radio pictures of lightning. J Geophys Res, 1971, 76: 1478–1489. DOI:10.1029/JC076i006p01478 |
| [3] | Kenneth L Cummins, Philip Krider E, Malone D, The US National Lightning Detection Network and application of cloud-toground lightning data by electric power utilities. IEEE Transactions on Electromagnetic Compatibility, 1998, 40, (4): 465–479. DOI:10.1109/15.736207 |
| [4] | Ronald J Thomas, Paul R Krehbiel, William Rison, et al. Accuracy of the Lightning Mapping Array. J Geophys Res, 2004, 109. |
| [5] | Orville E Richard, Development of the National Lightning Detection Network. American Meteorological Society, 2008, 2: 180–190. |
| [6] | Lewis E A, Harvey R B, Rasmussen J E, Hyperbolic direction fin ding with sferics of transatlantic origin. J Geophys Res, 1960, 65: 1879–1905. DOI:10.1029/JZ065i007p01879 |
| [7] | Oetzel G N, Pierce E T, VHF technique for locating lightning. Radio Sci, 1969, 4: 199–201. DOI:10.1029/RS004i003p00199 |
| [8] | Holle R L, Lopez R E, Overview of Real-time Lightning Detection Systems and Their Meteorological Uses. NOAA Tech Mem, ERLNSS L-102, 1993. |
| [9] | Koshak J William, Solakiewicz J Richard, On the retrieval of lightning radio sources from time-of-arrival data. J Geophys Res, 1996, 101, (D21): 26631–26639. DOI:10.1029/96JD01618 |
| [10] | 蒋正龙. 湖南雷电定位系统定位算法的研究. 湖南电力, 2000, 20, (6): 6–9. |
| [11] | 赵文光, 陈家宏, 张勤, 等. 新的雷电综合定位系统的定位计算. 高电压技术, 1999, 25, (4): 66–68. |
| [12] | Mach M Douglas, Donald R MacGorman, David Rust W, et al. Site errors and detection efficiency in a magnetic direction finder network for locating lightning strikes to ground. J Atmos Ocean Technol, 1986, 3: 67–74. DOI:10.1175/1520-0426(1986)003<0067:SEADEI>2.0.CO;2 |
| [13] | Schutte T, Pissler E, Israelsson S, A new method for the measurement of the site errors of a lightning direction finder:Description and first results. J Atmos Ocean Technol, 1987, 4: 305–311. DOI:10.1175/1520-0426(1987)004<0305:ANMFTM>2.0.CO;2 |
| [14] | Koshak J William, Solakiewicz R J, Blakeslee R J, et al. North Alabama Lightning Mapping Array (LMA):VHF source retrieval algorithm and error analyses. J Atmos Ocean Technol, 2004, 21: 543–558. DOI:10.1175/1520-0426(2004)021<0543:NALMAL>2.0.CO;2 |
| [15] | 陈明理, 刘欣生, 郭昌明, 等. 确定雷电定位系统场地误差的参数化方法. 高原气象, 1990, 9, (3): 307–319. |
| [16] | 杨波, 邱实, 宁军, 等. 闪电定位误差及探测效率评估. 解放军理工大学学报, 2006, 7, (5): 506–510. |
| [17] | 张勤, 王光财, 吴维宁, 等. 新的综合雷电定位系统的误差计算. 高电压技术, 2000, 26, (2): 54–56. |
| [18] | 赵文光, 张瑞芳, 吴维宁. 雷电探测网的精度估计. 华中科技大学学报, 2002, 19, (1): 58–60. |
| [19] | Kenneth L Cummins, Martin J Murphy, Edward A Bardo, et al. A combined TOA/ MDF technology upgrade of the US National Lightning Detection Network. J Geophys Res, 1998, 103, (D8): 9035–9044. DOI:10.1029/98JD00153 |
| [20] | Schutte T, Pissler E, Filipovic D, et al. Acceptance of lightning detectors and localization systems under different damping conditions. J Atmos Ocean Technol, 1987, 4: 401–410. DOI:10.1175/1520-0426(1987)004<0401:AOLDAL>2.0.CO;2 |
| [21] | 孟青, 赵均壮, 张义军, 等. 闪电监测定位系统 (第1部分):技术条件. 中华人民共和国气象行业标准, QX/ T79-2007, 2007. |
| [22] | Vladimir A Rakov, Martin A Uman, Lightning Physics and Effects. Cambridge: Cambridge University Press, 2003: 555-587. |
| [23] | World Meteorological Organization.Guide to Meteorological Instruments and Methods of Observation (6th Edition). 1996:359-360. |
| [24] | Koshak W J, Solakiewicz R J, On the retrieval of lightning radio sources from the time-of-arrival data. J Geophys Res, 1996, 101: 26631–26639. DOI:10.1029/96JD01618 |
| [25] | Shao Xuanmin, Mark Stanley, Amy Regan, et al. Total lightning observation with the new and improved Los Alamos Sferic Array (LASA). J Atmos Ocean Technol, 2006, 23: 1273–1288. DOI:10.1175/JTECH1908.1 |
| [26] | Hager W William, Wang Dongxiong, An analysis of errors in the location, current and velocity of lightning. J Geophys Res, 1995, 100, (D12): 25721–25729. DOI:10.1029/95JD02527 |
 2009, 20 (4): 402-410
2009, 20 (4): 402-410