2. 南京信息工程大学江苏省气象灾害重点实验室, 南京 210044
2. Jiangsu Key Laboratory of Meteorological Disaster, NUIST, Nanjing 210044
沙瓦特指数是20世纪50年代引入的一个稳定度指数[1], 定义为500 hPa等压面上环境温度与850 hPa等压面上的湿空气块干绝热抬升, 到达抬升凝结高度后湿绝热上升至500 hPa时气块温度的差值。它反映了大气稳定度状况, 当沙瓦特指数小于0时, 表示层结不稳定, 且负值越大, 不稳定程度越大, 反之则是稳定的。该指数的提出在雷暴指数发展进程中具有里程碑意义, 它是判断对流性天气的指标[1-3], 也是其改进指数[4-5]、瑞士指数[6]及抬升指数[7-11]的基础。其算法核心部分是计算500 hPa的气块温度。计算气块温度的传统方法是图表法[12-13], 如Gary等[12]在计算抬升凝结高度处的要素后, 通过查表插值的方法计算500 hPa气块温度。目前, 为了适应资料批量处理和预报时效性的要求, 多采用某种算法直接计算沙瓦特指数。但是, 不同计算方案的计算精度存在较大差异[14], 可比性差, 从而束缚了这一重要天气指标的通用性。而通用性的前提是确保气象指标的计算精度, 改进沙瓦特指数算法就是为了提高其计算精度。
实际上, 由于大气演变的复杂性, 往往引入包含多种效应的诊断量来判别大气状态。一些诊断量是其他诊断量的多级复合函数, 在其计算过程中需要考虑误差传递、放大效应, 这就要求中间诊断量的计算应达到较高精度。因此, 提高计算精度的需求具有普遍性。在沙瓦特指数的计算方案中引入二分法可作为改进其他诊断量算法的参考。
1 二分法简介二分法的数学问题可描述为:当函数y=f(x) 在区间[a, b]上是单调函数, 已知y且y ∈ [min (f(a), f(b)), max (f(a), f(b))], 采用对x的定义区间折半搜索的方法求取对应自变量x的数值, 使得y=f(x)。二分法的具体步骤是:
①先设定初始的迭代边界值xLn=a, xRn=b, 迭代次数n=0。
②设定xtn+1=0.5(xLn+ xRn), 计算ytn+1=f(xtn+1)。
③通过比较ytn+1和y的关系及函数单调性质来确定下一次迭代边界, 确保y在新的折半后的区间中。当f(x) 为增函数时, 如果ytn+1 > y, 则xLn+1=xLn, xRn+1=xtn+1; 如果ytn+1 < y, 则xLn+1=xtn+1, xRn+1=xRn。
④第 (n+1) 次迭代, 重复②和③步骤, 直至求解的精度满足xRn-xLn≤ε, 这时x=xtn就是所要求的解。其中上标表示迭代次数, 下标R, L, t以及max和min分别表示右边界、左边界、试解变量以及极大值和极小值。
上述分析表明, 二分法每次迭代后试解区间变为原来的二分之一, 进行n次迭代后, 区间宽度变为原来的1/2n, 即从理论上讲二分法可达到求解的任意指定精度。二分法的计算次数是有限的, 假设初始迭代区间的宽度为1000, 迭代精度取为0.01, 根据迭代区间呈指数变化的特性, 可得计算步骤约为17步。上述可表示大多数需要迭代求解的大气诊断量计算。当然, 对气象要素的计算也可采用等距试解方式, 如对抬升凝结高度上要素的计算[15]。但是, 等距试解的每一步计算实质上仅是搜索真值的位置, 对试解精度没有贡献; 而二分法不但搜索真值的位置, 还提高了试解精度, 每次提高一倍。若精度在小数点后提高一位, 等距试解法的计算量需要增至原来的10倍, 而二分法仅增加3~4次计算 (精度为原来的1/8~1/16) 即可。由此看来, 二分法具有精度高、收敛速度快的优点。
2 计算沙瓦特指数的步骤 2.1 计算850 hPa比湿用t1, td1, t2表示下层等压面的温度、露点温度和上层等压面的温度 (单位:℃); p1和p2表示下层和上层等压面的气压 (单位:hPa, 通常为850 hPa和500 hPa)。下文无特殊说明时, 下标1表示下层, 下标2表示上层。将露点温度代入式 (1), 计算水汽压[16]:
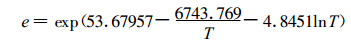
|
(1) |
式 (1) 中, T=t+273.16为绝对温标的露点温度 (单位:K); t为摄氏温标的露点温度 (单位:℃)。取t=td1可求得850 hPa的水汽压e1(单位:hPa)。
再利用式 (2), 计算比湿:
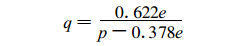
|
(2) |
将850 hPa的气压p1(单位:hPa) 和e1代入, 可得比湿q1(单位:kg · kg-1)。
2.2 求抬升凝结高度的要素先计算抬升凝结高度处的要素, 再计算气块的假相当位温。气块达到凝结高度前为干绝热过程, 位温和混合比守恒。其中, 位温守恒可表示为
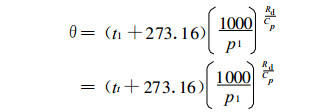
|
(3) |
可计算试解高度pt(单位:hPa) 的试解温度tt(单位:℃):
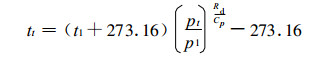
|
(4) |
其中, Rd为干空气比气体常数, 取为287J ·kg-1 · K-1; Cp为定压比热, 取为1004J · kg-1 · K-1; 下标t表示试解变量, 下同, 其数值随迭代次数的增加而趋近于真值。
选取二分法的试解变量为气压, 在求解之前先用等距试解的方法来确定二分法的初始区间。在这个区间中, 由位温守恒求得下边界气压处温度对应的饱和比湿大于等于q1, 而上边界气压处饱和比湿小于等于q1。即用pb, pa分别表示下和上边界气压, 分别代入式 (4) 计算对应的温度tb和ta, 用式 (1) 和 (2) 求得qb和qa。确定二分法边界的条件为qb≥q1, qa≤q1。等距试解的步长取为100 hPa。
二分法迭代边界确定后, 用qt试解。由式 (4) 计算试解温度, 再由式 (1) 和 (2) 依次求得试解水汽压et和比湿qt。比较qt与q1的关系, 刷新迭代边界。取二分法的精度ε=0.01 hPa, 满足精度条件可得抬升凝结高度处的要素值, 即p1=pt, t1=tt, e1=et。由于比湿守恒, 即q1=q1, 这样可计算抬升凝结高度处的假相当位温:
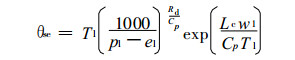
|
(5) |
式 (5) 中, Tl=tl+273.16为抬升凝结高度处的温度 (单位; K); el为抬升凝结高度处的水汽压 (单位: hPa)。由式 (2) 的逆函数和ql计算, 以减少误差。在式 (5) 中,
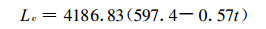
|
(6) |
Lc为凝结潜热 (单位:J · kg-1)。在抬升凝结高度处t=tl,
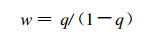
|
(7) |
式 (7) 中, w为混合比 (单位:kg · kg-1)。在抬升凝结高度处ql=q1, w=w1。
2.3 计算500 hPa的气块温度和沙瓦特指数先对沙瓦特指数的存在性进行判断, 如果2.2节中计算的抬升凝结高度处气压小于500 hPa, 即pl < p2, 表明气块抬升到500 hPa的过程为干绝热过程。这时有两种选择:一是从严格意义上说, 此时的沙瓦特指数没有定义, 算法返回这一信息, 结束计算; 二是对沙瓦特指数的定义进行扩展, 使之包括这一种类型。对于第二种情况, 可由式 (4) 计算500 hPa的气块温度ts0。由于气块上升为干绝热过程, 此时环境温度与气块温度的差定义为干沙瓦特指数:
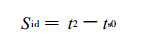
|
(8) |
因为上升过程中位温守恒, 且位温和温度成正比, 即式 (8) 等价于∂θ/∂z表示的大气稳定状况。此时式 (8) 表示的大气稳定性质与沙瓦特指数一致, 且在量值上有连续性。在功能上可将其与传统定义的沙瓦特指数视为同一物理量, 以减少其定义域上的局限性。
当pl > p2时, 气块的上升过程中包括湿绝热过程, 称之为湿沙瓦特指数。此时根据假相当位温守恒的原理, 采用二分法迭代计算500 hPa处的气块温度。选取迭代的变量为温度。在T-lnp图上, 干绝热线的坡度比湿绝热线坡度小, 在湿绝热上升过程中气块温度tt总是小于起始高度处温度, 即ts0≤tt≤tl, 从物理上可取二分法的初始迭代区间为[ts0, tl]。
每次迭代气压取固定值p2, 由试解温度tt依次计算。由式 (1) 计算试解水汽压et, 式 (2) 计算试解比湿qt, 式 (6) 计算试解凝结潜热Lc, 式 (7) 计算试解混合比wt, 再由式 (9) 求取试解的假相当位温:
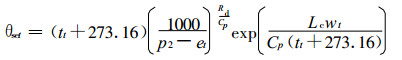
|
(9) |
比较试解假相当位温与抬升凝结高度处的假相当位温来刷新边界, 选取精度条件为ε=0.01 ℃。满足精度条件的试解温度就是500 hPa的气块温度, 即ts=tt。用500 hPa环境温度减去气块温度得到湿沙瓦特指数:
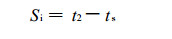
|
(10) |
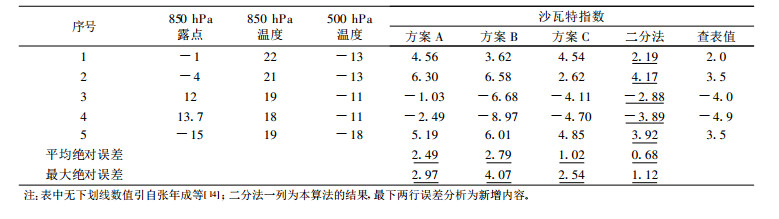
张年成等[14]对沙瓦特指数的计算方法进行探讨, 并对3种计算方案进行比较 (表 1)。根据同样的数据, 采用二分法迭代计算的结果也列入表 1。表 1还给出了误差分析结果。误差分析的真值取为最末一列“查表值”所表示的查表或点绘得到的沙瓦特指数。由表 1可见, 不同方案计算的沙瓦特指数有较大差异; 二分法的平均绝对误差和最大平均误差在4个方案中最小, 说明二分法计算精度达到较高水平。其中, 二分法的计算方案与方案A最类似, 但也存在3点不同:二分法用迭代法计算抬升凝结高度处的要素, 而方案A采用经验公式计算; 二分法用非等距迭代计算假相当位温守恒过程中的气块温度, 而方案A采用的是等距试解方法; 二分法的计算方案中假相当位温的表达式考虑了水汽压和混合比[16] (如式 (9)), 而方案A中没有考虑水汽压, 混合比用比湿来代替, 即二分法的假相当位温公式更加精确。
|
|
表 1 多站点计算的沙瓦特指数及其与查表或点绘求得的沙瓦特指数对比 (单位:℃) Table 1 Comparison between Showalter indexes computed by bisection method and those by table/chart interpolating at multi-stations (unit:℃) |
采用二分法计算的沙瓦特指数达到了一定精度 (表 1), 但是判别的样本数只有5个, 还可能存在代表性不足的问题。也就是说, 该计算方案可能存在适用性的“盲区”。从沙瓦特指数的定义看, 计算沙瓦特指数的核心问题是计算500 hPa的气块温度, 该气块温度是850 hPa温度和露点的函数, 这正是用查表法计算沙瓦特指数的核心依据。因此, 可通过二分法能否成功再现500 hPa气块温度查算表来判断其适用性。
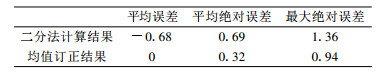
3.2 与查表法的比较查表法的基本流程是, 给定850 hPa温度和露点, 由查算表来查取并插值得到相应的500 hPa气块温度, 再用实际500 hPa温度减去气块温度, 得到沙瓦特指数。查表法的基本工具是500 hPa气块温度查算表[13]。图 1给出了查表法和二分法的气块温度及其差值, 其中图 1a为查算值[13], 图 1b为二分法计算的气块温度, 图 1c为二分法计算值与查算值之差。为了给出两种方法差别的主要特征, 对图 1c等值线进行了九点平滑。由图 1a和图 1b可见, 在查算表的定义区间中, 气块温度随温度露点差的增加而减小, 随温度的增加而增加, 两者的分布型是一致的。以查表值为“真值”, 二分法计算的气块温度误差在整个定义区间中总体上为负值。表 2给出了未平滑的二分法计算结果与上述“真值”误差分布统计特征, 其中二分法的平均绝对误差为0.69 ℃, 平均误差为-0.68 ℃, 两者在量值上接近, 表明二分法的计算误差以系统性误差为主。取t′s=ts+0.68作为均值订正, 二分法订正后的平均绝对误差和最大绝对误差都有所减少。计算结果中, 仅查算表最右上的一个格点是干沙瓦特指数, 其他都为湿沙瓦特指数, 表明二分法与查表法所得气块温度的对比主要反映了湿沙瓦特指数的情况。由于二分法计算的气块温度偏低, 使得计算的沙瓦特指数偏高。
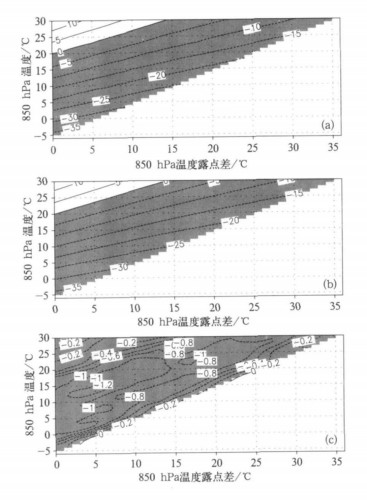
|
|
| 图 1. 二分法与查表法计算的500 hPa气块温度对比 (a) 查表法, (b) 二分法, (c) 二分法与查表法的差值 (阴影区:负值) Fig 1. 500 hPa parcel temperatures computed by table interpelating methods (a) and bisection (b), and their differences (c) (shaded region:negative value) | |
|
|
表 2 以查表法为参照二分法及其均值订正后计算的500 hPa气块温度的统计对比 (单位:℃) Table 2 Statistical error features of 500 hPa parcel temperatures computed by bisection and its mean value correction referring to those of table interpolating (unit:℃) |
需要指出的是, 从查算值 (图 1a) 的气块温度分布特征看, 也可采用简单的二元函数拟合计算, 并能达到较高精度。但是, 二元函数拟合的物理意义不清楚, 且仅适用于沙瓦特指数所定义的两个气层间的绝热抬升过程, 可移植性较差。而二分法物理意义清晰, 可用于计算任意起始高度上升到任意目标高度处绝热抬升的气块温度, 通用性较强。
二分法计算的气块温度会一致性偏小的主要原因可能是, 没有考虑气块上升过程中对水滴的夹卷作用。由湿绝热过程的定义可知, 气块上升过程中水汽凝结, 留下凝结潜热后, 水滴脱离气块形成降水。若大气严格按照上述物理模型演变, 天空中将没有云, 只有上升气流和降水, 这与实际状况有差别。若考虑到云的因素, 则必须考虑上升气流对水滴的夹卷作用。在湿绝热抬升过程中, 气块温度随高度递减, 在低层脱离的水滴具有较高的温度, 而在高层脱离的水滴具有较低的温度, 但都高于到达目标高度 (500 hPa) 时的气块温度, 若将这些水滴收集起来, 与到达目标高度的饱和气块构成一个封闭系统, 则会得到一个平衡的温度。该平衡温度略高于不考虑夹卷作用的气块温度, 且水汽越多、抬升凝结高度越低, 平衡温度高于气块温度的值越大。有关水滴夹卷作用的热力效应可以部分解释计算结果系统性偏小的原因。从上述过程看, 计算的误差值应该随850 hPa温度露点差的增加而减少。由误差分布 (图 1c) 可见, 850 hPa温度为-5~10 ℃区间, 对应的误差值与之相符, 但是11~30 ℃区间的误差分布随温度露点差的增加有一个先增后减的过程, 上述物理机制仅能部分解释该分布特征。由此可见, 考虑上升运动对水滴的夹卷作用, 相当于在气块内部增加了一个热源。该热力作用可以部分解释引起误差的原因。除此之外, 计算精度还受其他因素的影响, 如基本经验公式差别以及查表值本身的误差分布等。
4 结论与讨论在沙瓦特指数的计算方案中引入二分法。与其他方案比较表明, 该方案的计算精度有所改善。为了进一步确定该计算方案的适用性和误差分布特点, 与查表法计算的气块温度进行了对比, 结果表明, 该算法与查表法的最大绝对误差为1.36 ℃, 平均绝对误差 (0.69 ℃) 和平均误差 (-0.68 ℃) 在数值上接近, 表明两种算法以系统性偏差为主。造成500 hPa气块温度计算结果系统性偏低的原因, 可通过上升气流对水滴夹卷的加热作用得到部分解释。
因为涉及气块温度计算的问题, 上述算法具有较好的应用前景, 可用于计算沙瓦特指数[1]、改进的沙瓦特指数[4-5]、抬升指数[7-11]及与气块温度廓线相关的积分类稳定度指数。后者主要有对流有效能量 (CAPE) 指数[17]和对流抑制能量 (CIN) 指数[18]。需要指出的是, 当计算湿绝热过程气块温度垂直廓线具有较高分辨率时, 自下而上计算气块温度可用上一步计算的气块温度代替2.3节中初始迭代区间的上界, 由于二分法的计算次数对初始迭代区间的宽度具有依赖性, 此时起始迭代区间较小使得二分法计算步骤减少。Schaefer[2]在肯定稳定度指数可用性的同时, 强调没有哪一个指数能“完美”描述强雷暴潜势。一般而言, 一个稳定度指数只能反映对流活动的一个或几个方面, 但也并非反映的方面越多就越好。例如, Haklander等[11]对32个对流指数在荷兰的适用性进行了研究, 结果表明, 具有近地面层100 hPa厚度平均属性气块的抬升指数效果最好, 而该指数仅反映了低层到对流层中层 (500 hPa) 的不稳定状况, 与之形成鲜明对比的是, 瑞士指数[6]和强风暴威胁指数 (SWEAT)[19]尽管考虑不稳定的较多方面 (如包括了风的作用), 但其效果却有限。影响对流活动的因素很多, 例如地理位置就是一个重要因素[20]。这些表明, 稳定度指数的适用性是需要进一步研究的问题。
| [1] | Showalter A K, A stability index for thunderstorm forecasting. Bull Amer Meteoro Soc, 1953, 34: 250–252. |
| [2] | Schaefer J T, Severe thunderstorm forecasting: A historical perspective. Wea Forecasting, 1986, 1: 164–189. DOI:10.1175/1520-0434(1986)001<0164:STFAHP>2.0.CO;2 |
| [3] | 刘健文, 郭虎, 李耀东, 等. 天气分析预报物理量计算基础. 北京: 气象出版社, 2005: 77-86. |
| [4] | Curtis R C, Panofsky H A, The relation between large-scale vertical motion and weather in summer. Bull Amer Meteor Soc, 1958, 39: 521–531. |
| [5] | Hovanec R D, Horn L H, Static stability and the 300 mb isotach field in the Colorado cyclogenesis area. Mon Wea Rev, 1975, 103: 628–638. DOI:10.1175/1520-0493(1975)103<0628:SSATMI>2.0.CO;2 |
| [6] | Huntrieser H, Schiesser H H, Schmid W, et al. Comparison of traditional and newly developed thunderstorm indices for Switzerland. Wea Forecasting, 1997, 12: 108–125. DOI:10.1175/1520-0434(1997)012<0108:COTAND>2.0.CO;2 |
| [7] | Galway J G, The lifted index as a predictor of latent instability. Bull Amer Meteor Soc, 1956, 37: 528–529. |
| [8] | Prosser N E, Foster D S, Upper air sounding analysis by use of an electronic computer. J Appl Meteor, 1966, 5: 296–300. DOI:10.1175/1520-0450(1966)005<0296:UASABU>2.0.CO;2 |
| [9] | Peppier R A, Lamb P J, Tropospheric static stability and central North American growing season rainfall. Mon Wea Rev, 1989, 117: 1156–1180. DOI:10.1175/1520-0493(1989)117<1156:TSSACN>2.0.CO;2 |
| [10] | Sanders F, Temperatures of air parcels lifted from the surface :Background, application and nomograms. Wea Forecasting, 1986, 1: 190–205. DOI:10.1175/1520-0434(1986)001<0190:TOAPLF>2.0.CO;2 |
| [11] | Haklander J, Delden A V, Thunderstorm predictors and their forecast skill for the Netherlands. Atmos Res, 2003, 67-68: 273–299. DOI:10.1016/S0169-8095(03)00056-5 |
| [12] | Gary L A, Peter H H, Paul T S, et al.Atmospheric Sciences Section Illinois State Water Survey Final Report, Illinois Precipitation Enhancement (Phase Ⅰ), Design and Evaluation Techniques for High Plains Cooperative Program, 1977. |
| [13] | 寿绍文, 励申申, 王善华, 等. 天气学分析. 北京: 气象出版社, 2002: 179. |
| [14] | 张年成, 朱俊峰, 陈红萍, 等. 沙氏指数计算方案探讨. 气象科技, 2007, 35, (2): 171–174. |
| [15] | 乔全明, 阮旭春. 天气分析. 北京: 气象出版社, 1988: 41-75. |
| [16] | Emanuel K A, Atmospheric Convection. New York: Oxford University Press, 1994: 329-391. |
| [17] | Moncrieff M W, Miller M J, The dynamics and simulation of tropical cumulonimbus and squall lines. Quart J Roy Meteor Soc, 1976, 102: 373–394. DOI:10.1002/(ISSN)1477-870X |
| [18] | Colby Jr F P, Convective inhibition as a predictor of convection during AVE-SESAME Ⅱ. Mon Wea Rev, 1984, 112: 2239–2252. DOI:10.1175/1520-0493(1984)112<2239:CIAAPO>2.0.CO;2 |
| [19] | Miller R C.Notes on Analysis and Severe Storm Forecasting Procedures of the Air Force Global Weather Center.Tech Rep 200(Rev).AWS:U S Air Force, 1972. |
| [20] | Jacovides C P, Yonetani T, An evaluation of stability indices for thunderstorm prediction in Greater Cyprus. Wea Forecasing, 1990, 5: 559–569. DOI:10.1175/1520-0434(1990)005<0559:AEOSIF>2.0.CO;2 |
 2009, 20 (4): 486-491
2009, 20 (4): 486-491