应用气象学报  2009, 20 (3): 329-336   PDF    
引用本文
杨磊, 杨忠东. 极轨气象卫星自动地标导航方法[J]. 应用气象学报, 2009, 20(3): 329-336.
Yang Lei, Yang Zhongdong. The Automated Landmark Navigation of the Polar Meteorological Satellite[J]. Journal of Applied Meteorological Science, 2009, 20(3): 329-336  
极轨气象卫星自动地标导航方法
杨磊, 杨忠东     
中国气象局中国遥感卫星辐射测量和定标重点开放实验室 国家卫星气象中心，北京 100081
2008-05-29 收到, 2008-12-26 收到修改稿.
资助项目: 国家自然科学基金青年科学基金项目（60702040）和科技部科技支撑项目（科技部科技支撑项目）共同资助.    
摘要: 该文实现了一种极轨气象卫星的自动地标导航方法。地标导航能够纠正由于姿态而引起的定位误差。首先根据当前轨道遥感卫星图像中海洋、陆地、河流等地物特征能量的概率分布情况，利用全球模板，建立地标库，然后通过最大相关系数方法计算地标偏移量，从而获得姿态偏差，之后利用计算得到的姿态偏差对遥感卫星图像重新导航，获得地理定位结果。利用FY-1D扫描辐射计的遥感数据对方法进行检验，结果表明：该文所提出的自动地标导航方法可以有效纠正由姿态而引起的定位误差，达到像素级的定位精度。该方法能够突破传统地标导航方法需要丰富的遥感卫星历史资料的限制，拓展传统地标导航方法的适应范围。该方法已在我国2008年5月发射的新一代极轨气象卫星FY-3号上得到应用，并将在下一代静止轨道气象卫星FY-4号上进一步开发。
关键词: 自动地标导航    气象卫星    地理定位    
The Automated Landmark Navigation of the Polar Meteorological Satellite
Yang Lei, Yang Zhongdong     
Key Laboratory of Radiometric Calibration and Validation for Environmental Satellites, National Satellite Meteorological Center, China Meteorological Administration, Beijing 100081
Abstract: The problem of automated landmark navigation for the polar meteorological satellite is addressed. Automated landmark navigation can correct the systematic image navigation errors due to orbit, attitude and alignment matrix disturbance. Traditional automated landmark navigation methods need selecting the base image from long time series satellite imagery; otherwise it can result in registration displacements. Previous methods have shown that having daytime and nighttime (including early morning) base images for each season can minimize the registration error. The processing of one year data would thus require a minimum of eight base images for each location, and it limits the method from being widely applied. There are great needs for an accurate, easily implemented navigation system capable of automated landmark navigation when long time series satellite imagery data are absent. First, cloud detection methods insure that contamination from cloudy pixels is minimized. Second, the base image is composed of content features and structural features. The content features are constructed from the energy distribution of the current satellite image's ocean, land, rivers and so on. By defining the landmark feature point, the landmark's structural features are constructed from the global template. The landmark content and structural features are combined together to form the full base image. Third, the maximum cross correlation (MCC) method produces displacement vectors, which are translated into satellite attitude corrections to be added to the orbital image navigation corrections. Each resulting displacement vector has a correlation coefficient, which quantifies how well a pattern is matched. Displacements with correlations lower than the 95% confidence value is the elimination of error matching. The image navigation accuracies are also closely related to the landmark spatial distribution. The image navigation corrections are more accurate when the landmarks are average distributed through the whole satellite image. Finally, FY-1D satellite data are used to assess the performance. The testing results shows that this method is automatic and is successful to rectify the image navigation errors due to attitude disturbance and the rectified errors are within one pixel. This method does not use long time cache files needed by early methods and thus extend the applicability. The proposed method has been applied in Chinese next generation polar meteorological satellite FY-3 and will be developed further in the next generation geostationary meteorological satellite FY-4.
Key words: automated landmark navigation     meteorological satellite     image navigation    
引言

极轨气象卫星是我国天基观测系统的一个重要组成部分, 它所获得的资料不仅在天气系统分析和天气预报中显示出独特的能力和作用, 而且其应用范围已扩展到气候、自然灾害监测、海洋、水文、植被以及地球环境的动态监测等领域。我国已于2008年5月发射第二代极轨气象卫星———风云三号 (简称FY-3号), FY-3号采用三轴稳定方式, 它是在风云一号 (简称FY-1号) 气象卫星技术基础上的发展和提高, 在功能和技术上都向前跨进了一大步。FY-1号和FY-3号都搭载可见光红外扫描辐射计, 星下点分辨率为1.1 km。

遥感卫星热变形、太阳光压、设备老化、仪器安装误差等多种因素都会引起卫星姿态 (俯仰、滚动和偏航) 发生变化, 从而使得遥感仪器扫描镜指向随之变化, 导致遥感卫星图像产生不同程度的几何失真, 最终对于遥感定量产品反演和卫星遥感应用效果的提高以及卫星整体性能的发挥产生重大影响。为了修正在轨期间遥感仪器扫描境的指向偏差, 通常采用的方法是地标导航和恒星导航。本文主要介绍地标导航。FY-1号和FY-3号卫星搭载的可见光红外扫描辐射计, 共有10个通道, 星下点分辨率为1.1 km, 可以利用其遥感图像作为地标导航的依据。

自动地标导航非常必要。在地标导航方法研究初期, 研究人员通常采用人工选取地标, 进行交互式的地标导航工作[1-3]。这是一项需要高重复性、大劳动力的工作, 因此在大数据量的遥感卫星图像分析中, 交互式的地标导航变得不可行。同时, 更多遥感卫星图像的应用[4]需要对图像进行实时、自动处理, 因此人工选取地标变得更加不符合实际需要。同时, 交互式地标导航的另一个问题是准确性和一致性。人工选取地标具有很高的主观性, 不同人员所选择的地标会有所不同, 使得地标导航缺少一致性且其准确性过多依赖于工作人员的经验, 由此引起的导航误差能够严重影响后续的遥感应用。在文献[5-6]中, 研究人员发现在图像导航上一个很小的误差能够对全局的遥感应用产生严重影响:一个小于0.2个像素的导航误差对后续的遥感应用产生了小于10%的误差。因此地标识别方法的自动性是未来地标识别方法所必须具有的特性。

国内外的研究人员对自动地标导航的方法进行了大量研究, 但由于历史资料积累等方面原因, 使得国外遥感卫星所采用的地标导航方法不适合于我国自主设计的气象卫星。对于地标导航来说, 其关键步骤在于地标识别, 只有准确识别地标, 才能够得到准确的地标偏移量, 从而有效地计算卫星姿态偏移量, 对遥感卫星图像进行导航。目前, 国际上的地标识别算法主要有:①基于地标重心的识别方法; ②基于边界的匹配方法[7, 9-10]; ③直方图聚类方法[11]和最小方差方法[12]; ④基于特征的地标识别方法[4, 10, 13-19]。

Emery等[20]设计并实现了一种基于最大相关系数 (Maximum Correlation Coefficient, MCC) 的自动地标导航方法, 该方法是目前为止应用范围最为广泛的地标导航方法, 具有简单易于实现、计算速度快、高精度等优点, 但是需要专家根据大量历史资料制定模板库 (根据不同季节, 白天、夜间的模板不一样)。而对于象我国这样遥感卫星对地探测资料并不丰富的国家并不可行。Taejung等[21]试图采用Emery等的方法实现GOES卫星的地标导航, 但是提出“MCC方法不适用”, 这是由于待匹配模板的细节信息量不够造成的。国内的研究人员针对遥感卫星地标导航方法也开展了大量研究工作, 但是多基于人工交互式方法[22-23]。

鉴于上述原因, 本文设计并提出一种适用性更加广泛的高精度自动地标导航算法:首先通过学习当前轨道遥感卫星图像中海洋、陆地、河流等地物特征能量的概率分布情况, 然后利用全球模板建立地标库, 利用最大相关系数方法计算地标偏移量, 获得姿态偏差, 之后利用计算得到的姿态偏差对遥感卫星图像重新导航, 获得地理定位结果, 完成地标导航。最后, 利用FY-1D扫描辐射计的遥感数据进行测试, 验证算法的可行性以及精度。

1 地标导航

在遥感卫星图像导航与定位过程中, 地球曲率、地球旋转以及卫星的姿态变化都可以引起定位误差。遥感卫星图像导航与定位的一般过程是首先假设姿态偏差为零, 然后根据遥感仪器的扫描方式、遥感仪器与卫星的安装关系以及卫星轨道数据对所获得遥感卫星图像进行地理定位。此时, 获得了地标的地理经纬度, 计算其与标准地理经纬度的差异, 通过地标偏移量计算姿态的偏差, 然后对遥感卫星图像进行重新定位, 获得准确的地理经纬度。

对卫星姿态的计算首先要确定地标偏移量, 然后计算姿态角。采用最大相关系数方法计算地标偏移量。研究人员[20, 24]在计算地标偏差过程中, 成功地应用了MCC方法, 但是需要手工制定大量的地标模板[20]。这对于象我国这样尚未整理出大量可用于地标导航资料的国家来说, 尚不可行。

Rosborough等[8]详细介绍了估计姿态偏差的方法, 为了获得准确的姿态, 该方法需要至少2个地标。应用该方法的一个前提是, 在获取遥感卫星数据过程中卫星姿态保持不变; 另一个前提是, 卫星轨道参数的预报或者实时测量是准确的。如果卫星的轨道参数预报或者实时测量数据不正确, 那么导航所产生的误差会转嫁给姿态, 主要是姿态的俯仰分量。

地标的选取对于姿态偏差的计算非常重要, 如果集中在一个区域, 很容易影响姿态偏差计算的准确性。地标应该尽量平均分布于遥感卫星图像, 并且尽量分布于星下点两侧。

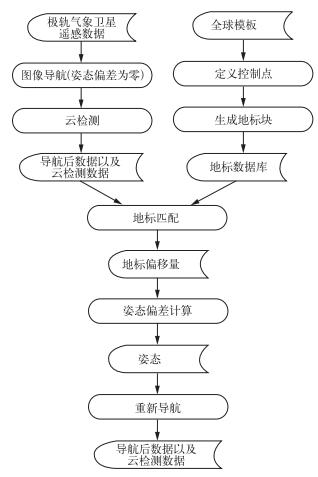
需要指出的是, 云对于地标导航的影响非常大, 能够严重降低地标导航的精度, 因此在进行地标导航之前, 需要进行非常严格的云检测。自动地标导航的流程如图 1所示。

图 1. 自动地标导航流程 Fig 1. Flowchart of the automated landmark navigation process

1.1 地标匹配

最大相关系数方法是地标匹配方法中应用范围最广的方法, 具有运算速度快、准确率高等特点, 并且已经在NOAA系列卫星中得到了业务化应用[20]。因此, 本文也采用MCC方法进行地标匹配。MCC方法曾经用于计算静止气象卫星的云运动检测[25]以及序列光学和微波图像分析中[26-27]。它的原理相对简单。给定一幅图像f (x, y), 最大相关问题就是在该图像中寻找与实现给定的模板图像w (x, y) 相匹配的位置。将w (x, y) 作为一个空间滤波器在f (x, y) 中的每个位置计算w与f的乘积的和, 然后归一化, 如下:

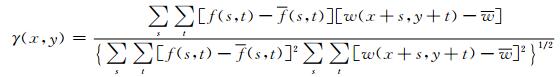
(1)

w (x, y) 在f (x, y) 中的最佳匹配是在得到的相关图像中出现最大值的地方。由于计算量较大, 一个变通的方法是可以将其与卷积联系起来, 如:

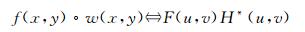
(2)

式 (2) 中, 。表示相关运算, *表示复共轭, F, H是傅立叶算子。

地标成像空间分辨率较低、云污染、耀斑、遥感图像边缘形变等因素都对所产生的MCC系数有很大影响, 使得所获得的最大相关系数不是很高, 并由此而产生大量的误匹配。为了减少误匹配问题的影响, 可以采用假设检验的方法。这就要求地标模板图像在遥感卫星图像的搜索区域内进行滑动时, 遥感卫星图像的搜索区域必须足够大 (在允许的运算时间内, 尽可能大), 以使得产生的一系列相关系数值具有统计特性, 应用t-检验, 所有小于显著水平0.05 (对应的相关系数值约为0.72) 的匹配都作为误匹配。云对于地标匹配的影响非常大, 可以产生很多的误匹配。为了减少云对于地标导航的影响, 本方法要求待匹配的遥感卫星图像区域上空是无云的。

需要注意的是, 在使用MCC方法进行地标匹配之前, 需要确定模板图像与地标成像是否是同一个投影方式。文中试验所使用的云图是轨道投影方式, 在匹配之前, 需要将全球模板转换为轨道投影方式。

1.2 地标库生成以及云检测

地标库生成直接影响到地标匹配的准确性, 从而对姿态偏差的计算产生重大影响。为了最终提高姿态计算的准确性, 文献[20]中提到, 对于每一个地标, 需要建立至少8个模板 (白昼、黑夜、春、夏、秋、冬), 这样在建立模板过程中就会花费大量时间。同时, 对于像我国这样遥感卫星资料尚不丰富的国家, 该方法是不适用的, Taejung[21]等的研究结果也证明了这点。本文所使用的全球模板来自于IMAPP软件包。该全球模板基于世界海岸线矢量库 (World Vector Shore-line) 以及世界数据银行 (World Data Bank)。分辨率是1 km等经纬度分布。

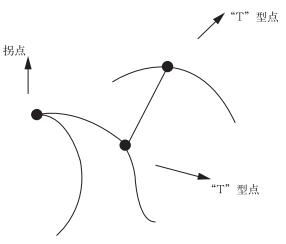
地标库实际上就是由若干个一定大小的地标组成的。这些地标图像具有显著的地物特征, 大多是湖泊、河流、海岸线、岛屿等, 具有清晰的结构特征。地标图像可以由地面控制点生成, 如下定义地面控制点:地标轮廓的拐点、“T”型连接点或者其他高曲率点 (见图 2)。

图 2. 地面控制点定义 Fig 2. Definition of ground control point

为了提高姿态计算的准确性, 在自动计算地面控制点后, 可以人工对这些自动计算得到的地面控制点进行选择, 这样既比原先手工选择地标模板快速, 同时又提高了准确性。

在确定地面控制点之后, 以其为中心, 自动扩展成一定大小的地标块 (文中所采用的大小是17×17)。地标图像每一个像素的经纬度可以从全球模板中计算得到。在得到地标块的结构信息后, 应该对其进行填充, 丰富其细节信息, 增加匹配的准确性。具体过程如图 3, 按照下面的步骤进行:

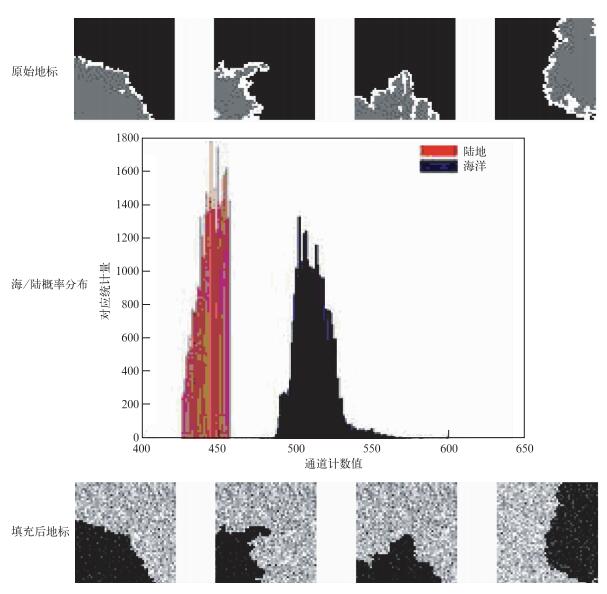
图 3. 地标生成过程 (其中海/陆槪率分布采用的数据是2005年6月20日23:37 (世界时) FY-1D扫描辐射计第4通道数据) Fig 3. Examples of landmark whose energy distribution data is from the FY-1D scanning radiomoter 4th band data at 23:37 20 June 2005

① 根据全球模板图像以及地标的特征点定义, 获得地标的结构信息 (下称地标结构)。

② 根据“初级定位” (姿态为零) 的结果, 可以获得遥感图像中地标模板的一个初始位置; 同时, 根据“初级定位” (姿态为零) 的结果, 对于每个像素, 判断是陆地、海洋还是河流。

③ 以步骤②中获得的下垫面类型为索引, 统计概率分布情况。

④ 根据步骤③获得的概率分布情况, 填充到步骤①获得的地标结构中 (仍然是以下垫面类型为索引, 不同的下垫面类型填充的数据是不同的), 获得完整的地标模板。

云对于地标匹配的结果影响很大, 它可以使得MCC方法在匹配过程中产生大量的误匹配。文中的原则是如果地标上空存在云污染, 那么该地标舍弃不用。本文采用国家卫星气象中心L2级云检测产品数据。云检测方法是动态阈值的方法, 具体方法可参考技术报告①。业务系统中的云检测算法是多特征阈值方法, 其中多特征包括红外和可见光单通道特征, 通道差特征和通道比值特征等。各个特征阈值的确定主要采用直方图动态阈值方法、利用正演模拟数据集统计获取方法以及通过理论分析和经验获取方法, 阈值获取方法在技术报告中有详细叙述。在单通道云判识的基础上, 通过分析给出多通道特征综合云检测方案, 最后输出结果是各个像素点的云检测判识结果, 以及云和晴空判识的可信度。

① 师春香, 郑照军, 杨昌军, 等．FY-3/VIRR全球云检测算法及原型软件研发技术报告 (2007) (FY-3地面应用系统3-1) ．国家卫星气象中心．

1.3 姿态偏差计算

在得到地标偏移量后, 根据式 (3) 计算滚动、俯仰、偏航角。下面给出姿态角的定义, 首先定义轨道坐标系, 然后由此定义姿态角。轨道坐标系Rorb:轨道坐标系与卫星的位置和速度有关系。坐标系的原点在卫星质心, z轴方向是从卫星质心指向地心, y轴的方向由z轴方向与卫星瞬时速度方向矢量通过右手正交螺旋规则确定, x轴则是按照右手正交规则垂直于yoz平面。同时, 通常称x轴、y轴、z轴为滚动、俯仰、偏航轴。由此而产生的姿态角定义。滚动角ζr:俯仰轴与其自身在轨道水平面xoy上投影的夹角; 俯仰角ζp:滚动轴与平面xoy上投影的夹角; 偏航角ζy:滚动轴在平面xoy上的投影与轨道方向的夹角。卫星本体坐标系与姿态和轨道坐标系有关, 坐标原点在卫星质心, 首先, 绕轨道坐标系的z轴旋转ζy角; 其次绕x轴旋转ζr角; 最后绕y轴旋转ζp角, 得到卫星本体坐标系。

当可用的地标平均分布在遥感卫星图像, 并且位于星下点两侧时, 由此根据姿态偏差计算模型计算得到的姿态偏差 (滚动角、俯仰角、偏航角) 会更加准确。本系统采用的方法是, 尽量选择满足上述条件的一对地标, 计算姿态偏差 (ζr, ζp, ζy), 由此会产生多个姿态偏差值, 求其平均值作为最后的结果, 对遥感卫星图像进行重新导航。

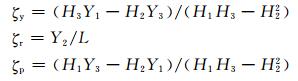
(3)

其中,

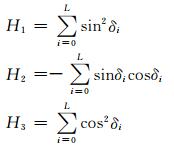
(4)

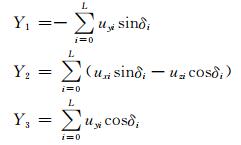
在卫星本体坐标系下求解方程 (3), 且δi是扫描角在卫星本体坐标系中的表达, uxi, uyi, uzi是单位观测向量分量在轨道坐标系中的表达[8]。

2 结果分析

应用文中的方法对2005年5—12月FY-1D扫描辐射计遥感数据 (62轨数据) 进行地标导航, 测试方法的导航性能。同时, 对于给定的n个未受云污染的明显目标, 如式 (5) 定义导航误差:

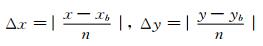
(5)

其中, x, y是应用文中介绍的地标导航方法后, 地标中心点在遥感图像中的坐标, xb, yb是在使用地标导航前, 地标中心点在遥感图像中的坐标。使用MCC方法 (采用阈值0.72) 进行地标匹配, 在导航前, 地标块的平均偏差是Δx=3.3, Δy=4.8 (每个像素对应空间分辨率1.1 km); 应用“自动地标导航”方法后, 地标块的平均偏差是Δx=1.0, Δy=0.9。由上述方法进行的定位误差控制在一个像素之内。

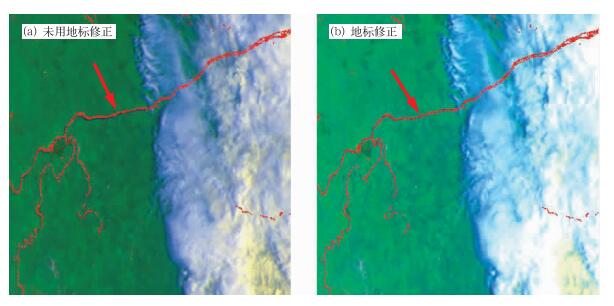
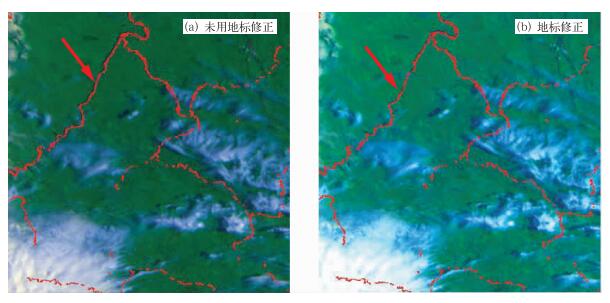
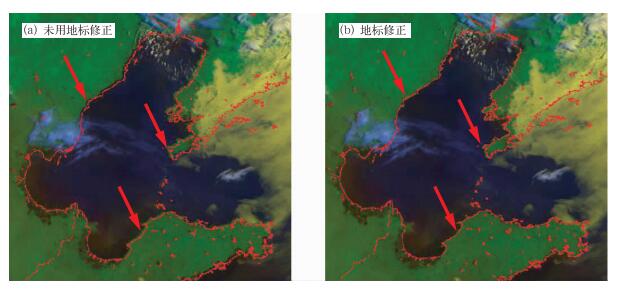
图 4a、图 5a、图 6a分别是俄罗斯奥廖克明斯克附近的勒拿河、阿尔丹河地区以及我国的渤海湾地区FY-1D扫描辐射计遥感图像, 如图中箭头所示区域, 红线是地理定位结果 (未使用地标导航), 与实际扫描成像的地物 (河流、海岸线) 存在明显偏差。以图 6a为例, 计算之后的滚动角是0.001222, 俯仰角是0.003289, 偏航角是0.002115。FY-1D的轨道高度是863 km, 滚动角或者俯仰角是0.00127时, 对应于星下点偏差1.1 km (1个像素)。在进行地标导航之后, 得到的定位结果如图 4b、图 5b、图 6b所示, 通过目视 (如箭头所示区域), 可以看到明显改善了定位的结果。

图 4. 俄罗斯奥廖克明斯克附近的勒拿河FY-1D扫描辐射计遥感图像定位结果 Fig 4. FY-1D scanning radiometer image navigation of Lena near Olokminsk in Russia

图 5. 俄罗斯阿尔丹河FY-1D扫描辐射计遥感图像定位 Fig 5. FY-1D scanning radiometer image navigation of Aldan River

图 6. 渤海湾地区FY-1D扫描辐射计遥感图像定位 Fig 6. FY-1D scanning radiometer image navigation of the Bohai Culf

3 讨论

本文通过分析当前轨道地标附近遥感图像能量分布特性, 构建准确的模板图像, 建立了一种适用性更加广泛的自动地标导航方法, 使得不需要人工干预就可以实现地标导航, 获得像素级的遥感图像地理定位结果。如其他地标导航方法一样, 本文提供的方法, 受到云的影响比较严重, 在后续工作中, 将致力于减弱云对于地标导航方法的影响。

致谢: 感谢国家卫星气象中心师春香研究员在云检测技术方面给予的帮助, 同时感谢国家卫星气象中心张里阳副研究员在地理投影方面给予的帮助。
参考文献
[1] Bachmann M, Bendix J. An improved algorithm for NOAA-AVHRRimage referencing. Int J Remote Sens, 1992, 13, (16): 3205–3215. DOI:10.1080/01431169208904111
[2] Ho D, Asem A. NOAA AVHRR image referencing. Int J Remote Sens, 1986, 7, (6): 895–904.
[3] Illera P, Delgado J A, Calle A. A navigation algorithm for satellite images. Int J Remote Sens, 1996, 17, (3): 577–588. DOI:10.1080/01431169608949028
[4] Jacqueline L M, William J C, Robert F C. An automated parallel image registration technique based on the correlation of Wavelet features. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40, (8): 1849–1864. DOI:10.1109/TGRS.2002.802501
[5] Townshend J, Justice C O, Gurney C, et al. The impact of misregistration on change detection. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30, (5): 1054–1060. DOI:10.1109/36.175340
[6] Dai X, Khorram S. The effects of image misregistration on the accuracy of remotely sensed change detection. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36, (5): 1566–1577. DOI:10.1109/36.718860
[7] Pergola N, Tramutoli V. SANA:Sub-pixel automatic navigation of AVHRR imagery. Int J Remote Sens, 2000, 21, (12): 2519–2524. DOI:10.1080/01431160050030619
[8] Rosborough G W, Baldwin D G, Emery W J. Precise AVHRR image navigation. IEEE Transaction on Geoscience and Remote Sensing, 1994, 32, (3): 644–657. DOI:10.1109/36.297982
[9] Pergola N, Tramutoli V. Two years of operational use of subpixel automatic navigation of AVHRR scheme:Accuracy assessment and validation. Remote Sens Environ, 2003, 85, (2): 190–203. DOI:10.1016/S0034-4257(02)00205-5
[10] Eugenio F, Marque S F. Automatic satellite image georeferencing using a contour-matching approach. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41, (12): 2869–2880. DOI:10.1109/TGRS.2003.817226
[11] Kuglin C D. Histogram-Based algorithms for scene matching. SPIE Infrared Technology for Target Detection and Classification, 1981, 302, (1): 99–107.
[12] Kuglin C D, Eppler W G. Map-matching techniques for use with multispectral/multitemporal data. SPIE Image Processing for Missile Guidance, 1980, 238: 146–156. DOI:10.1117/12.959141
[13] Li H, Manjunath B S, Mitra S K. A contour-based approach to multisensor image registration. IEEE Transactions on Image Processing, 1995, 4, (3): 320–334. DOI:10.1109/83.366480
[14] Dai X, Korran S. A feature-based image registration algorithm using improved chain-code representation combined with invariant moments. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37, (5): 2351–2362. DOI:10.1109/36.789634
[15] Djamdji J P, Bijaoui A, Maniere R. Geometrical registration of images:The multiresolution approach. Photogrammetric Engineering and Remote Sensing, 1993, 59, (5): 645–653.
[16] Zheng Q, Chellappa R. A computational vision approach to image registration. IEEE Transactions on Image Processing, 1993, 2, (3): 311–326. DOI:10.1109/83.236535
[17] Djamdji J P, Bijaoui A. Disparity analysis:A wavelet transform approach. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33, (1): 67–76. DOI:10.1109/36.368221
[18] Brown L. A survey of image registration techniques. ACM Computing Surveys, 1992, 24, (4): 325–376. DOI:10.1145/146370.146374
[19] Fonseca L M G, Manjunath B S. Registration techniques for multisensor sensed imagery. Photogrammetric Engineering and Remote Sensing, 1996, 62, (9): 1049–1056.
[20] Emery W J, Baldwin D G, Matthews D. Maximum cross correlation automatic satellite image navigation and attitude corrections for open ocean image navigation. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41, (1): 33–42. DOI:10.1109/TGRS.2002.808061
[21] Taejung K, Tae-Yoon, Hae-Jin C. Landmark Extraction, Matching and Processing for Automated Image Navigation of Geostationary Weather Satellites. Image Processing and Pattern Reconition in Remote Sensing II, Proceedings of the SPIE,2005:30-37.
[22] 卢耀秋. 静止气象卫星的地标导航计算方法. 计算物理, 1992, 9, (A02): 775–777.
[23] 赵礼铮, 白光弼. 极轨气象卫星局部数据集的精地标导航. 气象, 1992, 18, (11): 44–46.
[24] Walter E, David P, Marcus L, et al. GOES Landmark Positioning System. Proceedings of SPIE GOES-8 and Beyond, 1996, 2812: 789–804. DOI:10.1117/12.254124
[25] Leese J A, Noval C S, Clarke B B. An automated technique for obtaining cloud motion from geosynchronous satellite data using cross correlation. J Appl Meteor, 1971, 10, (1): 110–132.
[26] Emery W J, Thomas A C, Collins M J. An objective method for computing adjective surface velocities from sequential infrared satellite images. J Geophys Res, 1986, 91, (C11): 12865–12878. DOI:10.1029/JC091iC11p12865
[27] Ninnis R M, Emery W J, Collins M J. Automated extraction of pack ice motion from Advanced Very High Resolution Radiometer imagery. J Geophys Res, 1986, 91, (C9): 10725–10734. DOI:10.1029/JC091iC09p10725