水温是水环境最重要的影响因子之一, 水的物理、化学性质及水生生物、农作物对水温都很敏感, 水温的变化会对其产生较大影响。如水库水温分层可能直接导致库区内的水质分层和生态分层, 并且对水生生物、农田灌溉、工业供水、生活用水、下游河流的水质和生态平衡、以及库区水的利用 (养殖、娱乐) 等方面都产生重要影响, 同时水温的变化, 还对水工坝体温度应力分析、施工温控设计、继电机组冷却等也有重要影响, 因此对水库水温的研究具有重大的工程意义^[1-3]。

研究河道和水库的热输移规律一直是一个受到重视的课题^[4]。特别是生态环境的需要, 准确地预测研究水库建库后的库区水温结构和坝址下游水温的改变和影响更受到研究人员的关注^[5-7]。随着水利水电开发向西南山区转移, 将待建一大批山区巨型深水库, 由于电站下泄低温水对下游河道可能产生一定的生态影响, 邓云等^[7-11]基于统计学、流体力学、环境水力学和传热学理论建立了适用于大型深水库的立面二维水温热力模型, 并采用二滩水库原型观测资料对模型进行了验证, 深入揭示了水库水温分层和下泄水温的规律性和特点。研究发现^[12], 气象因素如太阳辐射、大气长波辐射、云量、相对湿度、风速等是影响水温热力模型的主要因素, 而太阳辐射和大气长波辐射对水气交界面热通量的贡献最大。在西南地区, 山川纵横, 群峦起伏, 河流走向曲折迂回, 各地气象条件变化很大。因此, 准确给出山区峡谷型深水库水温模型的气象要素边界条件, 对于准确模拟和预测山区水库库区水温结构和下泄水温有着重要的意义。

我国在山区气温的研究方面工作很多, 尤其以傅抱璞、翁笃鸣、沈国权等为代表的一大批学者总结出了一些山区气温推算方法, 例如分离综合法、回归余项法、成因分析法等。其中前两种方法最具代表性, 它们在理论上和实际处理上都比较合理, 目前在各地用得比较普遍。回归余项法所依据的原理与分离综合法一致, 在处理上最方便, 从前人应用的结果看拟合效果也较好^[13-16]。

回归余项法最早由沈国权^[13]提出, 认为在一个较大地区, 年、月平均气温的气候学方程是地理纬度ψ、经度λ和海拔高度h等因素 (认为这3个因素相关性不大) 的函数:

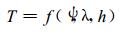
(1)

并将其用多元一次回归方程具体表示为:

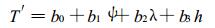
(2)

式(2)中, b₀为常数项; b₁, b₂, b₃为回归系数。式(1)是一个不考虑地形影响的温度理想化方程, 在实际工作中可由较大范围内各站资料通过回归分析建立起来。对于具体的山地测点, 作者认为山区测站总要受到地形影响, 除了已经考虑的因子外, 还应考虑地形影响项T_y, 于是考虑地形影响的山区温度方程为

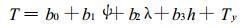
(3)

具体山区测点的地形影响项, 则为上面两式的差值:

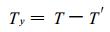
(4)

在比较山区各测点与按式 (1) 回归计算的理想化气温值后, 可绘制出计算区域的T_y分布图。在此基础上, 按式(3) 可确定计算区域任一山区测点 (ψ, λ, h) 的年、月平均温度。

此模型具体内容可参见文献[16]。

斜坡上的太阳直接辐射通量为:

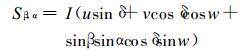
(5)

式(5)中, I为直接太阳辐射强度, ψ为地理纬度, δ为太阳赤纬, w为日照时角。

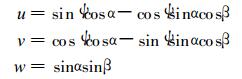
从研究地点始照时刻到终照时刻对时间t积分, 并利用卡斯特洛夫公式, 可得到在晴空情况下太阳直接辐射日总量的积分表达式:

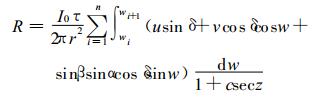
(6)

式(6)中, I₀为太阳常数, r为以日地平均距离为单位的日地距离。

进一步整理, 令c=0(相当完全透明大气或大气外界的情况), 便得到计算坡地和平地天文太阳直接辐射日总量的公式。

坡地:

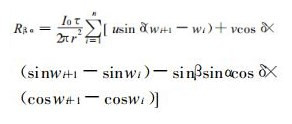
(7)

平地:

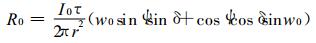
(8)

其中, 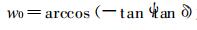为平地上的日照时角。

式(7)可以计算在晴空情况下任意方位坡地上的可能天文太阳直接辐射日总量, 直接利用这个公式来进一步推求坡地上任何一段时期内的可能直达太阳直接辐射总量的表达式较烦琐。傅抱璞在1958年曾经论证尽管当地坡面上的可能直接太阳直接辐射R_β,α与平地天文太阳直接辐射总量R₀相差很大, 但这二者的比值与当地水平面上的可能太阳辐射W与天文太阳辐射总量W₀的比值却总是近似相等的, 即

(10)

(11)

因为水平面上的天文太阳辐射W₀很容易由公式求得, 而其可能太阳辐射可直接计算或者有气象站实际观测资料可用, 参数f的值比较容易确定。因此利用式(11) 计算坡地上的可能太阳辐射总量简单、可行。

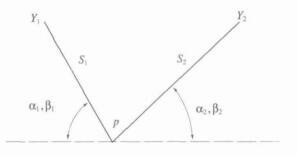
计算坡地上的可能太阳辐射总量的关键是得到坡地上的可照时角, 具体的求解方法与原则可参考文献[13]。山区河流与水库进行分段处理后, 各段的可照时角可近似用平行山脊求解可照时角方法来处理。当平行山脊Y₁, Y₂的长度远远大于二者之间的宽度, 且两山的高度变化不大时, 就可以用两个坡向相反 (设分别为β₁, β₂, 且|β₁-β₂|=180°) 的坡度为α₁, α₂的S₁和S₂坡面代替Y ₁和Y₂山体对水面上研究点P太阳照射的影响, 如图 1所示。近似地认为P点既在S₁坡面上, 又在S₂坡面上, 只有当S₁和S₂坡面能同时受到太阳照射时, P点才能受到照射。因此, S₁和S₂坡面开始同时受到太阳照射的时角和开始不能同时受到太阳照射的时角就是平行山脊中水面上P点的始照时角和终照时角, 两个坡面每天能同时受到太阳照射的时间就是P点的可照时间。

图 1

图 1. 平行山脊太阳辐射计算示意图 Fig 1. The calculation schematic diagram of solar radiation in parallel mountain ridges

雅砻江又名若水、打冲江、小金沙江, 是长江上游最大支流。它发源于青海省巴颜喀拉山西南麓, 上源叫扎曲, 流到甲衣寺后称雅砻江。按地貌特征划分, 甘孜以上可称上游, 甘孜至大河湾为中游, 大河湾以下为下游。雅砻江流域内地形异常复杂, 上游段地面为波状起伏的浑园山岭及缓坡, 河谷多为草原宽谷, 中游段地形切割越来越深, 河谷越来越窄, 特别是在雅砻江以下, 峭岩深谷紧密相间, 峰顶谷底高差达两、三千米, 盐源金河以下河段, 岸坡较为平缓, 江面逐渐开阔。

二滩电站位于四川省攀枝花市境内, 河段隶属雅砻江流域, 总装机容量330×10⁴ kW, 年发电量170×10⁸ kW · h。二滩电站坝址处多年平均流量为1640 m³/s, 库区地理范围为26.8°~27.8°N,101.7°~102.0°E。二滩挡水大坝为抛物线型双曲拱坝, 最大坝高240 m, 二滩水库回水长度超过140 km, 平均水面宽约400 m, 坝前最大水深超过200 m, 总库可容达58×10⁸ m³, 是一个典型的山区狭长型巨型深水库。

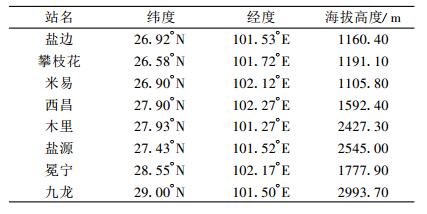
二滩水库河岸坡度取约30°, 库区主要走向为南北。根据库区走向和地形, 将库区分为九点八段。库区附近有盐边、攀枝花、米易、西昌、木里、盐源、冕宁、九龙等共8个气象站 (表 1) 及相应的多年平均逐月日照百分率和气温。采用攀枝花、米易、西昌、木里、盐源、冕宁、九龙7个站点进行温度方程拟合, 并用盐边气象站检验。

表 1

表 1 雅砻江流域气象站资料 Table 1 The climate data of Yalong River valley

表 1 雅砻江流域气象站资料 Table 1 The climate data of Yalong River valley

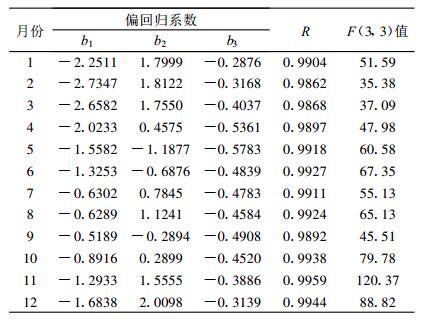
根据库区附近7个气象站的多年逐月月均气温拟合式(2), 得到的各项回归系数见表 2。在0.01显著水平下, F(3, 3)的临界值为29.46。各月的多元线性回归方程的F检验表明, 由附近气象站多年逐月平均气温拟合的F值都在35以上, 同时其复相关系数R均在0.98以上, 由此可见, 拟合方程的效果是显著的。表 2显示, b₁(温度随纬度的变化率) 全年都是负值, 表明各月温度都是随纬度的增加而降低, 呈冬春大夏秋小, 年变化十分显著, 12月-次年2月平均达到-2.22 ℃/纬度, 7-9月最低, 但是仍有约-0.60 ℃/纬度的变化。b₂ (温度随经度的变化率) 除5,6,9月为负值外其他月份都是正值, 总体上各月温度随经度的增加而增加, 年变化幅度较大, 12月-次年2月平均为1.87 ℃/经度, 最小值5-6月平均为-0.94 ℃/经度。b₃(温度随高度的变化率) 全年都是负值, 即各月温度都是随海拔高度的增加而降低, 年变化不大, 并比b₁, b₂变化小得多, 其绝对值仍然呈现冬小夏大的趋势。1月最小为-0.29℃/100 m, 4-5月最大平均约为-0.56℃/ 100 m, 年平均为-0.43℃/100 m。

表 2

表 2 雅砻江流域温度拟合方程的回归系数 Table 2 Partial regression coefficients of temperature equation in Yalong River valley

表 2 雅砻江流域温度拟合方程的回归系数 Table 2 Partial regression coefficients of temperature equation in Yalong River valley

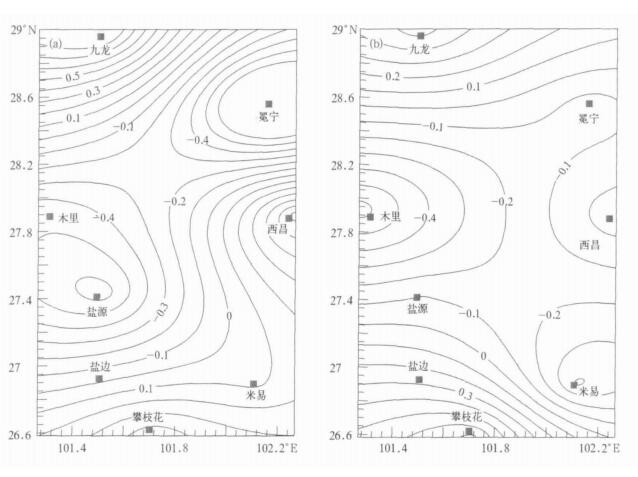
采用式(3)计算得到雅砻江流域大地形温度订正值的地理分布。图 2列出了4月、8月的地形影响项等值线图。由图 2可知, 城区气象站地势较周围低平, 太阳辐射和大气辐射增热后不易扩散和交换, 地形影响项起增温作用, 诸如攀枝花、九龙、西昌等气象站, 全年的地形影响项均为正值。山区气象站所在地形复杂, 因此地形订正项根据季节和地势变化有正有负。同时, 由图 2可以看出, 二滩库区范围主要在木里、西昌、米易、攀枝花和盐源之间, 地形影响在库尾与库首间有所差异。

图 2

图 2. 雅砻江流域4 月(a)、8 月(b)大地形温度订正图(单位: ℃) Fig 2. Temperature effect of macrotopography of Yalong River valley in April (a)and August (b) (unit: ℃)

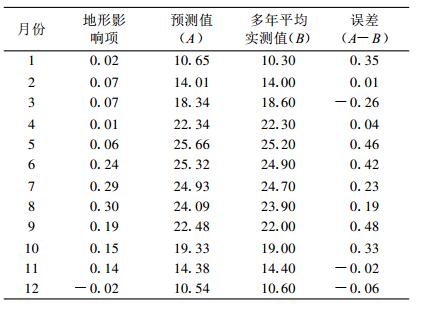
采用偏回归系数(表 2)并用式(2)对盐边气象站的多年逐月平均气温进行检验。表 3列出了全年各月的地形影响值和预测结果, 检验精度都在0.5 ℃以内。盐边气象站三面环山, 地形影响项起增温作用。夏季预报精度平均偏大0.3 ℃左右, 主要是由于盐边气象站处于二滩库区内, 大水体降温所致。

表 3

表 3 盐边气象站气温验证效果(单位: ℃) Table 3 Verification effect of temperature on weather station of Yanbian(unit: ℃)

表 3 盐边气象站气温验证效果(单位: ℃) Table 3 Verification effect of temperature on weather station of Yanbian(unit: ℃)

表 4是二滩库区的气温推算结果。随着纬度的增加, 库区各月的气温是逐渐减小的。库尾与库首的差值年平均在1.6 ℃左右, 2月与3月差值最大, 均约2.7 ℃。库区沿库尾至库首, 气温沿程增加, 这与流域气候变化特征是一致的。

表 4

表 4 二滩库区的气温推算结果 (单位: ℃) Table 4 The result of temperature calculated of Ertan reservior from the method (unit: ℃)

表 4 二滩库区的气温推算结果 (单位: ℃) Table 4 The result of temperature calculated of Ertan reservior from the method (unit: ℃)

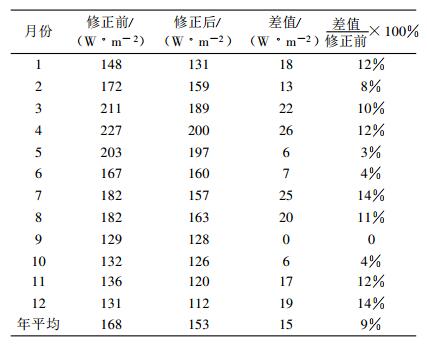
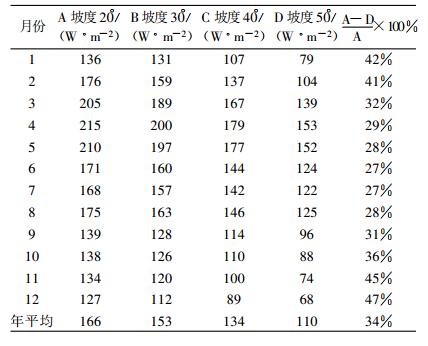
表 5列出了修正前后二滩水库库区水面接受的太阳辐射数据。库区水面接受的太阳辐射数据利用九点八段的段数值经过长度加权算得。修正前太阳辐射年平均在168 W/m²左右, 最高值出现在4月, 月平均达到227 W/m², 最低值出现在9月, 月平均只有129 W/m²。升温期3~5月, 月平均太阳辐射在213 W/m²;降温期10月-次年1月, 月平均太阳辐射为138 W/m²。修正后的太阳辐射规律与修正前一致, 最高值出现在4月, 但月平均只有200 W/m², 降低了26 W/m², 降幅达到12%; 最低值出现月份有所改变, 出现在12月, 降幅为全年最高达到14%。年平均太阳辐射降低了15 W/m², 降幅为9%。

表 5

表 5 二滩水库库区太阳辐射月变化 Table 5 Monthly variation on solar radiation in Ertan reservior

表 5 二滩水库库区太阳辐射月变化 Table 5 Monthly variation on solar radiation in Ertan reservior

为了研究山区河流河岸坡度对月平均太阳辐射的影响, 再选取了20°,40°,50°坡度进行计算, 计算结果见表 6。研究发现, 不同坡度下库区水面可能的太阳辐射变化很大, 主要是由于太阳赤纬、地理纬度与河岸坡向坡度综合所致。就20°与50°两个坡度而言, 年平均值降低了56 W/m², 降幅高达34%, 最大降幅出现在11月与12月, 平均降低了46%, 绝对值降低了60 W/m²。坡度改变引起的太阳辐射改变总体上呈现冬大夏小的规律。

表 6

表 6 二滩水库不同坡度下库区太阳辐射月变化 Table 6 Monthly variation on solar radiation in Ertan reservior under different gradient

表 6 二滩水库不同坡度下库区太阳辐射月变化 Table 6 Monthly variation on solar radiation in Ertan reservior under different gradient

本文讨论了山区月平均气温和山区平行山脊太阳辐射的推算方法, 并以西南大型深水库---二滩水库为例说明了推算结果, 分析表明:

1) 将山区气温分解为经度、纬度、海拔高度和大地形影响4个订正项, 并采用多元线性回归方程进行拟合, 效果显著。利用同时期库区内盐边气象站的资料进行检验, 检验精度在0.5℃以内。

2) 利用山区平行山脊的太阳辐射计算方法, 对二滩水库库区太阳辐射进行计算和对比。结果显示, 与平地相比, 在山区地形遮蔽的影响下太阳辐射量有一定程度的改变。比较不同河岸坡度下水库水面接收的太阳辐射月平均值, 随着坡度的增大, 太阳辐射有较大改变。由于缺乏相关检验资料, 山地太阳辐射模型有待进一步修正与检验。