2. 北京市气象局气象信息中心, 北京 100089;
3. 中国科学院寒区旱区环境与工程研究所, 兰州 730000
2. Meteorological Information Center of Beijng, Beijng Meteorological Bureau, Beijing 100089;
3. Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000
相对于传统的通量观测仪器, 如涡动相关仪和波文比系统, 大孔径闪烁仪 (large aperture scintillometer, LAS) 最大的特点就是能测量500 m~10 km (超大孔径闪烁仪可达30 km) 范围的地表通量。在经过了20世纪70年代的繁盛期, 80年代的稳固发展期以及90年代初的衰退期之后, 国际上对大孔径闪烁仪的观测和研究又开始重视, 并在世界不同地区、不同下垫面开展了多次实验, 如WINTEX (Northern hemisphere climate Processes landsurface Experiment-Winter, 1997) [1], CASES-99 (Co-operative Atmosphere Surface-Exchange-Study 1999) [2], LITFASS (Lindenberg Inhomogeneous Terrain-Fluxes between Atmosphere and Surface : A Long-term Study, 1998, 2003) 等, 相关研究结果也已被总结[3-6]。
国内应用LAS的相关观测实验比较少。2000年中荷合作项目“中国能量与水平衡监测系统” (CEWBM S), 首次引进5套由荷兰瓦赫宁根大学研制的LAS设备, 分别安装在四川乐至、甘肃民勤、吉林乾安、湖南桃江和河南郑州5个地点, 开展了较长时间序列的水热通量观测, 但目前仅见有乐至、乾安和郑州站的数据使用[7-9]。2005年中荷合作项目“基于卫星的黄河流域水监测与河流预报系统”又在黄河河源区青海兴海、玛沁和唐克3处建立了LAS观测站[10]。北京师范大学等单位分别于2002年、2004年在北京昌平小汤山开展了LAS短期观测实验。此后, 借助全球环境基金 (GEF) “海河流域水资源与水环境综合管理项目”, 于2006年6月在北京密云新城子镇建立了LAS长期观测站, 至今已经积累了近两年的LAS观测数据。2007年8月, 又在河北馆陶建立起另一个LAS长期观测站。此外, 北京大兴的LAS观测站也于2008年5月建成。
LAS由发射仪和接收仪组成, 发射仪发出一定波长和直径的波束, 在大气中传播。接收仪接收受到光程路径上温度、湿度和气压波动影响的光, 并用折射指数结构参数 (Cn2) 来表征大气的湍流强度, 进而根据相似理论, 辅以气象数据计算出显热通量。由于LAS的测量尺度可与地表通量遥感估算模型或陆面过程模型、水文模型等像元或网格尺度相匹配, 因此成为模型验证的最佳地面通量观测仪器。已有的研究中, 主要包括3个方面: LAS的可用性研究, LAS观测中的相关问题研究以及LAS的应用研究, 如将不同下垫面上LAS观测的显热通量与涡动相关仪测值进行比较[3-4, 11], LAS观测过程中的饱和效应、掺混高度对LAS测值的影响, 利用两台不同波长的闪烁仪同时进行显热和潜热的观测等[3-5]。Beyrich等[12]和Jia等[13]将LAS测值用于数值天气预报模式 (NWP) 和蒸散量遥感估算模型 (SEBS) 的地面验证中。Hoedjes等[14]则进一步引入足迹的概念, 研究了LAS和涡动相关仪观测显热通量的尺度效应。
本文根据小汤山2002, 2004年以及密云2007年的LAS观测数据, 对影响LAS观测的显热通量 (HLAS) 的敏感因子进行分析, 探讨大气稳定条件下LAS的计算方法, 以及HLAS与对应时刻涡动相关仪测量结果 (HEC) 的比较。
1 观测实验与数据处理 1.1 观测实验本研究使用的大孔径闪烁仪观测数据, 分别为2002年和2004年北京昌平小汤山国家精准农业研究示范基地以及2007年北京密云观测站的资料。
2002年小汤山 (40°10′41″N, 116°26′52″E) 实验从3月26日至8月18日 (4月23日以后仅有LAS的观测), 实验场是平坦裸地, 东西宽450 m, 南北长1000 m。在实验场的西北和东北角各放置1台LAS发射仪, 接收仪在实验场南端 (光径长度934 m, 架高4 m, LAS150, 荷兰瓦赫宁根大学)。在实验场的中间位置有一套涡动相关仪 (架高2 m, 超声风速仪: DA600, KAIJO, 日本; CO2/H2O分析仪: Li7500, Campbell) 测量地表水热通量, 并有净辐射等观测。2004年在同一实验场开展了LAS观测实验, 设在实验场中间的道路将其分成南北两个小区, 下垫面分别为裸地和杂草地。在南北小区的中间位置设立了两个观测点, 各有1套涡动相关仪 (南北架高分别为1.8 m和1.9 m, 超声风速仪: CSAT3, Campbell; CO2/H2O分析仪:Li7500, Campbell) 和自动气象站进行地表通量和气象要素观测, 同时辅以净辐射等观测。在实验场南端和北端铁塔上分别架设LAS的发射仪和接收仪 (光径长度1000 m, 架高8 m, LAS150, 荷兰瓦赫宁根大学)。
密云观测站 (40°37′50.8″N, 117°19′23.8″E) 位于宽度约500~1000 m, 长度约2400 m的西南-东北走向山谷中, 下垫面以果树林、耕地和居民地为主。一套LAS (Kipp & Zonen, 荷兰) 装置在南北两座小山顶, 光程2420 m, 有效高度35.86 m, 西南面为接收端。在LAS光径路径中间、距离接收端900 m处, 一套涡动相关仪 (超声风速仪: CSAT3, Campbell; CO2/ H2O分析仪: Li7500, Campbell) 架设在一铁塔上, 架高26.66 m, 在该塔上还有净辐射、降水量、气压以及两层 (10.66 m, 30.56 m) 的风、温、湿等气象要素观测。该实验场从2006年8月正式运行以来, 已积累了两年多的数据。
1.2 数据处理在2002年和2004年小汤山实验中, LAS每4 s采集1次数据, 后期处理为10 min数据集; 密云站的LAS每2 s采集1次数据, 后期处理为30 min数据集。在数据处理中, 对空气折射指数结构参数Cn2的饱和效应进行了检查。所谓Cn2的饱和效应, 指当闪烁强度达到一定上限时, 关系式Cn2=1.12σlnI2D7/3LLAS-3不再成立 (其中σlnI2为接收到的光强自然对数的方差, D为光学孔径, LLAS为发射仪与接收仪之间的距离), 即发生饱和。Ochs等[15]给出的Cn2饱和上限为0.193LLAS-8/3λ2/6D5/3, 其中λ是发射波长。由此得到2002年、2004年小汤山和2006年后密云实验的Cn2饱和上限分别为9.4×10-13, 8.0×10-13和9.6×10-14。
根据研究的需要, 利用以下标准对前面两次短期观测实验的LAS观测数据进行筛选: ①仅用白天不稳定层结时段的数据; ②非降雨天; ③对应时刻涡动相关仪工作正常。由此得到2002年、2004年小汤山的合格样本数分别为:752(3月30日-4月21日)、718(5月30日-6月15日)。
对于密云观测站, 本研究计算了2007年全年的LAS观测显热通量HLAS。计算中删除Cn2饱和时的数据、降水时次和该时次前后1 h的数据以及对应时刻没有涡动相关仪测量的数据。HLAS计算中需要的气象数据来自同一观测实验中涡动相关仪以及自动气象站梯度的观测。其中涡动相关仪的观测数据采用EdiRe软件进行了后期处理[16], 但2002年除外 (未存储原始湍流资料, 直接使用仪器自带软件输出的通量值)
敏感性分析使用2004年小汤山的数据; 稳定条件下HLAS的计算使用2007年密云站的数据; HLAS与HEC的比较使用了小汤山 (2002, 2004年) 和2007年密云站的数据。
2 敏感性分析在LAS显热通量的计算过程中, 首先由观测的空气折射指数结构参数Cn2计算温度结构参数CT2, 然后根据莫宁-奥布霍夫近地层相似理论, 按Panofsky等[17]给出的CT2和显热通量之间的关系式, 辅以气象参数 (风速u、空气温度T、气压p) 迭代求解HLAS。主要公式如下:
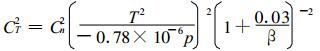
|
(1) |
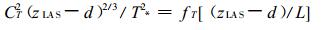
|
(2) |
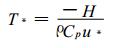
|
(3) |
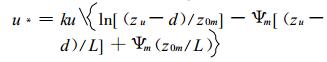
|
(4) |
其中, zLAS为闪烁仪光径高度; zu为风速的观测高度; d为零平面位移; ρ为空气密度; β为波文比; Cp为空气定压比热; H为显热通量; L为莫宁-奥布霍夫长度; k为卡曼常数; z0m为动力学粗糙度; T*为摩擦温度; u*为摩擦速度, Ψm为动量稳定度修正函数, fT为稳定度普适函数。本文利用2004年小汤山的LAS观测数据 (718个样本), 讨论波文比β、气象参数u, T以及下垫面参数d, z0m及光径高度zLAS对LAS观测显热通量的影响。
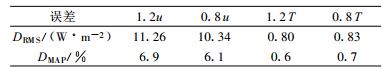
2.1 波文比β的影响在式 (1) 中, 波文比是一个表征大气湿度影响的修正项。波文比越大, 对CT2的影响越小, 反之影响越大。前人研究中, 波文比的取值一般有两种情况:忽略波文比修正项[18], 或者根据地表干湿状况, 对波文比赋予一定值[19-20]。2004年小汤山实验期间, 波文比变化范围为0.23~2.85, 以此计算的显热通量为参考值, 讨论如下4种波文比取值对HLAS的影响: ①β=0.3(湿润); ②β=0.65(正常); ③β=1(干旱); ④β→∞(不考虑波文比)。表 1是4种条件下得到的显热通量与参考值比较的均方根误差DRMS和平均绝对百分比误差DMAP。
|
|
表 1 波文比不同取值条件下得到的显热通量HLAS与参考值的比较 Table 1 Statistics of HLAS flux estimated with different β against the reference value |
从表 1可见, 当β从0.3变化到1.0过程中, DRMS和DMAP均减小。这是由于观测站点属于温带半干旱区域, 波文比在观测期间大部分时候大于0.3。β=0.3属于湿润情况, 低估显热通量约8 %。当波文比取一个恰当值 (0.65或1.0) 时, 得到的显热通量与参考值的差异很小, DRMS和DMAP分别约为3~4W·m-2和2%~3%。若不考虑波文比, DRMS和DMAP分别增大为6.51W·m-2和5.3%, 但仍小于β=0.3的情况。这与前人的研究结果一致。DeWekker[21]指出, 当β>0.6, 波文比修正项可以不考虑。因此, 在干旱、半干旱地区, 波文比可以忽略或者赋予一个定值, 简化计算而对结果影响不大。但若地表湿润, 则需要准确确定波文比。
2.2 气象参数u, T的影响HLAS计算需要3个气象参数:气压p、风速u和空气温度T。其中, 气压p一般变化不大; 对于风速u和空气温度T, 在其他条件不变情况下, 分别浮动±20%计算显热通量, 并与参考值比较 (表 2)。气温变化±20%对计算HLAS的影响非常小, DRMS仅0.8W·m-2左右。而对于风速变化±20%则会高估 (低估) 显热通量8%左右, DRMS可达11W·m-2。一般风速和空气温度的观测误差分别为0.5m·s-1和0.5℃。观测期间二者的平均值分别为2.7m·s-1和29.0℃, 传感器可能引起的观测误差约为18.5%和1.7%。因此气温的观测误差基本不会对显热通量的计算产生影响, 而风速的取值需要准确确定。
|
|
表 2 风速u和空气温度T不同取值条件下得到的显热通量HLAS与参考值的比较 Table 2 Statistics of HLAS estimated under different conditions of u and T against the reference value |
2.3 零平面位移d、动力学粗糙度z0m及有效光径高度zLAS的影响
式 (2)~(4) 表明, 零平面位移d和动力学粗糙度z0m以及闪烁仪光径有效高度zLAS是计算显热通量的关键因子。小汤山实验场由南北两块面积近似相等但下垫面不同 (裸地、杂草地) 的区域组成, 光程路径上的d和z0m可由南北区域的组分值按照面积权重比求和得到: d=0.0867 m, z0m=0.0114 m (5月30日-6月11日) 和0.0205 m (6月12-15日) [22-23]。根据Verhoef等[24]的研究结果, 将d和z0m浮动±50%后计算显热通量, 并与参考值比较。对于光径高度zLAS, 在小汤山平坦地表, 即为仪器架设高度, 但在非平坦地表, 式 (2) 中需要的是有效光径高度。本研究中将zLAS浮动±20%后与显热通量参考值比较 (表 3)
|
|
表 3 d, z0m和zLAS不同取值条件下得到的显热通量HLAS与参考值的比较 Table 3 Statistics of HLAS estimated under different conditions of d, z0m and zLAS against the reference value |
2004年小汤山实验场是裸地与杂草地的混合下垫面, 当d在估算误差范围内变化, 对计算的显热通量影响很小。这是由于与光径高度 (8 m) 相比, d很小。从式 (2) 可见, 在这种情况下, d可以忽略。但当地表粗糙元的高度变化相对于光径高度zLAS不可忽略时, d需要精确确定[18]。当z0m在误差范围内变化时, 对应的DRMS和DMAP分别在4~7W·m -2和2%~4%。也就是说, z0m的估算误差对LAS观测的显热通量值影响不大, 即HLAS对z0m不敏感。而光径高度zLAS浮动±20%时, 得到的DRMS和DMAP比d, z0m大1~2个数量级。因此, 非平坦地表有效zLAS值需要精确计算。
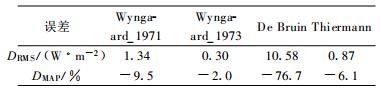
3 稳定条件下显热通量HLAS的计算 3.1 稳定条件下普适函数fT的选择目前夜间稳定条件下HLAS的研究很少。这主要是由于在夜间稳定条件下, 尤其是风速很小、大气非常稳定时, 相似关系有很大的不确定性。密云观测站地处谷地中, 夜间风速一般较小 (0~2 m·s-1), 计算中迭代过程常不收敛。根据大气近地层相似理论, 临界理查孙数Ri≈0.2时, 相似关系不再适用。为简单起见, 设定式 (4) 中Ψm的下限值为-5。到目前为止, Andreas, Wyngaard (1971, 1973) 等, Thiermann等, De Bruin等均给出过计算HLAS的稳定性普适函数[25], 其中不稳定条件下各表达式相互接近, 稳定条件下各研究者提出的fT函数却有较大的不同。密云站的LAS仪器由Kipp & Zonen (荷兰) 公司生产, 本文用其说明书中推荐的Andreas的函数作为稳定条件下的普适函数fT_Andreas。该函数由fT_Wyngaard 1971和fT_Wyngaard 1973函数得来, 与Thiermann等给出的差异不大。分析中用2007年4月稳定条件下的数据 (829个样本), 以fT Andreas函数的计算值为参考值, 与其他函数的计算结果做比较 (表 4)。除了fT_De Bruin函数, 其他3个函数与fT_Andreas函数的计算值非常接近, DRMS在1 W·m-2左右, 最大的DMAP不超过10%。而fT_De Bruin函数在稳定条件下等于常数, 与f T_A ndreas函数得到的HLAS的差异很大 (DMAP=-76.7%), 但因HLAS量值较小, DRMS仍较小。因此, 本文所选的fT_Andreas函数具有代表性。
|
|
表 4 稳定条件下不同普适函数与fT_Andreas函数得到的HLAS值之间的比较 Table 4 Statistics of HLAS estimated with different fT_functions against the one with fT_Andreas under stable condition |
3.2 大气稳定度的判断
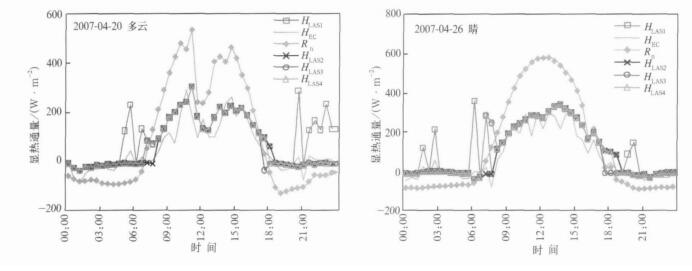
LAS仅能观测到大气湍流的强度, 但是不能判断湍流引起的标量输送方向, 即通量的符号。本研究中, 首先利用密云站涡动相关仪测量的HEC来判断大气稳定状况[18], 即取HLAS与HEC同号 (HLAS1表示)。以2007年4月20日和26日为例 (图 1), HEC和HLAS1在白天不稳定情况下是可比的, 但对夜间以及早晚稳定度转换时刻, 当HEC为很小的正值时, 对应的HLAS1为很大的正值, 与常理不符。其原因一方面是夜间偏稳定情况下HEC的测量误差相对较大, 另一方面也与涡动相关仪和LAS观测的通量源区范围差异较大有关 (在不同尺度上测量通量的符号可能不同)。再利用密云站气象梯度观测计算的理查孙数Ri确定HLAS的符号 (HLAS2), 与前者比较, 夜间或早晚稳定度转换时刻HLAS出现的很大正值消失了, HLAS与HEC日变化趋势的吻合程度明显改善。据此, 计算了该站2007年的HLAS值。
|
|
| 图 1. 利用HEC(HLAS1)、梯度理查孙数Ri(HLAS2)、日出日落时间 (HLAS3) 和净辐射 (HLAS4) 确定HLAS符号得到的HLAS与HEC以及净辐射Rn的比较 Fig 1. Daily variation of HLAS, HEC and Rn with the sign of HLAS determined by the measured HEC(HLAS1), Richardson number (HLAS2), sunrise-sunset time (HLAS3) and net radiation (HLAS4) | |
没有梯度观测的站, 可根据日出日落时间判断大气的稳定度 (日出后2 h至日落前2 h为大气不稳定, HLAS3) [12], 也可根据净辐射测值来判断 (Rn > 10W·m-2为白天不稳定状态, HLAS4) [5]。图 1中, 日出日落时间法与理查孙数法判断的稳定度转折时刻大约相差0.5~2 h, 且早晚的转折时刻, 前者均早于后者。对于净辐射法, 在早上转折时刻比理查孙数法早进入不稳定状态, 在晚上转折时刻与理查孙数法判断的稳定度状况比较一致, 好于日出日落时间法。在稳定度转换过程中, HLAS值由正 (负) 到负 (正) 是一个渐变的过程, 理查孙数法能较好地反映这个变化过程, 而日出日落时间法和净辐射法有些偏差。这两种方法计算的日HLAS与理查孙数法计算值的偏差分别为9%, 6%(4月20日) 和16.7%, 12.4% (4月26日)。以上比较表明:利用日出日落时间和净辐射也可用于HLAS计算中稳定度的判断。
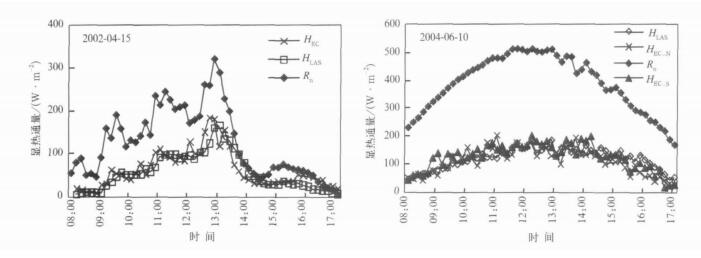
4 显热通量HLAS的日变化和月变化 4.1 不同下垫面上显热通量的日变化选取2002年小汤山 (均匀裸地下垫面) 和2004年小汤山 (一半裸地和一半杂草地组成的非均匀下垫面) 各1个典型天为例 (图 2), 在均匀、非均匀的下垫面上, HLAS和HEC的日变化曲线都与净辐射日变化曲线趋势一致。净辐射的波动能迅速反映到测量的HLAS和HEC值上, 反映其为地气间能量交换的驱动因子。在均匀地表, 由于两个仪器均测量的是裸地上的通量值, HLAS和HEC的变化范围很接近。在非均匀地表, HLAS的曲线比HEC曲线平滑, 且基本介于南北两个涡动相关仪测值之间。这是由于LAS测量的是整个非均匀地表上的平均状况, 而架设在南北区域中间位置的涡动相关仪则分别测量裸地和杂草地的显热通量。这两个短期实验的观测表明, LAS在均匀、非均匀地表, 都能得到比较合理的测量结果。这与前人的研究结果一致[3-4, 11-12]。
|
|
| 图 2. 均匀、非均匀地表上HLAS, HEC与净辐射Rn在白天的变化 Fig 2. Daily variation of HLAS, HEC and Rn over homogeneous, heterogeneous surfaces | |
4.2 显热通量HLAS的月变化
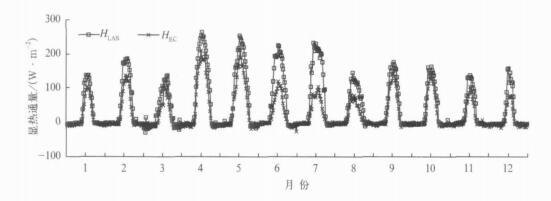
对1个月内每天对应时刻HLAS和HEC有效值取平均, 可以得到代表该月的平均日变化情况。图 3是2007年密云站HLAS与HEC的月变化。白天的HLAS值大于HEC, 夜间两者很接近且绝对值都小, 随时间几乎无变化。其中3月的HLAS和HEC曲线较其他月份波动大, 这是由于仪器标定仅用12 d的数据得到月平均, 样本数较少的缘故。
|
|
| 图 3. 2007年密云站HLAS与HEC的月变化 Fig 3. Monthly variation of HLAS and HEC in 2007 of Miyun | |
1-3月, HLAS的变化范围都在200 W·m-2以下; 4-5月可超过250W·m-2。其中3-4月, 显热通量突然增加。这是由于进入春季以后, 太阳开始直射北半球, 净辐射明显增加 (3, 4月的平均Rn分别为52.0W·m-2, 94.8W·m -2), 而此时地表植被尚处于发芽 (园地) 或播种 (耕地) 阶段, 潜热通量小。6-7月是植被生长季节, 蒸腾强烈, 净辐射有较大部分转化为潜热通量 (6, 7月平均Rn和潜热通量分别为120.2W·m-2, 59.1W·m-2和141.2W·m-2, 73.5W·m-2), HLAS的最大值又有所回落 (200~250W·m-2)。8月HLA S峰值回落至150W·m-2左右, 此时潜热通量较大 (8月平均Rn和潜热通量分别为135.8W·m-2和74.4W·m-2)。9-12月, HLAS峰值保持在150W·m-2左右。根据通量贡献源区的分析[26], 涡动相关仪和LAS观测的显热通量的差异随季节而变化, 主要在于两个仪器通量贡献源区的大小差异。对于涡动相关仪, 通量贡献源区绝大部分来自果树林, 显热通量较小 (特别在夏季); 而LAS的通量贡献源区除果树林外, 还有耕地及居民地, 显热通量较大。
5 结论与讨论本研究的敏感性分析表明, 对于HLAS的计算, 在干旱、半干旱地区, 波文比可以不考虑或者赋予一个定值。但对湿润地表, 则需要预先确定波文比值。风速的观测误差会对显热通量的计算精度带来较明显的影响, 但气温的观测误差影响很小。HLAS的计算对LAS光径高度zLAS较敏感, 尤其是非平坦地表, 需要精确确定。对于零平面位移d, 若zLAS远大于d, 则d可以忽略或简单取值; 反之d为敏感因子。而空气动力学粗糙度z0m则是一个不敏感参数。
稳定条件下HLAS的计算主要有两个困难:一是稳定度普适函数目前尚无统一的表达式, 本文采用仪器说明书中推荐的函数; 二是大气稳定度的确定问题, 本研究根据理查孙数Ri判定大气稳定度, 得到较好的日变化结果。在没有梯度测量条件下, 也可根据日出日落时间和净辐射判定大气稳定度。需要指出的是, 稳定条件下HLAS的计算, 还存在很多问题, 尤其是稳定度函数的选择, 相似理论的可用性等等, 本文仅作了初步的研究。同时, 利用日出日落时间和净辐射确定HLAS符号的普适性, 也需要进一步的验证。
从本研究中几个站点测量的HLAS可以看出, LAS在均匀和非均匀地表上都可以得到合理的测量值。其与涡动相关仪测量值的差异, 需要结合涡动相关仪和LAS的通量贡献源区以及涡动相关仪的能量闭合程度, 做进一步的分析研究。
| [1] | De Bruin H A R, Meijninger W M L, Smedman A-S, et al. Displaced-beam small aperture seintillometer test. Part Ⅰ: The WINTEX data-set. Boundary-Layer Meteorol, 2002, 105: 129–148. DOI:10.1023/A:1019639631711 |
| [2] | Hartogensis O K, De Bruin H A R, Van De Wiel B J H, Displaced-beam small aperture scintillometer test. Part Ⅱ: CASES-99 stable boundary-layer experiment. Boundary-Layer Meteorol, 2002, 105: 149–176. DOI:10.1023/A:1019620515781 |
| [3] | Meijninger W M L, Hartogensis O K, Kohsiek W, Determination of area-averaged sensible heat fluxes with a large aper ture seintillomeler over a heterogeneous surface-Flevoland field experiment. Boundary-Layer Meteorol, 2002, 105: 37–62. DOI:10.1023/A:1019647732027 |
| [4] | Meijninger W M L, Green A E, Hartogensis O K, et al. De termination of area averaged water vapor fluxes with large aperture and radio wave seintillometers over a heterogeneous surface-Flevoland Field Experiment. Boundary-Layer Meteorol, 2002, 105: 63–83. DOI:10.1023/A:1019683616097 |
| [5] | Kohsiek W, Meijninger W M L, De Bruin H A R, et al. Saturation of the large aperture scintillometer. Boundary-Layer Meteorol, 2006, 121: 111–126. DOI:10.1007/s10546-005-9031-7 |
| [6] | 卢俐, 刘绍民, 孙敏章, 等. 大孔径闪烁仪研究区域地表通量的进展. 地球科学进展, 2005, 20, (9): 932–938. |
| [7] | 胡丽琴, 吴蓉璋, 方宗义. 大口径闪烁仪及其在地表能量平衡监测中的应用. 应用气象学报, 2003, 14, (2): 197–205. |
| [8] | Min W, Chen Z, Sun L, et al. A scheme for pixel-scale aerodynamic surface temperature over hilly land. Adv Atmos Sci, 2004, 21, (1): 125–131. DOI:10.1007/BF02915686 |
| [9] | 支克广, 涂钢, 廉毅, 等. 乾安地区盐碱地显热通量的测量. 气象学报, 2002, 60, (6): 780–785. |
| [10] | 杜得彦. LAS原理及其在黄河河源区的应用. 水文, 2007, 27, (2): 71–73. |
| [11] | McAneney K J, Green A E, Astill M S, Large aperture scintillometry: The homogeneous case. Agric For Meteorol, 1995, 76: 149–162. DOI:10.1016/0168-1923(95)02227-O |
| [12] | Beyrich F, De Bruin H A R, Meijninger W M L, et al. Resuits from one-year continuous operation of a large aperture scintillometer over a heterogeneous land surface. Boundary-Layer Meteorol, 2002, 105: 85–97. DOI:10.1023/A:1019640014027 |
| [13] | Jia L, Su Z, Van Den Hurk B, et al. Estimation of sensible heat flux using the Surface Energy Balance System (SEBS) and ATSR measurements. Phys Chem Earth, 2003, 28: 75–88. DOI:10.1016/S1474-7065(03)00009-3 |
| [14] | Hoedjes J C B, Chehbouni A, Ezzahar J, et al. Comparison of large aperture seintillometer and eddy eovarianee measure ments: Can thermal infrared data be used to capture footprint-induced differences?. J Hydrometeorol, 2007, 8: 144–159. DOI:10.1175/JHM561.1 |
| [15] | Ochs G R, Wilson J J. A Second-generation Large Aperture Scintillometer. NOAA Tech Memor, ERL ETL-232, NOAA Environmental Research Laboratories, Boulder, CO, USA, 1993. |
| [16] | 徐自为, 刘绍民, 宫丽娟, 等. 涡动相关仪观测数据的处理与质量评价研究. 地球科学进展, 2008, 23, (4): 357–370. |
| [17] | Panofsky H A, Dutton J A, Atmospheric Turbulence: Model and Methods for Engineering Applications. New York: Wiley, 1984. |
| [18] | Cain J D, Rosier P T W, Meijninger W, et al. Spatially aver aged sensible heat fluxes measured over barley. Agric For Meteorol, 2001, 107: 307–322. DOI:10.1016/S0168-1923(01)00214-3 |
| [19] | Meijninger W M L, De Bruin H A R, The sensible heat fluxes over irrigated areas in western Turkey determined with a large aperture scintillometer. J Hydrol, 2000, 229: 42–49. DOI:10.1016/S0022-1694(99)00197-3 |
| [20] | Hemakumara H M, Chandrapala L, Moene A F, Evapotranspiration fluxes over mixed vegetation areas measured from large aperture scintillometer. Agric Water Man, 2003, 58: 109–122. DOI:10.1016/S0378-3774(02)00131-2 |
| [21] | De Wekker S F J. The Estimation of Areally-averaged Sensible Heat Fluxes over Complex Terrain with a Large-aperture Seintillometer. Department of Meteorology, Wageningen Agricultural University, 1996. |
| [22] | Lagoarde J P, Bonnefond J M, Kerr Y H, et al. Integrated sensible heat flux measurements of a two-surface composite landscape using scintillomtetry. Boundary-Layer Meteorol, 2002, 105: 5–35. DOI:10.1023/A:1019631428921 |
| [23] | Taylor P A, Comments and further analysis on effective roughness lengths for use in numerical three-dimensional models. Boundary-Layer Meteorol, 1987, 39: 403–418. DOI:10.1007/BF00125144 |
| [24] | Verhoef A, De Bruin H A R, Van Den Hurk B, Some practical notes on the parameter kB-1 for sparse vegetation. J Appl Meteorol, 1997, 36: 560–572. DOI:10.1175/1520-0450(1997)036<0560:SPNOTP>2.0.CO;2 |
| [25] | 卢俐.地表显热通量的观测、影响因子和尺度关系的研究.北京:北京师范大学, 2008. |
| [26] | 宫丽娟.地表通量观测的空间代表性研究.北京:北京师范大学, 2008. |
 2009, 20 (2): 171-178
2009, 20 (2): 171-178