应用气象学报  2009, 20 (2): 164-170   PDF    
引用本文
陈峰峰, 王光辉, 沈学顺, 陈德辉, 胡江林. Cascade插值方法在GRAPES模式中的应用[J]. 应用气象学报, 2009, 20(2): 164-170.
Chen Fengfeng, Wang Guanghui, Shen Xueshun, Chen Dehui, Hu Jianglin. Application of Cascade Interpolation to GRAPES Model[J]. Journal of Applied Meteorological Science, 2009, 20(2): 164-170  
Cascade插值方法在GRAPES模式中的应用
陈峰峰, 王光辉, 沈学顺, 陈德辉, 胡江林     
中国气象科学研究院灾害天气国家重点实验室, 北京 100081
2008-01-31 收到, 2008-12-16 收到修改稿.
资助项目: 国家自然科学基金项目 (40675063, 40745033, 40675062)、“十一五”国家科技支撑项目“灾害天气精细数值预报及短期气候集合预测研究”共同资助    
摘要: 基于半拉格朗日 (semi-Lagrangian) 方案的数值天气预报模式, 求解半拉格朗日轨迹上游点变量, 通常采用传统直线逐点拉格朗日多项式插值, 由已知模式格点 (欧拉网格点) 的数值插值获得。对于三维空间上游点的插值, N阶精度需要O(N3) 运算量。N增大, 运算量将大幅增加, 特别耗费计算机机时, 而采用Cascade插值法 (降阶插值法) 则只需要O(N) 运算量。它的显著特点是:用曲线代替直线, 通过一系列中间过渡网格点, 在曲线上用一维拉格朗日插值, 使得相邻拉格朗日格点或中间过渡点的插值不再是孤立的, 而且可以重复使用某些中间结果, 达到减少运算量的目的。将这种方法合理应用于GRAPES模式, 并根据模式的特点, 对Cascade插值过程中独立变量的距离分段计算, 从而有利于实现并行计算。计算结果表明Cascade插值法与传统直线逐点插值法相比, 计算效率平均提高约30%, 同时不降低精度。
关键词: 欧拉网格点    拉格朗日网格点    Cascade插值方法    GRAPES模式    
Application of Cascade Interpolation to GRAPES Model
Chen Fengfeng, Wang Guanghui, Shen Xueshun, Chen Dehui, Hu Jianglin     
State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
Abstract: For the numerical weather predicting model (NWM) based on semi-Lagrange scheme, it is not economical to apply the conventional point-by-point approach based on Cartesian product of one-dimensional Lagrange interpolation polynomials to evaluate up-stream variables at each integration time step. It takes O(N3) operations to calculate each point. The bigger the N value is, the more accurate the calculation may become. However, it involves too much calculation. When the method of a Cascade of one-dimensional interpolation of the entire data is employed, it requires only O(N) operations. The so-called Cascade method is a highly efficient means of carrying out the grid-to-grid interpolations required by a high-order semi-Lagrangian model. It goes like follows: The intersection points between the regular Eularian and curvilinear Lagrangian meshes form hybrid coordinate lines, and some variables of the intermediate points and the target point of the Lagrangian mesh can be interpolated by using one-dimensional curvilinear Lagrange interpolation method. First, the values of all intermediate points are interpolated. Then, the values of the target points are interpolated from the evaluated intermediate values step by step.The interpolation of the target points is not isolated because the adjoining target point uses shared some intermediate points. Some intermediate results can be repeatedly utilized so that it reduces the amount of computation in interpolation process. GRAPES (Global/Regional Assimilation and Prediction System) is a new generation of numerical weather prediction system of China developed by Research Center for Numerical Meteorological Prediction of CAMS (Chinese Academy of Meteorological Sciences) of CMA (China Meteorological Administration). It is designed based on the scheme using two time-level semi-Implicit time integration and semi-Lagrangian backward trajectories. It is also a fully compressible, non-hydrostatic grid model using latitude and longitude, as well as terrain-following height vertical coordinate. The model variables are staggered in two-dimension horizontal space in the form of an Arakawa-C grid. According to the designing principles of softw are engineering, GRAPES is a standardized, modularized, and coding infrastructure system. As far as the big numerical predicting models are concerned, the parallel computing becomes a necessary feature of them. The parallel computation of GRAPES is realized by means of decomposing zone in latitude and longitude directions. In order to parallelize Cascade interpolation code conveniently, the independent variables like distance on the curves need to be calculated in individual subsections instead of those from the start point. When the Cascade interpolation is applied in GRAPES model, predicting models are tested based on different horizontal grid resolutions such as those of 50km (720×360) and 100km (360×180). There are 31 vertical levels altogether.The timing of interpolating upstream points is monitored on the IBM-1600 cluster in CMA.The results of tests show that Cascade interpolation can significantly reduce computer running time by about 30%, compared with the conventional Cartesian interpolation, without affecting the accuracy of predicting models.
Key words: Euler meshes     Lagrange meshes     Cascade interpolation     GRAPES mode    
引言

数值天气预报模式积分中长期存在的问题之一是稳定性制约最大时间步长的选择, 而不是精度[1]。为了模式积分稳定, 选择小时间步长以便使时间截断误差比空间截断误差小许多, 这样势必要求更多的时间步数, 因此选择时间积分方案在设计模式中至关重要。数值天气预报中的一个重要发展是半拉格朗日技术[1-5], 此方法的显著特点是:时间积分步长选择打破了传统CFL (Courant-Friedrich-Lewy) 稳定性准则的限制, 允许选择较长的时间步长, 从而提高计算效率[4, 6-8]。已证明半拉格朗日方案对于有效积分控制方程是一种好选择[2]。随着拉格朗日技术在数值天气预报中的应用, 半拉格朗日平流方案最近几年逐渐成为一种趋势, 并已在ECMWF, UKMO, 法国气象局, CMC等的静力或非静力模式中得到广泛应用[9-11]。

GRAPES[12-14] (Global/ Regional Assimilation and PrEdiction System) 系统是在中国气象局与国家科技部共同支持下, 由中国气象科学研究院数值预报中心承担, 会同高校、研究院、所等部门的专家协同完成的新一代全球/区域同化预报系统。GRAPES模式是一个格点模式, 它的动力框架使用一套完全非静力、全可压的方程组, 积分方案使用两时间层的半隐式半拉格朗日时间差分方案[14]。拉格朗日轨迹是向后的轨迹, 拉格朗日轨迹上游点为三维空间插值目标点, 是非模式网格点。这些上游点变量在每一个时间步长都要由已知周围模式格点“插值”计算, 即从已确定的规则欧拉网格点的数值插值到相应不规则拉格朗日网格点 (即由上游点位置定义的曲线网格点)。采用传统逐点拉格朗日多项式插值方法, 对于每一个拉格朗日格点插值需要进行O(N3) 运算 (N代表插值精度的阶数, N=4为三次插值), 此方法易于实现, 但相当耗费机时, 特别是应用高阶插值。对此, Purser等提出一种简单而又比较经济的插值方法[4], 即Cascade插值法 (降阶-插值法), 后来经过Nair等[7]进一步对其进行改进与完善。Cascade插值法计算每个点只进行O(N) 运算[7]。在半拉格朗日技术的应用过程中, 传统的方法是基于一维拉格朗日插值多项式的笛卡尔 (Cartesian) 乘积; 而Cascade插值则是通过混合网格作一连串一维插值, 这种混合网格是标准的欧拉坐标和曲线拉格朗日坐标的混合体。另外Cascade也可应用于向前轨迹, 由不规则网格到规则网格插值[15]。对于GRAPES这样大型数值预报模式程序而言, 并行计算是其必需采用的技术手段[16], 应用Cascade插值法, 曲线上一维拉格朗日插值, 距离为变量, 从曲线上各点以起始点的距离计算变为相对于某点距离计算, 使其利于在并行模式中应用。

1 插值简介 1.1 传统直线拉格朗日插值

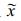
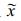
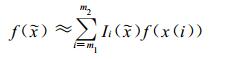
若已知一维区间[a, b]中n个互不相同的离散节点x (i) (i=1, 2, …n) 处的函数值为f (x(i)), 插值求解区间“目标”位置处的函数值f (), 用一维拉格朗日插值多项式表示为:

(1)
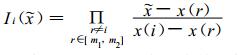
(2)

其中, Ii() 为P=m2-m1次插值基函数, N=m2-m1+1为插值所使用的离散节点个数, 称为插值阶数。一般选取插值节点跨越, 两边插值节点的个数尽量相同, 对每个插值目标点需要O(N) 运算量。

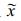
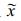
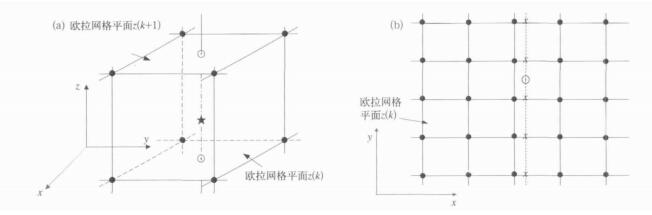
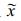
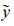
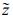
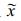
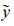
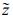
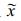
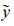
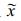
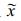
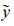
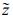
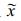
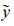
若已知欧拉三维网格坐标格点{x (i), y (j), z(k) }的函数值f(x(i), y(j), z (k)) (其中i=1, 2, …, m; j=1, 2, …, n; k=1, 2, …, p为格点序号), 求解三维目标点 (, , ) 的函数值f (, , )。其方法是:首先, 通过该点的直线与z=z (k) 的欧拉平面 (k固定, i, j变化的欧拉网格点组成的平面) 垂直相交, 交叉点为第一类中间过渡点, 其在欧拉平面z (k) 上, 坐标为 (, ); 然后, 在欧拉平面z (k) 上过第一类中间过渡点的直线与欧拉网格线y(j) (k, j固定, i变化的欧拉网格点构成的直线) 垂直相交, 交点为第二类中间过渡点 (如图 1所示), 其在y(j) 上的位置为 ()。在欧拉网格线上利用一维拉格朗日式 (1) 和式 (2) 插值第二类中间过渡点的函数值, 通过已求得的第二类中间过渡点插值求第一类中间过渡点函数值, 最后, 由第一类中间过渡点插值求 (, , ) 函数值f (, , )。其三维拉格朗日插值多项式可表示为:

图 1. 三维空间拉格朗日三次插值 (a) 三维空间单网格 (●为欧拉网格点; ★表示三维目标点; ⊙表示过★目标点直线与欧拉网格平面z(k) 垂直交叉点), (b) 二维空间水平网格 (x表示平面上过⊙直线与欧拉网格线y(j) 垂直交叉点; 计算⊙点和★点运算量分别为O(N2) 和O(N3), N=4为三次插值) Fig 1. The cubic interpolation schematics of a three-dimension space point using Cartesian product technique (a) schematic illustration of a single grid in three-dimension space (●Eularian grids points; ★ the three-dimension space target points; ⊙ intersection point between line and level panel through ★ point), (b) schematic illustration of a horizontal grids in two-dimension space (x the intersection points betw een the line through ⊙ point and Eularian grid lines y(j) on level panel; the computation operation of the ⊙ and ★ points is O(N2) and O(N3), respesctively, N=4 for cubics)

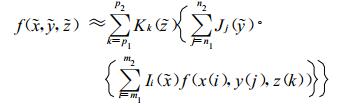
(3)

其中,

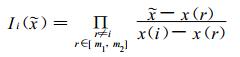
(4)
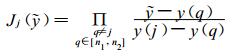
(5)
(6)

利用式 (3)~(6) 计算每一个上游点函数值, 是基于采用一维拉格朗日插值多项式的Cartesian乘积。实际应用插值次数取:

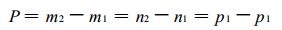
(7)

其运算大约为O(N3) 量级。用这种传统方法求解场中每一个拉格朗日上游点, 其各自孤立计算, 中间过渡点及拉格朗日格点的插值均互不相关, 一个上游点的中间过渡点的插值结果不能被其他点插值使用。

1.2 三维空间的Cascade插值

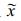
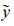
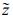
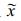
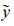
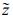
采用半拉格朗日的格点模式, 一个重要过程是由规则模式网格点的变量值插值计算拉格朗日轨迹上游点的变量值, 模式网格就是欧拉网格。对于每个欧拉网格点则对应一个拉格朗日上游点的位置。设欧拉网格点的坐标为{ x(i), y(j), z(k) } (i, j, k为欧拉网格序号), 分别将i, j, k中两个固定不变, 另一个变化的欧拉网格点所对应的上游点逐点连接构成拉格朗日曲线网格, 其网格点的坐标表示为{ (i, j, k), (i, j, k), (i, j, k) }。Cascade插值法就是利用欧拉网格与拉格朗日网格组成的混合网格, 在曲线上分步进行一维拉格朗日插值。通过重复使用一些中间插值过程的计算结果, 从而达到减少运算量的目的。方法是:对拉格朗日网格, 将i, j固定, k变化的点{ (i, j, k), (i, j, k), (i, j, k) }逐点用直线连接构成的曲线与欧拉网格的n层平面z=z(n) (n固定, i, j变化的欧拉网格点组成的平面) 相交, 交叉点为第一类中间过渡点, 其坐标表示为{x1(i, j, n), y1(i, j, n), z1 (i, j, n) }。为便于描述, 该曲线称为l1曲线; 在平面z(n) 上, i固定, j变化, 对形成的第一类中间过渡点逐点用直线连接构成曲线l2, 曲线l2与z(n) 平面上的欧拉网格线 (n层欧拉网格平面上序号为j欧拉网格线) 交叉获得第二类中间过渡点; 在欧拉网格线上应用一维拉格朗日多项式式 (1)、式 (2) 由已知欧拉网格变量值计算第二类中间过渡点的变量值; 在第一类中间过渡点和第二类中间过渡点所在的l2曲线上, 通过第二类中间过渡点应用一维插值, 获得第一类中间过渡点的变量值; 最后, 在包含有第一类中间过渡点和上游点的l1曲线上, 由已求得的第一类中间过渡点变量值, 再次应用一维拉格朗日插值, 求出三维空间拉格朗日上游目标点变量值。由图 2所示, 中间过渡点坐标确定后, 将求解区域所有中间过渡点的变量一次插值计算完成, 保留中间过渡点的计算结果, 供后续计算使用。在曲线上应用一维拉格朗日插值求解目标点, 变量为距离, 当选取的插值点越多, 重复利用中间计算结果的比率也越高, 其运算量与传统方法相比约在O(N) 量级。

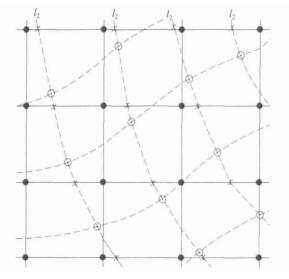
图 2. 欧拉网格与拉格朗日网格 在z(n) 平面构成的网格 (实线代表欧拉网格, 虚线拉格朗日网格; ●代表欧拉网格点; x为第二类中间过渡点; ⊙为第一类中间过渡点; l2为第一类和第二类中间过渡点构成的曲线) Fig 2. Schematic illustration of Eularian grid (solid lines) and Lagrange grid (broken lines) at z(n) panel (● presents nodes of the Eularian grid; x is the second intersection points; the first intersection is marked by ⊙ points; l2 curves composed of the first intersection points and the second points)

2 Cascade插值过程

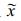
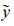
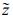
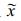
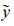
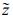
已知欧拉网格点{ x(i), y(j), z(k) }的离散值为f(x(i), y(j), z (k)), 插值求解拉格朗日网格点{ (i, j, k), (i, j, k), (i, j, k) }的函数值F((i, j, k), (i, j, k), (i, j, k)), 其计算过程如下:

① 确定第一类中间过渡点位置

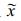
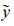
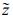
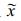
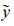
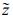
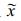
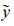
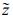
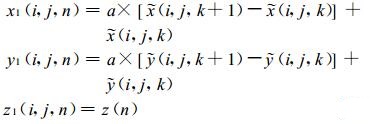
i和j不变, k变化, 逐点用直线连结拉格朗日网格点{ (i, j, k), (i, j, k), (i, j, k) }, 形成曲线l1, 然后求l1与z=z(n) 欧拉网格平面的交叉点{ x1(i, j, n), y1(i, j, n), z1(i, j, n) }, 此交叉点为第一类中间过渡点, 该点是{ (i, j, k), (i, j, k), (i, j, k) }和{(i, j, k+1), (i, j, k+1), (i, j, k+1) }连线之间的点。可求得其坐标:

(8)

其中,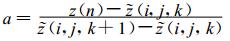

l1上有拉格朗日网格点和第一类中间过渡点, 第一类中间过渡点{ x1 (i, j, n), y1(i, j, n), z 1 (i, j, n) }在欧拉平面z(n) 上的坐标可表示{ x1 (i, j, n), y1(i, j, n) }

② 确定第二类中间过渡点位置

i和n固定不变, j变化, 在z=z(n) 欧拉平面上, 将第一类中间过渡点{ x1(i, j, n), y 1(i, j, n) }逐点直线连成一条曲线l2, 然后求l2与y=y(m) 欧拉网格线的交点, 得到第二类中间过渡点的坐标{ x2(i, m, n), y2(i, m, n) }, 该点是{ x1(i, j, n), y1(i, j, n) }和{ x1(i, j+1, n), y1(i, j+1, n) }连线之间的点, 其计算公式为:

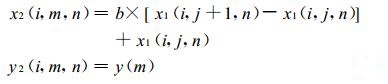
(9)

其中,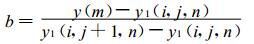

③ 插值求解第二类中间过渡点上的函数值

在z=z(n) 欧拉网格平面, y=y(m) 欧拉网格线上, 求第二类中间过渡点{ x2(i, m, n), y2 (i, m, n) }的函数值f2(x2(i, m, n), y2(i, m, n)), 其为:

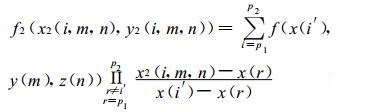
(10)

④ 插值求解第一类中间过渡点上的函数值

在z(n) 上, 沿曲线l2, 利用求得的第二类中间过渡点{ x2(i, m, n), y 2(i, m, n) }的函数值f 2(x2(i, m, n), y 2(i, m, n)) 插值第一类中间过渡点{ x1(i, j, n), y1 (i, j, n) }的函数值f 1 (x1 (i, j, n), y 1 (i, j, n))。

(a) 曲线l2上点{ x1(i, j, n), y1(i, j, n) }介于{ x2(i, m, n), y2(i, m, n) }和{ x2(i, m+1, n), y2(i, m+1, n) }之间。定义沿曲线l2的{ x2(i, m, n), y2(i, m, n) }相对{ x2 (i, m1, n), y2(i, m1, n) }的距离为Sm, 当m取值范围为[m1, m2], 设Sm1=0

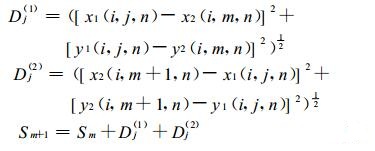
(11)

(b) 沿曲线l2, 第一类中间过渡点{ x1(i, j, n), y1(i, j, n) }相对点{ x2 (i, m1, n), y2(i, m1, n) }的距离为:

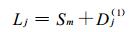
(12)

(c) 以曲线距离作为独立变量, 沿曲线l2作拉格朗日多项式插值, 求第一类中间过渡点{ x1(i, j, n), y1(i, j, n) }上的函数值为:

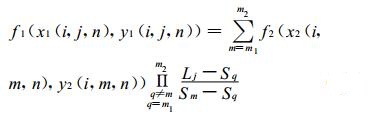
(13)

⑤ 插值求解拉格朗日格点 (目标点) 的函数值

沿曲线l1, 利用所求得的第一类中间过渡点{ x1(i, j, n), y1(i, j, n), z1(i, j, n) }的函数值计算拉格朗网格点 (目标点) 的函数值。

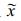
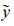
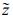
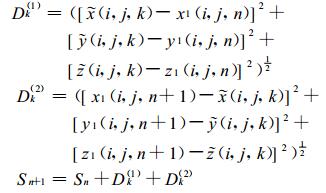
(a) 沿曲线l1, 拉格朗日格点{ (i, j, k), (i, j, k), (i, j, k) }是介于点{ x1 (i, j, n), y1 (i, j, n), z 1(i, j, n) }和{ x1(i, j, n+1), y 1(i, j, n+1), z 1(i, j, n+1) }之间的点, 定义沿曲线l1的点{ x1(i, j, n), y 1(i, j, n), z1(i, j, n) }相对点{ x1(i, j, p1), y1(i, j, p1), z1(i, j, p1) }的距离设为Sn, 当n取值范围为[p1, p2], 设Sp1=0, 那么

(14)

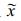
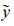
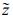
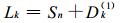
(b) 沿曲线l1, 拉格朗日格点{ (i, j, k), (i, j, k), (i, j, k) }对应的距离为

(15)

(c) 以曲线距离作为独立变量, 沿曲线l1作拉格朗日插值, 求拉格朗日格点上的函数值为:

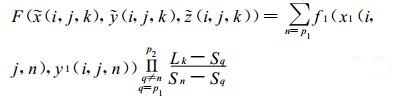
(16)

GRAPES模式并行计算采用水平分区计算的方式[16], 按经纬度划分各个子区域, 将全区域各场的计算分解到各子区域计算, 各子区域计算分别影射到并行环境中的各个计算节点, 每个节点通过一定规则进行数据交换和信息传递以组织并行计算。各节点执行相同的程序结构, 仅仅是操作数据不同。Cascade插值技术中, 如果对于一维曲线插值, 从曲线上各点相对起始点累计计算距离变量, 使各节点计算产生依赖关系, 即各计算节点上的运算依赖于其他节点的计算结果, 实现并行计算非常不方便。因此, 曲线上插值目标点, 根据插值节点数目, 在目标点两边选取相同数目的插值点 (第一或第二类中间过渡点), 一次全部计算过目标点相邻插值点之间的距离, 然后以累计方式计算插值点之间的相对距离, 确定距离变量, 这样有利于不同节点数据交换。

在预报模式中应用拉格朗日多项式, 插值节点数的选择对精度和计算效率有重要的影响, 拉格朗日多项式插值次数低精度不能满足要求, 高次插值耗费计算机机时, 考虑精度和计算成本, 选择三次插值是一种好的折中方案[1]。

3 Cascade插值在GRAPES模式中的应用

GRAPES模式在三维空间求解拉格朗日上游点变量, 采用一系列一维三次多项式插值, 其中间过渡点及上游点的值均使用三次多项式插值法求得。对Cascade插值技术与传统的Cartesian乘积技术在GRAPES模式中进行运行比较, 以垂直分层为31, 水平分辨率50 km×50 km, 720×360个格点与水平分辨率100 km×100 km, 360×180个格点两个例子做实验。GRAPES模式在IBM-cluster 1600大型计算机中运行时, 在模式程序中对拉格朗日插值代码每积分步都进行CPU运算时间监控, 以此获得定量的结果。运算结果表明Cascade方案比传统方案平均节省运算量大约在30%

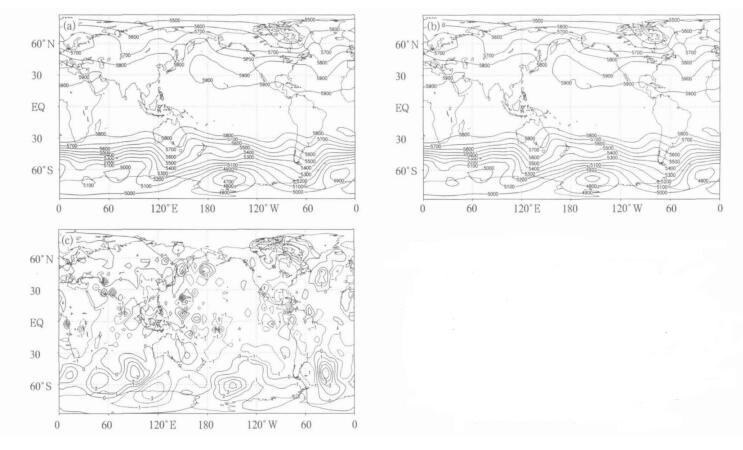
另外, 采用不同插值方法后对预报结果产生的影响进行了对比。选取个例初值为2005年7月18日12:00(世界时), 以48 h预报结果为例, 两种插值对于500 hPa高度场预报产生差别可忽略不计, 最大偏差仅为5 gpm (图 3)

图 3. 采用不同插值方法48 h预报, 500hPa位势高度及偏差 (单位：gpm) (a) 传统Cartesian插值, (b) Cascade插值, (c) 两种插值方法预报500 hPa位势高度偏差 Fig 3. An example of 48-hour 500hPa geo-potential height forecast using Cartesian product and Cascade interpolation technique (unit:gpm) (a) the convention Cartesian-product interpolation, (b) the Cascade interpolation scheme, (c) the difference of 48-hour 500 hPa geo-potential height forecast using two methods

4 小结

从插值过程分析, Cascade插值方法与传统逐点插值方法对比, 相对比较复杂, 主要表现在确定中间过渡点上。传统逐点插值方法是经过三维空间插值目标点, 分别做x, y, z轴平行线或投影在平面和坐标轴上确定坐标, 虽然中间过渡点坐标容易求得, 但涉及到目标点或拉格朗日上游点插值计算时, 对每个计算点都要进行中间过渡点插值计算, 各三维空间目标点插值相互孤立, 中间过渡点插值结果不能为其他点插值所利用, 要重复计算中间过渡点的变量值。而Cascade插值使相邻被插值点和中间过渡点处于曲线上, 中间过渡点插值结果可重复利用, 减少了插值中间过渡点的运算量。将Cascade插值方法应用到GRAPES模式中与传统逐点插值相比较, 得到以下结论:

1) 虽然Cascade插值方法增加了一些中间运算量, 但是在GRAPES模式中采用三次多项式插值计算, 比传统逐点直线插值运算效率大幅度提高。

2) Cascade插值方法应用于GRAPES模式在节省运算量的同时, 不降低插值精度。

3) GRAPES模式中半拉格朗日计算时间约占整个模式运算的30%, 其中插值计算在半拉格朗日计算中占据较大比例, Cascade方法应用对整个模式可以节省大量运行时间。

另外, Cascade插值技术在GRAPES全球模式应用中, 在曲线上计算插值点之间的相对距离, 应是曲线最短距离。对于判断是否为最近距离, 不在Cascade插值过程中进行, 应在插值运算之前确保在拉格朗日格点沿轴方向曲线上各点坐标相对轴为最近距离坐标, 这样可减少附加计算量, 充分凸显Cascade插值方法的优势。

致谢 应用Cascade插值方法在GRAPES模式实现过程中得到了中国气象科学研究院杨学胜、张红亮等同仁的帮助; 同时, 中国气象科学研究院数值预报研究中心为本文提供了很好的工作平台, 在此表示感谢。
参考文献
[1] Staniforth A, Cote J, Semi-Lagrangian integration scheme for atmospherle models-A review. Mon Wea Rev, 1991, 119: 2206–2223. DOI:10.1175/1520-0493(1991)119<2206:SLISFA>2.0.CO;2
[2] Bermejo R, Staniforth A, The conversion of semi-Lagragian advection scheme to quasi-monotone scheme. Mon Wea Rev, 1992, 120: 2622–2632. DOI:10.1175/1520-0493(1992)120<2622:TCOSLA>2.0.CO;2
[3] McDonald A, Accuracy of multiply-upstream, semi-Lagrangian scheme Ⅱ. Mon Wea Rev, 1987, 115: 1446–1450. DOI:10.1175/1520-0493(1987)115<1446:AOMUSL>2.0.CO;2
[4] Purser R J, Leslie L M, An efficient interpolation procedure for high-order three-dimensional semi-Lagrangian models. Mon Wea Rev, 1991, 119: 2492–2498. DOI:10.1175/1520-0493(1991)119<2492:AEIPFH>2.0.CO;2
[5] Bates J R, Semazzi F H M, Higgins R W, et al. Integration of the shallow-water equations on the sphere using a vector semi Lagragian scheme with a multi-grid solver. Mon Wea Rev, 1990, 118: 1615–1627. DOI:10.1175/1520-0493(1990)118<1615:IOTSWE>2.0.CO;2
[6] Purser R J, Leslie L M, An efficient semi-Lagrangian scheme using third order semi implicit time integration and forward trajectories. Mon Wea Rev, 1994, 120: 745–756.
[7] Nair Ramachandran, Cote J, Staniforth Andrew, Monotonic cascade interpolation for semi-Lagrangian advection. Q J R Meteorol Soc, 1999, 125: 197–212. DOI:10.1002/(ISSN)1477-870X
[8] Rancic M, An efficient, conservative, monotone remapping for semi-lagrangian transport algorithm. Mon Wea Rev, 1995, 123: 1213–1217. DOI:10.1175/1520-0493(1995)123<1213:AECMRF>2.0.CO;2
[9] 陈德辉, 杨学胜, 张红亮, 等. 多尺度非静力通用模式框架的设计策略. 应用气象学报, 2003, 14, (4): 452–461.
[10] 杨学胜, 陈嘉滨, 胡江林, 等. 全球非静力半隐式半拉格朗日模式及其极区离散处理. 中国科学 (D辑):地球科学, 2007, 37, (9): 1267–1272.
[11] 陈嘉滨, 季仲贞. 半隐式半拉格朗日平方守恒计算格式的构造. 大气科学, 2004, 28, (4): 527–535.
[12] 薛纪善. 新世纪初我国数值天气预报的科技创新研究. 应用气象学报, 2006, 17, (5): 602–610.
[13] 陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 2006, 17, (6): 773–777.
[14] 胡江林, 沈学顺, 张红亮, 等. GRAPES模式动力框架的长期积分特征. 应用气象学报, 2007, 3: 276–284.
[15] Sun Wen-yih, Kao-san yeh, A general semi-Lagrangian advection scheme employing forward trajectories. Q J R Meteorol Soc, 1997, 123: 2463–2476. DOI:10.1002/qj.v123:544
[16] 伍湘君, 金之雁, 黄丽萍, 等. GRAPES模式软件框架与实现. 应用气象学报, 2005, 16, (4): 539–546.