应用气象学报  2009, 20 (2): 129-136   PDF    
引用本文
罗阳, 赵伟, 翟景秋. 两类天气预报评分问题研究及一种新评分方法[J]. 应用气象学报, 2009, 20(2): 129-136.
Luo Yang, Zhao Wei, Zhai Jingqiu. Dichotomous Weather Forecasts Score Research and a New Measure of Score[J]. Journal of Applied Meteorological Science, 2009, 20(2): 129-136  
两类天气预报评分问题研究及一种新评分方法
罗阳1, 赵伟2, 翟景秋1     
1. 中国人民解放军 61741 部队气象中心, 北京 100081;
2. 中国人民解放军 63880 部队气象室, 洛阳 471003
2008-04-08 收到, 2008-12-11 收到修改稿.
摘要: 探讨了预报评价的意义及应遵循的原则, 对常用的几种两类预报评分方法进行分析, 指出其应用的局限性, 得到一个判定所作预报水平是否高于随机预报、具有预报技巧的简易判别式; 提出评分权重的概念, 指出以往评分存在问题的根源是评分权重分配不当, 使评分结果的真实性受到影响, 评分无可比性, 进而提出一种考虑了评分权重的新评分方法。新评分方法满足预报评价的原则, 侧重于对两类事件中事件概率较小一方预报效果的评估, 评分结果不受事件概率影响, 具有可比性。对比分析表明:新方法比其他方法优越, 能更准确地反映预报水平, 使不同季节、不同地域的预报评分可进行比较, 是一个通用的评分方法。
关键词: 预报评价    技巧评分    评分权重    概率    可比性    
Dichotomous Weather Forecasts Score Research and a New Measure of Score
Luo Yang1, Zhao Wei2, Zhai Jingqiu1     
1. Meteorological Center of PLA 61741 Army, Beijing 100081;
2. Meteorological Department of PLA 63880 Army, Luoyang 471003
Abstract: The significance of forecast estim ate and the principles are discussed. It is assumed that the scores are objective; and moreover they can objectively reflect the forecast level.The scores should be comparable, guiding forecast in the right direction. Several usual methods of dichotomous forecasts score are analyzed, revealing that accuracy and critical success index (CSI) in different areas are incomparable due to the influence of event possibility. It shows that the true skill statistic (TSS) is approach to the probability of detection (POD) when forecasting rare events.When events do not appear but false alarms are made, TSS can't be calculated. Heidke skill score and Girbet skill score make up for the above weaknesses. The three skill scores are all obtained by comparing forecast with random ones, hence there are (n11n22-n12n21) in the three formulas. It can be used as the discriminant for forecast skill. When (n11n22-n12n21)> 0, it indicates that the forecast level is better than that of random forecast, otherwise, it will be worse than it. On the basis of the relationship between event probability and the difficulty of forecast, a new method of score weight is considered and proposed. The essay points out the exiting problems are resulted from improper score weight, leading the score result unreliable and not comparable. The new method of score is based on CSI, and combines CSI of the two event forecasts. The focus of score is laid upon estimating the one with smaller probability in the two events.The principles of forecast score are fulfilled. By comparative analysis, the new method is proved to be superior to other methods, especially on estimating rare events. They can reflect the forecast level and changes more accurately.The advantages are as follows :With the increase of samples, the new score tends to be more stable than other scores in the rare events fo recast, thus leading to a rapid judgement for forecast level. When forecast level is improved, the new score will be able to reflect it correctly and distinctly. The new score is objective, just and real, and is compatible for different seasons and regions. So it is a uniform standard in forecast score.
Key words: forecast estimate     skill score     score weight     probability     comparable    
引言

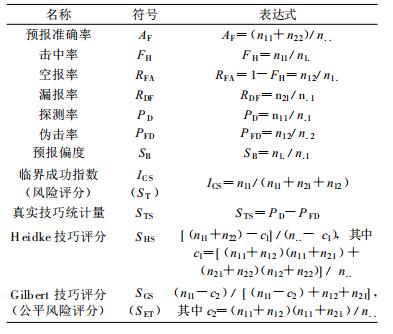
天气预报检验随着天气预报的产生而产生。1850 -1870年, 美国和西欧几个国家开始了基于实时天气图的天气预报业务[1-2], 随之而来的是关于这些预报产品质量的疑问或争论, 如在19世纪60年代初期, 就有许多关于英国气象部门对风暴预警准确率的评价文章[3]。然而, 1880年以前, 这些预报检验的实践, 无论从概念上还是方法上都没有引起人们的重视。

1884年, 美国陆军信号兵Finley军士对美国中东部的龙卷风预报, 用他本人提出的“准确率”评分方法进行了检验评估, 并发表了论文[4], 由此引发了1884 -1893年间人们对预报评价工作的关注, 推动了预报评价概念的建立及方法的研究, Finley的预报试验也成为许多教科书和文章中阐述预报评分时常引用的典型案例[5]。

在Finley的论文发表后6个月内, 有3个人发表文章指出了Finley评分方法的不足, 并提出了自己的评分方法:第一位是Gilbert, 仅仅在两个月后就发表了论文[6], 提出了一种评分方法, 后被Palmer等[7]重新发现并命名为风险评分TS (threat score), 再被Donaldson发现并命名为临界成功指数CSI (critical success index) [8], Gilbert同时还提出了修正的CSI评分, 即Gilbert技巧评分GSS (Gilbert skill score), Schaefer[9], Black[10]后来也分别发现了这一技巧评分, 后者称其为公平风险评分ETS (equitable threat score); 第二位是Price, 他提出了一种技巧评分方法[11], Hanssen等[12]提出了与之近似的所谓HK判别式 (Hanssen-Kuipers discriminant) 或称Kuipers成绩指数 (Kuipers's performance index) [13], Flueck在1987年提出了与Peirce技巧评分相同的所谓真实技巧统计量TSS (true skill statistic) [14]; 第三位是Doolittle[15-16], 先后提出了两种技巧评分, 后一种就是现在使用的Heidke技巧评分HSS (Heidke skill score) [17]。

1884 -1893年提出的这些评分方法至今仍然使用着, 百余年来不断有人重新发现并命名, 但关于预报检验的概念和方法并没有什么改变。如今, 在预报评价方面存在着评分方法使用不当, 不能准确评价预报水平的问题。比如, 预报评价工作中使用准确率 (或称正确度、预报效率EH) 评分, 不加条件地使用临界成功指数ICS(风险评分ST) 的情况经常出现。本文在前人研究的基础上, 重新审视了预报评价的意义与原则, 以新的视角、Finley等人实践数据及假设的试验数据, 对常用的评分方法进行了分析讨论, 并提出一种优于以往评分的新方法。

1 预报评价的意义和原则

预报评价的意义主要包括以下3个方面:一是对预报质量进行监控; 二是通过质量监控发现问题, 改进预报质量; 三是比较不同预报系统 (方法) 的质量[18]。

Murphy[19]认为对预报评价应从3方面考虑: ①一致性, 即预报员的判断与预报结论的一致性。比如, 一个预报员认为第二天要出现雷暴天气, 但由于某种原因 (比如预报得分的高低) 没报雷暴而报了阵雨, 而第二天确实出现了阵雨天气, 这时虽然报对了, 但预报思维与结论是不一致的。②质量, 即预报与实际观测的符合程度。③价值, 即预报产品是否给使用者带来了利益。如果预报对以上条件都满足, 则说这次预报是成功、完美的预报。

人们总是希望能计算一种或多种的评价度量指标, 以便对预报质量进行客观公正的评估。度量指标应该满足如下要求:使天气预报的评估过程对预报员 (或系统) 的任何不利影响达到最小, 并能够对不同预报样本的预报结果进行横向比较[20]。也就是说, 一种评分方法, 应避免预报员为获取高分而做出不合理的预报, 不同地区的预报结果可以互相比较, 不受事件概率的影响。

根据上面的讨论, 以及Flueck、丁金才和新田尚等人对评分原则的研究[14, 21-22], 本文认为, 评价标准应满足以下4个原则: ①评分标准要客观; ②评分结果真实反映预报水平; ③评分要有可比性; ④要避免预报员为获取高分而产生错误的预报倾向。

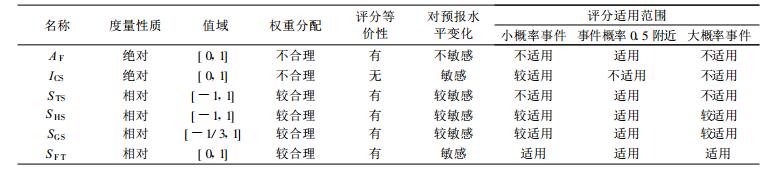
2 评价度量的性质

目前, 评价标准 (方法) 很多, 从性质上可分为两种, 一种是绝对度量, 另一种是相对度量。绝对度量是样本中预报值和观测值的函数, 度量预报值与观测值之间的差异, 如平均绝对误差、预报与实况的相关系数、准确率FP评分等, 它仅考查预报本身的准确性, 并未考虑技术上的优劣, 所以, 这种度量不具有可比性; 而相对度量则是样本数量以及与参考系统相联系的预报和观测的函数, 是一个样本的预报质量相对于参考系统得出的预报质量的度量, 从而可以显示预报技巧, 这种度量一般叫技巧评分, 而参考预报, 一般是随机预报、气候预报或是持续预报。若以S表示某预报的评分, Sref表示参考预报的评分, Sperf表示理想预报评分, 则技巧评分SS的一般形式为: SS=(S-Sref)/(Sperf-Sref) [20]。

对于“有”、“无”或“出”、“不出”等两类事件的评价度量, 还应满足“事件等价性”的要求, 即对一类事件的预报评分应与对另一类事件的预报评分相同。比如, 对雷暴预报的样本进行评分, 则对“预报雷暴出不出”的评分, 应与对“预报无雷天气出不出”的评分相等。

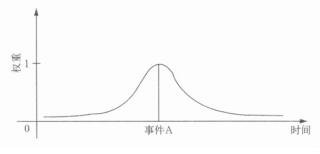
3 评分权重概念的引入

事件预报的难度与其概率有关, 当事件概率较小时, 预报难度较大, 报对时应该给予较多的得分, 即预报难度大, 应给予较大的评分权重; 反之, 当事件概率较大, 预报难度较小时, 则应给予较小的评分权重, 因此, 在设计评分方法时, 应考虑所报事件的难易程度而给予相应权重得分。图 1显示了事件A (假设是小概率事件) 及其附近预报日应有较高的得分权重, 而离A越远, 越容易报对, 得分权重也就越小, 其变化应是指数型的。实际预报中也是这种情况, 一般而言, 雷暴日附近的几天中, 预报雷暴“出”与“不出”总是比远离雷暴日的时候难报, 所以, 在评分中引入评分权重的概念是正确的, 符合客观实际。

图 1. 事件A的评分权重分布示意图 Fig 1. Score weight distribution of Event A

4 对已有评分方法的讨论

表 1为两类预报评分常用列联表[23]。

表 1 两类预报列联表 Table 1 Contingency table for dichotomous (yes/no) forecasts

根据表 1中的数据, 相应有表 2所示的各种评价统计量。

表 2中有一些评分统计量经常用到, 如事件的空报率、漏报率和预报偏度等, 这类统计量只是反映事件预报某方面的问题, 如事件预报偏多还是偏少, 不能对预报水平 (技术) 做出整体评价, 本文重点讨论对预报整体进行评分的统计量, 即常用的预报准确率AF、临界成功指数ICS(即ST评分) 及一些技巧评分, 下面以Finley龙卷预报为例 (表 3), 对这些评分方法进行分析。

表 2 两类预报评价方法 Table 2 Verification methods for dichotomous (yes/no) forecasts

表 3 Finley预报列联表 Table 3 Contingency table for Finley's forecasts

4.1 预报准确率

预报准确率AF[4]表示预报成功次数 (不论预报“有”、“无”) 与总预报次数之比。将表 3中的数值代入表 2的表达式, 计算得到AF=(28+2680)/2803×100%=96.61%, 但这个分数说明不了龙卷风的预报水平, 这个得分甚至不如天天报无龙卷风的得分高 (此时AF=(2803-51)/2803×100%=98.18%), 而这种预报无任何技术可言, 由此可见, 准确率不能代表预报的真实水平, 因为它没有与参考预报 (比如上面的“天天报无龙卷风”的预报方法) 进行对比, 是一个绝对度量, 而不是相对度量, 无法反映预报技巧。问题在于, 它将2680次无龙卷风预报成功的次数算为龙卷风预报的成功次数, 这显然夸大了预报水平。这相当于将事件“出”与“不出”的两类预报效果进行了等权重考虑 (权重比为1:1), 认为同样重要, 这显然不对。从这里也可以看出, 与参考预报进行对比的过程, 实际上就是提高事件预报成功的权重, 而降低非事件预报成功的权重过程。所以, 由于准确率对“出”与“不出”两事件进行等权重的考虑, 在大概率事件或小概率事件的预报中, 预报员可以不加分析多报大概率事件而取得较高的分数, 这不能代表预报水平, 这种错误倾向是应该避免的。只有当事件概率接近0.5时, 准确率才能较好地代表预报水平。对于两类预报而言, 准确率评分满足事件等价性的要求, 比如本例中, 不论是对龙卷风的预报, 还是对非龙卷风的预报其评分是一样的。

4.2 临界成功指数

临界成功指数ICS [8]常用于小概率事件, 比如灾害性天气预报的评定。将表 3中的数值代入表 2的表达式, 计算得到ICS=28/(28+23+72)=0.228, 它与n22的大小无关, 表示它对事件“出”与“不出”的两类预报效果的考虑权重比为1 : 0。ICS根本没有考虑n22的影响是不妥的, Doswell等[24]认为, n22中的大多数预报对预报验证价值不高, 然而, n22中有一些预报是应该得分的, 正如许多预报员所抱怨的, 有时作了很大的努力报对了“事件不出”的预报, 却对预报评分没有任何正面的影响, 这是ICS的潜在问题。

因为ICS没有与参考预报进行比较, 所以不能排除事件概率的影响, 事件概率高的地区, ICS往往偏大。但对于小概率事件预报, 可以认为各事件的概率相差不大, 且认为n22对评分的贡献很小, 可不计, 所以, 此时可以用ICS进行评分并可进行相互间的比较。

ICS评分对两类预报问题不满足等价性。比如表 3中, 龙卷风预报的ICS=0.228, 非龙卷风预报的ICS=2680/(2680+23+72)=0.966。

4.3 技巧评分

下面对表 2中后3个评分统计量进行讨论, 因它们都与参考预报进行了对比, 所以是反映预报技术的技巧评分。

4.3.1 真实技巧统计量STS[14]

它表示对事件的探测能力, 即区分事件“有” “无”的能力, 其值域为[-1,1], 预报完全正确时, STS=1。STS的等价表达式为

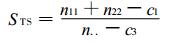
(1)

式 (1) 中, c1含义同表 2, 表示随机预报的正确次数, c3=[(n11+n21) (n11+n21) +(n12+n22) (n12+n22)] /n.., 表示气候预报的正确次数, 可见STS是实际预报与某种参考预报进行对比得出的。1990年, Doswell等[24]发现在对小概率事件预报时, STS值趋近于PD会导致过分预报事件“出”的倾向。因为此时, PFD=n12/n.2值趋近于0, 预报员不怕空报, 就怕漏报, 一有事件出现征候就报事件出, 其结果是这种错误倾向的预报却可能有一个较高的得分, 不符合评分原则的第4条另外, 对于无事件出现, 却有空报的预报过程, 无法用STS评分。

4.3.2 Heidke技巧评分SHS [17]

它用到的参考预报c1是随机预报, 表示实际预报的准确率比随机预报的准确率好多少, 其值范围在[-1,1]之间, 预报完全正确时, SHS=1。

4.3.3 Gilbert技巧评分SGS[6]

它用到的参考预报c2也是随机预报, 只不过是针对事件“出现”的随机预报。SGS实际上是ICS评分扣除随机预报正确次数得到的, 所以, SGS也叫做技巧临界成功指数, 其值范围在[-1/3,1]之间, 预报完全正确时, SGS=1。

当这3种评分不高于0时, 表示实际预报不如或者等于随机预报的效果, 当这3种评分高于0时, 表示实际预报水平大于随机预报水平, 有一定的预报技巧。

这3种评分的另一种表达式如下:

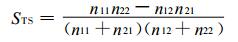
(2)
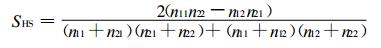
(3)
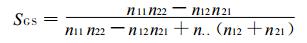
(4)

由式 (2)~(4) 可以看出, 它们的分母皆大于0, 分子都有n11 n22-n 12n21项, 所以, 通过该项是否大于0的判定, 可迅速判断预报水平是否高于随机预报水平, 因此, n11n22-n12n21可作为预报水平的一个定性判据; 可以看出, 预报对象互换后评分仍相同, 说明这3种技巧评分满足事件等价性的要求。由于等价性, STS评分不仅对小概率事件预报不适用, 对大概率事件预报也不适用。

从上面对以往评分的讨论可知, AF和ICS评分中评分权重分配不合理, 不适合对预报技术进行评价, 而后面的3种技巧评分, 通过与参考预报进行比较, 降低了气候概率影响, 相当于权重有了新的分配。但这种与参考预报比较后的统计量, 是否能准确地反映预报技术, 下面通过与一种新的评分方法进行对比分析, 做进一步的研究。

5 一种新的评分方法

从上面的分析可以看出, 评分中存在的主要问题就是事件的评分权重问题。以往评分对于事件“不出”预报结果, 不是考虑的太重 (权重为1), 就是考虑的太轻 (权重为0), 此权重值应该根据事件概率的大小取相应的值。因此, 需要设计一个新的评分统计量, 它能够根据事件概率大小自动调节评分权重。

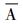
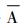
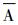
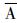
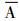
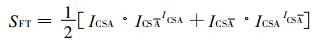
新评分的设计思路及其物理意义是:当事件A的概率较小时, 非事件的数量必然很多, 这其中必有许多与A的相关性非常小, 很容易对其预报, 比如, 晴天报无雨要比多云、阴天报无雨容易, 因此评分的重点应放在“事件A”的预报结果上, 弱化的预报效果; 当事件A的概率较大时, 预报相对容易, 易有较高的得分, 但这并不能真实反映预报水平, 要弱化A的预报效果, 评分的重点应放在“非事件”的预报结果上。从前面的分析可知, 对小概率事件的预报ICS较好用, 以其为基础并进行改造, 以满足上面的要求, 则事件A的评分可设计为ICSA ·(ICSA) ICSA的形式, 考虑到两类事件预报的等价性, 最后的评分取A评分与评分的均值, 由此得到式 (5) 所示的新评分方法。为与其他评分方法区别, 称其为预报技术评分SFT(forecast technique score)

(5)

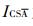
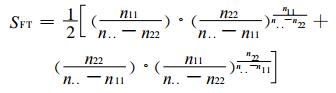
式 (5) 中, ICSA为A事件的ICS评分, 为非A事件的ICS评分。SFT也可用下式表示:

(6)

从式 (6) 可以看出, 只知道了事件预报“出”与“不出”的正确次数和预报的总次数即可进行评分, 不需要知道空、漏报的情况, 较以往的技巧评分简单。由于引入了评分权重的概念, 对大概率事件预报引起的评分虚增现象进行了权重“过滤”处理, 因此, 该评分也是一种技巧评分, 它虽然没有与参考预报进行对比来显示预报技巧的高低, 但它通过权重处理的过程达到了衡量预报技术高低的目的。

SFT评分具有如下性质:

①预报完全正确时, SFT=1;预报完全错误时, SFT=0。

预报完全正确时分两种情况, 一种情况是预报过程中两类事件都全部报对, 此时有n.1≠ 0, n.2≠0, 且没有空报或漏报, 即n12=n21=0, 此时n..=n11+n22, 所以有

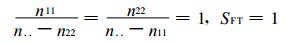
另一种情况是预报过程中只出现了一类事件且全部报对 (假设为事件1), 则有n12=n21=0, n22=0, n11=n..≠0, 此时有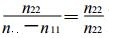为0/0的不定式情形, 这在数学上是无意义的, 而对预报评价而言, 对这种“完全正确”的预报评价也是无意义的, 因为这看不出预报水平, 等同于盲目预报。对于这种情况, STS, SHS, SGS也会出现0/0的情形, 说明这种情况无论用哪种评分都是无意义的, 现实中也很少出现此情况。

预报完全错误时也分两种情况, 第一种情况是两类事件中, 无论哪类事件没有一次报对, 即n11=n22=0, 代入式 (6) 可得

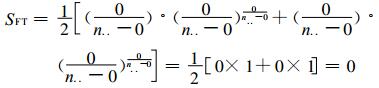
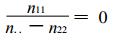
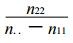
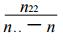
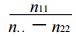
第二种情况是两类事件中有一类事件一次都没有报对, 而另一类事件至少报对了一次, 即n11=0且n22 ≠0或n22=0且n11 ≠0的情况, 因此有且≠ 0, 或=0且≠0代入式 (6) 可知SFT=0。严格说, 这种情况不能说完全报错, 因为有n22≠0或n11 ≠0。但是, 这种预报效果甚至不如一种参考预报---“单向预报”(即根据气候概率大小, 始终报两类事件中气候概率大的事件) 的效果, 而且, 这种预报也没有体现出区分两类事件的能力, 从这个意义上说, 这种预报是“完全错误的”, 不应得分。比如, 60 d当中出了3 d雷暴, 一次没有报出, 却有空报和漏报 (肯定是漏报3次), 这种预报不比60 d每天都报无雷暴效果好。因此, 第二种情况的预报不如参考预报, 无技术可言, 给予0分是合理的。

② SFT满足等价性的要求, 两类事件互换后评分仍相同。

从式 (6) 可以看出, n11和n22位置互换后, SFT值不变。

③ SFT通过指数的调节作用, 合理分配权重, 消除了事件概率的影响, 使评分具有可比性。

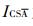
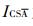
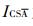
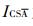
从图 2可以看出SFT与ICSA, 的相互关系, 当ICSA() 较小时, 随着(ICSA) 的增大, SFT迅速趋于ICSA(), 可见, SFT重点是对两类事件预报中ICS较小一方的预报效果进行评价, 与事件A的概率大小无关, 这也提醒预报员应将研究重点放在提高小的ICS对应事件的预报水平上。

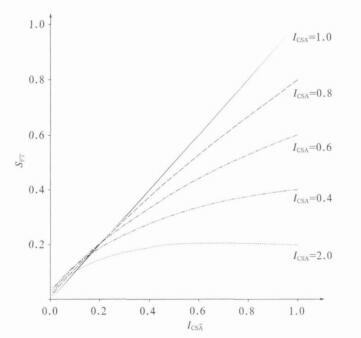
图 2. SFT与ICSA, 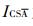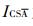相互关系示意图 Fig 2. Interrelation for SFTtoICSAand

④ SFT评分拓展了ICS评分的适用范围, 对小概率事件两者差异很小。

SFT评分来源于ICS, 但优于ICS, 它适用于任何事件概率的评分。通过以下实例和证明, 将看到两者之间的关系。表 4中的数据取自文献[4, 25-26], 为实际预报结果。从表 4中可以看出, 随着事件概率的减小, n22相对其他3个量显得更大, 这与一般的预报实践是吻合的。同时, 可以看出, SFT与ICS也更接近。从龙卷风的预报中可以看出, 当n22比其他3个量大很多时, SFT≈ICS。

表 4 预报实例及评分研究 Table 4 Examples of forecast and score research

从式 (6) 可以看出, 当n22较大时,

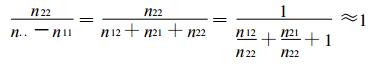
所以有

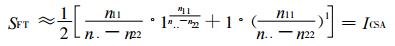
(7)

这也说明了ICS只适用于小概率事件预报问题的原因, 因为此时两者差异不大。

⑤因为能合理分配两类事件的评分权重, SFT反映预报水平比其他技巧评分更准确。主要表现为:预报水平相近时, 不同预报试验的评分, SFT的波动小于其他评分; 当预报水平较低时, SFT能克服n22增大过程中带来的评分虚增现象, 更快地确定预报水平; 当预报水平提高时, SFT比其他评分反映更加敏感、准确。

比如, 对表 5中的试验数据, 假设当F1预报水平有所提高, 事件多报对了2次, 即试验F1a, 可见F1a的SFT得分要大于F2, 而其他3个技巧评分却不如F2试验的得分高。F2只是事件不出现的预报正确数增加了, 而事件出现的预报正确数没变化, 可见SFT评分可准确反映预报水平的变化, 评分重点始终着眼于难报的事件, 对预报有正确的导向, 说明评分权重的分配是合理的。

表 5 预报水平变化时各种评对比分析 Table 5 Comparative analysis of scores at changed forecast level

6 评分特性的对比分析

通过上面的分析讨论可知, AF, ICS评分是衡量预报与观测之间的量, 是绝对度量, 考察的是预报与观测的吻合程度, 不同事件概率构成的预报样本, 其评分无可比性, 因此, 这两种评分不能考察预报技术或预报技巧, 也就是说, 它不能排除随机预报或盲目预报得高分的现象。STS, SHS和SGS评分是能显示预报技术或技巧的评分, 因它们与参考预报进行了对比, 将随机预报或盲目预报得高分的现象排除在外, 是一种相对度量, 即相对于参考预报而言, 所作预报的优劣程度, 因此, 这些评分降低了事件概率的影响, 大多数情况下, 评分具有可比性, 只是在小概率事件且预报水平较低时, 评分有偏大的倾向, 对预报水平的变化不敏感。SFT评分通过评分权重的作用, 排除了随机预报或盲目预报等得高分的现象, 也是一种预报技术或技巧评分, 尤其在小概率事件的预报上, 比其他评分更准确地反映预报水平。

总结以上的讨论, 可得各类评分特性如表 6所示。

表 6 各类评分特性分析 Table 6 Characteristic analysis of scores

7 小结

通过对两类预报评分问题的分析研究, 可得到如下结论:

1) 尽量不要使用准确率AF和ICS评分, 尤其在比较不同地区预报水平时。应提倡使用技巧评分, 如Heidke技巧评分、Gilbert技巧评分和本文的SFT评分, 它们能较好地消除事件概率的影响, 使评分具有可比性。

2) Heidke等3个技巧评分, 都是与参考预报-随机预报比较得出的, 都有一个相同的因子项n11n22-n12n21, 通过它是否大于0, 可迅速简便地判断所作预报是否好于随机预报, 是否具有预报技巧。

3) 影响评分, 使之不可比的因素表面上看是事件概率不同以及预报偏度引起的, 实质上是评分权重分配不当造成的。通过引入评分权重的概念, 较好地解决了以往评分存在的问题。

4) 基于评分权重思想提出的新的评分方法, 克服了以往评分的不足。新的评分方法满足了评分的4个原则, 比以往评分对预报水平的评价更真实、更敏感、更严格, 尤其是对低水平预报评分。

评价一种评分方法的优劣, 关键在于它对低水平预报的评价是否真实, 因为正确的评价才会对改进预报质量、提高预报水平有正确的指导意义。而对一个高水平的预报, 各种评分方法优劣却很难比较。新评分的特点就是重点考虑两类事件中数量较少一方的预报水平, 给其以较大的评分权重, 使预报员真正把注意力放在提高难点天气预报水平上, 对预报工作有正确的导向。

参考文献
[1] Hughes P, The great leap forward. Weatherwise, 1994, 47: 22–27.
[2] Whitnah D R, A History of the United States Weather Bureau. Illinois: University of Illinois Press, 1961: 1-267.
[3] Burton J, Robert Fitzroy and the early history of the Meteorological Office. Br J Hist Sci, 1986, 19: 147–176. DOI:10.1017/S0007087400022949
[4] Finley J P, Tornado predictions. Amer Meteor J, 1884, 1: 85–88.
[5] Murphy A H, The Finley affair : A signal event in the history of forecast verification. Wea Forecasting, 1996, 11: 3–20. DOI:10.1175/1520-0434(1996)011<0003:TFAASE>2.0.CO;2
[6] Gilbert G K, Finley's tornado predictions. Amer Meteor J, 1884, 1: 166–172.
[7] Palmer W C, Allen R A, Note on the Accuracy of Forecasts Concerning the Rain Problem. US Weather Bureau, 1949: 1–4.
[8] Donaldson R J, Dyer R M, Krauss M J, An Objective Evaluator of Techniques for Predicting Severe Weather Events. 9th Conf Severe Local Storms, Norman, Oklahoma, Amer Meteor Soc, 1975: 321–326.
[9] Schaefer J T, The critical success index as an indicator of warning skill. Wea Forecasting, 1990, 5: 570–575. DOI:10.1175/1520-0434(1990)005<0570:TCSIAA>2.0.CO;2
[10] Black T L, The new NMC mesoscale eta model:Description and forecast examples. Wea Forecasting, 1994, 9: 265–278. DOI:10.1175/1520-0434(1994)009<0265:TNNMEM>2.0.CO;2
[11] Peirce C S, The numerical measure of the success of prediction. Science, 1884, 4: 453–454.
[12] Hanssen A W, Kuipers W J A, On the relationship between the frequency of rain and various meteorological parameters. Mededeelingen en Verhandelingen, 1965, 81: 2–15.
[13] Murphy A H, Daan H, Forecast Evaluation∥Murphy A H, Katz R W.Probability, Statistics, and Decision Making in the Atmospheric Sciences. Westview: Westview Press, 1985: 379-437.
[14] Flueck J A, A Study of Some Measures of Forecast Verification. 10th Conf Probability and Statistics in Atmospheric Science, Edmonton, Alberta, Amer Meteor Soc, 1987: 69–73.
[15] Doolittle M H, The verification of predictions. Amer Meteor J, 1885, 2: 327–329.
[16] Doolittle M H, Association ratios. Bull Philos Soc Washington, 1888, 10: 83–87.
[17] Heidke P, Berechnung des Erfolges und der Gǜte der Windstärkevorhersagen im Sturmwarnungdienst (Calculation of the success and goodness of strong wind forecasts in the storm warning service). Geogr Ann Stockholm, 1926, 8: 301–349.
[18] Murphy A H, Winkler R L, A general framework for forecast verification. Mon Wea Rev, 1987, 115: 1330–1338. DOI:10.1175/1520-0493(1987)115<1330:AGFFFV>2.0.CO;2
[19] Murphy A H, What is a good forecast? An essay on the nature of goodness in weather forecasting. Wea Forecasting, 1993, 8: 281–293. DOI:10.1175/1520-0434(1993)008<0281:WIAGFA>2.0.CO;2
[20] 张军, 葛军, 田俊杰, 等. 概率天气预报及其应用. 北京: 气象出版社, 1998: 127-137.
[21] 丁金才. 天气预报评分方法评述. 南京气象学院学报, 1995, 18, (1): 143–150.
[22] 新田尚, 立平良三, 市桥英辅.宁松, 译.最新天气预报技术.北京:气象出版社, 1997: 145-146.
[23] Brownlee K A, Statistical Theory and Methodology in Science and Engineering (2nd ed). John Wiley and Sons, 1965.
[24] Doswell Ⅲ C A, Davies-Jones R P, Keller D L, On summary measures of skill in rare event forecasting based on contingency tables. Wea Forecasting, 1990, 5: 576–585. DOI:10.1175/1520-0434(1990)005<0576:OSMOSI>2.0.CO;2
[25] 赵有娟, 赵康林, 王小虎. 涿州地区冬半年辐射雾的预报. 军事气象水文, 2005, (6): 32–33.
[26] 宋伟, 雷显飞, 宋作义. 东北平原夏季雷雨预报. 航空气象, 2005, (2): 31–34.