2009, 20 (1): 108-113
表 1
风电场不同高度的50年一遇最大和极大风速估算
引用本文
呼津华, 王相明. 风电场不同高度的50年一遇最大和极大风速估算[J]. 应用气象学报, 2009, 20(1): 108-113.
Hu Jinhua, Wang Xiangming.
A Method for Estimating the Extreme 10-minute Average and 3-second Wind Speed with a Recurrence Period of 50 Years at the Different Height in a Wind Farm[J]. Journal of Applied Meteorological Science, 2009, 20(1): 108-113
风电场不同高度的50年一遇最大和极大风速估算
新疆金风科技股份有限公司, 乌鲁木齐 830026
摘要: 风电场50年一遇最大和极大风速是决定风电机组极限载荷的关键指标, 也是风电项目开发中机组选型和经济评估的关键指标之一。该文重点从气象学角度, 结合我国风电项目开发的实际情况, 提出5 d最大10 min平均风速取样法, 用Ⅰ型极值概率分布来估算风电场不同高度50年一遇最大风速; 以附近气象站长期的历年最大风速及与风电项目内测风塔同期的逐日最大风速资料, 修正所得结果。再以实测到的大风速段的最大阵风系数, 推算风电场不同高度50年一遇的极大风速。并利用内蒙古巴彦淖尔市乌兰伊力更风电场300 MW项目1年的实测风资料及内蒙古乌拉特中旗气象站的测风资料, 估算乌兰伊力更风电场内不同高度上50年一遇的最大和极大风速。
关键词:
风电场 最大风速 极大风速 Ⅰ型极值概率分布 风电机组 风资源
A Method for Estimating the Extreme 10-minute Average and 3-second Wind Speed with a Recurrence Period of 50 Years at the Different Height in a Wind Farm
Goldwind Science & Technology COLTD, Urumqi 830026
Abstract:
The extreme 10 minute average and 3 second wind speed with a recurrence period of 50 years at the hub height on a wind farm is a major index for choosing the wind turbines types. From the viewpoint of meteorology, and linking some developed examples of the wind farm projects in China, the article brings forward a sampling method of the maximum 10 minute average wind speed of 5 days from a whole year actual measured wind speed data of a mast at the wind farm. The method refers to the typeⅠ extreme value distribution and the modification matrix estimating the parameters method, for estimating the extreme 10 minute average wind speed with a recurrence period of 50 years at different heights in a wind farm. Using the same period and long term wind speed data of a nearby meteorological station, the above results can be revised. Since the distribution of wind resource has its own specialty in China, the maximum gust coefficient is reduced when the wind speed gets larger in north area of China, and is bigger than 1.4 when the wind farm is influenced by tropical storm or typhoon. It suggests that using the actual observed maximum gust coefficient of the bigger wind speed to estimate the extreme 3 second wind speed with a recurrence period of 50 years at different heights in a wind farm. This method is applied to estimate the extreme 10 minute average and 3 second wind speed with a recurrence period of 50 years at the different heights in the Wulanyiligeng wind farm 300 MW project in Bayannaoer City, Inner Mongolia. The result reveals that the method is convenient and reliable for the Wulanyiligeng wind farm projects developing.
Key words:
wind farm
maximum 10-minute average wind speed
extreme 3-second wind speed
the typeⅠextreme value distribution
wind turbines
wind resource
引言
3.3 5 d最大10 min平均风速取样法估算方法的检验
4 小结
我国自2003年开始风电特许权项目以来, 以规模化带动产业化发展, 风电行业在短短的几年时间里有了迅猛的增长, 到2006年年底我国除台湾省外已开发了91个风电场, 风电机组总装机容量近260×104 kW。随着投资、开发和制造主体的多元化和国际化, 我国风电事业的发展面临着空前的机遇, 也有许多急待解决的基础理论问题。风电场不同高度50年一遇最大和极大风速的估算, 就是其中的一个现实基础问题。
由于发展的历史性, 我国有长期资料的气象观测站点相对较少, 取得资料不够统一、详细; 气象站普遍距离拟开发的风电场较远, 且二者的地形地貌差别较大。而风电项目建设必须考虑经济性, 风电场内测风时间不能太长, 又客观地要求对当地风资源做出详尽的分析和评估。
根据国际风电机组设计标准[1]规定, 50年一遇最大和极大风速是决定风电机组极限载荷的关键指标, 也是风电项目开发中机组选型和经济评估的关键指标之一。
现在我国风电项目开发中, 多用《全国风能资源评价技术规定》[2]中的Ⅰ型极值概率分布方法, 估算有长期资料的气象站10 m高度50年一遇最大风速; 以气象站和风电场风速的相关性, 估算出风电场内不同高度50年一遇最大风速; 然后以通常的统计平均阵风系数1.4, 推算风电场内不同高度50年一遇的极大风速。这种方法的问题是, 两地风速的相关性、风电场内不同高度风速的相关性都是随风速的增大而变化的, 不能简单以年平均风速的相关系数来替代, 并且在不同的地区区域内, 阵风系数也随风速变化而有不同的变化。
在参考国内外已经较成熟的极值估算方法的基础上[3-4], 本文从气象学角度, 提出5 d最大10 min平均风速取样法, 用Ⅰ型极值概率分布来估算风电场不同高度的50年一遇最大风速; 并以附近气象站长期的历年最大风速及与风电项目内测风塔同期的逐日最大风速资料, 对结果进行修正。以实测到的大风速段内的最大阵风系数, 推算风电场不同高度50年一遇的极大风速。
1 5 d最大10 min平均风速取样和50年一遇最大风速估算目前在风电项目开发中, 主要以10 min平均风速和10 min期间的3 s极值风速记录实测风速; 50年一遇最大风速通常指10 min平均风速, 50年一遇极大风速通常指3 s平均风速。如何从实测的风速母体中选取适合的子样, 用于估算50年一遇最大风速, 是决定估算结果可信度重要一步。理论上的取样方法, 一方面要能包含尽可能多的最大风速信息, 另一方面要排除影响最大风速主要信息的无效或干扰样本。
1.1 主要的极值取样法在极值理论中, 从母体风速序列中选取极值子体的方法主要有等时段法和跨阈法两种。
《全国风能资源评价技术规定》中, 取历年最大风速资料为样本, 采用极值Ⅰ型概率分布, 用改进的矩法估算分布函数的参数, 进而估算出50年一遇的最大风速。这种方法在国际上用得较多, 英、美、加、日等国的估算方法与其基本相一致[5-6], 在统计学、天气学上逻辑合理, 大量实践表明这是一种可信赖的方法。但常常因所能获得的样本容量太小, 而影响其准确性和可靠性。
在广义跨阈法[7]中, 取风速大于某一极限的样本。这种取样法在机械、电子设计中, 已经取得成功。但在用于最大风速估算时, 风速极限阈值难以确定; 各样本在时间分布上差别较大; 一年内风速大于某一极限的样本数有变化; 在季风气候区, 一年内风速大于某一极限值的风速, 可能会集中出现在某一两个季节内。
Rijkoort-Weibull分布法[8]中, 阈的初始值取风速大于2 m/s的样本, 然后分析风暴尺度并将风暴尺度外推, 再取更大的阈值来选取样本。这种取样法从2 m/s开始迭代, 能有效减少低风速对极值风速信息干扰, 也适合计算机处理资料特点, 在一些国家中已推广应用。从气象学角度来看, 风暴尺度外推过程中阈值选取较困难, 阈值偏小不能排除影响天气系统信号的无效样本, 而阈值偏大又会过滤掉有价值的天气系统信号, 且一年中风速大于阈值的概率同样会有变化。
另外, 还有月最大风速、日最大风速、60次或18次观测中的最大风速等取样法, 其普遍不足是不能很好反映当地天气系统变化的信息。
1.2 5 d最大10 min平均风速取样法我国风电场风资源评价要求有连续1年的场内实测风数据, 对此测风序列选取各实测高度上的5 d最大10 min平均风速样本, 用于估算风电场不同高度上50年一遇的最大风速, 简便易行。
在我国传统历法和物候中是以5 d为“候”, 这种候的概念反映了我国主要的物候变化规律。以5 d最大10 min平均风速取样, 可简单、完整地在1年的实测风速数据中取样, 也易于将估算期间整数化(如50年为3650个5 d), 便于计算。
由自然风平均功率谱密度PERIOD模型[9]可知, 自然风能量分布有年、4~5 d, 1 d, 1 min 4种主峰和1 h的低谷, 其中低频能量以4~5 d为周期, 符合实际大气系统的移动周期; 高频能量以1 min为周期, 正是实际脉动风周期, 并且高频谱峰能量取决于平均风速。
在求取平均风速或考察风资源总体状况时, 取10 min时距[10]是在风功率谱密度较小的周期, 这符合人们的习惯思维, 也在实践中取得了良好效果。但当考察最大风速的变化时, 应选取风功率谱密度最大的周期, 会更合理、可靠。
由罗斯贝波理论和自然天气周期概念, 天气系统对一地的影响大约有7~10 d的变化周期, 但在不同的气候区域, 又不尽相同。考虑到中小尺度天气系统的影响, 并且一次天气过程中可能会出现两个风速较大的时段, 以5 d最大10 min平均风速取样, 既能较全面地反映出较大风速的变化, 也在一定程度上能屏蔽掉无效的或有干扰的样本。
当风速增大时, 一地的垂直风切变会明显减小。据一些已开发建设的风电项目中实测风资料的统计分析, 在30 m高度以上, 当风速大于22 m/s时垂直风切变会很小, 并且多次出现50 m或60 m高度以上的负垂直风切变。这种垂直风切变随风速、高度的变化[11-12], 使得从单一的10 m高度50年一遇最大风速, 推求风电场轮毂高度处的50年一遇最大风速困难较多。
使用5 d最大10 min平均风速取样法, 能同时估算不同高度上的50年一遇最大风速, 进而较准确地推算出实际轮毂高度处的50年一遇最大风速。
在我国有些风资源较丰富的地区, 低层和高层(约30 m以上)平均风速日变化呈明显的反相变动:低层风速昼间大夜间小, 而高层风速昼间小夜间大。这主要是由于动量下传作用、地表热力性质的差异所致。使用5 d最大10 min平均风速取样法, 不须再顾虑这些地区中不同高度上风速近反相的日变化。
1.3 以5 d最大风速估算50年一遇最大风速5 d最大风速不是严格的随机过程, 样本概率之间不能严格地满足泊松分布, 这主要是由于影响当地天气的系统变化所致。而对于1年以上的风速变化来说, 5 d最大风速仍可认为是拟平稳随机过程[13], 可以适用极值Ⅰ型概率分布。
我国风电场内的实测风数据要求有1年序列, 一个实测的高度上正好可以取得73个5 d最大风速样本。以此73个样本, 用极值Ⅰ型概率分布和修正的矩参数估算法, 便可估算该高度上的50年一遇最大风速:
|
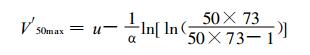
(1) |
式(1)中, u为极值Ⅰ型概率分布位置参数即分布的众值, α为分布的尺度参数。
|
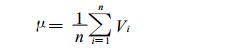
(2) |
|
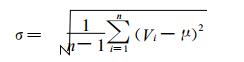
(3) |
|
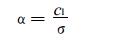
(4) |
|
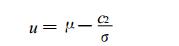
(5) |
式(2)和(3)中, Vi为1年内73个5 d最大10 min平均风速样本序列(n=73);式(4)和(5)中, c1和c2是用修正的矩法估算参数的; 当n=73时, 由《全国风能资源评价技术规定》中附表, 以内插法查得: c1=1.187907, c2=0.555403。
1年实测风序列中5 d最大10 min平均风速, 主要反映天气系统变化在一年内对当地风速的影响, 尚需考虑最大风速的年际变化。对此, 可以用邻近气象站长期数据的估算结果给予订正:①以邻近气象站的长期数据, 依照《全国风能资源评价技术规定》估算出该气象站10 m高度上50年一遇最大风速Vm1; ②以与风电场实测风同期的该气象站逐日最大风速, 使用5 d最大风速取样法估算出该气象站10 m高度上50年一遇最大风速Vm2; ③以Vm1与Vm2的差, 订正风电场内10 m高度上50年一遇最大风速; ④以订正后的风电场内10 m高度50年一遇最大风速和5 d最大风速取样法估算的风电场内各高度V′50max相应于10 m高度的垂直风切变, 估算出风电场各高度上50年一遇最大风速。
2 阵风系数变化对50年一遇极大风速的影响在国际风电机组设计标准[1]中, 以统计平均阵风系数1.4, 由10 min平均风速来推算50年一遇极大风速, 主要是为了便于风电机组疲劳载荷的测算。现在我国风能资源评估中也多用这样的阵风系数, 由50年一遇最大风速推算极大风速, 从实践情况来看不够准确和合理。
在我国北方的多数地区, 平均阵风系数都接近于1.4, 但最大阵风系数随风速的增大会明显减小, 且这种减小趋势随高度的增加会更明显。另外, 我国沿海一带在受台风或热带风暴影响时, 风场内的阵风系数虽然会随高度的增加而减小, 但各个高度上往往还会出现阵风系数大于1.4的情况。
从实际需要出发, 以实测到的较大风速段的最大阵风系数, 由前述估算的50年一遇最大风速推算极大风速, 应该更为合理、可靠。
3 乌兰伊力更风电场50年一遇最大和极大风速估算 3.1 资料使用国家第5期特许权内蒙古巴彦淖尔市乌兰伊力更风电场300 MW项目(以下简称乌兰伊力更风电场)内9010#测风塔(70 m)2006年6月5日00:00(北京时, 下同)—2007年6月4日23:50的实测风数据, 测风塔上70 m, 60 m, 40 m, 30 m, 10 m高度各安装有一风速仪, 70 m, 10 m高度各安装有一风向仪, 其所记录的风向、风速数据均完整、合理。9010#测风塔位于乌兰伊力更风电场工程项目的中间位置, 海拔高度为1338 m, 能较好地代表整个项目的风资源状况。
风电场邻近的长期观测气象站为乌拉特中旗气象站, 属国家一级气象站, 位于乌拉特中旗政府所在地海流图镇, 距国家特许权300 MW项目风电场约60 km。气象站观测场海拔高度为1288 m, 风速仪距地面高10.5 m。乌拉特中旗气象站累年观测到的最大风速为1979年出现的26.0 m/s。
由于海流图镇和乌兰伊力更风电场地形地势差别, 两地同期风速实测数据相关性较差, 不仅给长期风电场风资源平均状况评估带来困难, 而且用传统相关分析方法估算风电场内50年一遇最大风速和极大风速也难以实施。
3.2 乌兰伊力更风电场内各高度50年一遇最大风速估算由乌拉特中旗气象站1975 —2005年的逐年最大风速, 依《全国风能资源评价技术规定》 Ⅰ型极值概率分布估算方法, 取c1=1.115598, c2=0.537044, 估算乌拉特气象站10 m高度50年一遇最大风速Vm1=28.61 m/s。
由乌拉特中旗气象站2006年6月5日—2007年6月4日逐日最大风速, 以5 d最大10 min平均风速取样法, 参照《全国风能资源评价技术规定》中修正的矩法估算参数, 并取c1=1.187907, c2=0.555403, 用极值Ⅰ型概率分布估算乌拉特中旗气象站10 m高度50年一遇最大风速:Vm2=25.05 m/s。可得Vm1-Vm2=3.56 m/s。
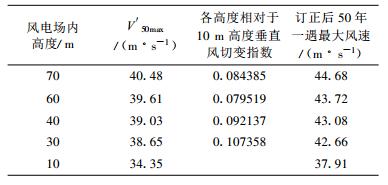
由乌兰伊力更风电场9010#测风塔2006年6月5日00:00—2007年6月4日23:50的实测风数据, 以5 d最大10 min平均风速取样法, 参照《全国风能资源评价技术规定》中修正的矩法估算参数, 取c1=1.187907, c2=0.555403, 用极值Ⅰ型估算乌兰伊力更风电场各高度50年一遇最大风速V′50max, 并用Vm1与Vm2的差3.56 m/s订正风电场10 m高度50年一遇最大风速, 再由风电场各高度V′50max相应于10 m高度的垂直风切变, 估算出风电场各高度50年一遇最大风速(表 1)。
|
表 1 5 d最大风速取样法估算的风电场内各高度50年一遇最大风速 Table 1 Sampling maximum wind speed of 5 days, estimating the extreme 10-minute average wind speed with a recurrence of 50 years at different height of wind farm |
3.3 5 d最大10 min平均风速取样法估算方法的检验
5 d最大10 min平均风速样本, 是否服从于Ⅰ型极值概率分布, 或者是否适合以Ⅰ型极值概率分布估算长期的最大风速变化, 通常可以用拟合标准差、拟合相对偏差、柯尔莫哥洛夫拟合度和变异系数4个拟合优良性指标[14]给予检验。
4个拟合优良性指标从不同的角度, 考察某概率分布对样本的拟合优良性, 指标越小则均表示样本总体越服从该概率分布, 也即适合以该概率分布估算长期样本的变化。
以4个拟合优良性指标, 对乌拉特中旗气象站5 d最大10 min平均风速取样法估算方法优良性检验:拟合标准差为0.478028;拟合相对偏差为0.028462;柯莫哥洛夫拟合度为0.078909;变异系数为0.052107。
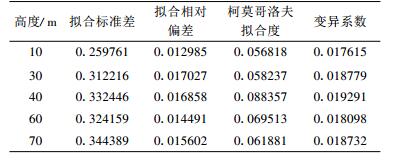
以4个拟合优良性指标, 检验乌兰伊力更风电场5 d最大10 min平均风速取样法估算结果优良性(表 2)。
|
|
表 2 乌兰伊力更风电场5 d最大风速取样法估算方法优良性检验 Table 2 The accuracy test of the estimating method of 5 days maximum wind speed sampling at Wulanyiligeng wind farm |
参考其他的一些最大风速估算的拟合效果(略)。相比之下, 表 2中的4种指标均明显较小。因此认为, 对1年的10 min平均风速母体以5 d最大10 min平均风速取样后, 使用Ⅰ型极值概率分布估算50年一遇最大风速是适合的。
3.4 乌兰伊力更风电场50年一遇极大风速的估算乌兰伊力更风电场9010#测风塔2006年6月5日00:00—2007年6月4日23:50实测到的最大风速和极大风速(表 3)。
|
|
表 3 2007年3月30日9010#测风塔实测到的最大风速和极大风速(单位: m·s-1) Table 3 The measured maximum 10-minute and 3-second wind speed at 9010# mast on March 30, 2007(unit : m·s-1) |
由表 3可见, 乌兰伊力更风电场内实测到的最大风速和极大风速不一定同时发生, 且高度不同发生的时间也有差别。
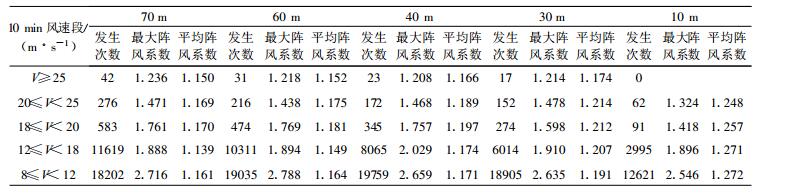
以每个10 min内最大3 s风速和该10 min平均风速比值, 表示当时的阵风系数。由表 4可见, 乌兰伊力更风电场实测最大阵风系数随风速的增大而减小, 且这种减小趋势随高度的增加更明显。
|
|
表 4 9010#测风塔实测阵风系数随风速和高度的变化 Table 4 The measured gust coefficient at 9010# mast varying with the wind speed and the height |
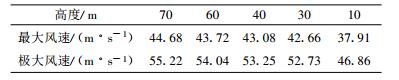
对表 1中订正后各高度50年一遇最大风速, 以实测10 min风速≥25 m/s的最大阵风系数为1.236, 推算乌兰伊力更风电场各高度50年一遇极大风速(表 5)。
|
|
表 5 乌兰伊力更风电场各高度50年一遇最大风速和极大风速 Table 5 The extreme 10-minute and 3-second average wind speed with a recurrence of 50 years at different height of Wulanyiligeng wind farm |
4 小结
在风电场内实测风资料相对较少的情况下, 用5 d最大10 min平均风速取样法估算场内各高度的50年一遇最大风速简便易行, 通过有长期观测资料的邻近气象站同期估算结果的订正, 再以实测到的极大风速段上最大阵风系数, 推算风电场内各高度50年一遇极大风速, 通过比较《全国风能资源评价技术规定》等方法的估算结果, 可获得能满足风电项目建设需要的、可信的估算结果。
经初步的试用, 在我国北方风电项目开发中, 5 d最大10 min平均风速取样法基本能够估算出比较可信的轮毂高度50年一遇最大风速。但由于取样母体资料是1年实测风资料, 其长期气候的代表性需要利用气象站资料进行修正, 这种方法的适用性还有待于进一步的验证和讨论。
致谢 中国国电龙源电力集团公司和内蒙古自治区乌拉特中旗改革和发展局在此项研究探讨的资料收集和现场踏勘中给予作者很大的帮助和支持, 特此致谢。
参考文献
| [1] | International Electrotechnical Commission. International Standard IEC61400-1:2005. 2005. |
| [2] | 全国风能资源评价技术规定.http://www.windpower.org.cn/news/links/js_2005_0513_2.htm. |
| [3] | 杨振斌, 薛桁, 桑建国. 复杂地形风能资源评估研究初探. 太阳能学报, 2004, 25, (6): 744–749. |
| [4] | 李鸿秀, 任鹏, 朱瑞兆.关于风能资源评估中最大风速的探讨.第四届亚洲风能大会暨国际风能设备展览会会议论文, 2007. |
| [5] | 林凤羽. 输电线路的风荷载. 电网技术, 1993, (6): 34–38. |
| [6] | Van den Brink H W, Kormen G P, Opsteegh J D. Statistics of Extreme Synoptic-scale Wind Speeds in Ensemble Simulations of Current and Future Climate. Royal Netherlands Meteorological Institute. www.knmi.nl/publications/fulltexts/pap_brink200302.pdf. |
| [7] | 段忠东, 欧进萍, 周道成. 极值风速的最优概率模型. 土木工程学报, 2002, 35, (5): 11–16. |
| [8] | Smits Ilia. Estimation of Extreme Return Levels of Wind Speed: A Modification of Rijkoort-Weibull Model.http://www.knmi.nl/samenw/hydra/documents/index.html, June 6, 2001. |
| [9] | 贺德馨. 风工程与工业空气动力学. 北京: 国防工业出版社, 2004. |
| [10] | 陈正洪, 向玉春, 杨宏青. 深圳湾公路大桥设计风速的推算. 应用气象学报, 2004, 15, (2): 226–233. |
| [11] | 薛桁, 朱瑞兆. 我国北部草原地区近地层平均风特性分析. 太阳能学报, 1992, 13, (3): 232–238. |
| [12] | 包能胜, 刘军峰, 倪维斗, 叶枝全. 新疆达坂城风电场风能资源特性分析. 太阳能学报, 2006, 27, (11): 1073–1077. |
| [13] | 赵林, 葛耀君, 项海帆. 极值风速拟合优化策略. 同济大学学报, 2003, 31, (4): 383–388. |
| [14] | 陈朝晖, 管前乾. 基于短期资料的重庆风速极值渐进分布分析. 重庆大学学报, 2006, 29, (12): 88–92. |