2. 中国科学院南海海洋研究所热带海洋环境动力学重点实验室, 广州 510301;
3. 广州中心气象台, 广州 510080
2. LED, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301;
3. Guangzhou Central Meteorological Observatory, Guangzhou 510080
自从Morlet在分析地震波高频成分时引进小波变换以来, 由于它在时间域和频率域上同时具有良好的局部性及数学意义上严格的突变点诊断能力, 小波变换在自然科学和技术科学领域中获得广泛应用, 成为信噪分离、图像处理、语言分析及模型识别等领域中的一种强有力的数学工具。例如, 用于研究湍流中的相干结构[1]、海洋中的波耗散[2]、大气中的冷锋[3]、热带对流[4]、ENSO[5]及英格兰中部温度变化[6]。Torrence等[7]研究了小波变换和窗口Fourier变换的比较、小波母函数的选择、时间序列的有限长度引起的边缘效应 (即影响域) 及显著性检验等问题, 将小波变换结果置于更可信的基础上, 从而使小波变换得到更广泛的应用。小波变换是大气科学研究中常用的分析方法之一, 也是气候变化研究及预测的有力工具[8-12]。另外, 小波变换与其他方法相结合的新应用也值得关注[13-16]。但在实际应用中发现存在两个问题:①对墨西哥帽小波母函数, Torrence等[7]给出的影响域范围较小, 可能会给出错误的、受边界外未知值引起的低频变化; ②用其给出的离散化计算公式计算的小波系数值在高频部分较大, 会产生虚假的高频振荡。上述两个问题对大气科学中时间序列的分析会产生不利后果:前者会影响到年代际变化的正确判断, 后者会产生虚假的准两年周期变化。本文将分析探讨这两个问题, 并试图给出解决问题的方案, 以促进小波分析技术的正确应用。从小波变换的定义着手, 首先导出正、余弦函数的墨西哥帽小波变换的解析式, 然后探讨墨西哥帽小波变换的影响域和能消除高频失真的小波系数离散化计算方案, 最后以实例验证了本文提出的新小波系数计算方案的合理性。
1 小波变换的定义及物理意义 1.1 小波变换的定义本文选用的小波母函数为墨西哥帽 (Mexican Hat) 函数
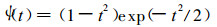
|
(1) |
它是高斯函数exp (-t2/2) 的二阶导数的负值。由ψ(t) 导出的小波函数为
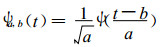
|
(2) |
对时间函数f(t), 定义其小波变换的小波系数Wf [17]和整体小波功率谱WSf分别为

|
(3) |
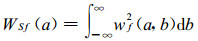
|
(4) |
式 (2)~(4) 中, a, b为实数, a为伸缩系数且a>0, 也叫做小波尺度。从式 (2) 可知, a越大, 小波函数ψa, b(t) 的支集越大, 最大值越小。b为平移因子, 反映小波变换对时间函数f(t) 的关注点。
式 (3) 为小波系数的定义式, 它反映出信号在时间局部区域上的频率特征, 而传统的Fourier分析只能反映信号的整体特征。式 (4) 反映信号在时间域的整体特征, 类似于功率谱分析, 利用它可以确定一个时间序列中存在的主要周期。
1.2 正、余弦函数的墨西哥帽小波变换众所周知, 任意函数都可以表示为不同频率、不同振幅简谐波的线性叠加。所以, 通过分析正、余弦函数的小波变换, 可以了解小波变换的物理意义。
根据小波变换的定义, 对墨西哥帽小波母函数, 可以解析地求出振幅为A、频率为ω=2π/T(T为周期) 的函数f (t)=Asin (ωt) 或Acos (ωt) 的小波变换:
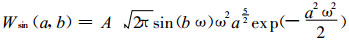
|
(5) |
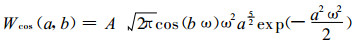
|
(6) |
可见, 小波系数与平移因子b的关系比较简单, 仅继承了原来的正、余弦函数形式且为一个独立的因子, 而频率或周期与小波尺度a的关系比较复杂。为统一研究正、余弦函数周期与小波尺度a的关系, 令sin (bω)=1, cos (bω)=1并令
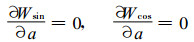
|
则小波变换的极值为:
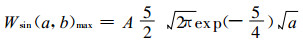
|
(7) |
同时可以导出极值点处小波尺度a和振动周期T的关系为:
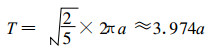
|
(8) |
式 (5)、(6) 给出了正、余弦函数小波系数的解析表达式, 它的正值、负值、零值和极值都有很好的物理意义:正值表示该小波尺度对应的振荡处于正异常位相; 负值表示该小波尺度对应的振荡处于负异常位相; 零值表示处于正、负异常位相的转换点; 小波系数极值点对应的振荡处于极值附近。式 (8) 给出了振荡周期和小波尺度的关系, 可以作为分析时间序列蕴含的振荡周期的基础。式 (7) 表明:小波系数极值的大小不仅和振幅成正比, 还和周期或小波尺度 (二者呈线性关系) 的平方根成正比。
对于有限长的正、余弦函数型时间序列, 如果时间域刚好覆盖若干个周期, 则可以求出时间平均的整体小波功率谱WSf的解析式:
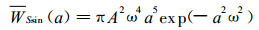
|
(9) |
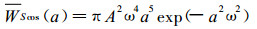
|
(10) |
按照小波变换的定义, 需要无限长的时间序列, 这在实际应用中是不可能的, 因为任何观测都是在有限长的时间段[1, N]上进行的。但由式 (1) 和 (2) 可知, 墨西哥帽小波函数是关于t=b对称的, 且在t=b处取得最大值1/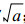
距b点多远才算“足够远”?为了便于讨论, 以及和文献[7]中结果对比, 定义小波函数的有效定义域为这样一个区域:区域以外的小波函数的绝对值都小于其最大值的1/e, 且区域以外的小波函数值迅速趋近于零。
对墨西哥帽小波母函数, 令x=(t-b)/a, 其小波函数可以写成
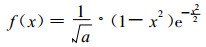
|
(11) |
可见, f(x) 的最大值为1/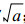
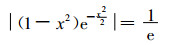
|
(12) |
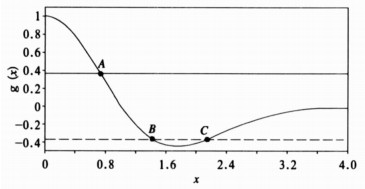
式 (12) 左边绝对值内的函数g(x)=(1-x2)· e-x2/2为偶函数, 所以可以仅讨论g(x) 在x>0时的解。图 1给出了g(x) 在x>0时的分布。可见, 函数g(x) 并非单调递减趋近于零, 而是在自变量从0到

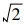
|
|
| 图 1. 函数g(x)=(1-x2)· e-x2/2在x>0时的分布 (实、虚直线分别表示1/e, -1/e) Fig 1. The distribution of function g(x)=(1-x2)·e-x2/2 for x > 0(the solid and dashed lines are for the value of 1/e and-1/e, respectively) | |
从小波函数有效定义域的定义和图 1可以看出, 小波函数有效定义域的物理意义表现为两方面:其一, 小波函数有效定义域以外的小波函数值都相对较小, 其对应的时间序列值对b点小波系数值的贡献较小, 可以忽略不计; 其二, 小波函数有效定义域以内的时间序列值对小波系数值都有较大贡献, 如果平移点b处、尺度为a的小波函数的有效定义域[b-2.12a, b+2.12a]不能完全包含在时间序列范围[1, N]内, 则b点的小波系数值就会受到时间序列边界外未知值的影响。
从小波函数有效定义域的物理意义可知, 墨西哥帽小波变换的影响域为2.12a。而文献[7]给出的小波变换影响域为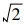
小波尺度a的最小值可以取趋于零的很小正数。但小波尺度a的最大值如何选取?在前面讨论影响域时, 已经知道左、右两边的影响域皆为2.12a, 对于长度为N的时间序列, 最大小波尺度出现在左、右两边的影响域相接时, 从而可以确定小波尺度a的最大取值应为N/4.24。因此有实际意义的小波尺度a的取值范围为 (0, N/4.24]。
2.2 小波变换的计算方案结合文献[7]中的式 (2) 和式 (8), 并令取样时间间隔为1个时间单位, 可以得到文献[7]中任意距平时间序列f(i) (i=1, …, N) 的墨西哥帽小波变换的小波系数计算公式 (对于实形小波母函数, 小波函数的共轭等于它本身):
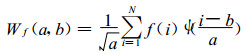
|
(13) |
当小波尺度a小到一定程度时 (如a<0.471), 根据小波函数的有效定义域, 仅有平移点b处的时间序列值影响b点的小波系数值, 式 (13) 计算的Wf(a, b)≈f(b) /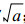
由于在气候分析中高频的对流层准两年振荡在许多气象场中显著存在[18], 因此, 只有使用正确的分析方法, 才能分清高频的准两年振荡是否为气象要素真正的固有周期, 而不是由分析工具产生的虚假周期, 从而认清事物的本质特征, 使分析的结论更可靠。
分析认为产生这种虚假高频周期的原因是文献[7]中对积分形式定义的小波变换式 (3) 作离散化处理时没有考虑小波函数的特点所导致的。从式 (2) 可知, t=b且小波尺度a→0时, 小波函数→∞, 也就是说, 式 (3) 中的被积函数有奇异性。文献[7]中的小波系数计算方案 (即式 (13)) 没有考虑到被积函数的奇异性, 仅按累加求和来替代积分。
这里给出一种新的小波系数计算方案, 该方案的主要思路是当小波尺度较小时, 通过提高分辨率来体现小波函数有效定义域大小的区别。对较小的小波尺度, 对应小波函数的有效定义域非常小, 以至于相邻点的时间序列值对其小波系数值的贡献很小。小波尺度越小, 对应小波函数的有效定义域越小, 而式 (13) 并没有反映出这种小波函数的有效定义域大小的区别。小波函数是解析的, 可以在任意分辨率上求值; 而时间序列也可以通过立方样条插值来提高其分辨率。具体做法是, 当小波尺度a≥1时, 令新网格的分辨率为1(即和原时间序列分辨率相同); 当小波尺度a<1时, 令新网格的分辨率等于小波尺度a。应注意的一个重要问题是, 平移点b处的小波函数值最大, 一定要保证平移点b在新网格上。所以, 对每一个小波尺度a和平移点b, 都通过产生新的、高分辨率的网格来计算其小波系数。对式 (3) 的积分采取如下的新计算方案:
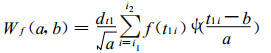
|
(14) |
其中, dt1为新网格的分辨率, 当a≥1时, 令dt1=1;当a<1时, 令dt1=a。i1=(1-b) /dt1, i2=(m-b) /dt1。t1i=b+i ×dt1, f(t1i) 由原时间序列值作三次样条内插得到。显然, 当小波尺度a≥1时, dt1=1, t1i=i, 式 (14) 和式 (13) 完全相同。但小波尺度很小时, 式 (14) 表明Wf (a, b)∝f(b)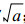
图 2给出了小波函数有效定义域大小的差异和新计算方案网格设计。为了反映小波尺度较小时的局部特征, 仅画出3个相邻时刻的序列值。从图 2a可见, 两个小的小波尺度a=0.47和a=0.16对应的小波函数的有效定义域半宽都小于1, 小波函数的有效定义域大小的差别非常明显。a=0.16的小波函数的有效定义域非常小地局限于平移点b=i附近, 但小波函数最大值较大; a=0.47的小波函数的有效定义域也局限于平移点b=i附近, 但较宽, 最大值相对较小。a=0.16时的小波函数的有效定义域范围要比a=0.47时的小很多。用式 (13) 计算平移点b=i处的小波系数时, 可以用图 2a中i处的值来近似。a=0.47和a=0.16对应的b=i处的小波系数分别为1.5和2.5。用式 (14) 计算b=i处的小波系数, 可以按图 2b中给出的高分辨率网格 (对应到小波尺度a=0.47) 积分来近似, 小波系数值为0.57;类似地, 可以画出小波尺度a=0.16对应的高分辨率网格 (图略), 小波系数值为0.08。显著的数值差异说明两个问题:第一, 两种计算小波系数公式中, 两种小波尺度对应的小波系数的相对大小发生了变化:用式 (13) 计算小波系数时, 小的小波尺度对应的小波系数值大; 而用式 (14) 计算小波系数时, 小的小波尺度对应的小波系数值小。这与前面定性分析时给出的“用式 (13) 计算出的小波系数会产生虚假的显著高频周期”是一致的; 第二, 对应于小波尺度a=0.47, 两种计算方案给出的小波系数相差近2.5倍, 误差明显。小波尺度a=0.47对应的周期为1.87, 对年序列而言, 就是准两年周期。
|
|
| 图 2. 墨西哥帽小波函数有效定义域及新计算方案网格示意图 (a) 小波尺度a=0.47(实线) 和a=0.16(虚线) 所对应的小波函数 (浅色水平线对应到这两种小波尺度上的有效定义域) 及3个相邻时间的距平序列 (柱状), (b) 小波尺度a=0.47所对应的小波函数 (实线) 及新的高分辨率网格 (竖虚线) Fig 2. Schematic diagram of effective domain of Mexican wavelet function and new computing scheme (a) wavelet functions for wavelet scale a=0.47(solid line) and a=0.16(dashed line) (light horizontal lines stand for the effective domains for these wavelet scales) and anomalous series of 3 sequential time (bar), (b) wavelet function for wavelet scale a=0.47(solid line) and new high reso lution grid (vertical dashed line) | |
3 个例分析
为了说明文献[7]中的小波变换离散化的计算方案存在产生虚假高频振荡的问题和本文提出的新计算方案的合理性, 用正弦函数及Niño3.4指数 (来自于CPC, http://www.cdc.noaa.gov/ClimateIndices/) 的小波变换加以验证。
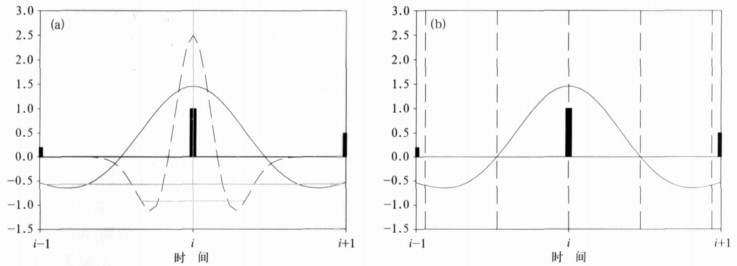
图 3为不同方案计算的时间序列f(t)=sin (2πt/4) (t=0, …, 40) 的平均整体小波功率谱。可见, 用本文提出的小波变换新计算方案和解析解式 (9) 给出的图形非常一致, 在小波尺度a<0.5时二者基本重合, 且在a趋近于零时, 平均整体小波功率谱趋近于零; 在a=1(对应的周期约等于4) 附近时, 二者虽有较小的差异, 但有共同的递增和递减区间及极值点位置, 即定性分析结果是完全一致的。产生上述较小数值差异的原因在于, 式 (9) 给出的解析结果相当于计算小波系数和平均整体小波功率谱时的积分步长是无限小, 给出的计算方案只是在a较小时取较小值。从图 3还可以看出, 当周期T小于3时, 随着小波尺度的减小, 用文献[7]的计算方案计算出的小波功率谱与式 (9) 计算出的小波功率谱的差异越来越大, 且当T<2.5时, 周期愈小, 平均整体小波功率谱越来越大。即使取最小周期T=2(对应到图中竖实线) 时, 也会产生一个虚假的高频周期振荡。对其他的周期函数, 结果类似。所以, 用文献[7]的计算方案可能会产生虚假的显著高频振荡, 而本文提出的新计算方案能正确判断时间序列蕴含的高频振荡周期。
|
|
| 图 3. 时间序列f(t)=sin (2πt/4) (t=0, …, 40) 的平均整体小波功率谱 (点线、断线和实线分别为式 (9)、文献[7]计算方案和本文新计算方案的结果) Fig 3. Mean global wavelet power spectrum of time series f(t)=sin (2πt/4)(t=0, …, 40) (dotted line, dashed line and solid line stand for the results from analytic formula (9), computing scheme in reference [7] and new computing scheme in this paper) | |
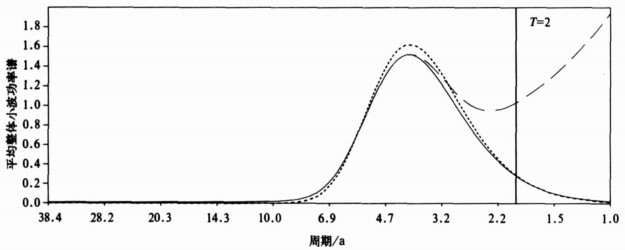
图 4给出了1951 —2007年冬季Niño3.4指数距平序列及其小波变换。图 4b为利用本文新计算方案计算的小波系数分布图。可见, 能通过α=0.1显著性水平检验的主要周期为3~4年和6年。6年左右的周期振荡显著出现在20世纪50年代至60年代初和90年代末至21世纪前期; 3~4年左右的周期振荡显著出现在20世纪60年代后期~70年代前期、80年代和90年代后期; 准两年的周期振荡仅显著出现在1974, 1984年和1999年; 12年左右的年代际变化主要出现在20世纪70年代至90年代前期, 但未通过α=0.1显著性水平检验。图 4c为利用文献[7]计算方案计算的小波系数分布图, 从影响域的大小分布可见, 文献[7]定义的影响域比本文确定的影响域小得多。从图 4c还可见, 20世纪60年代中期、70年代中前期、80年代前期、80年代末和90年代中后期均表现出显著的准两年周期振荡, 且通过α=0.05的显著性水平检验; 而在图 4b中, 除了1974, 1984年和1999年外, 这种显著的准两年振荡是不存在的。
|
|
| 图 4. 1951—2007年冬季Niño3.4指数距平序列及其小波变换 (a)1951— 2007年冬季Niño3.4指数距平序列, (b) 本文新计算方案计算的小波系数和影响域, (c) 文献[7]方案计算的小波系数和影响域 (图中两边的斜交叉线区域为影响域, 阴影分别表示通过α=0.1的显著性水平检验 (Monte-Carlo方法)) Fig 4. Time evolution of winter Niño3.4 index from 1951 to 2007 and wavelet transform (a) anomalous series of winter Niño3.4 index from 1951 to 2007, (b) wavelet coefficient computed by new computing scheme and COI in this paper, (c) wavelet coefficient computed by computing scheme and COI in reference [7] (cross-hatched regions on either end indicate the COI; shaded areas represent regions pass the test of α=0.1 level (Monte-Carlo method)) | |
从以上分析可知, 本文提出的小波系数新计算方案和文献[7]给出的计算方案差异主要体现在小波系数的高频部分和影响域大小。文献[7]给出的计算方案会产生虚假的显著高频振荡, 且由于文献[7]中给出的影响域较小, 可能会给出由于边界效应引起的低频变化中心表面处于所确定的影响域之外, 而实际上处于影响域之内的问题, 而这种问题在年代际气候变化研究中尤其重要。
图 5给出了冬季Niño3.4指数的平均整体小波功率谱。可见, 冬季Niño3.4指数存在准12年的年代际变化和准4年的年际变化; 文献[7]计算方案计算出的主要振荡周期与本文新计算方案计算出的主要振荡周期在低频部分完全一致, 而在高频部分具有明显的差异:用文献[7]计算方案计算出的平均整体小波功率谱在2年处有一个明显的峰值, 即出现虚假的准两年振荡, 而用本文提出的新计算方案不会出现这种虚假的准两年周期。
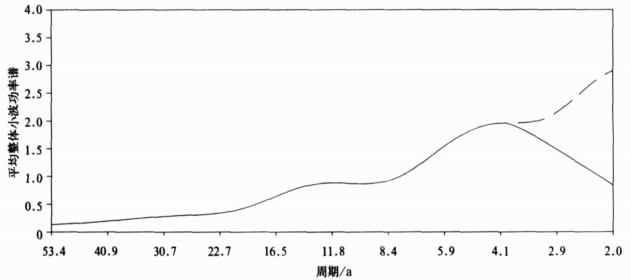
|
|
| 图 5. 1951—2007年冬季Niño3.4指数的平均整体小波功率谱 (实线为本文新计算方案, 虚线为文献[7]计算方案) Fig 5. Mean global wavelet power spectrum of winter Niño3.4 index from 1951 to 2007 (solid line is from new computing scheme in this paper and dashed line is from computing scheme in reference [7)] | |
4 结论
本文分析了墨西哥帽小波变换的物理意义, 针对文献[7]中影响域和小波系数离散化计算方案中存在的问题进行了探讨, 得到以下结论:
1) 提出了小波函数有效定义域的概念, 并探讨了有效定义域的大小与小波尺度的关系。平移点b处、小波尺度为a的墨西哥帽小波函数的有效定义域为[b-2.12a, b+2.12a]。以墨西哥帽为母函数的小波变换的真正影响域为2.12a, 而不是文献[7]中的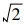
2) 充分利用小波函数速降性质和立方样条内插时间序列方法, 提出了一种新的小波系数离散化计算方案, 消除了文献[7]中离散化计算方案可能会产生虚假的显著高频周期问题, 并用正弦函数型时间序列小波变换的解析式检验了本文提出的计算方案的合理性。
3) 本文提出的新计算方案表明, 冬季Niño3.4指数存在约12年的年代际变化和准4年的年际变化, 不存在显著的准两年周期振荡。
| [1] | Farge M, Wavelet transforms and their applications to turbulence. Annu Rev Fluid Mech, 1992, 24: 395–457. DOI:10.1146/annurev.fl.24.010192.002143 |
| [2] | Meyers S D, Kelly B G, Brien J J O, An introduction to wavelet analysis in oceanography and meteorology:With application to the dispersion of Yanai waves. Mon Wea Rev, 1993, 121: 2858–2866. DOI:10.1175/1520-0493(1993)121<2858:AITWAI>2.0.CO;2 |
| [3] | Gamage N, Blumen W, Comparative analysis of lowlevel cold fronts:Wavelet, Fourier, and empirical orthogonal function decompositions. Mon Wea Rev, 1993, 121: 2867–2878. DOI:10.1175/1520-0493(1993)121<2867:CAOLLC>2.0.CO;2 |
| [4] | Weng H, Lau K M, Wavelets, period doubling, and time-frequency localization with application to organization of convection over the tropical western Pacific. J Atmos Sci, 1994, 51: 2523–2541. DOI:10.1175/1520-0469(1994)051<2523:WPDATL>2.0.CO;2 |
| [5] | Gu D, Philander S G H, Secular changes of annual and interannual variability in the Tropics during the past century. J Clim, 1995, 8: 864–876. DOI:10.1175/1520-0442(1995)008<0864:SCOAAI>2.0.CO;2 |
| [6] | Baliunas S, Frick P, Sokoloff D, et al. Time scales and trends in the central England temperature data (1659-1990):A wavelet analysis. Geophys Res Lett, 1997, 24, (11): 1351–1354. DOI:10.1029/97GL01184 |
| [7] | Torrence C, Compo G P, A practical guide to wavelet analysis. Bull Amer Meter Soc, 1998, 79, (1): 61–78. DOI:10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2 |
| [8] | 邓自旺, 尤卫红, 林振山. 子波变换在全球气候多时间尺度变化分析中的应用. 南京气象学院学报, 1997, 20, (4): 505–510. |
| [9] | 张存杰, 董安祥, 白虎志, 等. 甘肃省河东地区伏旱的小波分析. 应用气象学报, 1998, 9, (3): 291–297. |
| [10] | 尤卫红, 杞明辉, 段旭. 小波变换在短期气候预测模型研究中的应用. 高原气象, 1999, 18, (1): 39–46. |
| [11] | 纪忠萍, 谷德军, 谢炯光. 广州近百年气候变化的多时间尺度分析. 热带气象学报, 1999, 15, (1): 38–47. |
| [12] | 朱益民, 孙旭光, 陈晓颖. 小波分析在长江中下游旱涝气候预测中的应用. 解放军理工大学学报 (自然科学版), 2003, 4, (6): 90–93. |
| [13] | 李贤彬, 丁晶, 李后强. 基于子波变换序列的人工神经网络组合预测. 水利学报, 1999, (2): 1–5. |
| [14] | 戴新刚, 汪萍, 丑纪范. 准地转正压大气小波谱模式及其数值解. 自然科学进展, 2004, 14, (9): 1012–1019. |
| [15] | 赵洋, 肖华勇, 李振鹏, 等. 一种基于小波分析理论的灰色预测方法. 西南民族大学学报 (自然科学版), 2005, 31, (4): 498–501. |
| [16] | 全利红, 胡非, 程雪玲. 用小波系数谱方法分析湍流湿度脉动的相干结构. 大气科学, 2007, 31, (1): 57–63. |
| [17] | 李世雄, 刘家琦. 小波变换和反演数学基础. 北京: 地质出版社, 1994: 10-14. |
| [18] | 郑彬, 梁建茵. 对流层准两年周期振荡的研究进展. 热带气象学报, 2005, 21, (1): 79–86. |
 2009, 20 (1): 62-69
2009, 20 (1): 62-69

