应用气象学报  2008, 19 (6): 760-769   PDF    
引用本文
张莉, 丁一汇. 全球海气耦合模式对我国极端强降水模拟检验[J]. 应用气象学报, 2008, 19(6): 760-769.
Zhang Li, Ding Yihui. Evaluation of Extreme Heavy Precipitation in Coupled Ocean-atmosphere General Circulation Models[J]. Journal of Applied Meteorological Science, 2008, 19(6): 760-769  
全球海气耦合模式对我国极端强降水模拟检验
张莉1,2,3, 丁一汇2     
1. 中国气象科学研究院, 北京 100081;
2. 国家气候中心, 北京 100081;
3. 中国科学院研究生院, 北京 100049
2008-02-18 收到, 2008-05-28 收到修改稿.
资助项目: 科技部国际合作项目“区域气候变化的监测、模拟和影响研究”(2005DFA20940)、国家重点基础研究发展计划 (973计划)“亚印太交汇区海气相互作用及其对我国短期气候的影响”项目、“亚洲季风区水份循环和变异机制课题”(2006CB403604)、国家科技支撑计划“全球环境变化应对技术研究与示范”项目、“气候变化的检测和预估技术研究”课题 (2007BAC03A01) 和国家自然科学基金“东亚夏季风对全球气候变化的响应和不确定性研究”(40605020) 共同资助    
摘要: 以1961—1999年我国地面观测逐日降水资料作为观测基础, 初步分析了18个全球海气耦合模式对我国20世纪极端强降水的模拟能力。分析模式对不同级别降水的模拟发现, 各模式模拟的我国1~10 mm小雨日数普遍明显偏多; 10~25 mm中雨日数的模拟结果总体上也以偏多为主, 虽然部分模式能够模拟出我国南方存在的高值中心, 但位置偏北至长江中下游地区; 25~50 mm大雨日数在我国南方明显偏少, 并且大值中心的位置基本都没能模拟出来; 50 mm以上暴雨日数的模拟结果也明显偏小, 除MIROC3.2(hires) 外大部分模式在长江以南地区的结果都未超过2 d; 大部分模式不能正确模拟出我国东部地区大雨日数变化趋势的空间分布。进一步分析各模式对极端强降水的模拟发现:各模式极端强降水阈值明显低于观测; 半数左右的模式模拟出了1961—1999年西北西部极端降水增加的趋势, 个别模式趋势系数的大小与观测相当, 大部分模式对东北和长江中下游地区的模拟结果呈与观测反向的变化趋势, 没有模式能够模拟出我国东部地区存在的东北—华北与华中—长江中下游—华南存在的极端强降水日数增加-减少-增加-减少的空间分布; 大部分模式模拟的极端强降水日数标准差与观测结果比较接近, 这可能主要是由于对观测和各模式使用了同样的判定极端强降水发生的方法。总的来看, 全球海气耦合模式对我国极端强降水的模拟能力还有待进一步改进。
关键词: 全球海气耦合模式    极端强降水    模拟    检验    
Evaluation of Extreme Heavy Precipitation in Coupled Ocean-atmosphere General Circulation Models
Zhang Li1,2,3, Ding Yihui2     
1. Chinese Academy of Meteorological Sciences, Beijing 100081;
2. National Climate Center, Beijing 100081;
3. Graduate University of Chinese Academy of Sciences, Beijing 100049
Abstract: Based on the surface observation of daily precipitation from 1961 to 1999 in China, the simulation capabilities of 18 coupled ocean-atmosphere general circulation models for extreme heavy precipitation in China are evaluated.The analysis of annual rainy days with different categories precipitation in models shows that the annual rainy days with 1—10 mm daily precipitation in China are overestimated in all of the 18 models.The annual rainy days with 10—25 mm daily precipitation are also overestimated in most areas of China in most of the models and the high value center locates in South China in observation northward to the mid-low reaches of Yangtze River Basin in some models although those models are able to capture the high value centers to some extent.The annual rainy days with 25—50 mm daily precipitation are obviously underestimated especially in the southern China in the models and the locations of high value centers are missed in most of the models.The annual rainy days with daily precipitation greater than 50 mm are also obviously underestimated in all of the models, the days in the models except MIROC3.2(hires) are less than 2 days in south of the Yangtze River.And most models are not able to simulate the right spatial distribution of heavy rain trend in eastern China.The analysis of extreme heavy precipitation in models shows that the thresholds of extreme heavy precipitation are generally underestimated in all of the models; similar increase trend in west part of Northwest China to observation are obtained in about half of the models, and the trend coefficients in some individual model are close to the observation.While opposite linear trend in northeast area and mid-low reaches of the Yangtze River is produced by most of the models, and the " +-+-" spatial mode in Eastern China for the extreme heavy precipitation can not be caught hold by any model; close standard deviations of annual rainy days with extreme heavy precipitation with observation are obtained by most models, which is maybe mainly due to the same analysis method among the observation and the models.In conclusion, it is very necessary to further improve the simulating capabilities of the coupled ocean-atmosphere general circulation models for extreme heavy precipitation.
Key words: coupled ocean-atmosphere general circulation model     extreme heavy precipitation     simulation         
引言

极端强降水事件因其所引发灾害的严重性一直受到国内外研究者的关注, 尤其最近几年, 全球变暖背景下一些地区极端强降水事件也发生了一定的变化, 就我国而言, 西北西部[1-3]、长江中下游[4-5]部分地区极端强降水日数增加, 华北[1, 6]和华南[2]部分地区极端强降水日数减少, 并且部分地区的降水强度也有所变化[7]。不同于平均气候态的变化, 与极端事件有关的变化对自然和社会可能产生更为重大的影响。防灾减灾和可持续发展是21世纪世界各国面对的最重大的问题。全世界90%的自然灾害都与天气、气候和水相关, 而各种极端天气气候事件在所有气象灾害中破坏性最大。我国作为受极端气候事件影响较大的国家之一, 如何获知未来极端强降水事件的变化, 以更好地开展未来防灾减灾工作?全球海气耦合模式是当前预估极端强降水未来变化不可或缺的重要工具。而全球海气耦合模式对极端强降水的模拟能力则是把握极端强降水未来演变趋势的前提。因此, 检验和评估全球海气耦合模式对极端强降水事件的模拟能力, 不仅可以为模式的改进提供有益的参考, 对如何基于现有模式的预估结果进行未来的防灾减灾工作也将提供非常重要的信息。尽管有研究已经利用新一代的全球海气耦合模式对未来极端强降水事件进行了趋势分析[8-11], 但考虑到模拟结果的可靠性, 应该首先检验模式对极端强降水的模拟能力。虽然在检验模式对降水的模拟能力方面开展了不少工作[12-17], 同时也有研究指出极端降水模拟结果的统计量与观测更为接近[18-19], 但有关当前一代全球海气耦合模式对极端强降水模拟能力的检验方面目前仍比较欠缺, 尤其是专门针对我国的研究。

本文基于过去几十年我国地面观测逐日降水资料, 对18个全球海气耦合模式模拟我国不同级别降水、极端强降水阈值以及极端强降水事件年发生日数的长期变化趋势等方面的能力进行了综合分析。

1 资料

观测资料:国家气象信息中心提供的1961-1999年我国743个地面观测站点的逐日降水资料, 选择研究时段内无缺测的站点 (502个) 作为本研究的观测基础。

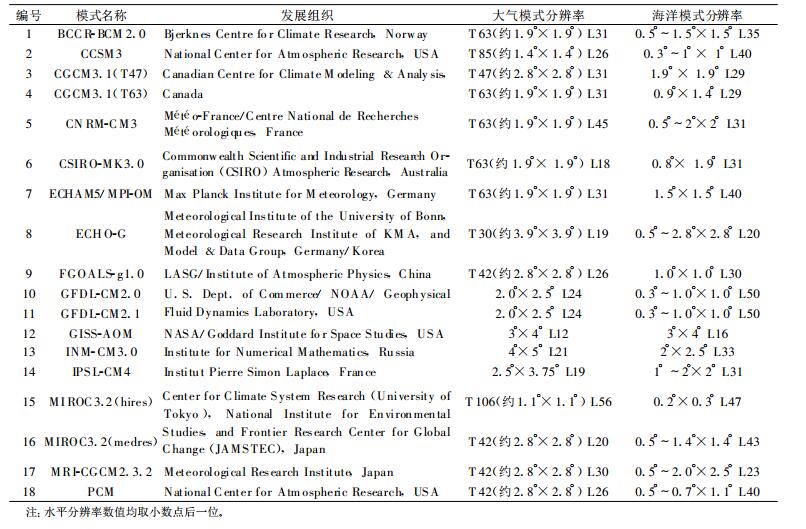
模式模拟结果:18个全球海气耦合模式模拟的1961-1999年逐日降水格点资料, 该资料从指定网站 (ftp-esg.ucllnl.org) 下载得到, 模式概况见表 1。

表 1 模式概况 Table 1 Introduction of Models

2 方法

我国将日雨量r在10 mm以下的降水称为小雨, 10 mm≤r < 25 mm为中雨, 25.0 mm≤r < 50 mm为大雨, 50 mm≤r < 100 mm为暴雨。本文首先对观测和各模式模拟的逐日降水 (r) 按照1 mm≤r < 10 mm, 10 mm≤r < 25 mm, 25.0 mm≤r < 50 mm和r≥50 mm几个等级进行了统计, 分析模式对不同级别降水的模拟能力。

考虑到我国不同区域降水的空间分布差异较大, 不能用统一的降水量值作为不同地区极端强降水的阈值, 本文使用统一的方法来计算各地的极端强降水阈值, 进而分析极端强降水的有关参数。本文定义极端强降水阈值的方法为:将1961-1999年逐年日降水量序列的第99个百分位值的多年平均值定义为极端强降水事件的阈值, 当某点某日降水量超过该点极端强降水事件的阈值时, 就称之为极端强降水事件发生[20]。

对极端强降水事件阈值的确定, 一般有非参数和参数两种确定方法。Bonsal等指出, 如果某个气象要素有n个值, 将这n个值按升序排列x 1, x 2, …, x m, …, xn, 某个值小于或等于xm的概率[21]:

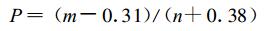
(1)

式 (1) 中, m为x m的序号, 如果有30个值, 那么第95个百分位上的值为排序后的x29 (p=94.4%) 和x30(p=97.7%) 的线性插值; n为某个气象要素值的个数。

用式 (1) 估计百分位值, 不但计算方便, 而且避免了对要素序列分布的任何假设。这种百分位值的计算方法与使用Gamma分布比较起来, 结果几乎等同[20]。

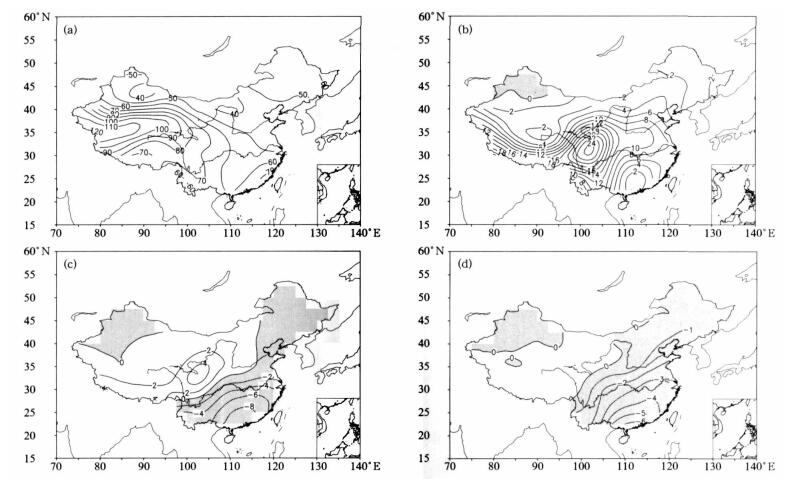
3 结果分析 3.1 模式对不同级别降水的模拟

观测分析表明 (图略), 1~10 mm小雨日数总体上南方普遍大于北方, 低值区主要集中在35°~45°N之间, 低值中心位于我国西北地区, 高值中心位于长江中上游地区。对模拟结果的分析显示 (图略), 大部分模式能够模拟出我国1~10 mm小雨日数南方普遍大于北方的形势, 但低值区和低值中心的位置稍偏北5个纬度左右, 雨日数值明显比观测大, 并且多数模式模拟的大值中心位置偏北、偏西; 就我国东部地区来看, 有少数模式CCSM3, ECHAM-MPI-OM, GFDL-CM 2.0, GFDL-CM 2.0, MIROC 3.2(hires), MIROC 3.2(medres) 在我国东部地区的模拟偏差在空间上的差别相对较小, 这可能暗示了这些模式对该地区小雨日数模拟偏差产生的原因或许存在某些共性; 总的来看, ECHAM-MPI-OM的结果更接近观测; 多模式平均表现出大部分模式模拟结果的特点, 基本上能够再现1~10 mm小雨日数的高低值空间分布, 但数值比观测偏高, 低值带和低值中心稍偏北, 高值中心偏西偏北。进一步分析多模式平均相对观测的偏差 (图 1a), 结果发现, 我国1~10 mm小雨日数的模拟结果均比观测值偏高, 高偏差中心位于西部地区的中部, 低偏差区主要位于河套地区和西北地区北部; 东部地区的偏差, 华南最大, 长江中下游和东北次之, 华北地区最小。

图 1. 多模式集合的不同级别年降水日数相对观测的偏差 (单位:d, 阴影区域为负值) (a)1~10 mm, (b)10~25 mm, (c)25~50 mm, (d)50 mm以上 Fig 1. Biases of annual rainy days with different categories precipitation between multi-model ensemble and observation (unit:d) (a)1-10 mm, (b)10-25 mm, (c)25-50 mm, (d) above 50 mm

观测分析表明 (图略), 10~25 mm中雨日数南多北少, 高值中心位于华南地区, 低值中心位于西北地区。模拟结果的分析表明 (图略), 大部分模式基本上能够模拟出中雨雨日南多北少的空间分布形势以及低值中心位于西北地区的特点, 雨日数值与观测相当或稍偏多, 个别模式能够模拟出华南地区存在的高值中心, 也有模式虽模拟出了高值中心但位置偏北, 然而多数模式在青藏高原东部存在一个虚假的大值中心, 这可能与多数模式对青藏高原地区降水模拟较差有关。各模式相对观测的偏差场显示, CGCM3.1 (T47), CGCM 3.1(T63), CSIRO-Mk 3.0, ECHO-G, IPSL-CM4在东北地区模拟的结果偏低; CGCM 3.1 (T47), CGCM 3.1(T63), CSIRO-Mk 3.0, ECHAM5-MPI-OM, FGOALS-g 1.0, GFDL-CM 2.0, GFDL-CM 2.1, GISS-AOM, INM-CM 3.0, MIROC 3.2(medres), MRI-CGCM 2.3.2, PCM在西北大部地区模拟的结果偏低; CCSM3, CGCM 3.1(T47), CGCM 3.1(T63), CNRM-CM3, CSIRO-Mk 3.0, FGOALS-g 1.0, IPSLCM4在华南地区的模拟结果偏低; 大部分模式对我国其他大部分地区的模拟结果均偏高; 就偏差幅度来看, GFDL-CM 2.0, GFDL-CM 2.1和MIROC 3.2 (hires) 的模拟结果相对更接近观测。多模式平均结果显示, 华南地区存在一个高值中心, 但位置比观测偏东, 青藏高原东部存在一个虚假的大值中心。进一步计算多模式平均相对观测的偏差 (图 1b), 高偏差中心位于我国西南地区, 高于10 d的偏差区主要分布在我国的黄淮西部向西西南方向的西南和青藏高原南侧, 华南、东北和西北都是偏差相对较小的地区。

观测分析表明 (图略), 25~50 mm大雨日数的空间分布与10~25 mm中雨日数类似, 呈南多北少型分布, 高值中心位于华南, 低值中心位于西北地区。模拟结果的分析显示 (图略), 大多数模式的结果在西北地区存在低值中心, 这与观测类似, 但在南方的结果明显偏低; 虽然半数左右的模式能够模拟出南方存在一个高值中心, 但位置基本不在华南而是普遍偏北、偏东, 并且大部分模式的结果在青藏高原东侧存在虚假的大值中心。各模式相对观测的偏差场显示, 大部分模式BCCR-BCM 2.0, CCSM3, CNRM-CM3, CSIRO-Mk 3.0, ECHO-G, GISS-AOM, FGOALS-g 1.0, GFDL-CM 2.0, GFDL-CM 2.1, IPSL-CM4, MRICGCM 2.3.2, PCM在我国东部的大部分地区均为负偏差, 其中CSIRO-Mk 3.0和ECHO-G在我国大部地区的结果偏低; 除MIROC 3.2(hires) 外, 其他所有模式在我国东部长江以南地区的模拟结果均偏低; 除ECHAM5-MPI-OM, INM-CM 3.0在东北大部结果偏高外, 其他大部分模式在东北大部地区的结果均偏低; 而大部分模式在中部和西南大部分地区的模拟结果偏高。多模式的平均结果显示, 北方的结果比南方更接近观测, 低值中心位于西北地区, 而长江以南地区的结果则明显偏低, 观测中存在华南地区的高值中心在模拟结果中偏北至长江三角洲地区, 并且青藏高原东侧存在一个虚假的大值中心。进一步计算多模式平均相对观测的偏差 (图 1c), 结果发现, 东部大部分地区和西北北部为负偏差, 东部地区的偏差大小由南向北减小, 江淮地区以南大部分地区基本都处在负偏差区, 其中华南地区的负偏差最大; 而在华北西北部、内蒙古中部、黄河中上游、西北地区南部、青藏高原的南侧和东侧等地区为正偏差, 其中正偏差中心出现在黄河上游地区。

观测分析表明 (图略), 50 mm以上暴雨主要出现在长江以南, 尤其是华南沿海地区, 呈明显的由南向北减少的分布型, 青藏高原东侧小范围内也存在一个高值中心。模拟结果的分析表明 (图略), 所有模式模拟50 mm以上的暴雨日数明显偏少, 大部分模式在我国东部地区的结果都不到2 d, 其中半数以上的模式还不到1 d。各模式结果相对观测的偏差场显示, 所有模式正负偏差的空间分布基本一致, 西北地区大部、高原东侧向东北至内蒙古中东部地区一线以东的大部地区偏低, 其他地区偏高; 单就偏差幅度来看, MIROC3.2(hires) 总体上与观测更接近, 表现出其作为高分辨率模式对我国降水模拟的优势。多模式平均结果则反映了大部分模式模拟结果的共同特征, 我国50 mm以上暴雨日数的气候平均值均不到1 d。由多模式平均结果相对观测偏差分布可知 (图 1d), 我国东部地区和西北地区北部为负偏差区, 最大偏差出现在华南沿海; 沿青藏高原东侧向东北至内蒙古中东部地区一线和沿青藏高原北缘分布的偏差零线所包围的我国西部的大部分地区为正偏差区, 但正偏差的幅度一般不到1 d。

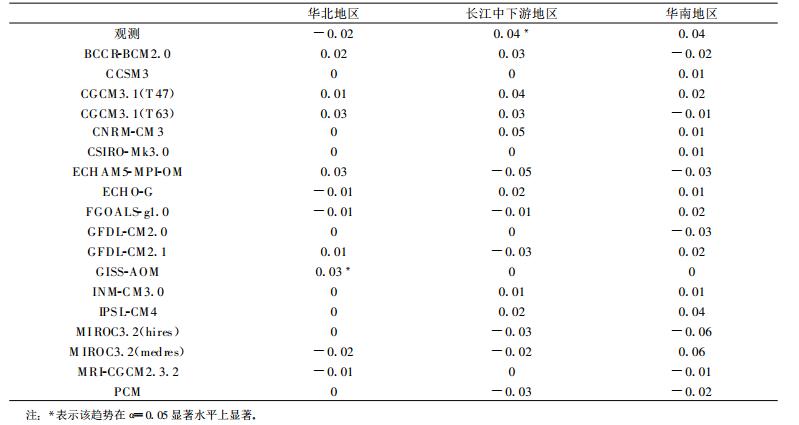
3.2 模式对我国东部地区大雨日数变化趋势的模拟

使用模式对我国东部3个地区 (华北、长江中下游和华南)25~50 mm大雨日数变化趋势进行模拟。分别计算1961-1999年观测和各模式在这3个地区区域平均的大雨日数, 进而求得相应的变化趋势, 并对趋势在0.05显著水平上进行检验 (表 2)。观测研究表明, 华北地区大雨日数在1961-1999年期间呈减少趋势, 长江中下游和华南地区则为增加趋势, 其中仅长江中下游地区的增加趋势是显著的。模拟结果显示, 18个模式中仅有4个模式ECHO-G, FGOALS-g 1.0, MIROC 3.2 (medres), MRI-CGCM 2.3.2模拟出了华北地区大雨日数的减少趋势, GISS-AOM在华北地区的结果尽管显著但与观测反向, 并且除GISS-AOM之外其他所有模式中华北地区大雨日数变化的趋势都不显著; 长江中下游地区, 18个模式中有7个模式BCCR-BCM 2.0, CGCM 3.1 (T47), CGCM 3.1(T63), CNRM-CM3, ECHO-G, INM-CM 3.0, IPSL-CM4模拟出了与观测一致的大雨日数增加的趋势, 6个模式ECHAM5-MPI-OM, FGOALS-g 1.0, GFDL-CM 2.1, MIROC 3.2(hires), MIROC 3.2(medres), PCM模拟的结果与观测趋势相反, 但所有模式的结果都不显著; 华南地区, 10个模式CCSM3, CGCM 3.1 (T47), CNRMCM3, CSIRO-Mk 3.0, ECHO-G, FGOALS-g 1.0, GFDL-CM 2.1, INM-CM 3.0, IPSL-CM4, MIROC 3.2 (medres) 得到了与观测一致的大雨日数增加的趋势, 7个模式BCCR-BCM 2.0, CGCM 3.1 (T63), ECHAM5-MPI-OM, GFDL-CM 2.0, MIROC 3.2 (hires), MRI-CGCM 2.3.2, PCM模拟的结果与观测相反, 但所有模式得到的大雨日数增加或减少的变化趋势都不显著。总的来看, ECHO-G基本上较好的抓住了这3个地区大雨日数变化趋势的信号, 不过趋势系数的大小、变化趋势的显著性以及正负趋势的分布范围与观测之间仍存在一定的差别; CGCM 3.1 (T47), CNRM-CM3, INM-CM 3.0和IPSL-CM4对长江中下游和华南地区的变化趋势有较好的把握; FGOALS-g 1.0和MIROC 3.2(medres) 则抓住了华北和华南地区大雨日数变化的方向。

表 2 我国东部3个地区1961 — 1999年观测和模拟大雨日数变化趋势 (单位:d/a) Table 2 Observed and simulated trends of annual rainy days with heavy precipitation in Eastern China from 1961 to 1999(unit:d/a)

3.3 模式对极端强降水阈值的模拟

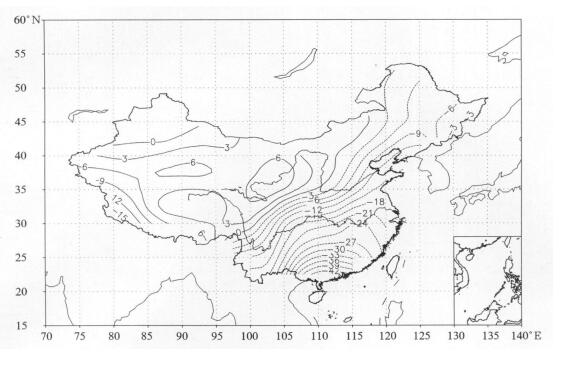
分别计算502个观测站点和各模式逐点的极端强降水阈值, 得到观测和模拟的极端强降水阈值的空间分布。观测资料的分析表明 (图略), 我国极端强降水阈值由东南沿海向西北内陆逐渐减小, 华南沿海最大, 西北内陆最小, 另外在长江中下游和青藏高原东侧还存在两个次高值中心。对模拟结果的分析发现 (图略), 我国东部黄河以南的大部分地区, 所有模式模拟的极端强降水阈值比观测偏低, 且由北向南偏低幅度增加, 华南地区偏低幅度最大; 青藏高原地区, 所有模式在青藏高原西部地区的结果一致偏高, CSIRO-Mk 3.0, ECHO-G, GISS-AOM, INMCM 3.0, IPSL-CM4, MRI-CGCM 2.3.2, PCM在青藏高原中东部的结果偏低, GFDL-CM 2.0, GFDLCM 2.1则在青藏高原中部和东南侧的结果偏低, CCSM 3, CNRM-CM 3在青藏高原东南侧小范围内的结果偏低; BCCR-BCM 2.0, CCSM 3, CGCM 3.1 (T63), CSIRO-Mk 3.0, ECHAM 5-MPI-OM模拟的西北地区极端强降水阈值与观测相对比较接近, 半数左右的模式模拟的西北地区极端强降水阈值明显偏低, 由于西北地区是降水较少的地区, 因此偏低幅度也比东部大部分地区的小; 除ECHAM5-MPIOM和MIROC 3.2(hires) 的结果在东北和华北地区偏高外, 其他模式在东北和华北大部地区的结果普遍比观测低。多模式平均的极端强降水阈值与观测进行比较可知, 多模式平均的低值中心位于西北地区, 这与观测相似; 而大值区位于江淮地区, 大值中心位于长江三角洲, 这与观测分析中的次大中心位置接近但稍偏北, 而华南存在的最大值区则没能模拟出来。多模式平均相对观测的偏差场显示 (图 2), 偏差零线沿青藏高原东南侧向东北延伸至内蒙古东部一线, 零线以东或东南部地区的模拟结果偏低, 且偏低幅度由北向南增加, 华南的偏低幅度最大; 而零线以西或西北的大部地区 (除西北北部) 极端强降水阈值比观测偏高, 高原西南侧的偏高幅度较大, 考虑到高原地区 (尤其是高原腹地) 的观测相对较少, 高原地区的结果可能存在较大的不确定性。

图 2. 多模式集合的极端强降水阈值相对观测的偏差 (单位:mm/d) Fig 2. Biases of extreme heavy precipitation threshold between multi-model ensemble and observation (unit:mm/d)

3.4 模式对年极端强降水日数变化趋势的模拟

基于我国502个站点的观测资料分析表明 (图 3), 1961-1999年我国东部地区极端强降水的变化趋势呈明显的“ +(东北)-(华北)+(长江中下游)-(华南沿海)”的分布型, 华北黄淮大部分地区、西南和华南沿海部分地区极端强降水日数有减少趋势, 其余大部分地区, 极端强降水日数有增加趋势; 趋势系数以西北西部地区最大、长江流域次之; 显著性检验结果显示, 除西北小部分地区为显著增加外, 全国大部分地区极端强降水日数的变化趋势并不显著。

图 3. 多个全球海气耦合模式模拟的年极端强降水日数变化趋势与观测对比 (单位:d·a-1) Fig 3. Multi-model simulated and observed trends of annual days for extreme heavy precipitation (unit:d·a-1)

对各模式进行同样的分析 (图 3), 从趋势系数的正负来看, BCCR-BCM 2.0, CCSM3, CGCM 3.1(T47), CGCM 3.1(T63), ECHAM5-MPI-OM, GFDL-CM 2.0, GFDL-CM 2.1, GISS, AOM, MIROC 3.2(hires), MIROC 3.2(medres) 模拟出了西北地区大部极端强降水增加的趋势, 并且个别模式在西北局部地区的趋势系数的大小与观测相当; 对东北地区而言, 除BCCR-BCM 2.0, CCSM3, CNRM-CM3, GFDL-CM 2.0, GFDL-CM 2.1, GISS-AOM, MRI-CGCM 2.3.2和PCM在东北大部地区的趋势与观测相同外, 其他模式在东北大部地区的结果与观测相反; 虽然, 长江中下游地区的极端强降水日数增加的趋势在BCCR, BCM 2.0, CGCM 3.1(T47), CGCM 3.1(T63), CNRM, CM3, CSIRO-Mk 3.0, ECHO-G, PSL-CM4, MIROC 3.2 (hires) 的模拟结果中有所反映, 但仅BCCR-BCM 2.0的模拟结果对长江中下游地区趋势系数的大值中心有所反映, 且数值大小和大值中心的位置与观测存在一定差别, 其他大部分模式的模拟结果则与观测反向; 虽然有模式抓住了华北局部地区极端强降水日数减少的趋势, 但仅INM-CM 3.0对华北大部地区的减少趋势有较好的反映; 显著性检验的结果显示 (图略), 所有这些模式模拟的我国大部地区极端强降水日数的变化趋势都不显著; 总体来看, 只有BCCR-BCM 2.0基本上模拟出了我国东部地区极端强降水变化趋势的空间分布, 但正负中心的范围和趋势系数大小与观测之间仍存在不小的差别。

3.5 模式对年极端强降水日数标准差的模拟

统计观测和各模式模拟的1961-1999年逐年极端强降水日数, 并计算该时段内的标准差。观测资料的分析表明, 除个别小范围地区外, 我国大部分地区的年极端降水日数的标准差为2 d左右, 其中长江中下游、西北北部、华北西部、东北北部以及青藏高原东部存在标准差超过2 d的大值中心, 即这些地区的极端强降水日数年际变化较大。

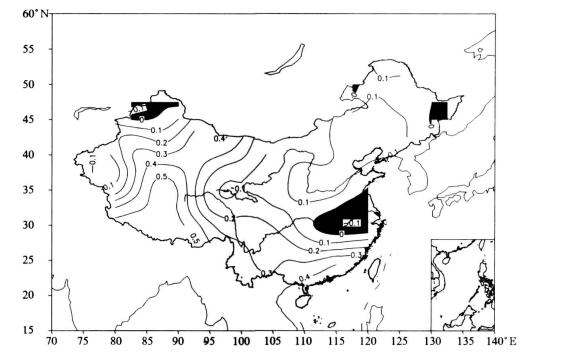
对各模式逐个格点进行分析, 发现尽管大部分模式模拟的年极端强降水日数标准差在我国都在2 d左右, 但具体数值还是存在一定的差别, 尤其是大部分模式在西北中部和华南地区的偏大比较明显; 没有模式能够较好地给出与观测类似的标准差高值中心的正确分布。多模式平均极端强降水日数的标准差相对观测的偏差场显示 (图 4), 除东北地区东部和西部边缘、西北地区北部小范围地区以及长江中下游部分地区偏小外, 其他地区的结果均偏大, 其中青藏高原和华南沿海的正偏差最大, 华北北部和东北南部、西北西部以及西北北部小范围地区正偏差相对较小。这一结果说明, 除长江中下游等地区负偏差外, 我国大部分地区的年极端强降水日数的年际变幅, 模拟结果都比实际观测要大。分析认为, 尽管模式中年极端强降水日数标准差的结果与观测比较接近, 但这一结果并不能说明模式对极端强降水年际变幅模拟能力的高低, 原因可能在于对研究时段内的观测和模拟序列采用了相同的计算极端降水阈值的方法。

图 4. 多模式集合的年极端强降水日数标准差相对观测的偏差 (单位:d) Fig 4. Biases of standard deviation of annual days for extreme heavy precipitation between multi-model ensemble and observation (unit:d)

4 小结

通过以上分析发现, 各模式模拟的我国1~10 mm小雨日数普遍明显偏多; 10~25 mm中雨日数的模拟结果总体上也以偏多为主, 虽然部分模式能够模拟出南方存在的高值中心, 但位置偏北至长江中下游地区; 25~50 mm大雨日数在南方明显偏少, 并且大值中心的位置基本都没能模拟出来; 50 mm以上暴雨日数的模拟结果也明显偏小, 除MIROC3.2(hires) 外大部分模式在长江以南地区的模拟结果都没超过2 d。这一结果与前人的研究一致[13], 说明大部分模式对降水强度的模拟能力还很不够, 尤其不能正确地模拟出高强度的降水, 这可能与模式在东亚地区模拟的大气比湿场偏低、水汽输送偏弱以及环流强度偏弱等[22]有一定关系, 但最根本的原因还需要对模式中具体的参数化方案和物理过程做进一步分析。对华北、长江中下游和华南地区大雨日数变化趋势的分析发现, 虽然每个区的变化趋势在部分模式中都有一定程度的反映, 但大部分模式却不能同时模拟出3个区的正确趋势, 也没能模拟出大雨日数变化趋势在我国东部地区的空间分布。

考虑到我国降水分布的区域差异, 对观测各台站和模式各格点降水量序列采用同样的方法计算极端强降水阈值, 即用1961-1999年逐日降水量序列第99个百分位值的多年平均值定义为极端强降水事件的阈值, 当某点某日降水量超过该点极端降水事件的阈值时, 作为极端强降水事件发生。分析发现, 各模式极端强降水阈值明显低于观测, 这与模式模拟降水量偏低有关; 半数左右的模式模拟出了1961-1999年西北西部极端降水增加的趋势, 个别模式趋势系数的大小与观测相当, 大部分模式对东北和长江中下游地区的模拟结果呈与观测反向的变化趋势, 没有模式能够模拟出我国东部地区存在的东北-华北和华中-长江中下游-华南存在的极端强降水日数增加-减少-增加-减少的空间分布, 这一点说明模式在预估极端强降水变化趋势的能力方面还有待提高, 直接使用模式预估结果对未来极端强降水的变化趋势进行判断时需要慎重; 另外, 模式对年极端强降水日数标准差模拟的结果与观测还是比较接近的, 但这一结果并不能说明模式对极端强降水年际变幅模拟能力的高低, 原因可能在于对研究时段内的观测和模拟序列采用了相同的计算极端降水阈值的方法。

总的来看, 当前全球海气耦合模式对极端强降水的模拟能力还有待大大提高, 使用模式预估结果分析极端降水的变化时需要慎重。

致谢 感谢各模式组提供的模拟结果, 感谢气候模式诊断与比较计划 (PCMDI) 收集并存储模式输出结果, 感谢JSC/CLIVAR耦合模式工作组 (WGCM) 组织模式资料分析工作; IPCC资料存储得到美国能源部科学办公室的支持; 感谢IPCC AR4 WGITSU在模式结果方面的技术支持。
参考文献
[1] 翟盘茂, 任福民, 张强. 中国降水极值变化趋势检测. 气象学报, 1999, 57, (2): 208–216.
[2] 钱维宏, 符娇兰, 张玮玮, 等. 近40年中国平均气候与极值气候变化的概述. 地球科学进展, 2007, 22, (7): 673–684.
[3] 任朝霞, 杨达源. 近40a西北干旱区极端气候变化趋势研究. 干旱区资源与环境, 2007, 21, (4): 10–13.
[4] 张天宇, 程炳岩, 刘晓冉. 近45年长江中下游地区汛期极端强降水事件分析. 气象, 2007, 33, (10): 80–87.
[5] 张文, 寿绍文, 杨金虎. 长江中下游地区汛期极端降水量的异常特征分析. 气象, 2007, 33, (3): 61–67.
[6] 马柱国, 华丽娟, 任小波. 中国近代北方极端于湿事件的演变规律. 地理学报, 2003, 58, (增刊): 69–74.
[7] 孙凤华, 杨素英, 任国玉. 东北地区降水日数、强度和持续时间的年代际变化. 应用气象学报, 2007, 18, (5): 610–618.
[8] Rasmus E, Benestad. Can we expect more extreme precipitation on the monthly time scale?. J Climate, 2006, 19: 630–637. DOI:10.1175/JCLI3656.1
[9] Gerald A Meehl, Francis Zwiers, Jenni Evans, et al. Trends in extreme weather and climate events: Issues related to modeling extremes in projections of future climate change. Bull Amer Meteor Soc, 2000, 81, (3): 427–436. DOI:10.1175/1520-0477(2000)081<0427:TIEWAC>2.3.CO;2
[10] 张勇, 许吟隆, 董文杰, 等. 中国未来极端降水事件的变化——基于气候变化预估结果的分析. 自然灾害学报, 2006, 15, (6): 228–234.
[11] 江志红, 丁裕国, 陈威霖. 21世纪中国极端降水事件预估. 气候变化研究进展, 2007, 3, (4): 202–207.
[12] Phillips T J, Gleckler P J, Evaluation of continental precipitation in 20th century climate simulations: The utility of multimodel statistics. Water Resour Res, 2006, 42: W03202. DOI:10.1029/2005WR004313
[13] Sun Y, Solomon S, Dai A, et al. How often does it rain?. J Climate, 2006, 19: 916–934. DOI:10.1175/JCLI3672.1
[14] Wang H L, Lau K M, Atmospheric hydrological cycle in the tropics in twentieth century coupled climate simulations. Int J Climatol, 2006, 26: 655–678. DOI:10.1002/(ISSN)1097-0088
[15] Cook K H, Vizy E K, Coupled model simulations of the West African monsoon system: 20th century simulations and 21st century predictions. J Climate, 2006, 19: 3681–3703. DOI:10.1175/JCLI3814.1
[16] Wang B, Kang I S, Lee J Y, Ensemble simulation of Asian-Australian monsoon variability by 11 GCMs. J Climate, 2004, 17: 803–818. DOI:10.1175/1520-0442(2004)017<0803:ESOAMV>2.0.CO;2
[17] 赵宗慈, 丁一汇, 李晓东, 等. 海气耦合模式在东亚地区的可靠性评估. 应用气象学报, 1995, 6, (增刊): 9–18.
[18] Iorio J P, Duffy P B, Govindasamy B, et al. Effects of model resolution and subgrid scale physics on the simulation of precipitation in the continental United States. Climate Dyn, 2004, 23: 243–258.
[19] Emori S, Hasegawa A, Suzuki T, et al. Validation, parameterization dependence and future projection of daily precipitation simulated with an atmospheric GCM. Geophys Res Lett, 2005, 32: L060708.
[20] 翟盘茂, 潘晓华. 中国北方近50年温度和降水极端事件变化. 地理学报, 2003, 58, (增刊): 1–10.
[21] Bonsal B R, Zhang X B, Vincent L A, et al. Characteristics of Daily and Extreme temperature over Canada. J Climate, 2001, 5, (14): 1959–1976.
[22] 张莉, 丁一汇, 孙颖. 全球海气耦合模式对东亚季风降水模拟的检验. 大气科学, 2008, 32, (2): 261–276.