太阳辐射是地球气候系统的最终驱动力, 地表短波辐射作为太阳辐射的一个重要分支, 在地表能量平衡中起着重要作用。气候模式能否对地表短波辐射的分布和变化进行合理的模拟, 将直接影响利用气候模式对未来气候变化进行的预估。
大量研究表明, 大气环流模式 (GCMs) 对太阳辐射在地气系统中如何分配的模拟还存在很大的不确定性[1-2]。目前GCMs普遍高估地表入射短波辐射 (平均约9 W/m2), 并在地表短波辐射收支上表现出很大的差异, 这说明不同GCMs在大气吸收短波辐射上还存在很大的不确定性[3]。大气吸收短波辐射3个主要因子中 (云、水汽和气溶胶), 云及其辐射效应是当前气候模式 (CGCMs) 不确定性的主要来源, 而短波云辐射反馈是模式间云反馈差异的主要原因[4]; 水汽对大气短波辐射的吸收通常为GCMs所低估[2, 5-6]; 此外, GCMs普遍对气溶胶处理得较粗, 如果GCMs中不考虑具有强吸收作用的气溶胶将在相应区域产生过多的地表短波入射辐射[7]。在年际变化上, 观测研究表明, 在1990年以前地球经历了一个变暗的过程[8], 20世纪后半段中国地区地表入射短波辐射的减小也十分明显[9-10]。模式能否对这种现象进行模拟十分重要。
我国地处东亚季风区, 受特殊的地理地形条件影响, 我国的辐射和云辐射强迫特征表现出很强的独特性, 并可能和季风气候有密切联系[11-12]。尤其是地表短波辐射直接影响地表的热力状况, 其模拟差异可能对季风模拟产生重要影响。因此, 分析气候模式对东亚地区地表短波辐射的模拟能力十分必要。本文将利用最新的IPCC A R4全球气候模式输出结果, 重点分析模式对东亚地区地表短波辐射的气候平均、季节变化及年际变化特征, 揭示模拟中存在的主要问题, 为进一步改进气候模式在东亚地区的模拟提供科学支持。
1 资料和方法 1.1 模式和资料本文所用到的模式结果来源于WCRP CMIP3多模式数据集 (前身为IPCC AR4模式结果数据库), 该数据集共收集了全球23个耦合模式的模拟结果, 选取具有完整辐射变量输出18个模式用于本文分析。这18个模式分别是:CGCM 3.1(T47)(加拿大), CGCM 3.1(T63)(加拿大), CNRM-CM 3(法国), GFDL-CM 2.0(美国), GFDL-CM 2.1(美国), GISS-EH (美国), GISS-ER (美国), FGOA LS-g 1.0 (中国), INM-CM 3.0(俄罗斯), IPSL-CM 4(法国), MIROC3.2(hire s)(日本), M IROC3.2(medres)(日本), ECH O-G (德国/韩国), ECH AM5/M PI-OM (德国), M RI-CGCM 2.3.2(日本), CCSM 3(美国), UKM O-H adCM3 (英国), UKMO-H adGEM 1 (英国)。有关模式的具体信息可参阅网站:http :∥ www-pcmdi.llnl.gov/ipcc/model documentation/ipcc model documentation.php。
本文用到的是“20世纪气候模拟”(20C3M) 试验月平均输出结果, 变量主要有全天和晴空条件下地表向下和向上短波辐射。模式验证资料采用的是欧洲中心40年月平均再分析资料 (ERA40) 提供的相应辐射资料。资料截取二者共有时段, 即1958年1月-1999年12月, 共42年。
1.2 资料处理方法考虑到不同模式的空间分辨率差别较大, 为便于进行模拟结果的集合以及模拟与观测之间对比, 利用双线性插值方法将不同模式的模拟结果插值到2.5°×2.5°的经纬度网格上。
多模式集合的结果由各模式结果对应时间和空间点求算术平均得到:

|
(1) |
式 (1) 中, N为模式个数, Xi, j, t, m为第m个模式、某格点 (第i个经度、第j个纬度) 处, 第t个时间的值, Xi, j, t, e为对应时间该空间点的多模式集合 (平均) 值。
为考察模拟结果与观测结果之间的差距, 计算了模式的均方根偏差:

|
(2) |
式 (2) 中, xlm为模式模拟的气候平均第l个月的短波辐射, xlobs为观测的气候平均第l个月的短波辐射, n为资料长度, DRMS为均方根偏差。
为表示模式间差异, 计算了不同模式结果之间的标准差:

|
(3) |
式 (3) 中, xm为第m个模式的值, x为18个模式的平均值, STDEV为标准差。
为更好地理解云在地表短波辐射中所起的作用, 将云辐射强迫[13]的概念应用到地表, 以表示云对地表短波辐射的影响, 即地表短波云辐射强迫:

|
(4) |
式 (4) 中, CRF, RS和RSC分别表示地表短波云辐射强迫、全天地表短波辐射和晴空地表短波辐射。
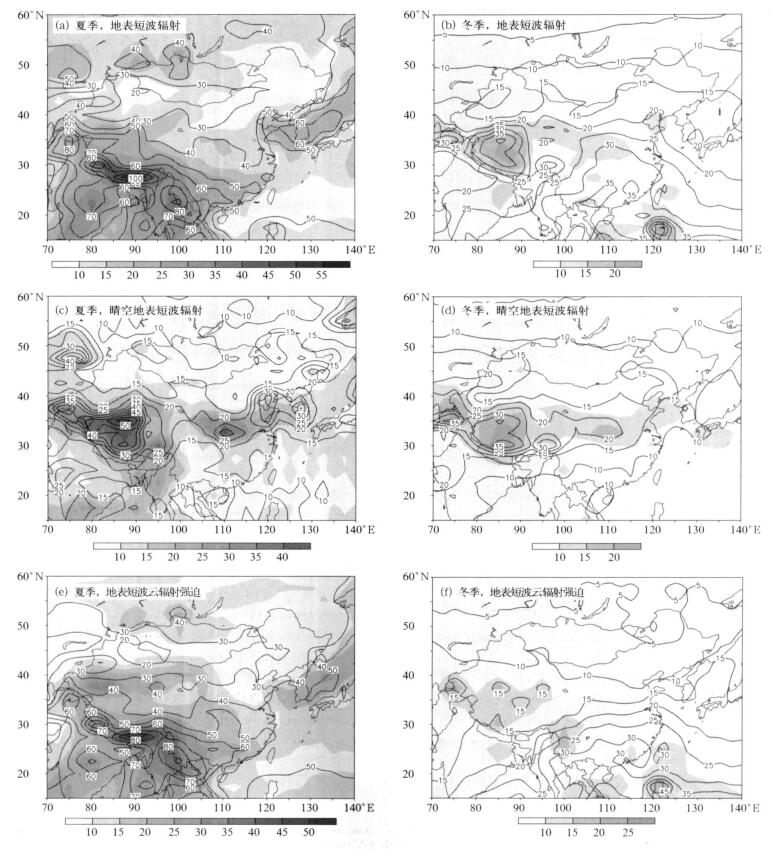
2 结果分析 2.1 平均态的模拟 2.1.1 多模式集合对多年气候平均态的模拟是考察模式性能的基本指标。首先分析ERA40给出的地表短波辐射多年平均分布 (图略)。夏季, 地表短波辐射主要呈现“两高一低”分布。其中一个高值区位于新疆塔里木盆地、准噶尔盆地以及内蒙古中西部, 这是我国云量最少、云层最薄的地区[14], 这导致该地区成为我国夏季地表短波辐射最高的地区 (局部高达240 W/m2以上); 另一个高值区位于我国东部洋面的副热带高压活动区, 海洋较低的反照率和高压控制区多晴朗少云的天气共同导致了该地较高的地表短波辐射。低值区主要位于印度半岛以东到我国江南一带, 这和夏季风期间旺盛的云系活动相联系, 低值中心位于孟加拉湾北部到东部的陆地地区 (也是夏季云量最大的地区, 一般在9成左右), 一般在100 W/m2以下。冬季, 东亚盛行冬季风, 云量明显减少, 地表短波辐射呈明显的纬向分布特征, 并向北逐渐减小。通过和云量分布进行对比发现, 地表短波辐射和云量分布呈显著负相关, 二者空间相关系数夏季和冬季分别为-0.68和-0.59(均通过了0.01的显著性检验), 可见云对地表短波辐射起着十分关键的作用。
图 1a~b分别给出了多模式集合多年平均地表短波辐射相对于ERA40的差值, 从图中可以看出, 夏季, 大陆地区以模拟偏多为主, 尤其在35°N以南的大陆地区, 地表短波辐射模拟得明显偏多, 中心偏高可达80 W/m2, 这主要是由于这些地区是东亚夏季风期间云量最多的地区, 而模式对该地区云量的模拟明显偏低, 导致该地区地表短波云辐射强迫明显偏低 (图 1e), 从而起到了增大地表短波辐射的作用; 而在我国东部洋面到日本海一带, 地表短波辐射模拟偏低, 在这些地区地表短波云辐射强迫模拟偏高, 同时晴空地表短波辐射模拟偏低, 二者对地表短波辐射的贡献相同, 都是降低地表短波辐射, 使得该地区地表短波辐射模拟偏低。冬季, 模拟偏差明显小于夏季, 从青藏高原往东直到日本海附近, 模拟明显偏低, 主要是由于晴空辐射模拟偏低, 同时云辐射强迫模拟偏高, 二者都起到降低地表短波辐射的作用; 而在中亚、南亚到东南亚一带, 模拟明显偏高, 这主要是由于晴空辐射模拟偏高引起的。

|
|
| 图 1. 多模式集合地表短波辐射、睛空地表短波辐射和地表短波云辐射强迫与ERA的差值 (Ensemble-ERA40)(单位:W/m2, 阴影部分表示通过0.01的显著性检验) Fig 1. Difference of surface shortwave radiation (SSR), clear-sky SSR, and surface shortwavw cloud radiative forcing (SSCRF) between multi-model ensemble and ERA40(Ensemble-ERA 40) (unit :W/m2, shaded areas denote passing the test of 0.01 level) | |
夏季地表短波云辐射强迫以偏低为主, 而冬季以偏高为主, 且夏季模拟偏差要明显大于冬季。总的来说, 地表短波云辐射强迫在云量高的地区有模拟偏低的趋势 (如夏季风活动区), 而在云量少的地区有模拟偏强的趋势 (如大陆冬季风控制区和我国夏季西北的少云区)(图 1e~f)。
晴空地表短波辐射的模拟偏差夏季和冬季分布较为一致, 主要表现为青藏高原、我国中部到日本海附近以及冬季的大陆高纬度地区模拟偏低, 而其他地区以偏高为主 (图 1c~d)。晴空地表短波辐射的模拟偏差是多方面原因共同作用的结果:一是地表反照率, 从图 2a~b可以看出, 地表反照率模拟以偏高为主, 在青藏高原和冬季的高纬度地区偏高可达10%以上 (这可能和积雪模拟偏多有关), 这将起到降低地表短波辐射的作用。二是大气对短波辐射的吸收作用, 图 2c~d中的晴空地表入射短波辐射模拟明显偏多, 说明大气对短波辐射的吸收偏弱, 这可能主要是由于水汽和气溶胶的模拟偏差引起的[15]。研究表明, 模式对东亚地区水汽的模拟总体以偏少为主[16], 这部分解释了晴空地表短波辐射模拟偏高的现象; 气溶胶对短波辐射也有着重要影响, 但由于模式总体上对气溶胶的处理较为简单, 只考虑了部分气溶胶 (以硫酸盐气溶胶为主) 的直接辐射效应, 其对地表短波辐射的模拟偏差究竟有多大的贡献, 受资料的限制, 目前还无法给出具体的结论。此外还有一个原因就是辐射算法的差异会造成大气顶入射辐射的明显差异[17], 但这种偏差相对较小且一般呈纬向分布, 不足以解释晴空地表入射短波辐射模拟偏差由海洋指向陆地的纬向梯度分布。

|
|
| 图 2. 多模式集合地表反照率 (单位:%) 和晴空地表入射短波辐射 (单位:W/m2) 与ERA的差值 (Model-ERA40) Fig 2. Difference of surface albedo (unit :%) and clear-sky downscaling shortwave radiation (unit :W/m2) between multi-model ensemble and ERA 40(Ensemble-ERA40) | |
2.1.2 模式间差异
图 3给出了不同模式模拟的区域平均地表短波辐射、晴空地表短波辐射和地表短波云辐射强迫相对ERA40的差值。从图 3可以看出, 模式对地表短波辐射和晴空地表短波辐射模拟以偏高为主, 而云对短波辐射的影响模拟普遍偏弱。18个模式中有14个模拟的地表短波辐射偏高, 偏高最多的是FGOA LS-g 1.0和MIROC3.2(hires), 分别偏高约27 W/m2和23 W/m2。对于晴空地表短波辐射, 有11个模式模拟偏高, 最高的是FGOALS-g1.0, 偏高约20 W/m2。云对短波辐射的作用, 14个模式模拟偏弱, 最弱的是IPSL-CM 4, 偏小约23 W/m2。

|
|
| 图 3. 不同模式模拟的区域平均地表短波辐射、晴空地表短波辐射和地表短波云辐射强迫相对ERA 40的差值 (M odel-ERA40)(单位:W/m2) Fig 3. Regional average difference between simulation and ERA 40 for SSR, clear-sky SSR and SSCRF (Model-ERA40)(unit:W/m2) | |
多模式平均来看, 地表短波辐射偏高约8.7 W/m2, 晴空地表短波辐射偏高约3.4 W/m2, 地表短波云辐射强迫偏低约5.3 W/m2, 代表模式间差异的标准差分别达到9.6, 7.8 W/m2和8 W/m2。
2.2 季节变化图 4给出了多年平均地表短波辐射、晴空地表辐射以及地表短波云辐射强迫的纬向平均季节变化, 可以看出, 晴空地表短波辐射和云辐射强迫基本呈冬低夏高变化, 而地表短波辐射高值区呈倾斜变化, 低纬高值区出现要比高纬早。对这些季节变化的位相特征, 多模式集合都能够很好地进行模拟。地表短波辐射季节变化 (图 4a~b) 主要有两个220 W/m2以上的高值中心, 一个出现在20°N以南的2-5月, 主要是由于热带洋面上 (主要是孟加拉湾) 的异常高值区引起的, 另一个出现在40°N附近的4-8月, 主要和我国西北的少云区和东部洋面的副热带高压控制区相对应。晴空地表短波辐射的变化 (图 4c~d) 较为单一, 主要反映了地球公转引起的入射太阳辐射的季节变化。地表短波云辐射强迫的变化 (图 4e~f) 和亚洲季风的进退紧密联系, 高值区主要出现在35°N以南的5-9月, 云辐射强迫普遍大于100 W/m2, 主要和我国长江流域以南的夏季风活动区相对应。

|
|
| 图 4. ERA 40和多模式集合模拟的地表短波辐射、晴空地表短波辐射和地表短波云辐射强迫的纬向平均季节变化 (等值线) 及其的差值 (Ensemble-E RA40, 阴影)(单位:W/m2) Fig 4. Seasonal variation of zonally averaged SSR, clear-sky SSR and SSCRF for ERA 40 and multi-model ensemble (contour) and their difference (shaded, Ensemble-E RA40)(unit :W/m2) | |
尽管多模式集合能够较好地模拟地表短波辐射的季节变化, 但在量值上还有较大的差距。多模式集合对地表短波辐射的模拟偏差在30°N以南明显偏高, 尤其在夏半年普遍偏高30~50 W/m2, 这主要是由于模式对夏季风活动区的云辐射强迫模拟明显偏低, 低估了该地区云对短波辐射的削弱作用, 同时这些地区的晴空地表短波辐射也被高估, 二者作用相同, 使得该地区出现了最大的模拟偏差。而在30°N以北, 上半年以偏少为主, 主要是云辐射强迫模拟偏强造成的; 下半年云辐射强迫模拟也以偏强为主, 但晴空短波辐射模拟偏高, 二者量级相当但作用相反互相抵消, 使得该地区地表短波辐射模拟偏差较小。
2.3 模拟偏差分析模式模拟的偏差可以从两方面来考虑:一是模式相对于观测的偏差, 这里用均方根偏差来表示; 二是不同模式均方根偏差之间存在的差异, 这里用模式间的标准差表示。图 5分别给出了多模式集合的全天和晴空地表短波辐射、地表短波云辐射强迫的均方根偏差以及不同模式均方根偏差的标准差。总的看来, 均方根偏差夏季明显大于冬季, 尤其地表短波辐射和云辐射强迫更为明显, 这从区域平均的季节变化上也可看出 (图 6)。夏季, 地表短波辐射的均方根偏差 (图 5a~b) 普遍在30 W/m2以上, 最大值中心位于印度北部到中南半岛一带, 可达80 W/m2以上; 冬季均方根偏差明显变小, 大于30 W/m2的地区主要位于35°N以南。从短波云辐射强迫均方根偏差的分布看 (图 5e~f), 其与地表短波辐射均方根偏差分布基本一致 (夏季和冬季的空间相关系数分别达到0.89和0.88), 且量级差别不大, 说明云在地表短波辐射收支中起着主要作用。对于晴空地表短波辐射 (图 5c~d), 均方根偏差最大的地区主要位于青藏高原附近, 可能是由于高原积雪模拟不好造成。
|
|
| 图 5. 地表短波辐射、晴空地表短波辐射和地表短波云辐射强迫的多模式集合均方根偏差 (等值线) 和模式间差异标准差 (阴影)(单位:W/m2) Fig 5. Multi-model ensemble of root mean square deviation (contour) and inter-model standard deviation (shaded) of SSR, clear-sky and SSCRF (unit :W/m2) | |

|
|
| 图 6. 区域平均均方根偏差和标准差的季节变化 (a) 地表短波辐射, (b) 晴空地表短波辐射, (c) 地表短波云辐射强迫, (d) 地表短波云辐射强迫与晴空地表短波辐射的比值 Fig 6. Seasonal variation of regional average of root mean square deviation and standard deviation (a) SSR, (b) clear-sky SSR, (c) SSCRF, (d) ratio of SSCRF to clear-sky SSR | |
对于模式间标准差, 从图 5可以看出, 其与均方根偏差之间呈现较为一致的分布, 即均方根偏差大的地方, 模式间差异 (标准差) 也大, 同时, 二者也有着较为一致的季节变化 (图 6a~c), 这从二者逐月的空间相关系数上可以得到很好的证明, 二者呈显著的正相关关系 (表 1)。为更好地理解云在模拟差异中所起的作用, 给出了短波云辐射强迫和晴空地表短波辐射均方根偏差、标准差之间的比值 (图 6d), 从图中可以看出, 几乎所有月份的比值均大于1, 夏季甚至达到2以上, 说明云对模拟均方根偏差的贡献十分巨大。而对与模式间的标准差, 云在6-10月所起的作用更大, 其余月份晴空条件下的贡献更大。
|
|
表 1 多模式集合均方根偏差和模式间标准差之间的空间相关系数 Table 1 Spandard coef ficients between multi-model ensemble of root mean square devlation and inter-model standard deviation |
多模式集合的区域年平均地表短波辐射、晴空地表短波辐射、地表短波云辐射强迫的均方根偏差分别为34.7, 17.1 W/m2和29.1 W/m2, 说明云在地表短波辐射的模拟偏差中起着重要作用; 而模式间均方根偏差的标准差分别为12.5, 11.3 W/m2和10.2 W/m2, 差距相对较小。
2.4 年际变化特征考察模式对全球变暗的模拟能力。图 7a给出了区域平均地表入射短波辐射的年际变化, 可以看出, ERA40给出的地表入射短波辐射存在明显减小的趋势 (-0.77 W · m-2/10a), 多模式集合能够很好地模拟出这种线性减小趋势, 递减率约为-0.84 W · m-2/10a, 与ERA40给出的十分接近。分别考察晴空和云的作用, 二者变化趋势的模拟并不理想, 对于晴空地表入射短波辐射 (图 7b), 多模式模拟的线性递减率约为-1 W · m-2/10a, 远大于ERA40的-0.16 W ·m-2/ 10a;而对于云入射短波辐射强迫 (图 7c), 模拟呈略有减小的趋势 (-0.16 W ·m-2/10a), 与ERA40的明显增加趋势完全相反 (0.6 W · m-2/10a), 说明模式对云的模拟还存在较大的问题。

|
|
| 图 7. 地表入射短波辐射年际变化 (a) 地表入射短波辐射, (b) 晴空地表入射辐射, (c) 地表短波云辐射强迫, (d) 模式间标准差 Fig 7. Annual variation of surface downscaling shortwave radiation (a), clear-sky surface downscaling shortwave radiation (b), surface shortwave cloud radiative forcing (c) and inter-model standard deviation (d) | |
需要指出, 尽管多模式集合模拟的区域平均地表入射短波辐射的变化趋势与ERA40十分接近, 但在变化趋势的空间分布上, 二者还有较大的差距, 主要表现在模式模拟的线性趋势在整个区域内都是一致减小的, 而ERA40给出的线性趋势在东亚范围内有正有负, 尤其在印度半岛、我国西南部分地区以及日本附近呈现较明显的上升趋势 (图略)。此外, 多模式集合模拟的区域平均地表入射短波辐射明显偏大, 平均偏高14 W/m2左右。分析其中原因, 一方面是由于晴空大气对入射辐射的吸收偏弱, 导致到达地表的短波辐射约偏高9 W/m2; 另一方面是由于云对短波辐射的吸收作用偏弱, 其对地表入射短波辐射偏高的贡献约为5 W/m2。
对于模式间差异 (图 7d), 地表入射短波辐射最大, 约13 W/m2, 云入射短波辐射强迫次之, 约8.7 W/m2, 晴空地表入射短波辐射最小, 约7.4 W/m2。
3 小结和讨论本文利用WCRP CMIP3提供的18个全球气候模式输出结果和ERA40再分析资料, 检验了其对东亚地区地表短波辐射的模拟能力, 得出以下主要结论:
1) 从区域平均来看, 模式间的差异十分明显, 模式对地表短波辐射和晴空地表短波辐射模拟总体以偏高为主, 而云对短波辐射的影响模拟普遍偏弱。多模式集合的多年平均地表短波辐射模拟偏高约8.7 W/m2, 晴空地表短波辐射模拟偏高3.4 W/m2, 地表短波云辐射强迫模拟偏低约5.3 W/m2, 模式间的标准差分别达到9.6, 7.8 W/m2和8 W/m2。在区域分布上, 夏季, 在35°N以南的大陆地区, 地表短波辐射模拟得明显偏多, 而在我国西北北部和我国东部洋面到日本海一带模拟偏低; 冬季, 模拟偏差明显小于夏季, 从青藏高原以东到日本海附近模拟偏低, 而在中亚、南亚到东南亚一带模拟偏高。
2) 多模式集合能够很好地模拟出地表短波辐射的纬向平均季节变化的位相特征, 但在量值上还有较大的差距。在30°N以南模拟明显偏高, 尤其在夏半年普遍偏高30~50 W/m2, 这主要是由于模式对夏季风活动区的云辐射强迫模拟明显偏低, 同时这些地区的晴空地表短波辐射也被高估, 二者作用相同, 使得该地区出现了最大的模拟偏差。而在30°N以北, 上半年以偏少为主, 主要是云辐射强迫的模拟偏强造成的。
3) 模拟偏差分析表明, 模式均方根偏差夏季明显大于冬季。多模式集合的区域年平均地表短波辐射、晴空地表短波辐射、地表短波云辐射强迫的均方根偏差分别为34.7, 17.1 W/m2和29.1 W/m2, 表明云在地表短波辐射的模拟偏差中起着重要作用; 而模式间均方根偏差的标准差分别为12.5, 11.3 W/m2和10.2 W/m2, 差距相对较小。
4) 多模式集合能够很好地模拟出地表入射短波辐射年变化的线性减小趋势, 但对于晴空地表辐射和地表云入射短波辐射强迫, 二者的变化趋势模拟得并不理想, 主要表现为, 模式高估了晴空入射辐射的减小趋势, 而模拟的云辐射强迫的变化趋势与ERA40完全相反。
本文研究表明, 地表短波辐射的模拟偏差与东亚季风期间云及其辐射效应可能存在紧密的联系, 这种模拟偏差究竟会对东亚季风的模拟产生何种影响将有助于进一步认识云辐射相互作用和东亚季风之间的关系, 从而有助于从云辐射角度进一步改进模式对东亚季风的模拟, 有关这方面的工作将有待于进一步研究。
| [1] | Li Z, Moreau L, Arking A, On solar energy disposition. Bull Am Meteorol Soc, 1997, 78: 53–70. DOI:10.1175/1520-0477(1997)078<0053:OSEDAP>2.0.CO;2 |
| [2] | Wild M, Ohmura A, Gilgen H, The disposition of radiative energy in the global climate system: GCM versus observational estimates. Clim Dyn, 1998, 14: 853–869. DOI:10.1007/s003820050260 |
| [3] | Wild M, Solar radiation budgets in atmospheric model intercomparisons from a surface perspective. Geophys Res Lett, 2005, 32: L07704. DOI:10.1029/2005GL022421.850 |
| [4] | IPCC. Climate Change 2007: The Physical Science Basis// Solomon S, Qin D, Manning M, et al. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge: Cambridge University Press, 2007 |
| [5] | Arking A, Absorption of solar energy in the atmosphere:Discrepancy between model and observations. Science, 1996, 273: 779–782. DOI:10.1126/science.273.5276.779 |
| [6] | Wild M, Ohmura A, Gilgen H, et al. Validation of GCM simulated radiative fluxes using surface observations. J Clim, 1995, 8: 1309–1324. DOI:10.1175/1520-0442(1995)008<1309:VOGCMR>2.0.CO;2 |
| [7] | Cusack S, Slingo A A, Edwards J M, et al. The radiative impact of a simple aerosol climatology on the Hadley Centre atmospheric GCM. Q J R Meteorol Soc, 1998, 124: 2517–2526. |
| [8] | Wild M, Gilgen H, Roesch A, et al. From dimming to brightening: Decadal changes in solar radiation at the Earth's surface. Science, 2005, 308: 847–850. DOI:10.1126/science.1103215 |
| [9] | Che H Z, Shi G Y, Zhang X Y, et al. Analysis of 40 years of solar radiation data from China, 1961--2000. Geophys Res Lett, 2005, 32. DOI:10.1029/2004GL022322 |
| [10] | Liang F, Xia X A, Long term trends in solar radiation and the associated climatic factors over China for 1961--2000. Annales Geophysicae, 2005, 2: 2424–2432. |
| [11] | Yu R C, Yu Y Q, Zhang M H, Comparing cloud radiative properties between the Eastern China and the Indian monsoon region. Adv Atmos Sci, 2001, 18, (6): 1090–1102. |
| [12] | Wang W C, Gong W, Kau W S, et al. Characteristics of cloud radiative forcing over east China. J Climate, 2004, 17, (4): 845–853. DOI:10.1175/1520-0442(2004)017<0845:COCRFO>2.0.CO;2 |
| [13] | Ramanathan V, The role of earth radiation budget studies in climate and general circulation research. J Atmos Sci, 1987, 37: 447–454. |
| [14] | 刘洪利, 朱文琴, 宜树华, 等. 中国地区云的气候特征分析. 气象学报, 2003, 61, (4): 466–473. |
| [15] | 尹宏. 大气辐射学基础. 北京: 气象出版社, 1993. |
| [16] | 张莉.全球海气耦合模式对东亚降水模拟的检验.北京:中国科学院研究生院, 2008 |
| [17] | 汪方, 丁一汇, 徐影. 辐射参数化方案对一个海气耦合模式云和辐射模拟的影响. 应用气象学报, 2007, 18, (3): 257–265. |
 2008, 19 (6): 749-759
2008, 19 (6): 749-759


